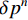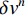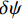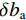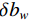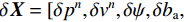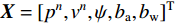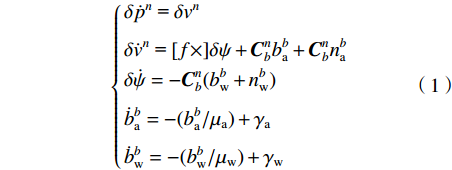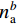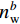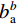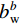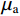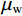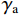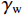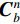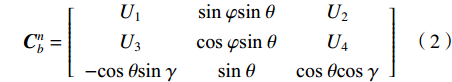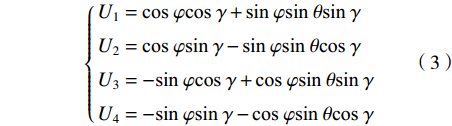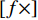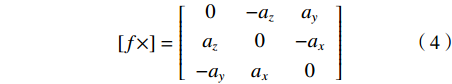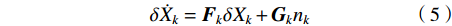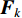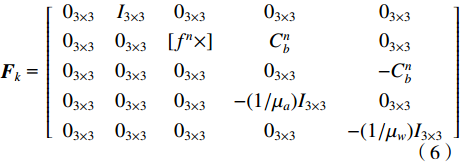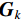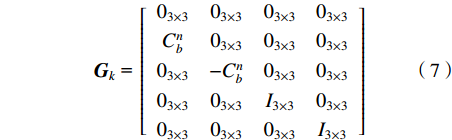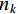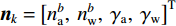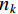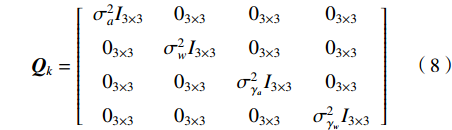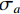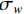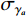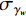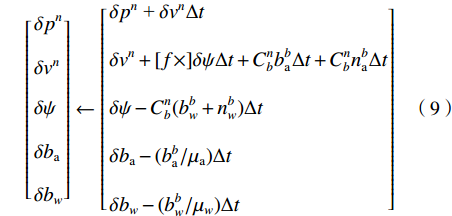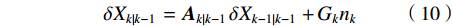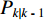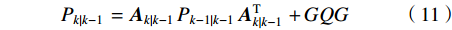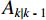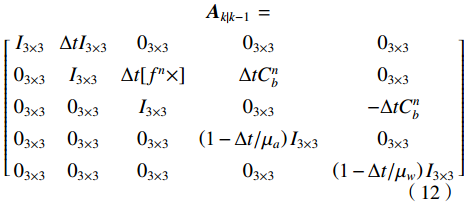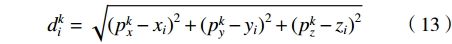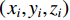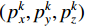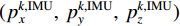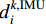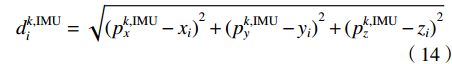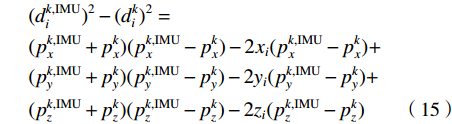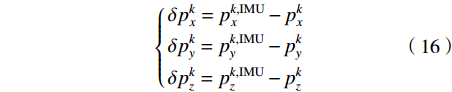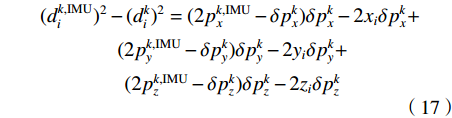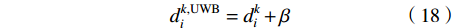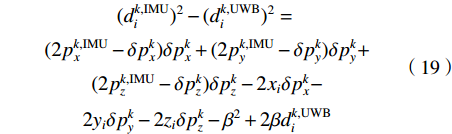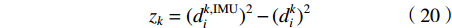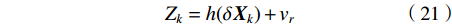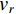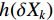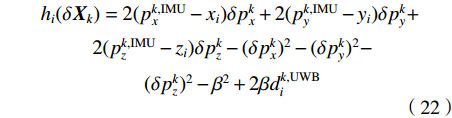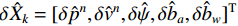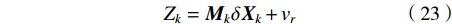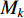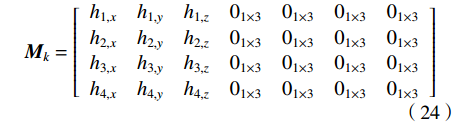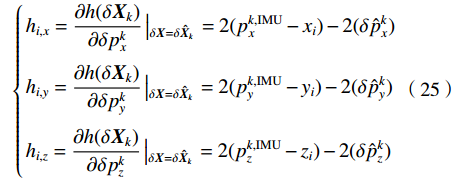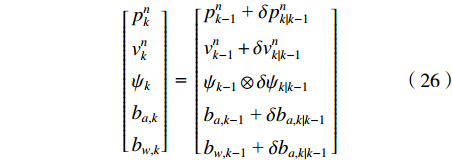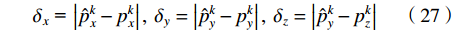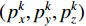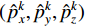Research on shearer positioning experiment based on IMU and UWB at the end of underground coal mining working face
-
摘要:
采煤机自主定位装置的长期精度是采煤工作面智能开采的重要研究内容。针对当前采煤机定位精度难以满足自动开采的需求，建立了基于惯性测量单元(Inertial Measurement Unit, IMU)/超宽带(Ultra-Wideband, UWB)融合定位的模型，提出了采煤工作面端头自主修正补偿惯性导航定位装置的漂移误差，利用IMU/UWB的融合结果对惯性导航定位装置的位置和姿态进行自主纠偏，能实时补偿IMU的偏差，实现采煤机长期高精度自主循环截割。为减小不确定的测量噪声对定位结果的影响，提出了利用变分无迹卡尔曼滤波(Variational Bayesian unscented Kalman filter, VB-UKF)技术对定位结果进行平滑处理，进一步提升融合定位精度，在太原重型机械有限公司开展了地面采煤机融合定位试验和山东能源集团济三工作面端头开展井下采煤机机载试验，验证采煤工作面端头的定位精度。试验结果表明，IMU/UWB融合定位精度高于单纯的UWB解算的精度；经过VB-UKF算法平滑后，井下试验的IMU/UWB融合定位的x轴和z轴方向的平均误差分别从0.102 m和0.194 m降低为0.082 m和0.158 m，平均精度对应的提升了19.6%和18.6%；3个姿态角的误差小于2°，在融合定位模型中利用误差扩展卡尔曼滤波实时补偿修正IMU的偏差，能有效的抑制IMU姿态角的漂移，井下现场试验证明了采煤工作面端头定位方法的有效性，为井下IMU/UWB融合定位的应用提供较好的参考和经验。
Abstract:The long-term precision of shearer independent positioning device is an important research content of intelligent mining. The current shearer positioning accuracy is hard to meet the demands of automatic mining, and we established a fusion positioning model based on IMU/UWB, and proposed autonomous correction to compensate the drift error of inertial navigation device for the coal mine working face by using the fusion results of IMU/UWB to correct the position and posture of inertial positioning system. It can compensate the deviation of IMU in real time, and realize long-term high-precision autonomous cycle cutting of the shearer. To reduce the influence of uncertain measurement noise on the positioning results, we use variational Bayesian unscented Kalman filter (VB-UKF) technique to smooth the positioning results in order to further improve the fusion positioning accuracy. To verify the positioning accuracy of the mining face end, fusion positioning experiments are conducted in Taiyuan Heavy Machinery Co., Ltd on the ground and Shandong Energy Group coal mine working face in the underground, respectively. The experimental results demonstrate that, the accuracy of IMU/UWB fusion positioning is higher than that of the single UWB solution. After smoothing via the VB-UKF algorithm, the error in the x-axis and z-axis orientation of the IMU/UWB fusion localization for underground experiments decreased from 0.0102 m and 0.194 m to 0.082 m and 0.158 m, respectively, and the corresponding average accuracy improved by 19.6% and 18.6%. The error of the three pose angles is less than 2°, because the error extended Kalman filter compensates and modifies the IMU bias in the fusion localization model, which can effectively suppress the drift of the IMU posture angle. The underground field experiment proves the effectiveness of the positioning method of coal mining face end, which provides better reference and experience for the further application in underground coalmine by using IMU/UWB fusion positioning.
-
Keywords:
- shearer /
- coal mining working face /
- end positioning /
- Ultra-Wideband /
- IMU
-
0. 引 言
煤矿智能化无人开采是煤炭开采技术变革的方向，是煤矿实现安全高效生产的核心技术[1 ]，是国际煤炭开采领域共同追求的前沿技术，也是实现我国煤矿安全、高效开采的技术跨越[2]。近年来，基于惯性导航系统的采煤机定位技术广泛应用于煤矿企业[3]，但是仍然面临由于惯性元件漂移引起的定位精度低的问题，无法长期为采煤机提供较高的定位精度。SHIFFBAUER [4-5]利用Honeywell的惯性导航系统开发了连采机定位系统。REID[6]和RALSTON [7]提出了闭合路径的方法对定位精度进行优化。方秋实[8]、樊启高[9]、张博渊等[10]、郝尚清等[11]为了实现惯性导航系统的长期定位，在定位精度和误差补偿方面开展了大量研究，但是定位误差仍然偏大，距离采煤机自主导航定位的要求相差甚远。
超宽带（Ultra-Wideband，UWB）技术具有测距精度高、穿透力强、抗干扰性好等优点，可达到厘米级的距离分辨。近年来，不同学者提出将惯性测量单元(Inertial Measurement Unit, IMU)与UWB进行融合定位。HOL[12]提出了一种基于UWB系统和IMU系统融合定位方法，同时实现位置和方向估计，结果表明，即使在多路径和非视距条件下，该融合方法也能获得较好的定位精度。WEN[13]提出了一种基于四元数卡尔曼滤波的IMU和UWB紧耦合导航定位方法，该方法不涉及任何复杂线性化，降低了系统计算复杂度，结果表明，该融合方法在室内的定位精度能够达到厘米级，方向误差在0.066°以内。GIOVANNI[14]和WANG[15]提出了基于IMU与UWB紧融合定位方法，并证明了融合系统的定位精度高于单纯UWB系统的精度。
张斌飞[16]和朱建斌[17]通过扩展卡尔曼滤波算法融合UWB和IMU测量信息，加速度计偏差校正速度和位置，陀螺仪偏差校正四元数，提高了动态定位精度。匡兵[18]提出了一种利用改进的粒子滤波算法实现 UWB与IMU的融合定位，提升了目标节点的定位精度。王春琦[19]提出了基于无迹卡尔曼滤波的IMU和 UWB融合定位算法，仿真试验表明定融合定位算法能有效的提高定位精度和系统的稳定性。
为了将IMU/UWB融合方法应用于采煤机定位，YANG[20]提出采用自适应模糊卡尔曼滤波技术对IMU/UWB导航数据进行融合，利用采煤机模拟试验验证了该方法的有效性。CUI[21]研究了井下UWB与IMU融合定位，提出利用里程计和UWB辅助IMU的定位方法，并构建了18维误差扩展卡尔曼滤波(Extended Kalman filter, EKF)定位模型，在模拟巷道中开展融合定位试验，试验结果表明该融合方法能有效的提升系统的定位精度。LI[22]利用误差状态卡尔曼滤波器集成了IMU系统和UWB系统，实现IMU与UWB的紧融合定位策略，并在模拟巷道中开展定位试验，平均定位误差在0.56 m左右，定位精度较低。FAN[23]提出将UWB基站安装在液压支架上，通过UWB系统获得采煤机的位置实现对惯性导航的误差进行补偿。SONG[24]提出了一种基于优化因子图的UWB/IMU紧耦合的导航定位方法，优化因子图利用历史数据来构造约束条件，并通过求解非线性优化解得到最优状态估计，从而提高融合模型的定位精度，平均定位精度在0.34 m左右。许晓伟等[25]提出了基于UWB/IMU/里程计融合的采煤机端头定位方法，构建了约束方程和因子图优化模型，仿真试验的定位精度在0.15 m左右，虽然基于因子图的融合定位方法具有较好的定位效果，但是因子图的优化计算非常耗时，不利于实时快速的获得定位结果。尽管上述学者提出了将IMU与UWB进行融合，并通过理论分析及模拟试验验证了该融合定位方法的有效性，但是缺少井下环境的试验验证。
借鉴IMU/UWB融合定位的思想，提出了一种能实现采煤机长期自主导航定位的方法，构建了基于误差状态的IMU/UWB融合定位模型，在太原重型机械有限公司和山东能源集团济三采煤工作面端头开展了采煤机机载试验，利用变分无迹卡尔曼滤波(Variational Bayesian unscented Kalman filter, VB-UKF)对定位结果进行平滑处理，进一步提升了IMU/UWB融合定位的估计精度。
1. 端头定位原理
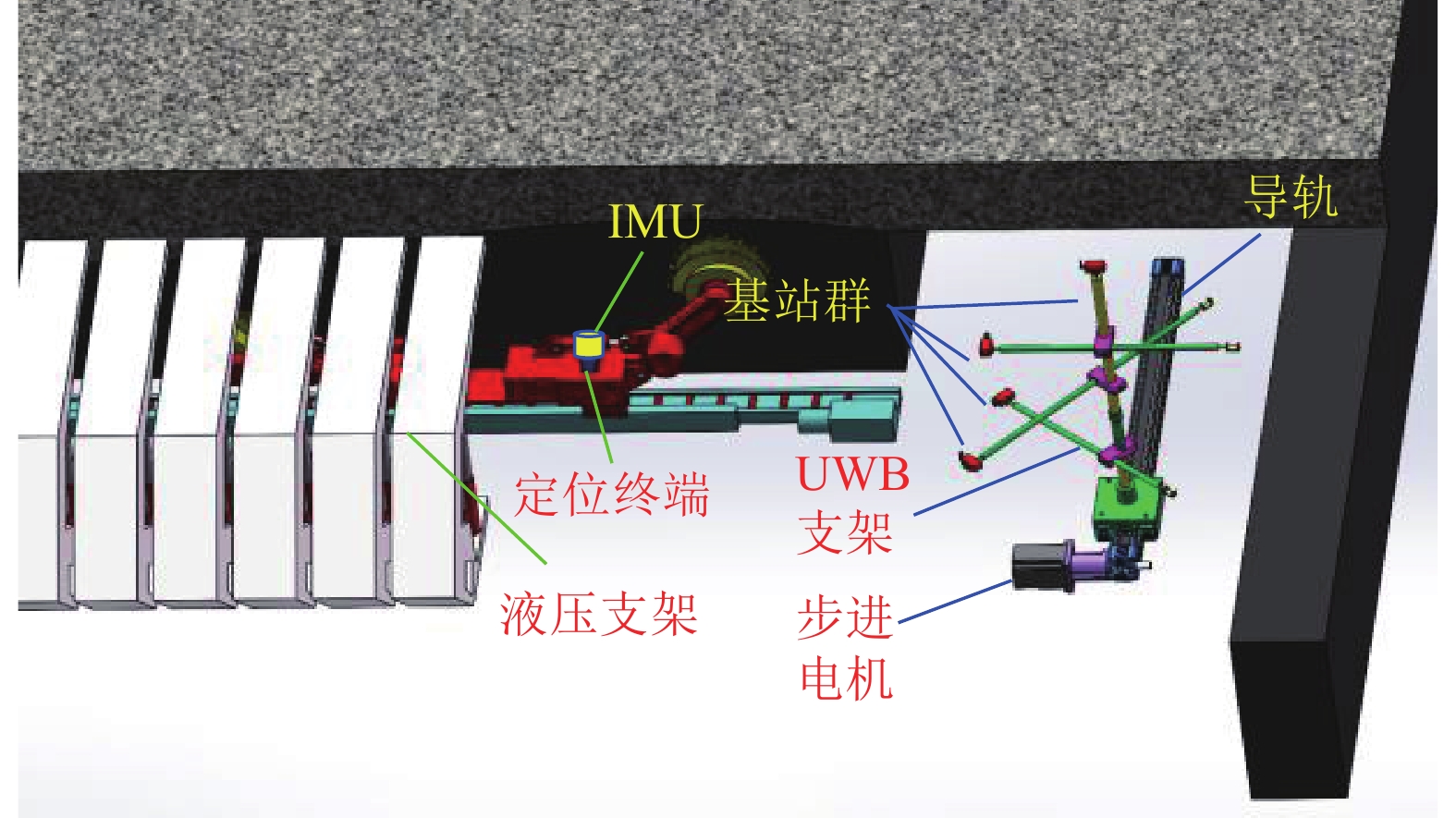
为了使采煤机上的惯性导航装置获得长期的自主导航定位精度，需要对惯性导航的漂移误差进行补偿和修正。为了实现满足采煤机进行长期自主导航定位的需求，提出利用UWB和IMU融合定位方法对惯性导航装置进行端头自主校准，图1给出了采煤工作面端头采煤机IMU/UWB融合定位的原理图。将UWB基站群布局在采煤工作面端头的自主迁移装置上，该迁移装置能使UWB基站群沿着巷道整体移动。当采煤机作业到UWB定位系统的最佳定位范围内时(10 m左右)，同时启动IMU和UWB定位系统，利用IMU/UWB融合定位的结果，对惯性导航系统的位姿偏差进行修正补偿。当采煤机完全截割到机头位置时，惯性导航的位置和姿态得到自主校正，能有效的避免停机后人工校准采煤机的步骤。步进电机控制基站群进行整体迁移，利用上位机中的数据处理单元快速解算出迁移后基站的位置坐标，并将坐标数据传输给UWB系统，为下一次采煤工作面端头采煤机位姿自主校准做好准备，该方法能实现惯性导航定位装置的长期自主导航。
![]()
图 1 采煤工作面端头采煤机自主定位系统结构Figure 1. Structure of the shearer autonomous positioning system of the coal mining face end2. IMU/UWB融合定位方法
在IMU与UWB进行融合定位时，直接利用导航的状态量进行融合，将产生较大的定位误差，往往不是直接利用状态量进行导航定位，而是对状态量的误差进行建模，以位置误差
$ \delta {p^n} $ 、速度误差$ \delta {v^n} $ 、姿态误差$ \delta \psi $ 、加速度计偏差$\delta {b_{\rm{a}}}$ 和陀螺仪偏差$ \delta {b_w} $ 作为融合定位的实际状态量，即$\delta {\boldsymbol{X}} = {[\delta {p^n},\delta {v^n}, \delta \psi ,\delta {b_{\rm{a}}},} \delta {b_{\rm{w}}}]^{\rm{T}}$ ，将${\boldsymbol{X}} = {[{p^n},{v^n},\psi ,{b_{\rm{a}}},{b_{\rm{w}}}]^{\rm{T}}}$ 作为融合系统的名义状态量，则系统误差状态量的微分方程[26]为：$$ \left\{ \begin{gathered} \delta {{\dot p}^n}{\text{ = }}\delta {v^n} \\ \delta {{\dot v}^n}{\text{ = [}}f \times ]\delta \psi + {\boldsymbol{C}}_b^nb_{\rm{a}}^b + {\boldsymbol{C}}_b^nn_{\rm{a}}^b \\ \delta \dot \psi = - {\boldsymbol{C}}_b^n(b_{\rm{w}}^b + n_{\rm{w}}^b) \\ \dot b_{\rm{a}}^b = - (b_{\rm{a}}^b/{\mu _{\rm{a}}}) + {\gamma _{\rm{a}}} \\ \dot b_{\rm{w}}^b = - (b_{\rm{w}}^b/{\mu _{\rm{w}}}) + {\gamma _{\rm{w}}} \\ \end{gathered} \right. $$ (1) 式中：
$n_{\rm{a}}^b$ 和$n_{\rm{w}}^b$ 为均值为0的高斯噪声；$b_{\rm{a}}^b$ 和$b_{\rm{w}}^b$ 分别为加速度计与陀螺仪的时变漂移偏差；${\mu _{\rm{a}}}$ 和${\mu _{\rm{w}}}$ 为时间常数；${\gamma _{\rm{a}}}$ 和${\gamma _{\rm{w}}}$ 为均值为零的白噪声干扰；${\boldsymbol{C}}_b^n$ 为载体坐标系到导航坐标的姿态转换矩阵，如下：$$ {\boldsymbol{C}}_b^n = \left[ {\begin{array}{*{20}{c}} {U_1}&\sin \;\varphi \sin\; \theta &{U_2} \\ {U_3}&\cos \;\varphi \sin \;\theta &{U_4} \\ - \cos\; \theta \sin \;\gamma &\sin\;\theta &\cos \;\theta \cos \;\gamma\\ \end{array}} \right] $$ (2) 其中：
$$ \left\{ \begin{gathered} {U_1} = \cos\; \varphi \cos\; \gamma + \sin\; \varphi \sin \;\theta \sin\; \gamma \\ {U_2} = \cos\; \varphi \sin \;\gamma - \sin \;\varphi \sin\; \theta \cos\; \gamma \\ {U_3} = - \sin\;\varphi \cos \;\gamma + \cos \;\varphi \sin \;\theta \sin\; \gamma \\ {U_4} = - \sin\;\varphi \sin\; \gamma - \cos \;\varphi \sin \;\theta \cos \;\gamma \\ \end{gathered} \right. $$ (3) 式中，φ为航向角；θ为俯仰角；γ为横滚角。
$ {\text{[}}f \times ] $ 代表向量f的反对称矩阵形式，如下：$$ [f \times ]=\left[ {\begin{array}{*{20}{c}} 0& - {a_z}&{a_y} \\ {a_z}&0& - {a_x} \\ - {a_y}&{a_x}&0 \\ \end{array}} \right] $$ (4) 将式(1)进一步转换为如下矩阵形式：
$$ \delta {\dot X_k} = {{\boldsymbol{F}}_k}\delta {X_k} + {{\boldsymbol{G}}_k}{n_k} $$ (5) 其中，
${{\boldsymbol{F}}_k}$ 为状态转移矩阵：$$ {{\boldsymbol{F}}_k}{\text{ = }}\left[ {\begin{array}{*{20}{c}} {0_{3 \times 3}}&{I_{3 \times 3}}&{0_{3 \times 3}}&{0_{3 \times 3}}&{0_{3 \times 3}} \\ {0_{3 \times 3}}&{0_{3 \times 3}}&[{f^n} \times ]&C_b^n&{0_{3 \times 3}} \\ {0_{3 \times 3}}&{0_{3 \times 3}}&{0_{3 \times 3}}&{0_{3 \times 3}}& - C_b^n \\ {0_{3 \times 3}}&{0_{3 \times 3}}&{0_{3 \times 3}}& - (1/{\mu _a}){I_{3 \times 3}}&{0_{3 \times 3}} \\ {0_{3 \times 3}}&{0_{3 \times 3}}&{0_{3 \times 3}}&{0_{3 \times 3}}& - (1/{\mu _w}){I_{3 \times 3}} \\ \end{array}} \right] $$ (6) ${{\boldsymbol{G}}_k}$ 为控制矩阵：$$ {{\boldsymbol{G}}_k}{\text{ = }}\left[ {\begin{array}{*{20}{c}} {0_{3 \times 3}}&{0_{3 \times 3}}&{0_{3 \times 3}}&{0_{3 \times 3}} \\ C_b^n&{0_{3 \times 3}}&{0_{3 \times 3}}&{0_{3 \times 3}} \\ {0_{3 \times 3}}& - C_b^n&{0_{3 \times 3}}&{0_{3 \times 3}} \\ {0_{3 \times 3}}&{0_{3 \times 3}}&{I_{3 \times 3}}&{0_{3 \times 3}} \\ {0_{3 \times 3}}&{0_{3 \times 3}}&{0_{3 \times 3}}&{I_{3 \times 3}} \\ \end{array}} \right] $$ (7) $ {n_k} $ 为扰动矩阵：${{\boldsymbol{n}}_k} = {\left[ {n_{\rm{a}}^b,{\text{ }}n_{\rm{w}}^b,{\text{ }}{\gamma _{\rm{a}}},{\text{ }}{\gamma _{\rm{w}}}} \right]^{\rm{T}}}$ 同时，
$ {n_k} $ 的协方差可用下式表示：$$ {{\boldsymbol{Q}}_k}=\left[ {\begin{array}{*{20}{c}} \sigma _a^2{I_{3 \times 3}}&{0_{3 \times 3}}&{0_{3 \times 3}}&{0_{3 \times 3}} \\ {0_{3 \times 3}}&\sigma _w^2{I_{3 \times 3}}&{0_{3 \times 3}}&{0_{3 \times 3}} \\ {0_{3 \times 3}}&{0_{3 \times 3}}&\sigma _{{\gamma _a}}^2{I_{3 \times 3}}&{0_{3 \times 3}} \\ {0_{3 \times 3}}&{0_{3 \times 3}}&{0_{3 \times 3}}&\sigma _{{\gamma _w}}^2{I_{3 \times 3}} \\ \end{array}} \right] $$ (8) 式中,
$ {\sigma _a} $ 为加速度计测量噪声；$ {\sigma _w} $ 为陀螺仪测量噪声；$ {\text{ }}{\sigma _{{\gamma _a}}} $ 为陀螺仪随机游走噪声；$ {\sigma _{{\gamma _w}}} $ 为加速度计随机游走噪声。根据文献[27]，在IMU系统的2个时间间隔上采用欧拉数值积分获得离散系统的误差状态传递，如下：
$$ \left[ \begin{gathered} \delta {p^n} \\ \delta {v^n} \\ \delta \psi \\ \delta {b_{\rm{a}}} \\ \delta {b_w} \\ \end{gathered} \right] \leftarrow \left[ \begin{gathered} \delta {p^n}{\text{ + }}\delta {v^n}\Delta t \\ \delta {v^n} + [f \times ]\delta \psi \Delta t + C_b^nb_{\rm{a}}^b\Delta t + C_b^nn_{\rm{a}}^b\Delta t \\ \delta \psi - C_b^n(b_w^b + n_w^b)\Delta t \\ \delta {b_{\rm{a}}} - (b_{\rm{a}}^b/{\mu _{\rm{a}}})\Delta t \\ \delta {b_w} - (b_w^b/{\mu _w})\Delta t \\ \end{gathered} \right] $$ (9) 式(9)进一步转换成如下形式：
$$ \delta {X_{k\left| {k-1} \right.}} = {{\boldsymbol{A}}_{k\left| {k-1} \right.}}\delta {X_{k - 1\left| {k - 1} \right.}} + {G_k}{n_k} $$ (10) 则对应的协方差
$ {P_{k\left| {k{\text{ - }}1} \right.}} $ 为：$$ {P_{k\left| {k-1} \right.}} = {{\boldsymbol{A}}_{k\left| {k-1} \right.}}{P_{k-1\left| {k-1} \right.}}{\boldsymbol{A}}_{k\left| {k-1} \right.}^{\rm{T}} + GQG $$ (11) 式中
$ {A_{k\left| {k{\text{ - }}1} \right.}} $ 为误差状态转移矩阵，计算如下：$$ {\begin{array}{*{20}{c}} {{\boldsymbol{A}}_{k\left| {k-1} \right.}}= \\ \left[ {\begin{array}{*{20}{c}} {I_{3 \times 3}} & \Delta t{I_{3 \times 3}} & {0_{3 \times 3}} & {0_{3 \times 3}} & {0_{3 \times 3}} \\ {0_{3 \times 3}} & {I_{3 \times 3}} & \Delta t[{f^n} \times ] & \Delta tC_b^n & {0_{3 \times 3}} \\ {0_{3 \times 3}} & {0_{3 \times 3}} & {I_{3 \times 3}} & {0_{3 \times 3}} & - \Delta tC_b^n \\ {0_{3 \times 3}} & {0_{3 \times 3}} & {0_{3 \times 3}} & \left( {{\text{1}} - \Delta t/{\mu _a}} \right){I_{3 \times 3}} & {0_{3 \times 3}} \\ {0_{3 \times 3}} & {0_{3 \times 3}} & {0_{3 \times 3}} & {0_{3 \times 3}} & \left( {{\text{1}} - \Delta t/{\mu _w}} \right){I_{3 \times 3}} \\ \end{array}} \right]\end{array}} $$ (12) 在UWB系统中，在k时刻，第i个基站与定位终端之间的理论距离为：
$$ d_i^k = \sqrt {{{(p_x^k - {x_i})}^2} + {{(p_y^k - {y_i})}^2} + {{(p_z^k - {z_i})}^2}} $$ (13) 其中，
$ ({x_i},{y_i},{z_i}) $ 为UWB系统中基站的位置坐标， i=1,2,3,4。在k时刻，假设定位终端的真实位置坐标为$ (p_x^k,p_y^k,p_z^k) $ ，IMU系统求解定位终端的位置坐标为$ (p_x^{k,{\rm{IMU}}},{\text{ }}p_y^{k,{\rm{IMU}}},{\text{ }}p_z^{k,{\rm{IMU}}}) $ ，则IMU系统求解定位终端的坐标与第i个基站之间的距离$ d_i^{k,{\rm{IMU}}} $ 可以表示为：$$ d_i^{k,{\rm{IMU}}} = \sqrt {{{(p_x^{k,{\rm{IMU}}} - {x_i})}^2} + {{(p_y^{k,{\rm{IMU}}} - {y_i})}^2} + {{(p_z^{k,{\rm{IMU}}} - {z_i})}^2}} $$ (14) 将式(13)和式(14)两边分别平方，然后两式相减，进行展开整理，则有：
$$ \begin{split} &{(d_i^{k,{\rm{IMU}}})^2} - {(d_i^k)^2} = \\ & (p_x^{k,{\rm{IMU}}} + p_x^k)(p_x^{k,{\rm{IMU}}} - p_x^k) - 2{x_i}(p_x^{k,{\rm{IMU}}} - p_x^k) + \\ & (p_y^{k,{\rm{IMU}}} + p_y^k)(p_y^{k,{\rm{IMU}}} - p_y^k) - 2{y_i}(p_y^{k,{\rm{IMU}}} - p_y^k) + \\ &(p_z^{k,{\rm{IMU}}} + p_z^k)(p_z^{k,{\rm{IMU}}} - p_z^k) - 2{z_i}(p_z^{k,{\rm{IMU}}} - p_z^k) \end{split} $$ (15) 令IMU系统解算的3个坐标轴方向上的误差为
$$ \left\{ \begin{gathered} \delta p_x^k = p_x^{k,{\rm{IMU}}} - p_x^k \\ \delta p_y^k = p_y^{k,{\rm{IMU}}} - p_y^k \\ \delta p_z^k = p_z^{k,{\rm{IMU}}} - p_z^k \\ \end{gathered} \right. $$ (16) 进一步将式(16)代入式(15)，进行整理，则有：
$$ \begin{array}{c} {(d_i^{k,{\rm{IMU}}})^2} - {(d_i^k)^2} = (2p_x^{k,{\rm{IMU}}} - \delta p_x^k)\delta p_x^k - 2{x_i}\delta p_x^k + \\ {\text{ }} (2p_y^{k,{\rm{IMU}}} - \delta p_y^k)\delta p_y^k - 2{y_i}\delta p_y^k + \\ {\text{ }} (2p_z^{k,{\rm{IMU}}} - \delta p_z^k)\delta p_z^k - 2{z_i}\delta p_z^k \end{array}$$ (17) 在UWB定位系统中，第i个UWB基站与定位终端之间实际测量距离表示为如下形式：
$$ d_i^{k,{\rm{UWB}}} = d_i^k + \beta $$ (18) 其中，β为测距误差，将式(18)代入式(17)中进行整理合并，则有：
$$ \begin{array}{c} {(d_i^{k,{\rm{IMU}}})^2} - {(d_i^{k,{\rm{UWB}}})^2}= \\ {\text{ }} (2p_x^{k,{\rm{IMU}}} - \delta p_x^k)\delta p_x^k + (2p_y^{k,{\rm{IMU}}} - \delta p_y^k)\delta p_y^k + \\ {\text{ }} (2p_z^{k,{\rm{IMU}}} - \delta p_z^k)\delta p_z^k - 2{x_i}\delta p_x^k - \\ {\text{ }} 2{y_i}\delta p_y^k - 2{z_i}\delta p_z^k - {\beta ^2} + 2\beta d_i^{k,{\rm{UWB}}} \end{array} $$ (19) 通常情况下，在融合模型中选择IMU系统解算的位置坐标与基站之间的距离减去UWB系统测量距离的差值作为观测量。为了计算方便，对两个距离先平方然后在相减，则融合定位的观测量构建为
$$ {z_k} = {(d_i^{k,{\rm{IMU}}})^2} - {(d_i^k)^2} $$ (20) IMU/UWB融合定位的观测方程表示为
$$ {Z_k} = h(\delta {{\boldsymbol{X}}_k}) + {v_r} $$ (21) 式中，
$ {v_r} $ 为测量噪声，$ h(\delta {X_k}) $ 的计算公式如下：$$ \begin{array}{c} {h_i}(\delta {{\boldsymbol{X}}_k}) = 2(p_x^{k,{\rm{IMU}}} - {x_i})\delta p_x^k + 2(p_y^{k,{\rm{IMU}}} - {y_i})\delta p_y^k + \\ {\text{ }} 2(p_z^{k,{\rm{IMU}}} - {z_i})\delta p_z^k - {(\delta p_x^k)^2} - {(\delta p_y^k)^2}- \\ {\text{ }} {(\delta p_z^k)^2} - {\beta ^2} + 2\beta d_i^{k,{\rm{UWB}}} \end{array} $$ (22) 将式(22)在
$\delta {\hat X_k} = {[\delta {\hat p^n},\delta {\hat v^n},\delta \hat \psi ,\delta {\hat b_a},\delta {\hat b_w}]^{\rm{T}}}$ 处进行泰勒展开，并且只保留一阶泰勒展开项，则量测模型为$$ {Z_k} = {{\boldsymbol{M}}_k}\delta {{\boldsymbol{X}}_k} + {v_r} $$ (23) 式中
$ {M_k} $ 为量测矩阵，其具体形式如下：$$ {{\boldsymbol{M}}_k} = \left[ {\begin{array}{*{20}{c}} {h_{1,x}}&{h_{1,y}}&{h_{1,z}}&{0_{1 \times 3}}&{0_{1 \times 3}}&{0_{1 \times 3}}&{0_{1 \times 3}} \\ {h_{2,x}}&{h_{2,y}}&{h_{2,z}}&{0_{1 \times 3}}&{0_{1 \times 3}}&{0_{1 \times 3}}&{0_{1 \times 3}} \\ {h_{3,x}}&{h_{3,y}}&{h_{3,z}}&{0_{1 \times 3}}&{0_{1 \times 3}}&{0_{1 \times 3}}&{0_{1 \times 3}} \\ {h_{4,x}}&{h_{4,y}}&{h_{4,z}}&{0_{1 \times 3}}&{0_{1 \times 3}}&{0_{1 \times 3}}&{0_{1 \times 3}} \end{array}} \right]$$ (24) 式(24)中的参数计算，如下：
$$ \left\{ \begin{gathered} {h_{i,x}} = \frac{{\partial h(\delta {{\boldsymbol{X}}_k})}}{{\partial \delta p_{x}^k}}\left| {_{\delta {\boldsymbol{X}} = \delta {{\boldsymbol{\hat {X}}}_k}}} \right. = 2(p_x^{k,{\rm{IMU}}} - {x_i}) - 2(\delta \hat p_x^k) \\ {h_{i,y}} = \frac{{\partial h(\delta {{\boldsymbol{X}}_k})}}{{\partial \delta p_y^k}}\left| {_{\delta {\boldsymbol{X}} = \delta {{\boldsymbol{\hat {X}}}_k}}} \right. = 2(p_y^{k,{\rm{IMU}}} - {y_i}) - 2(\delta \hat p_y^k) \\ {h_{i,z}} = \frac{{\partial h(\delta {{\boldsymbol{X}}_k})}}{{\partial \delta p_z^k}}\left| {_{\delta {\boldsymbol{X}} = \delta {{{\boldsymbol{\hat X}}}_k}}} \right. = 2(p_z^{k,{\rm{IMU}}} - {z_i}) - 2(\delta \hat p_z^k) \\ \end{gathered} \right. $$ (25) 式中，i为基站的编号，i=1,2,3,4。
此时，将非线性量测进行局部线性化后，根据状态方程和量测模型，通过卡尔曼滤波对误差状态量和量测量进行更新获得定位终端的导航误差信息，并将更新后误差状态信息反馈到IMU系统，实现在线校正补偿IMU系统的偏差，能够提高采煤工作面端头采煤机融合定位系统的精度。
在IMU/UWB融合系统中，需要估计出融合模型的导航状态和误差状态，误差项和导航状态量的误差在没有任何约束的情况下，定位误差将会一直增大，为了避免这种状况，在将误差状态反馈给IMU系统之前，需要将误差状态量中的位置误差、速度误差、姿态误差设置都设置为0，完成误差状态更新后，需要将误差状态融合到导航状态量中，进入下一时刻的预测和更新。误差状态反馈到IMU系统的过程如下：
$$ \left[ \begin{gathered} p_k^n \\ v_k^n \\ {\psi _k} \\ {b_{a,k}} \\ {b_{w,k}} \\ \end{gathered} \right]{\text{ = }}\left[ \begin{gathered} p_{k - 1}^n{\text{ + }}\delta p_{k\left| {k - 1} \right.}^n \\ v_{k - 1}^n + \delta v_{k\left| {k - 1} \right.}^n \\ {\psi _{k - 1}} \otimes \delta {\psi _{k\left| {k - 1} \right.}} \\ {b_{a,k - 1}}{\text{ + }}\delta {b_{a,k\left| {k - 1} \right.}} \\ {b_{w,k - 1}}{\text{ + }}\delta {b_{a,k\left| {k - 1} \right.}} \\ \end{gathered} \right] $$ (26) 考虑到时变未知测量噪声对定位精度的影响，利用VB-UKF自适应滤波算法对纯UWB定位结果和IMU/UWB松融合定位结果进行平滑处理，进一步提升定位结果的估计精度，VB-UKF算法的具体执行过程可查询文献[28]。
在试验过程中，采煤机沿着y轴的方向作直线运动，定位终端在x轴和z轴方向的坐标不变，可以计算出x轴和z轴方向的误差，由于缺乏y方向上的真实值，无法直接计算y轴方向的误差。采用坐标轴方向的绝对误差作为主要评价指标，如下：
$$ {\delta _x}{\text{ = }}\left| {\hat p_x^k - p_x^k} \right|,{\text{ }}{\delta _y} = \left| {\hat p_y^k - p_y^k} \right|,{\text{ }}{\delta _z} = \left| {\hat p_y^k - p_z^k} \right| $$ (27) 式中：
$ (p_x^k,p_y^k,p_z^k) $ 为定位终端的真实坐标；$ (\hat p_x^k,\hat p_y^k,\hat p_z^k) $ 为定位算法求解的坐标。3. 试验结果与分析
为评价基于误差卡尔曼滤波的IMU/UWB融融合定位方法的有效性，在太原重型机械有限公司的矿山采掘装备及智能制造国家重点实验室开展了地面采煤融合定位试验，是为探究采煤机运动过程中融合定位方法的定位精度变化情况。为进一步将IMU/UWB融合定位方法应用于井下实际定位环境中，考察UWB定位系统受到井下采煤机的震动、煤粉和水雾的干扰时定位精度变化情况，同时评估融合定位方法在井下真实环境中采煤机的定位精度，在山东能源集团开展了井下采煤机机载融合定位试验。
3.1 地面采煤机融合定位试验
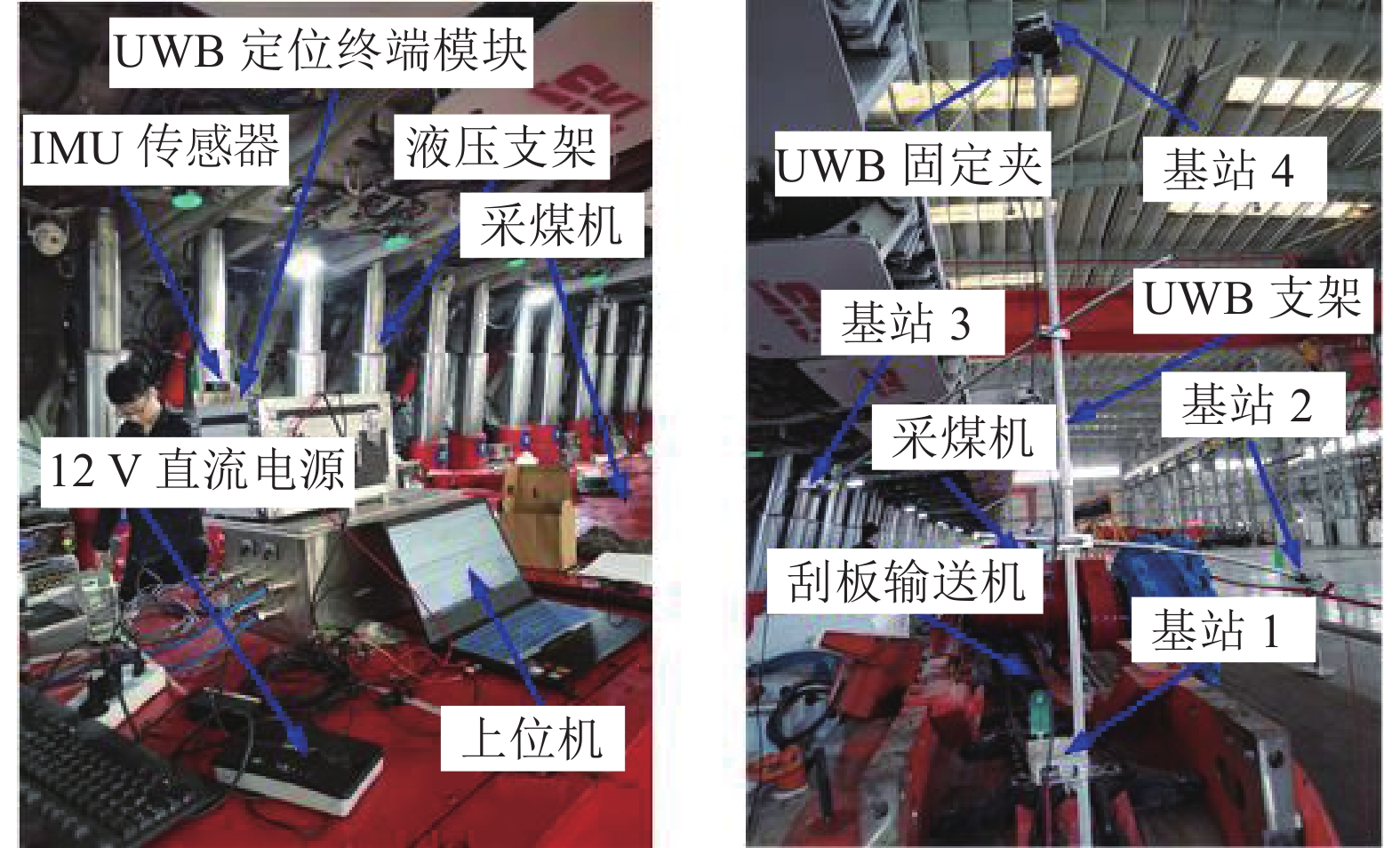
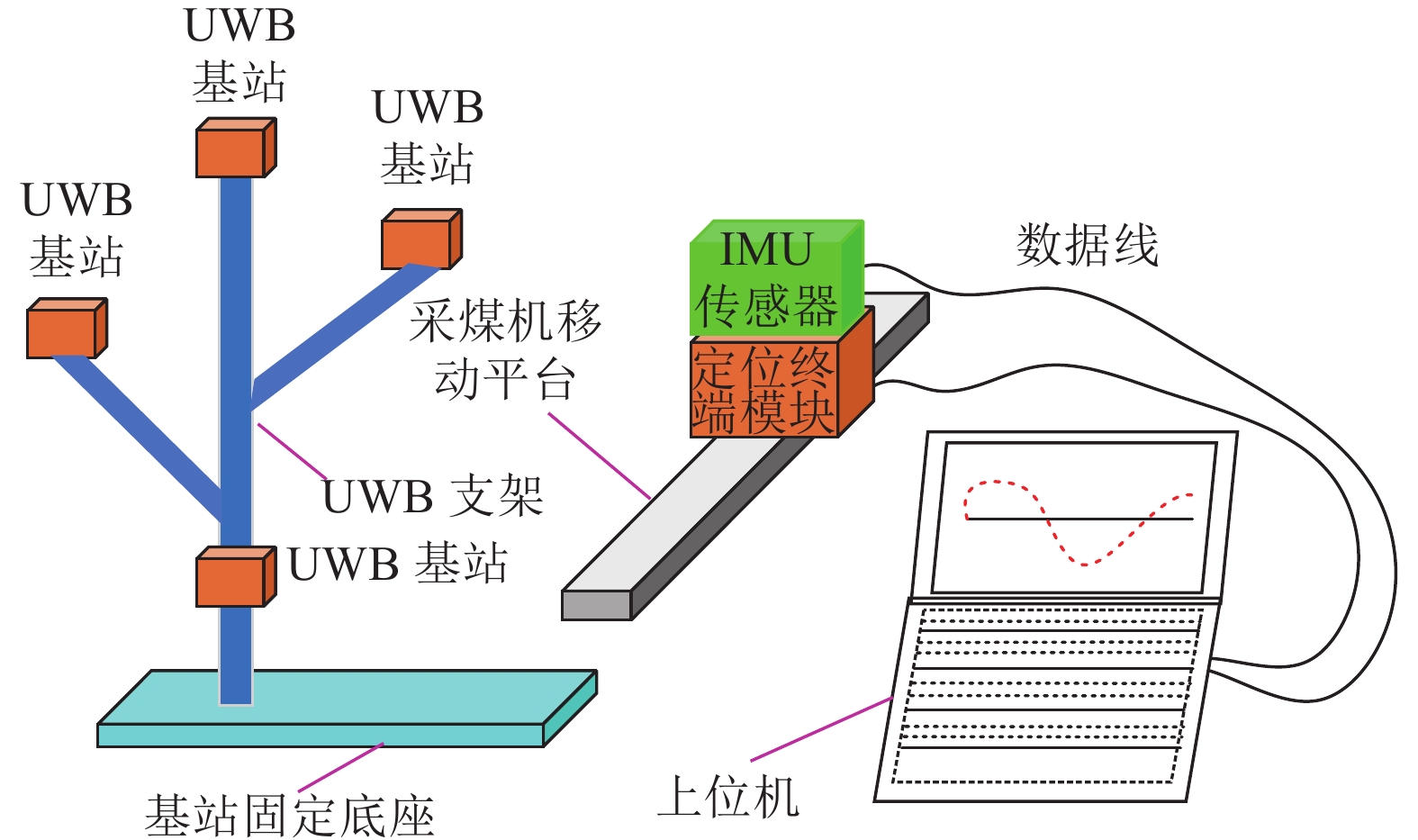
以太原重型机械集团有限公司的MG250/600-AWD智能型交流电牵引采煤机为试验载体，将定位终端和IMU固定在采煤机机身上的重心位置，而且IMU放置在定位终端的上方位置，4个UWB基站安装在自制支架上，调整4个基站的相对位置并用螺钉进行固定，4个UWB基站在水平面的投影呈V型，该布局方案有利于获得较高估计精度[28]，表1和表2给出IMU传感器和UWB模块的主要性能参数。定位终端和IMU传感器通过数据线与上位机连接，利用相应的软件分别对UWB系统和IMU系统的相关数据信息进行采集，设置IMU系统的采集频率为100 Hz, UWB系统的输出频率接近40 Hz，试验场地及试验布局情况如图2所示，图3给出了融合定位试验原理的示意图。在定位过程中，设置采煤机的运动速度为4 m/min，采煤机上的定位终端与4个UWB基站的信号传输通道均处于视距环境中。在采煤机的端头选择合适的位置建立坐标系，作为IMU系统和UWB系统的导航坐标系，利用卷尺和高精度莱卡激光测距仪测量标定4个基站在导航坐标系下的位置坐标，表3给出了地面采煤机机载定位时4个UWB基站的三维位置坐标。
表 1 IMU传感器的主要参数指标Table 1. Main parameters of IMU sensor部件 最大量程 最大输出频率/Hz 陀螺仪 ±2000(°)/s 200 加速度计 ±16 g 200 地磁计 800 mG 200 角度 ±180°/ ±90° 200 表 2 UWB模块的主要参数指标Table 2. Main parameters of UWB module功率/μW 电压/V 频率/GHz 中心频率/GHz 刷新率/Hz 50 5 3.1~ 4.8 4.3 125 ![]()
图 2 地面采煤机IMU/UWB融合定位试验场景Figure 2. Experimental scenario of IMU/UWB fusion positioning for the ground shearer表 3 4个UWB基站的位置坐标Table 3. Position coordinates of four UWB base stations基站编号 x/m y/m z/m 基站1 1.112 0.471 1.375 基站2 0.442 1.483 1.556 基站3 1.925 1.551 1.913 基站4 1.073 0.542 2.532 图4给出了IMU/UWB融合定位的定位轨迹。可以看到，IMU/UWB融合定位结果的轨迹比UWB单独求解的轨迹更靠近真实运动轨迹，主要是由于UWB的定位结果对IMU的漂移有一定的抑制作用，尤其是y轴和z轴方向的轨迹，表明融合定位方法的精度高于单纯UWB系统的定位精度。利用VB-UKF自适应算法分别对单纯UWB定位结果和IMU/UWB融合定位结果进行平滑处理，平滑后的定位轨迹比平滑前的轨迹更靠近实际轨迹，而且定位轨迹的波动程度明显减小，由于VB-UKF算法能自适应的估计时变的测量噪声，可以明显改善系统的估计精度，经过VB-UKF算法平滑修正后，定位精度进一步得到提升。相比于VB-UKF算法平滑纯UWB解算的定位轨迹，VB-UKF算法平滑融合定位结果的轨迹更逼近真实轨迹。
![]()
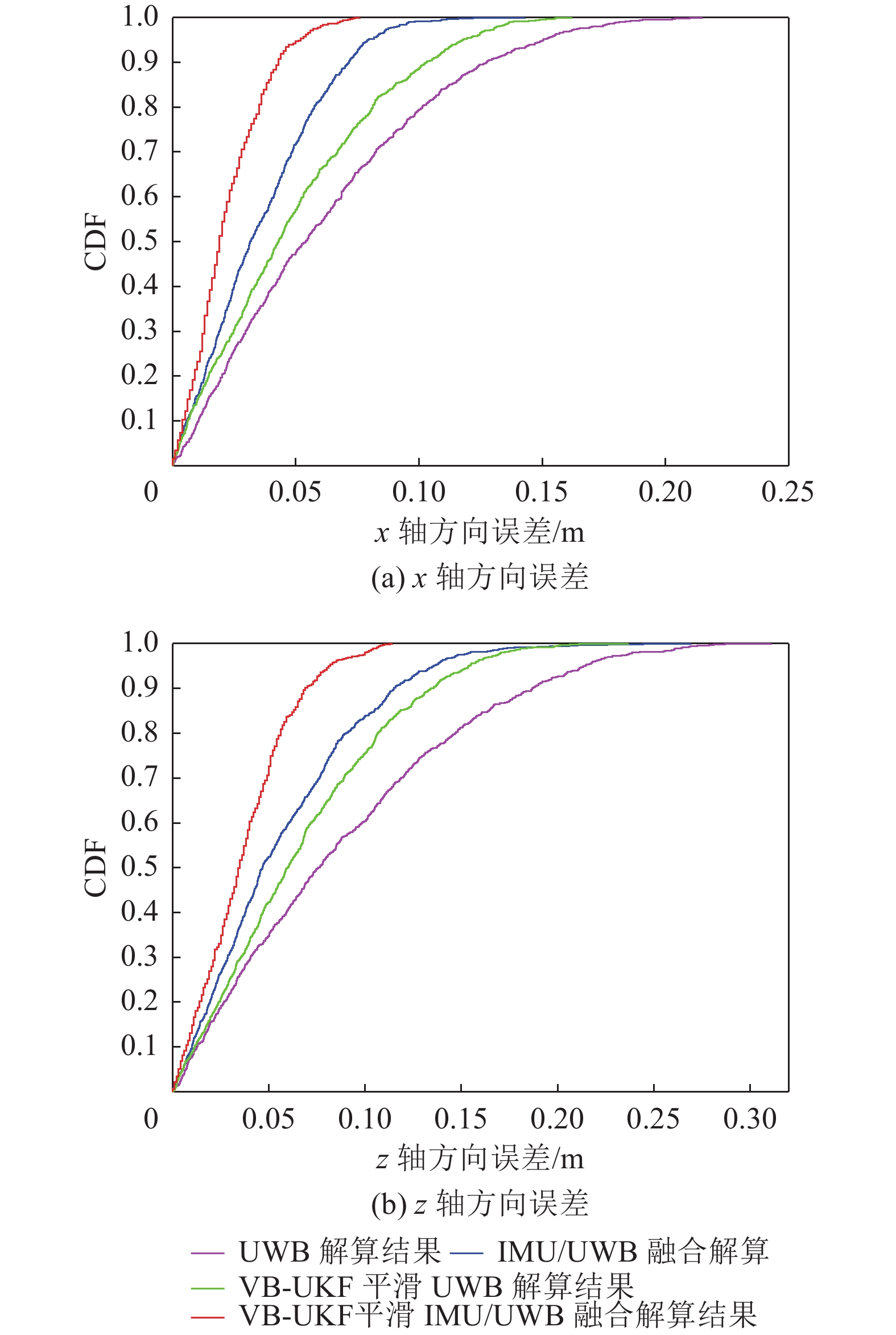
图 4 地面采煤机的IMU/UWB融合定位轨迹对比Figure 4. Comparison of the localization trajectory for IMU/UWB fusion of ground shearer machine-load experiment图5计算了x轴与z轴方向误差曲线，表4统计了x轴与z轴方向误差的均值和误差标准差，图6给出了x轴和z轴方向误差的CDF曲线。可以看出，IMU/UWB融合定位的x轴与z轴方向误差明显减小，融合定位方法的x轴和z轴方向的平均误差分别为0.037 m和0.057 m，相比UWB单独解算的结果，平均精度分别提高了40.3%和35.9%，说明融合定位方法能够提供更好的定位结果。融合定位的结果经过VB-UKF算法滤波平滑后，x轴和z轴误差波动程度有所减小，x轴和z轴方向的平均误差分别为0.022 m和0.041 m，较平滑前平均精度提升了40.5%和39%。当CDF达到90%时，经过平滑后融合定位方法的x轴和z轴方向的误差分别由0.072 m 和0.115 m减小为0.069 m 和0.043 m，表明VB-UKF算法对融合定位结果的修正作用明显。
![]()
图 5 地面采煤机试验的IMU/UWB融合定位结果的x轴和z轴方向误差曲线Figure 5. Localization error curves of x-axis and z-axis direction for results of IMU/UWB fusion positioning in ground shearer experiment表 4 地面采煤机定位的x轴和z轴方向定位误差统计Table 4. Localization error statistics on x- and z-axis direction for results of ground shearer positioning解算方法 误差/m 最大 平均 标准差 UWB单独解算 x: 0.215
z: 0.311x: 0.062
z: 0.089x: 0.045
z: 0.066VB-UKF平滑UWB结果 x: 0.162
z: 0.236x: 0.049
z: 0.067x: 0.036
z: 0.046IMU/UWB融合解算 x: 0.143
z: 0.269x: 0.036
z: 0.057x: 0.025
z: 0.041VB-UKF平滑IMU/UWB融合结果 x: 0.076
z: 0.114x: 0.022
z: 0.038x: 0.016
z: 0.024![]()
图 6 地面采煤机试验的IMU/UWB融合定位结果x轴和z轴方向定位误差的CDF曲线Figure 6. CDF curves of x-axis and z-axis directional localization error for results of IMU/UWB fusion positioning of ground shearer experiment3.2 井下采煤机融合定位试验
为探究IMU/UWB融合定位方法在井下现场环境中采煤机的定位精度，在山东省邹城市山东能源集团济三采煤工作面端头开展采煤机机载定位试验，将定位终端模块和IMU固定在采煤机的机身上，并且IMU放置在定位终端的正上方，采用强力双面胶和胶带将定位终端粘贴固定采煤机机身上，根据采煤工作面端头的实际环境，选择4个易于安装测量的位置，将UWB基站布局在采煤工作面端头的这4个位置，并用胶带黏胶固定，井下试验环境及4个基站的布局状况如图7所示，其定位原理如3所示。在井下采煤机机载定位过程中，定位终端与所有基站的信号传输通道内没有明显较大的障碍物遮挡，在井下采煤工作面巷道的端头处选择合适的位置作为导航坐标系的原点，并建立导航坐标系，利用高精度莱卡激光测距仪测量标定4个基站在导航坐标系下的位置坐标，表5给出了井下采煤机机载定位时4个UWB基站的三维位置坐标。
![]()
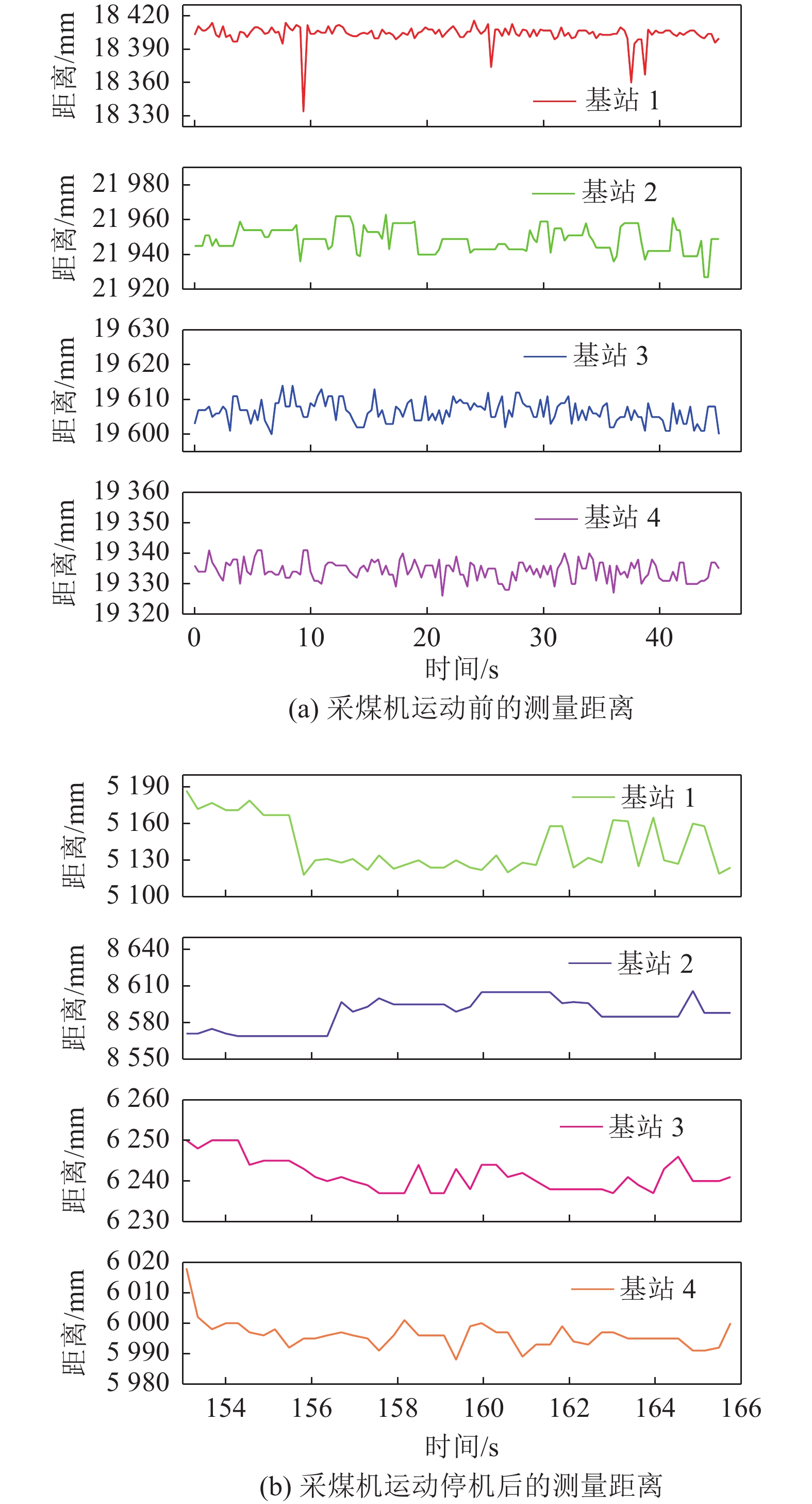
图 7 井下采煤机IMU/UWB 融合定位现场试验场景Figure 7. Field experimental scenario of IMU/UWB integrated positioning system of shearer in underground coal mine environment表 5 井下现场试验4个UWB基站的坐标Table 5. Position coordinates of four UWB base stations in the underground field experiment基站编号 x/m y/m z/m 1 1.251 3.352 −0.251 2 0 0 0 3 −0.110 2.375 0.311 4 −1.223 2.758 0.349 图8给出了采煤机运动前和停机后的没有异常值的测距变化情况，采煤机运动前45 s内(图8a)，UWB信号传输通道内没有任何障碍物，4个基站的测距波动幅值大约为2 cm，说明UWB P440在井下环境的测距相对稳定，周围环境对信号的传播影响较小；基站1的测距有突变点，主要是由于基站1放置在采煤工作面端头的金属体上，不可避免地受到端头金属体的反射引起多径效应。采煤机停机后的几秒内水雾和粉尘不会立刻消失，即采煤机处于静止状态时信号通道内存在水雾和粉尘，图8b为采煤机停机后153～166 s内的测距变化情况，可以看到，基站1和基站2的测距波动幅值大约为5 cm，基站3和基站4的测距波动范围大约为2 cm，随着时间的增加，粉尘和水雾逐渐减少，4个基站的测距逐渐趋于平稳状态，测距波动范围为2 cm，从测距的波动幅值来看，粉尘和水雾对UWB信号的影响相对较小，可能是由于采煤机停机后水雾和粉尘的浓度降低的原因。
![]()
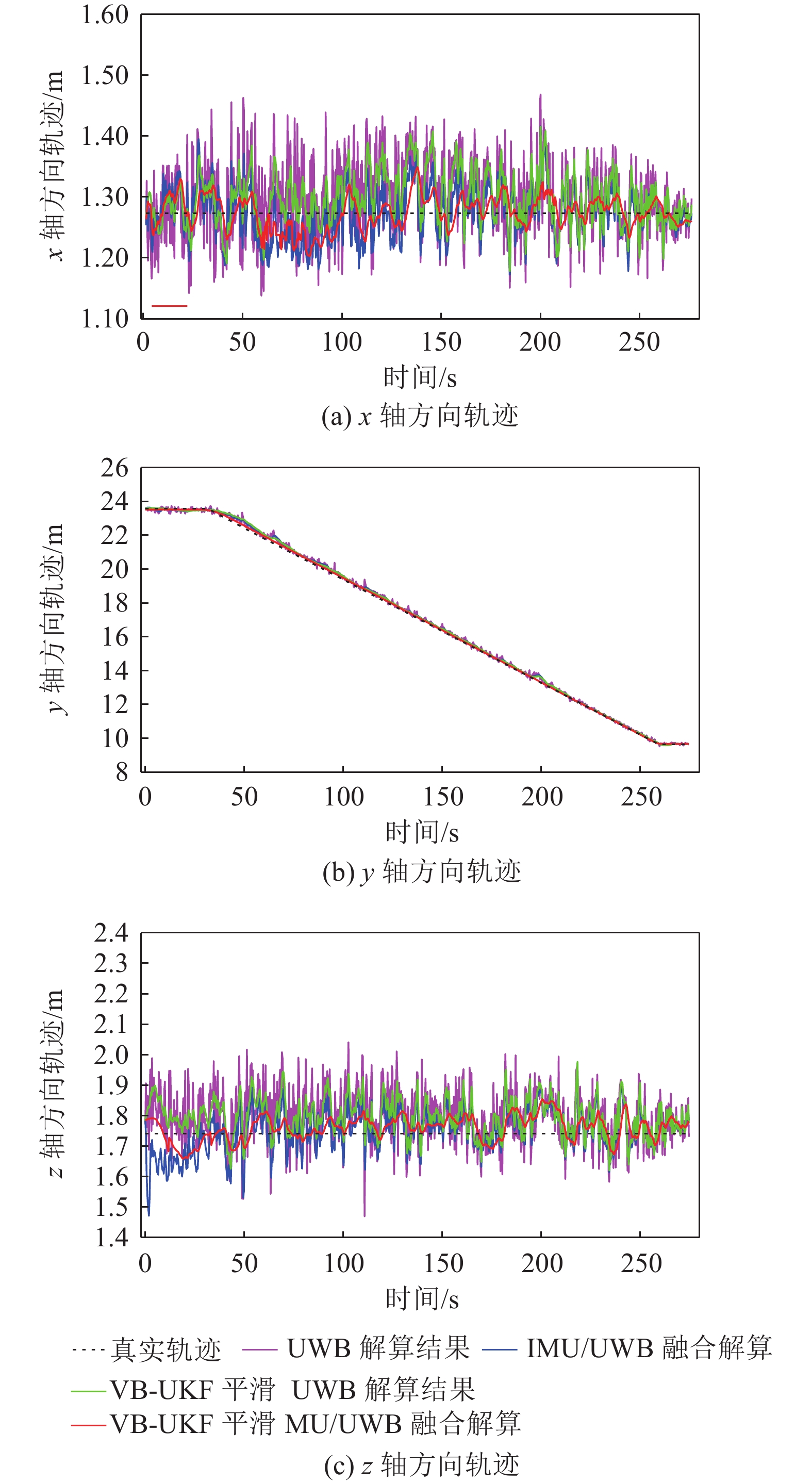
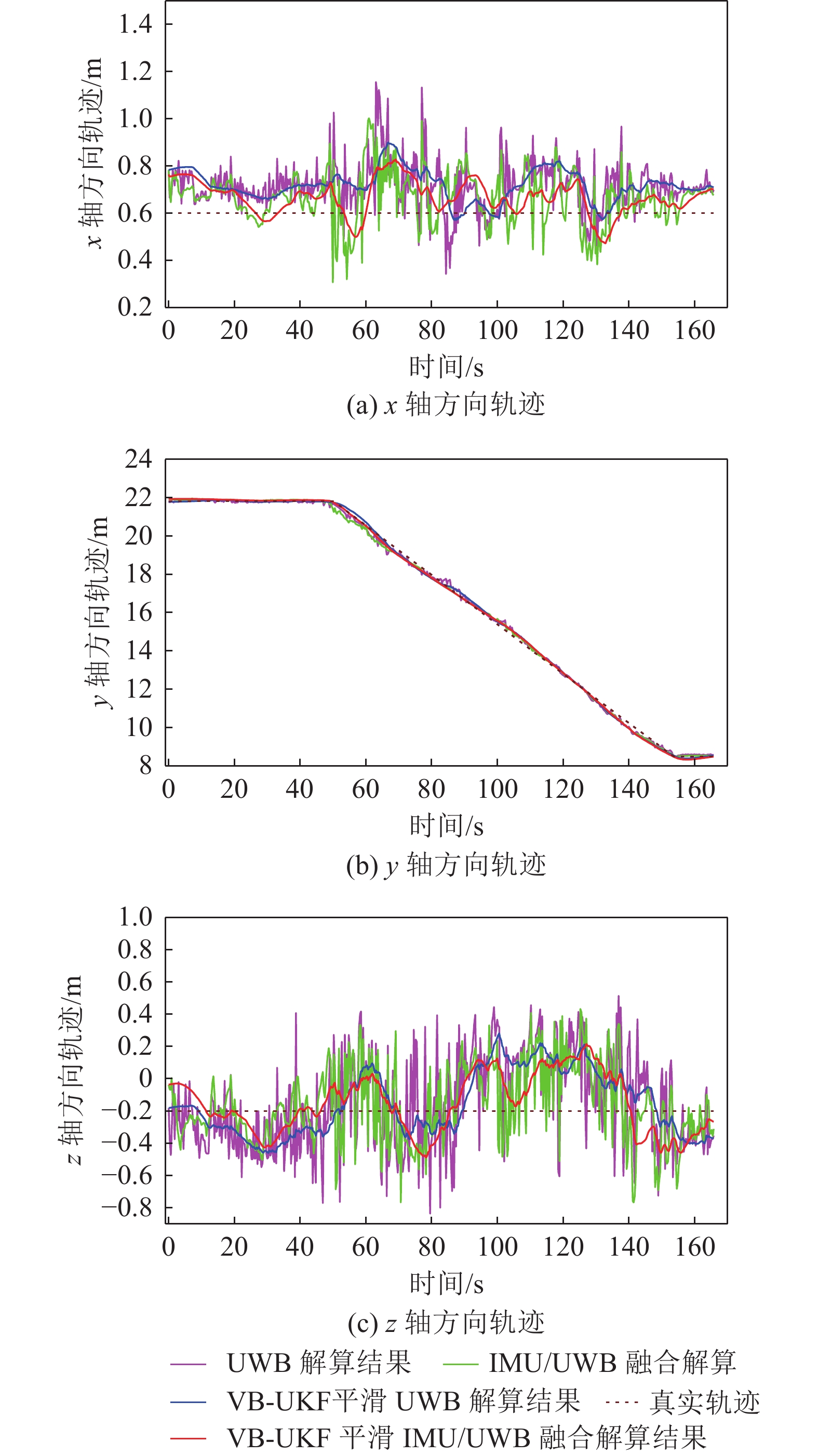
图 8 井下环境采煤机运动前和停机后4个基站测量距离Figure 8. Measurement distance of four base stations before the shearer movement and shutdown in the underground coal mine environment图9为井下采煤机机载试验时IMU/UWB融合定位方法的定位轨迹对比，结果显示，在采煤机处于静止状态时（图9的前45 s），纯UWB单独解算和IMU/UWB融合解算的定位轨迹波动较小，且靠近真实轨迹；采煤机截割煤层时（图9的前45~153 s），融合定位方法求解的轨迹比纯UWB解算的轨迹更接近真实轨迹，说明IMU/UWB融合定位方法能够很好的修正采煤机的位置偏差，提升了端头定位的精度；利用VB-UKF自适应算法平滑定位过程中动态变化的测量噪声，提升了定位轨迹的平滑性，使得融合定位方法的定位轨迹更进一步逼近真实轨迹[29]。
![]()
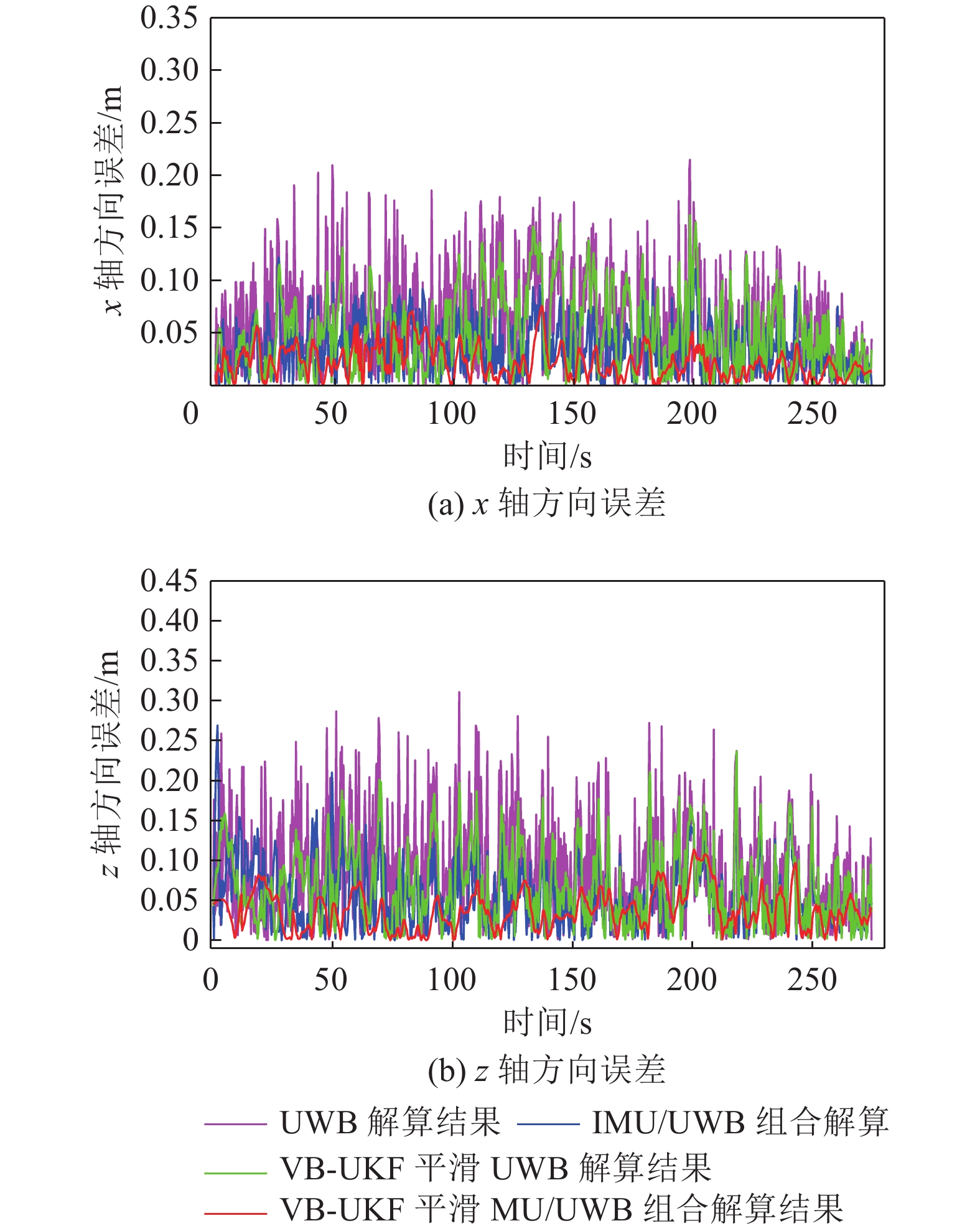
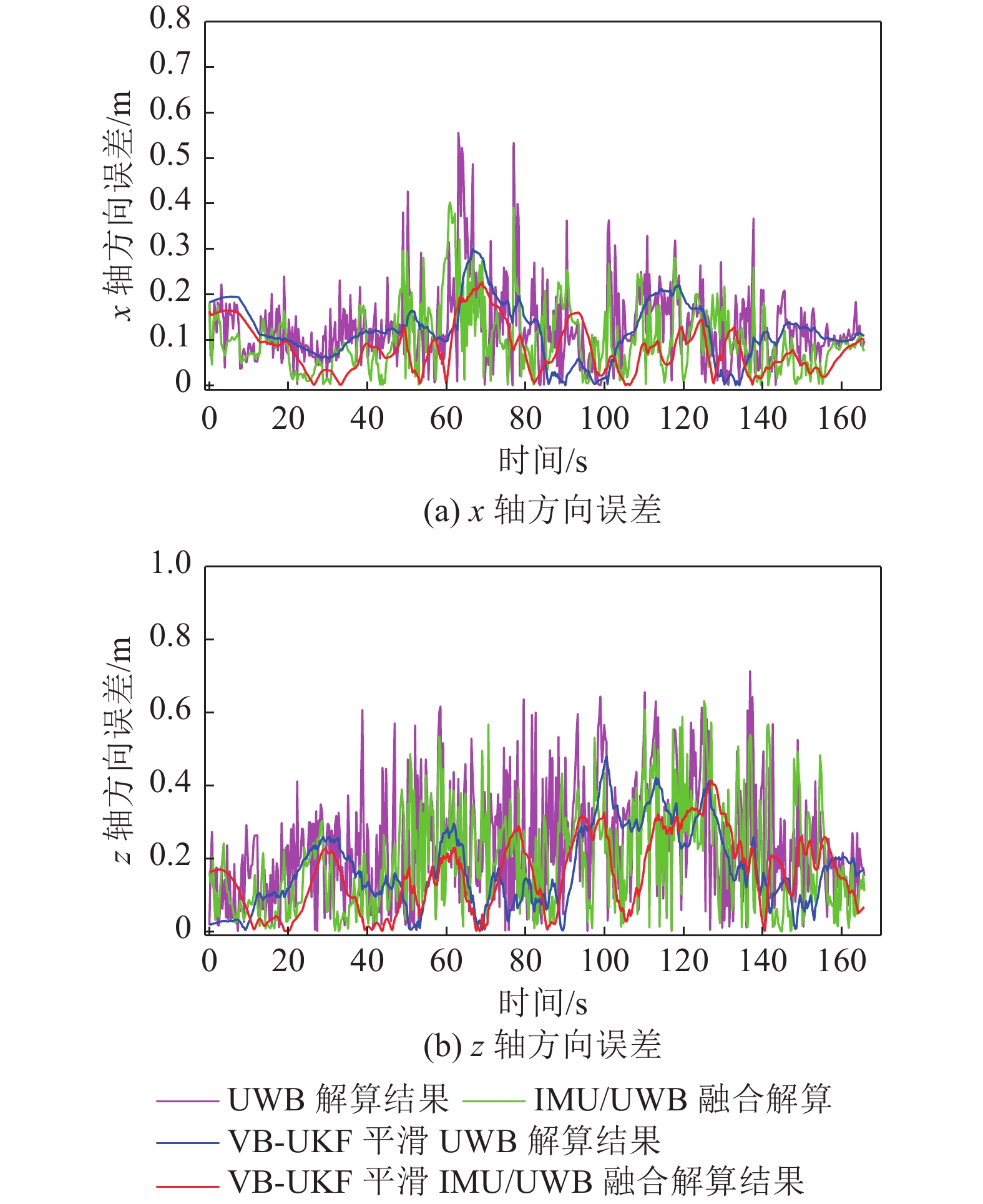
图 9 井下采煤机机载试验融合方法的定位轨迹Figure 9. Localization trajectory of fusion method in underground coalmine shearer machine-load experiment基于图9井下采煤机机载试验定位轨迹计算x轴与z轴方向误差，如图10所示。可以看到，UWB单独解算时x轴和z轴方向误差大于融合定位方法的误差，z轴方向的误差大于x轴方向的误差且波动明显，这是由于受到山东能源集团济三工作面端头空间环境的限制，布局UWB基站时基站之间的高度差（z轴方向坐标）较小，即UWB基站在z轴方向的分散性差，从而导致z轴方向的误差较大。利用VB-UKF算法平滑定位结果后，纯UWB单独定位的误差和融合定位的误差都进一步减小，由于VB-UKF算法能够自适应的调整测量噪声，提高系统的估计精度；相比纯UWB单独解算经过平滑后的结果，融合定位的结果经过VB-UKF自适应算法平滑后位置偏差得到了较明显的修正，使得误差进一步减小且误差波动范围更小，具有更高的定位精度。
![]()
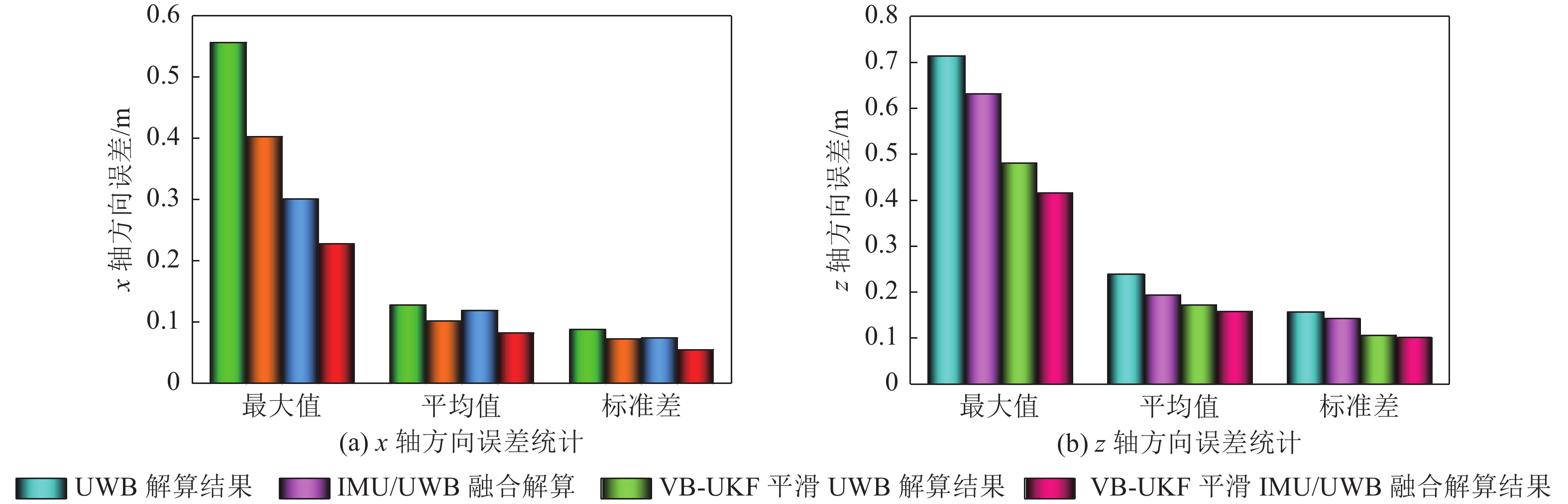
图 10 井下采煤机机载试验融合定位结果的x轴和z轴方向定位误差曲线Figure 10. Localization error curves of x-axis and z-axis direction for results of fusion positioning in underground coalmine shearer machine-load experiment图11给出了x轴和z轴方向误差的最大值、均值及标准差，可以看到，融合定位方法的x轴与z轴方向的最大误差、平均误差和误差标准差比纯UWB单独解算的都小，UWB单独解算的x轴和z轴平均误差分别为0.128 m和0.239 m，融合定位方法的平均误差分别为0.102 m和0.194 m，平均精度对应的提升了20.3%和18.8%；经过VB-UKF算法平滑处理后，融合定位方法的x轴与z轴方向的平均误差进一步减小为0.082 m和0.158 m，相较于平滑前的融合定位，平均精度分别提升了19.6%和18.6%。
![]()
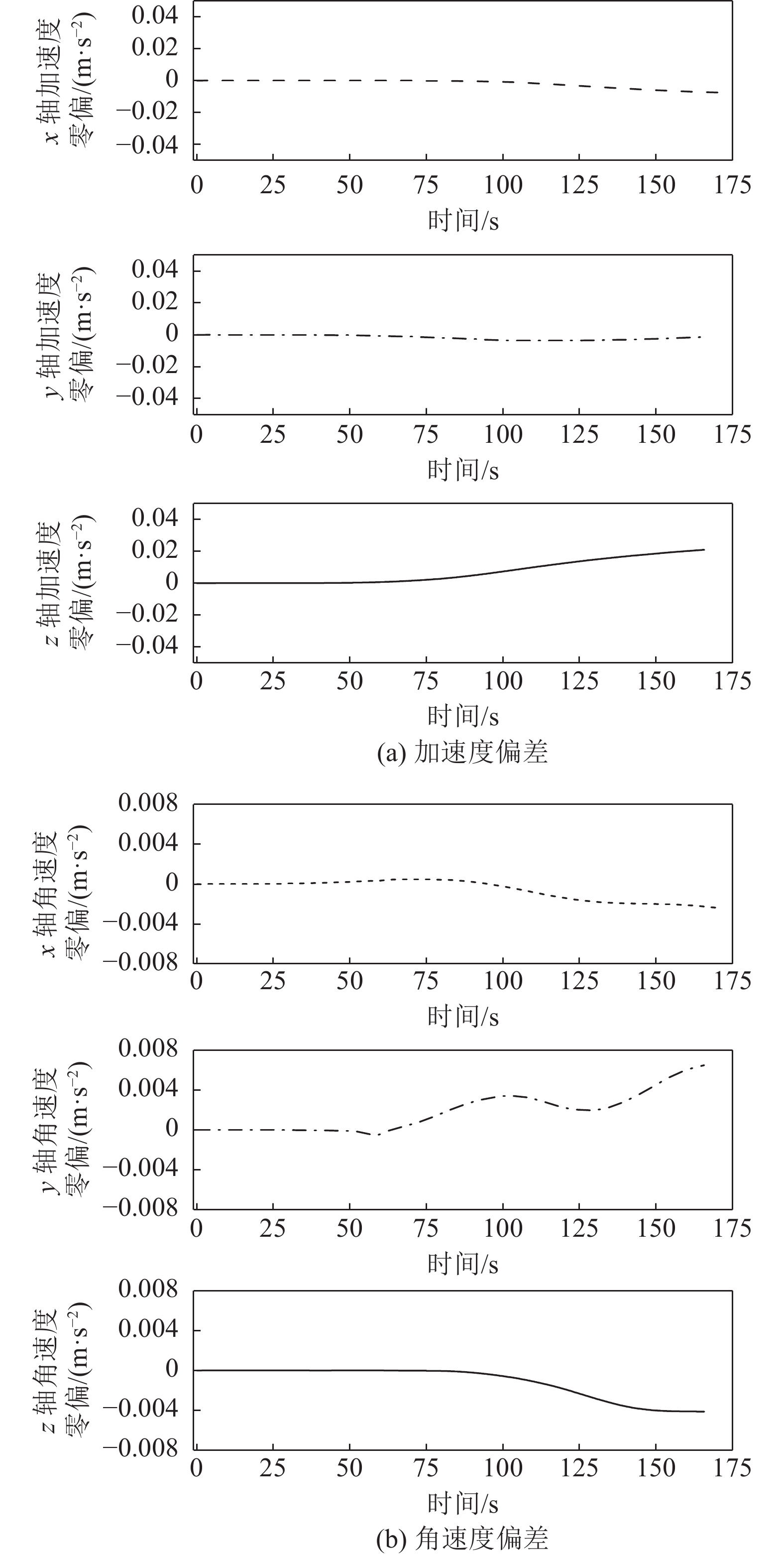
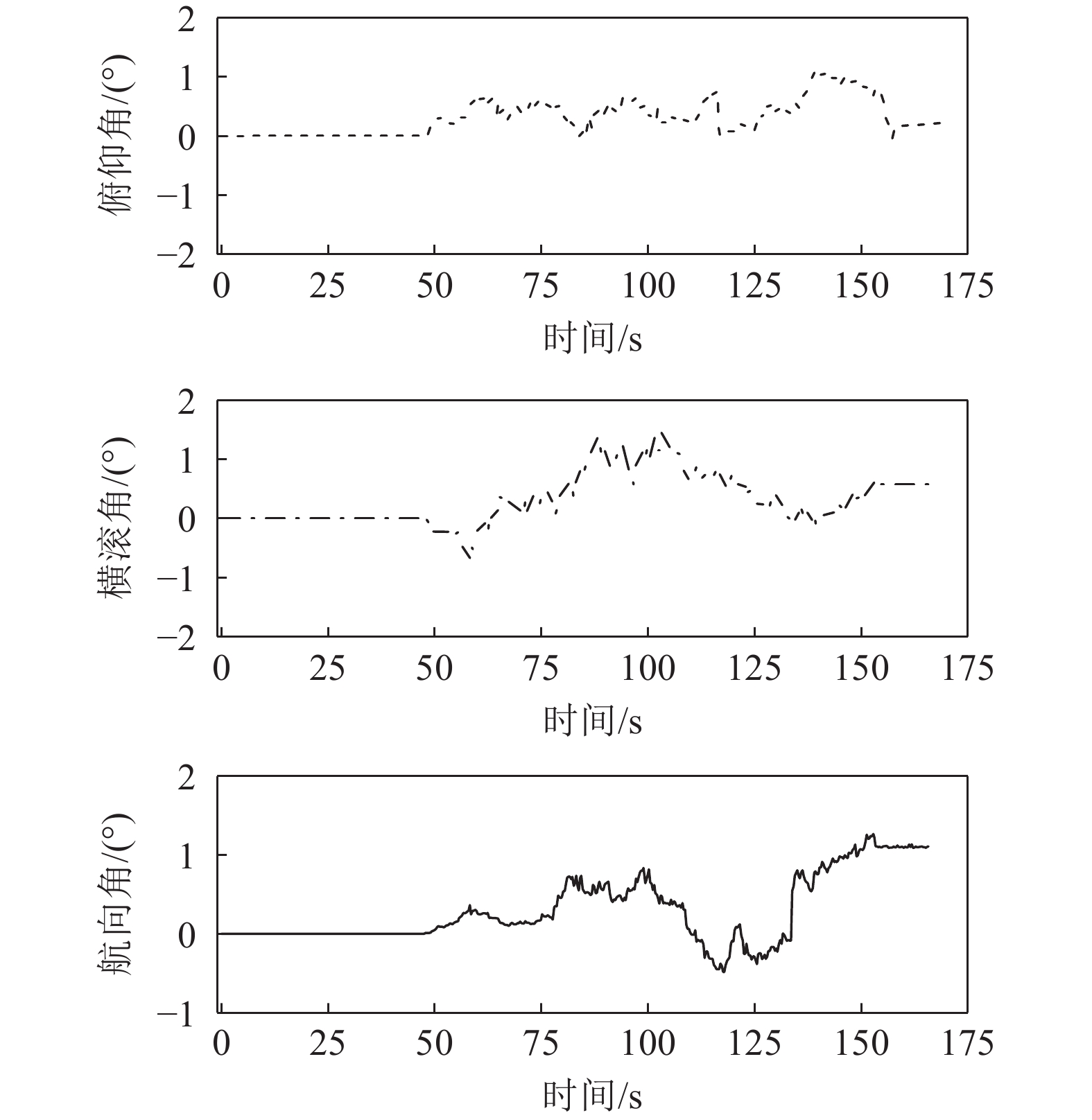
图 11 井下采煤机机载试验融合定位结果的误差统计Figure 11. Localization error statistics for results of tight fusion in underground coalmine shearer machine-load experiment图12给出了融合定位过程中IMU的加速度偏差和角速度偏差的变化曲线，图13为融合定位时姿态角的变化曲线。可以看出，加速度偏差和角速度偏差相对较小，主要是由于端头定位时采煤机的行走距离较短（10 m左右），IMU系统中的惯性原件漂移相对较弱，同时在融合系统中利用误差EKF算法实时补偿IMU的偏差，从而对IMU的偏差得到了有效的补偿修正。在试验开始前，调整刮板输送机的位置使其处于直线状态（图7），在试验过程中采煤机的摇臂始终处于水平状态，定位终端模块放置在机身的水平面上，俯仰角和横滚角近似为0，图13结果显示3个姿态角的误差小于2°，表明融合系统能够有效的约束IMU姿态角的漂移。
![]()
图 12 采煤机定位过程中IMU的加速度偏差和角速度偏差变化曲线Figure 12. Variation curve of acceleration and angular velocity bias for IMU during the shearer positioning![]()
图 13 采煤机定位过程中融合定位的姿态角变化曲线Figure 13. Variation curve of attitude for fusion positioning during the shearer positioning对比2个试验结果，地面采煤机定位精度高于井下采煤机定位精度，由于地面采煤机端头定位时基站按照V型布局方式布设基站，采煤机运动过程没有截割煤层，运动平稳振动较小；在井下环境定位时，受到济三薄煤层工作面端头有限空间的限制，使得基站在高度方向分散性差，采煤机运动时连续的截割煤层产生相对较大的振动，而且在信号传输通道存在大量的粉尘和水雾，从而导致了井下采煤机定位效果相对较差。但是可以肯定的是UWB定位系统在井下具有较好的应有前景，所提IMU/UWB融合定位方法的结果经过VB-UKF算法平滑处理后能获得较好的定位精度。
4. 结 论
1）为保证采煤机长期自动开采的定位精度，构建了基于IMU/UWB融合定位模型，提出了采煤工作面端头自主修正补偿惯性导航定位装置的漂移误差，利用IMU/UWB的融合结果对惯性导航定位装置的位置和姿态进行自动纠偏，从而实现采煤机长期自主循环截割；为了减小不确定测量噪声对定位结果的影响，提出了利用VB-UKF算法对定位结果进行平滑处理。
2）井下采煤机机载试验结果表明，IMU/UWB融合定位精度高于UWB系统单独解算的精度；经过VB-UKF算法平滑处理后，定位精度进一步得到提升，x轴和z轴方向的平均精度分别提升了19.6%和18.6%；3个姿态角的误差小于2°，利用误差扩展卡尔曼滤波实时补偿修正IMU的偏差，有效地抑制IMU姿态角的漂移。
3）利用IMU/UWB融合定位模型获得了采煤工作面端头区域采煤机的准确位置，为采煤机惯性导航定位装置提供动态自主校准的基准。井下现场定位试验证明了采煤工作面端头定位方法的有效性，为井下IMU/UWB融合定位方法的应用提供较好的参考和经验。
-
![]()
图 1 采煤工作面端头采煤机自主定位系统结构
Figure 1. Structure of the shearer autonomous positioning system of the coal mining face end
![]()
图 2 地面采煤机IMU/UWB融合定位试验场景
Figure 2. Experimental scenario of IMU/UWB fusion positioning for the ground shearer
![]()
图 4 地面采煤机的IMU/UWB融合定位轨迹对比
Figure 4. Comparison of the localization trajectory for IMU/UWB fusion of ground shearer machine-load experiment
![]()
图 5 地面采煤机试验的IMU/UWB融合定位结果的x轴和z轴方向误差曲线
Figure 5. Localization error curves of x-axis and z-axis direction for results of IMU/UWB fusion positioning in ground shearer experiment
![]()
图 6 地面采煤机试验的IMU/UWB融合定位结果x轴和z轴方向定位误差的CDF曲线
Figure 6. CDF curves of x-axis and z-axis directional localization error for results of IMU/UWB fusion positioning of ground shearer experiment
![]()
图 7 井下采煤机IMU/UWB 融合定位现场试验场景
Figure 7. Field experimental scenario of IMU/UWB integrated positioning system of shearer in underground coal mine environment
![]()
图 8 井下环境采煤机运动前和停机后4个基站测量距离
Figure 8. Measurement distance of four base stations before the shearer movement and shutdown in the underground coal mine environment
![]()
图 9 井下采煤机机载试验融合方法的定位轨迹
Figure 9. Localization trajectory of fusion method in underground coalmine shearer machine-load experiment
![]()
图 10 井下采煤机机载试验融合定位结果的x轴和z轴方向定位误差曲线
Figure 10. Localization error curves of x-axis and z-axis direction for results of fusion positioning in underground coalmine shearer machine-load experiment
![]()
图 11 井下采煤机机载试验融合定位结果的误差统计
Figure 11. Localization error statistics for results of tight fusion in underground coalmine shearer machine-load experiment
![]()
图 12 采煤机定位过程中IMU的加速度偏差和角速度偏差变化曲线
Figure 12. Variation curve of acceleration and angular velocity bias for IMU during the shearer positioning
![]()
图 13 采煤机定位过程中融合定位的姿态角变化曲线
Figure 13. Variation curve of attitude for fusion positioning during the shearer positioning
表 1 IMU传感器的主要参数指标
Table 1 Main parameters of IMU sensor
部件 最大量程 最大输出频率/Hz 陀螺仪 ±2000(°)/s 200 加速度计 ±16 g 200 地磁计 800 mG 200 角度 ±180°/ ±90° 200 
下载: 导出CSV
表 2 UWB模块的主要参数指标
Table 2 Main parameters of UWB module
功率/μW 电压/V 频率/GHz 中心频率/GHz 刷新率/Hz 50 5 3.1~ 4.8 4.3 125
下载: 导出CSV
表 3 4个UWB基站的位置坐标
Table 3 Position coordinates of four UWB base stations
基站编号 x/m y/m z/m 基站1 1.112 0.471 1.375 基站2 0.442 1.483 1.556 基站3 1.925 1.551 1.913 基站4 1.073 0.542 2.532
下载: 导出CSV
表 4 地面采煤机定位的x轴和z轴方向定位误差统计
Table 4 Localization error statistics on x- and z-axis direction for results of ground shearer positioning
解算方法 误差/m 最大 平均 标准差 UWB单独解算 x: 0.215
z: 0.311x: 0.062
z: 0.089x: 0.045
z: 0.066VB-UKF平滑UWB结果 x: 0.162
z: 0.236x: 0.049
z: 0.067x: 0.036
z: 0.046IMU/UWB融合解算 x: 0.143
z: 0.269x: 0.036
z: 0.057x: 0.025
z: 0.041VB-UKF平滑IMU/UWB融合结果 x: 0.076
z: 0.114x: 0.022
z: 0.038x: 0.016
z: 0.024
下载: 导出CSV
表 5 井下现场试验4个UWB基站的坐标
Table 5 Position coordinates of four UWB base stations in the underground field experiment
基站编号 x/m y/m z/m 1 1.251 3.352 −0.251 2 0 0 0 3 −0.110 2.375 0.311 4 −1.223 2.758 0.349
下载: 导出CSV
-
[1] 葛世荣,郝雪弟,田 凯,等. 采煤机自主导航截割原理及关键技术[J]. 煤炭学报,2021,46(3):774−788. doi: 10.13225/j.cnki.jccs.yt21.0114 GE Shirong,HAO Xuedi,TIAN Kai,et al. Principle and key technology of autonomous navigation cutting for deep coal seam[J]. Journal of China Coal Society,2021,46(3):774−788. doi: 10.13225/j.cnki.jccs.yt21.0114
[2] 王世博,葛世荣,王世佳,等. 长壁综采工作面无人自主开采发展路径与挑战[J]. 煤炭科学技术,2022,50(2):231−243. doi: 10.13199/j.cnki.cst.2020-1150 WANG Shibo,GE Shirong,WANG Shijia,et al. Development and challenge of unmanned autonomous longwall fully-mechanized coal mining face[J]. Coal Science and Technology,2022,50(2):231−243. doi: 10.13199/j.cnki.cst.2020-1150
[3] 鲁 程,王世博,葛世荣,等. 多惯导冗余的采煤机定位原理及其合理性分析[J]. 煤炭学报,2019,44(S2):746−753. doi: 10.13225/j.cnki.jccs.2019.0491 LU Cheng,WANG Shibo,GE Shirong,et al. Redundant multi-INS positioning algorithm of shearer and analysis of its rationality[J]. Journal of China Coal Society,2019,44(S2):746−753. doi: 10.13225/j.cnki.jccs.2019.0491
[4] SCHIFFBAUERW H. Navigation and control of continuous mining systems for coal mining[C]. IEEE Industry Applications Conference Thirty-First IAS Annual Meeting. 1996, 4: 2473-2479.
[5] SCHIFFBAUER W H. Accurate navigation and control of continuous mining machines for coal mining [J]. U. S. Dept of health and human services, 1997.
[6] REID P B, DUNN M T, REID D C, et al. Real-world automation: New capabilities for underground longwall mining[A]. Proceedings of the 2010 Australasian Conference on Robotics and Automation 2010 [C]. Brisbane: Queensland University Fechnology, 2010.
[7] RALSTON J C,REID D C,DUNN M T,et al. Longwall automation: Delivering enabling technology to achieve safer and more productive underground mining[J]. International Journal of Mining Science and Technology,2015,25(6):865−876. doi: 10.1016/j.ijmst.2015.09.001
[8] 方新秋,何 杰,张 斌,等. 无人工作面采煤机自主定位系统[J]. 西安科技大学学报,2008,28(2):349−353. doi: 10.3969/j.issn.1672-9315.2008.02.033 FANG Xinqiu,HE Jie,ZHANG Bin,et al. Self-positioning system of the shearer in unmanned workface[J]. Journal of Xi’an University of Science and Technology,2008,28(2):349−353. doi: 10.3969/j.issn.1672-9315.2008.02.033
[9] FAN Qigao,LI Wei,LUO Chengming. Error analysis and reduction for shearer positioning using the strapdown inertial navigation system[J]. International Journal of Computer Science Issues,2012,9(1):49−54.
[10] 张博渊,王世博,葛世荣. 惯性导航初始对准偏差与安装偏差对采煤机定位精度影响及其校准方法[J]. 煤炭学报,2017,42(3):789−795. ZHANG Boyuan,WANG Shibo,GE Shirong. Effects of initial alignment error and installation noncoincidence on the shearer positioning accuracy and calibration method[J]. Journal of China Coal Society,2017,42(3):789−795.
[11] 郝尚清,李 昂,王世博,等. 采煤机惯性导航安装偏差对定位误差的影响[J]. 煤炭学报,2015,40(8):1963−1968. doi: 10.13225/j.cnki.jccs.2014.1561 HAO Shangqing,LI Ang,WANG Shibo,et al. Effects of shearer inertial navigation installation noncoincidence on shearer positioning error[J]. Journal of China Coal Society,2015,40(8):1963−1968. doi: 10.13225/j.cnki.jccs.2014.1561
[12] HOL J D, DIJKSTRA F, LUINGE H, et al. Tightly coupled UWB/IMU pose estimation[C]. IEEE International Conference on Ultra-wideband, 2009: 688−692.
[13] WEN Kai,YU Kegen,LI Yingbing,et al. A new quaternion Kalman filter based foot-mounted IMU and UWB tightly-coupled method for indoor pedestrian navigation[J]. IEEE Transactions on Vehicular Technology,2020,69(4):4340−4352. doi: 10.1109/TVT.2020.2974667
[14] MIRAGLIA G, MALEKI K N, HOOK L R. Comparison of two sensor data fusion methods in a tightly coupled UWB/IMU 3-D localization system[C]//International Conference on Engineering, Technology and Innovation, 2017: 611-618.
[15] WANG Yan,LI Xin. An improved robust EKF algorithm based on sigma points for UWB and foot-mounted IMU fusion positioning[J]. Journal of Spatial Science,2021,66(2):329−350. doi: 10.1080/14498596.2019.1632754
[16] 张斌飞,靳伍银. 基于UWB和IMU紧组合的室内定位导航算法[J]. 电子测量技术,2022,45(10):67−73. ZHANG Bingfei,JIN Wuyin. Indoor positioning and navigation algorithm based on UWB and IMU tightly coupled[J]. Electronic measurement technology,2022,45(10):67−73.
[17] 朱建斌,赵健康,崔 超,等. 基于EKF的UWB/IMU组合导航系统鲁棒性设计[J]. 计算机仿真,2020,37(12):47−52. doi: 10.3969/j.issn.1006-9348.2020.12.011 ZHU Jianbing,ZHAO Jiankang,CUI Chao,et al. Robustness Design of UWB/IMU Tightly Integrated Navigation and Positioning System Based on EKF[J]. Computer simulation,2020,37(12):47−52. doi: 10.3969/j.issn.1006-9348.2020.12.011
[18] 匡 兵,陈凤冉,田春月,等. 基于改进粒子滤波的超宽带与惯性测量单元融合定位算法[J]. 科学技术与工程,2020,20(30):12460−12466. doi: 10.3969/j.issn.1671-1815.2020.30.029 KUANG Bing,CHEN Fengran,TIAN Chunyue,et al. Unit fusion positioning algorithm of ultra-wideband and inertial measurement based on improved particle filtering[J]. Science Technology and Engineering,2020,20(30):12460−12466. doi: 10.3969/j.issn.1671-1815.2020.30.029
[19] 王春琦,孔祥琦,丁晓欢,等. 基于无迹卡尔曼滤波的IMU和UWB融合定位算法研究[J]. 南昌航空大学学报,2020,34(3):8−17. WANG Chunqi,KONG Xiangqi,DING Xiaohuan,et al. Unscented kalman filter based IMU and UWB fusion position algorithm[J]. Journal of Nanchang Hang Kong University,2020,34(3):8−17.
[20] YANG Hai, LUO Tao, LI Wei, et al. A stable SINS/UWB integrated positioning method of shearer based on the multimodel intelligent switching algorithm [J]. IEEE Access, 2019, 7: 2912829138.
[21] CUI Yuming,LIU Songyong,YAO Jian,et al. Integrated positioning system of unmanned automatic vehicle in coal mines[J]. IEEE Transactions on Instrumentation and Measurement,2021,70:1−13.
[22] LI Menggang,ZHU Hua,YOU Shaoze,et al. UWB-based localization system aided with inertial sensor for underground coal mine applications[J]. IEEE Sensors Journal,2020,20(12):6652−6669. doi: 10.1109/JSEN.2020.2976097
[23] FAN Qigao,LI Wei,JING Hui,et al. Integrated positioning for coal mining machinery in enclosed underground mine based on SINS/WSN[J]. The Scientific World Journal,2014(1):460415.
[24] SONG Yang,HSU Lita. Tightly coupled integrated navigation system via factor graph for UAV indoor localization[J]. Aerospace Science and Technology,2021,108:106370. doi: 10.1016/j.ast.2020.106370
[25] 许晓伟,赖际舟,吕 品,等. 基于采煤机工作面端头量测的改进因子图高精度自主定位方法研究[J]. 控制与决策,2022,37(8):2170−2176. XU Xiaowei,LAI Jizhou,LYU Pin,et al. Research on the highprecision autonomous positioning method based on the improved factor graph of the measurements at both ends of shearer working face[J]. Control and Decision,2022,37(8):2170−2176.
[26] LIU Fei,LI Xin,WANG Jian,et al. An adaptive UWB/MEMS-IMU complementary kalman filter for indoor location in NLOS environment[J]. Remote Sensing,2019,11(22):2628. doi: 10.3390/rs11222628
[27] SHI Qin,ZHAO Sihao,CUI Xiaowei,et al. Anchor self-localization algorithm based on UWB ranging and inertial measurements[J]. Tsinghua Science and Technology,2019,24(6):728−737. doi: 10.26599/TST.2018.9010102
[28] 曹 波,王世博,葛世荣,等. 基于校准补偿和VBUKF平滑的超宽带采煤机定位技术[J]. 煤炭科学技术,2022,50(8):210−219. CAO Bo,WANG Shibo,GE Shirong,et al. Localization technology of ultra-wideband for shearer based on calibration compensation and VBUKF smoothing[J]. Coal Science and Technology,2022,50(8):210−219.
[29] 葛世荣, 王世佳, 曹 波, 等. 智能采运机组自主定位原理与技术[J]. 煤炭学报, 2022, 47(1): 75-86. GE Shirong, WANG Shijia, CAO Bo, et al. Autonomous positioning principle and technology of intelligent shearer and conveyor [J], Journal of China Coal Society, 2022, 47(1): 75-86.
-
期刊类型引用(8)
1. 闫明，付翔，王然风，杨欣雨，刘彬. 基于鲁棒闭合路径校准的采煤机SINS/OD组合导航系统. 工矿自动化. 2025(05): 41-48 . 
百度学术
2. 杨艺，孙英杰，常亚军，刘斌斌，王科平. 基于链式基站坐标融合的采煤机定位方法. 工矿自动化. 2025(05): 49-56 . 百度学术
3. 陈伟崇，赵海伟，郭文孝. 基于UWB的煤矿井下设备自动控制方法. 矿山机械. 2024(01): 65-69 . 百度学术
4. 肖明国，张彪，康玉国，丁文，黄渊，郑学召. 面向钻孔救援的UWB雷达探测技术研究进展. 煤炭技术. 2024(06): 174-177 . 百度学术
5. 蔡建建，张卫辉，杨强. 基于机器视觉的井下连续采煤机定位方法分析. 中国机械. 2024(14): 72-76 . 百度学术
6. 朱飞洋，余科根，林贻若，张继悦. 顾及运动约束的自适应UWB/IMU组合定位方法. 测绘科学. 2024(04): 23-33 . 百度学术
7. 杨秀建，敖鹏，沈世全，杨义兴，皇甫尚昆. 面向复杂环境的UWB/LiDAR/IMU组合定位方法. 中国惯性技术学报. 2024(07): 654-662 . 百度学术
8. 韩梦辉，曹波，王世博，张华，朱万洁. 矩形矿井巷道内UWB路径损耗研究. 煤炭技术. 2024(10): 218-222 . 百度学术
其他类型引用(2)
计量
- 文章访问数: 147
- HTML全文浏览量: 33
- PDF下载量: 52
- 被引次数: 10
