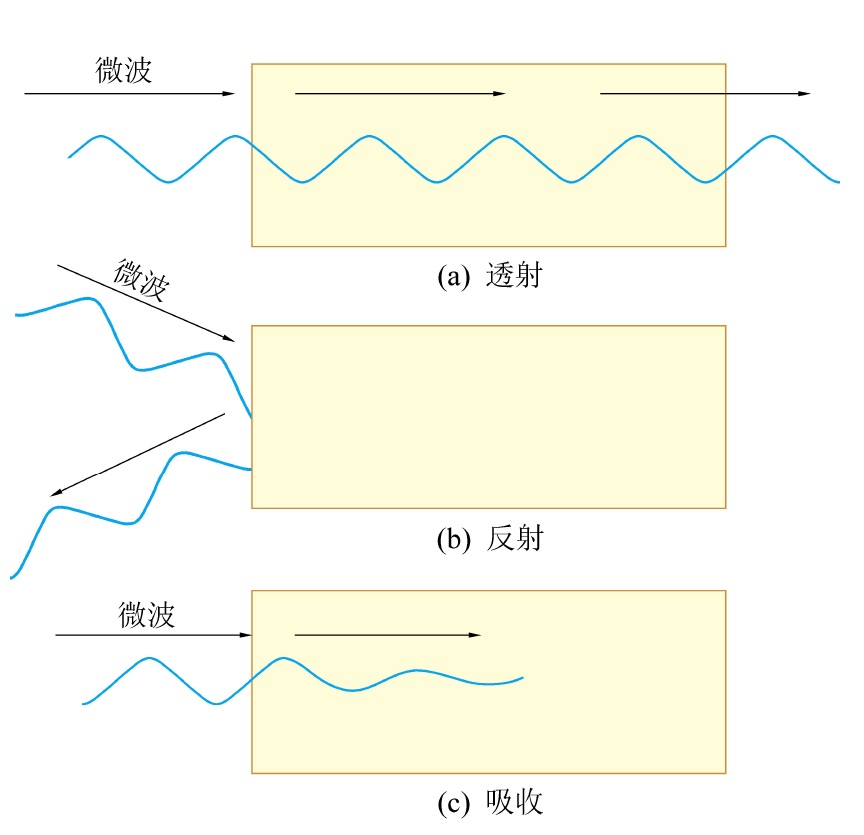
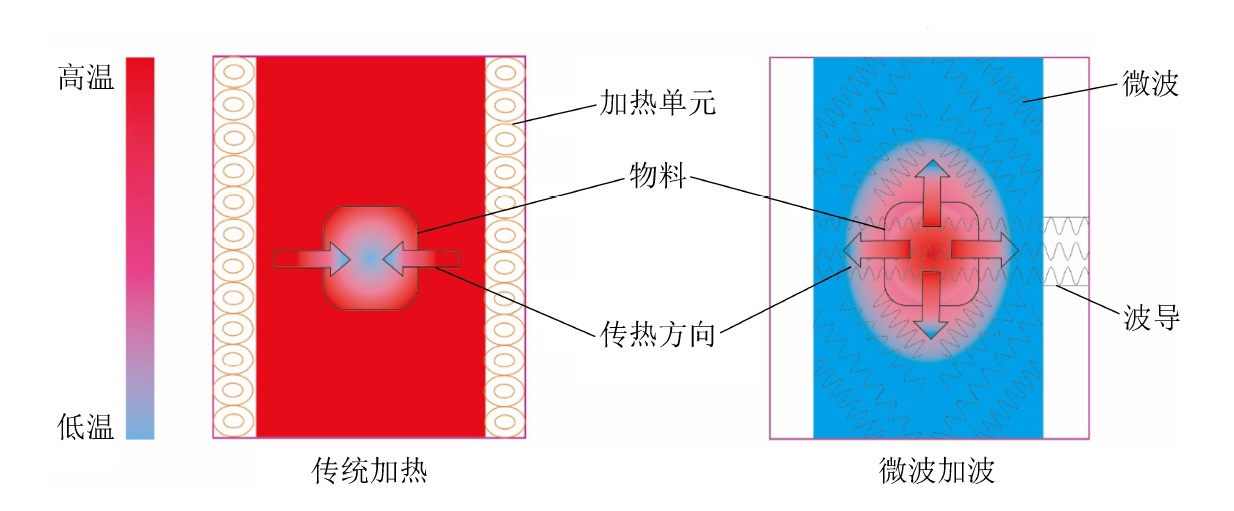
低阶煤微波辅助热提质研究进展

刘淑琴; 脱凯用

doi:10.13199/j.cnki.cst.2021.01.011

摘要: 微波热处理技术具有快速均匀、选择性加热和操作灵活、安全环保的优势，为实现低阶煤的清洁高效利用提供了新途径。从低阶煤的微波辅助干燥提质和热解提质出发，综述了低阶煤对微波的介电响应特性，梳理了影响低阶煤微波干燥提质过程的因素，阐述了微波干燥提质对低阶煤品质和理化性质的作用规律，不同工艺条件对低阶煤微波热解提质的影响以及引入吸波剂和催化剂对强化低阶煤微波热解提质的作用特性。结果表明：低阶煤中的水分和矿物含量是影响其介电损耗能力的主要因素，内在水分对微波的快速响应有利于实现微波对低阶煤的快速干燥提质。微波加热干燥有效提升了低阶煤固定碳含量和燃烧热值，内在水分被优先加热发生快速迁移可促进孔隙结构形成进而增强了其可磨性，极性含氧官能团在微波诱导下易发生分解有助于抑制低阶煤的自燃倾向。相比常规热解，微波辅助低阶煤热解提质表现出加热速率快、热解效率高、焦油轻质组分丰富以及合成气产量高的优势。微波功率、辐射时间、热解终温和反应气氛是影响低阶煤微波热解提质的主要因素，基于目标导向的热解工艺参数优化是实现低阶煤高效分级分质利用的核心。利用吸波剂和催化剂充分强化低阶煤微波热解提质，有利于提高微波能利用率、加深煤热解程度、定向调控产物分布以及改善热解产物品质。此外，微波辅助低阶煤和生物质、油页岩和废塑料等富氢物质进行共热解，能够增强焦油向轻质化的转变以及提升有效气体收率，是实现低阶煤清洁高效梯级利用的重要发展方向。

关键词:

Abstract: Microwave heating technology possesses the unique advantages of rapid and uniform heating, selective heating, flexible operation, safety and environmental protection, which offers a new way to achieve the clean and high-efficient utilization of low-rank coal. Based on the upgrading technology of microwave drying and pyrolysis of low-rank coal, the dielectric response characteristics of low-rank coal towards microwave were analyzed, and the factors influencing the microwave drying upgradation process of low-rank coal were summarized. Furthermore, the effect rules of microwave drying upgradation on the quality and physicochemical properties of low-rank coal were expounded, the impact of various process conditions on the microwave pyrolysis upgrading of low-rank coal are emphatically reviewed. Additionally, the characteristics of the introduction of microwave absorbers and catalysts on enhancing the microwave pyrolysis upgrading of low-rank coal are analyzed in detail. The results show that the moisture and mineral content of low-rank coal are the key factors of affecting its dielectric loss ability, and the rapid dielectric response of internal moisture towards microwave is beneficial to achieve the rapid drying and quality improvement of low-rank coal under microwave irradiation. Microwave drying can effectively improve the fixed carbon content and combustion calorific value of low- rank coal，and the internal moisture can be preferentially heated for rapid migration with microwave radiation, which is conducive to promoting the development of pore structure and the enhancement of grindability of low- rank coal. The oxygen-containing functional groups with polarity are easy to be decomposed under microwave induction, which is beneficial for inhibiting the spontaneous combustion of low-rank coal. Compared with conventional pyrolysis, microwave-assisted pyrolysis upgrading of low-rank coal shows numerous unique advantages involving fast heating rate, high pyrolysis efficiency, abundant light tar components, and high syngas production. Microwave power, radiation time, final pyrolysis temperature and reaction atmosphere are the main factors that affect the microwave pyrolysis process of low-rank coal. Target-oriented optimization of pyrolysis process parameters is the core for achieving the clean and high-efficient utilization of low-rank coal. The introduction of microwave absorbers and catalysts to fully strengthen the microwave pyrolysis process of low-rank coal is an effective way to increase the utilization rate of microwave energy, enhance the pyrolysis efficiency of coal, directional control of product distribution and improve the quality of pyrolysis products. In addition, microwave-assisted co-pyrolysis of low-rank coal and hydrogen-rich materials such as biomass, oil shale and waste plastics can enhance the production of light tar components and increase the yield the effective gas, which is the crucial development direction to realize the clean and high-efficient utilization of low-rank coal

Keywords:

0. 引　　言

煤炭是我国主体能源，在以实现“碳达峰”和“碳中和”为建设目标的能源转型中，其扮演着“压舱石”角色^[1-2]。伴随煤炭资源步入深部开采^[3-5]，地质构造更加复杂，煤层地压大、透气性差、瓦斯含量高，导致瓦斯动力灾害日趋严重。钻孔抽采技术^[6-8]是预防瓦斯动力灾害之重举，被广泛应用于诸多国内煤矿。然而现阶段主要依靠直径在0.042～0.130 m范围^[9-11]抽采孔，其单一钻孔有效抽采半径小、抽采量少、衰减快、抽采率低，需密集布置，造成工程量大成本高、预抽煤层达标慢接替紧张、瓦斯体积分数偏低难被利用等难题。

为改善钻孔抽采效果，国内研究人员开展了诸多钻孔增径手段如机械式扩孔^[12-13]、水力割缝^[14-18]、水力冲孔造穴^[19]等研究，即通过外界扰动煤层，人为促使煤体裂隙衍生、发育乃至贯通，缔造瓦斯流动通道，起到预抽区增透增流高效抽采目的。针对高突煤层实施上述手段可显著改善瓦斯钻孔抽采效果，有效预防瓦斯动力灾害。因此，深入剖析钻孔增径后煤体卸压增透机理有助于指导抽采孔优化。王亮等^[20]剖析了穿层钻孔造穴的增透机理，获得了渗透率分布规律。郝富昌等^[21]建立了钻孔黏弹塑性模型，得出水力冲孔扩径后煤体蠕变−瓦斯渗流演化规律。张福旺等^[22]通过现场实测瓦斯压力，得出密集水力冲孔下煤层瓦斯效果及运移规律，实现了煤层消突。贾传洋等^[23]借助室内尺寸效应试验和颗粒流仿真模拟手段剖析了不同参数下钻孔周边裂纹衍生发育形态及数目，得出了大直径钻孔卸压机理。秦贵成等^[24]分析了本煤层钻孔水力冲孔造穴前后有效抽采半径增效特征，并进行了现场验证。同时，也有一些学者针对瓦斯抽采钻孔影响因素如孔间距、孔径、负压等参数进行研究优化，亦满足了瓦斯抽采体积分数与抽采量提高的需求。潘俊锋等^[25]得出了不同孔间距下大直径钻孔卸压效能。李宏等^[26]剖析了大直径定向顶板长钻孔的层位、间距等参数对采空区瓦斯运移的影响，补充并完善了以孔代巷工艺。张春华等^[27]探究了大直径煤层钻孔周围的应力损伤破裂特征，得出了煤体透气性变化规律。陈月霞等^[28]采用理论分析与COMSOL数值模拟研究了抽采钻孔孔径与间距对瓦斯抽采的影响。程远平等^[29]建立了考虑基质瓦斯拟稳态扩散、裂隙瓦斯渗流、渗透率演化及煤体变形的瓦斯运移气固耦合模型，明确了负压对瓦斯抽采的作用机制。曹佐勇等^[30]分析了近距离突出煤层群水力冲孔钻孔周围煤体瓦斯压力与孔径之间的时空演化规律。

综上，聚焦于钻孔增径改造煤层取得了显著成效，对扰动煤体应力与变形规律、瓦斯分布规律有了一定认识，但仍存有不足——对钻孔增径后煤体长时力学效应下卸压增透瓦斯渗流演化机理研究较少。因此，为缓解高瓦斯低透气性煤层抽采难、治理难困境，以顺和煤矿2404典型深井高瓦斯低透气性煤层工作面为研究对象，深入剖析本煤层小直径钻孔优化为大直径钻孔后煤体卸压力学特征及渗透率变化规律，揭示钻孔增径后煤体长时力学效应下卸压增透瓦斯渗流演化机理，以期为相似地质矿井瓦斯灾害防治提供科学指导。

1. 长时力学效应下气固耦合模型

大直径钻孔在高应力软煤层开挖后如图1a所示，因围岩压力、瓦斯压力等条件改变，孔周煤体荷载被迫重分布，形成以孔为中心的“三区”——破碎区、塑性软化区和黏弹性区。如图1b所示，吸附瓦斯自煤体骨架表面解吸为游离瓦斯，游离瓦斯从基质孔隙扩散至裂隙，裂隙内的瓦斯通过渗流进入钻孔。软岩下钻孔周围煤体力学模型如图1c所示。其中，R_b(t)、R_p(t)分别为破碎区、塑性软化区半径，m；r₀为钻孔半径，m；σ₀为巷道开挖前的原地应力，MPa；σ_c为软岩体的单轴抗压峰值，MPa；σ_c^*为软岩体残余强度，MPa。$\sigma _r^i $、$\sigma _\theta ^i $分别为孔周的径向应力、孔周的切向应力，MPa。在破碎区、塑性软化区和黏弹性区i分别用“b”、“p”、“e”表示，下同。P_q(t)为支护抗力，MPa。α为煤内摩擦角，（°）；t为抽采时间，d。基于此模型研究高瓦斯煤层大直径钻孔卸压增透瓦斯渗流时空演化机理，充分考虑煤岩应力场、孔周裂隙场和瓦斯渗流场耦合所引起的煤体黏塑性变形对瓦斯扩散和渗流过程影响。基本假设如下：

图 1 气固耦合模型及对应的瓦斯运移过程

Figure 1. Physical model of coal containing gas and gas transport process

下载: 全尺寸图片幻灯片

①假设黏弹性区软岩变形服从蠕变模型Poyting-Thomson；②塑性软化区、破坏区煤体变形服从Mohr-Coulomb准则且均符合剪胀扩容特性，引入软岩变形时间效应；③假设煤体骨架不可压缩^[31-32]；④瓦斯视为理想气体，在煤层等温流动；⑤假设煤体为双重孔隙介质，蕴含诸多大量孔、裂隙；⑥瓦斯在压力梯度作用下沿煤层孔、裂隙作层流运动，符合达西渗流，同时考虑了Klikenberg效应。

1.1 煤体变形控制方程

孔周煤体变形问题常简化为轴对称平面应变问题，服从极坐标下平衡、几何方程^[33]：

$$ \left\{ \begin{gathered} \frac{{{\mathrm{d}}\sigma _r^i}}{{{\mathrm{d}}{\text{r}}}} + \frac{{\sigma _r^i - \sigma _{_\theta }^i}}{{{r}}} = 0 \\ \varepsilon _r^{{{{i}}}} = \frac{{{\mathrm{d}}{u^{_{{i}}}}}}{{{\mathrm{d}}{{r}}}} \\ \varepsilon _\theta ^{i} = \frac{{{u^{i}}}}{{{r}}} \\ \end{gathered} \right. $$

(1)

式中：$\varepsilon _r^{{{{i}}}} $、$ \varepsilon _\theta ^{{i}} $分别为孔的径向应变、孔的切向应变；uⁱ分别为破碎区、塑性软化区、黏弹性区的煤体位移量，m；r为极径。

1.1.1 黏弹性区的应力及应变

黏弹性区变形满足以下物性方程^[33]：

$$ \left\{\begin{array}{l} \sigma_r^{\mathrm{e}}-\sigma_0=2 G_{\infty} \varepsilon_r^{\mathrm{e}}+2 \xi_t G_{\infty} \dfrac{\mathrm{d} \varepsilon_r^{\mathrm{e}}}{\mathrm{~d} t} \\ \sigma_\theta^{\mathrm{e}}-\sigma_0=2 G_{\infty} \varepsilon_\theta^{\mathrm{e}}+2 \xi_t G_{\infty} \dfrac{\mathrm{d} \varepsilon_\theta^{\mathrm{e}}}{\mathrm{~d} t} \end{array}\right. $$

(2)

式中：$ \sigma _r^{\mathrm{e}} $、$ \sigma _\theta ^{\mathrm{e}} $分别为黏弹性区的径向应力和切向应力，MPa；ξ_t为煤岩延迟时间，d；G_∞为煤体长时的剪切模量，MPa。

黏弹性区体积应变为0，结合式（1）中第2、第3式有

$$\varepsilon_v^{\mathrm{e}}=\varepsilon_r^{\mathrm{e}}+\varepsilon_\theta^{\mathrm{e}}=\frac{\mathrm{d} u^i}{\mathrm{~d} r}+\frac{u^i}{r}=0 $$

(3)

粘弹−塑性区交界上，位移相等，由式（1）—式（3）得，黏弹性区位移及应力解为：

$$ \left\{\begin{array}{l} u^{\mathrm{e}}=\dfrac{B(t)^2}{4 r(t)} \\ \sigma_r^{\mathrm{e}}=\sigma_0-\dfrac{\Delta \sigma}{2} \dfrac{R_p(t)^2}{r^2} \\ \sigma_\theta^{\mathrm{e}}=\sigma_0+\dfrac{\Delta \sigma}{2} \dfrac{R_p(t)^2}{r^2} \end{array}\right. $$

(4)

其中，待定系数、弹塑性界面应力差可由下式求得：

$$ \left\{ \begin{array}{l} B(t)=\dfrac{\Delta \sigma R_{\mathrm{p}}(t)^2}{4} \times \\ {\left\{\dfrac{1}{G_{\infty}}\left[1-\exp \left(-\dfrac{t}{\xi_t}\right)\right]+\dfrac{1}{G_0} \exp \left(-\dfrac{t}{\xi_t}\right)\right\}} \\ \Delta \sigma=2 \sigma_0 \sin\; \alpha+2 C \cos\; \alpha \\ R_p(t)=r_0\left[\dfrac{\left(\sigma_0+C \operatorname{ctan} \alpha\right)(1-\sin\; \alpha)}{P_q(t)+C \operatorname{ctan} \alpha}\right]^{\tfrac{1-\sin\; \alpha}{2 \sin\; \alpha}} \\ P_q(t)=-C \operatorname{ctan} \alpha+\left(\sigma_0+C \operatorname{ctan} \alpha\right) \times \\ (1-\sin\; \alpha)\left(\dfrac{\Delta \sigma r_0}{4 G_0 u(t)}\right)^{\tfrac{\sin\; \alpha}{1-\sin\; \alpha}} \\ u(t)=\left(u-u_0\right)[1-\exp (-q t)]+u_0 \end{array}\right. $$

(5)

式中：u^e为黏弹性区的煤体位移量，m；B(t)为时间函数，m；G₀为煤体初始的剪切模量，MPa。Δσ为黏弹−塑性界面上应力差，MPa；C为煤体黏聚力，MPa；$ u(t) $为孔壁随时间而变的位移变化量，m；u₀为初始孔壁位移变化量，m；$ {u} $为围岩变形稳定时孔壁总位移变化量，m；q为钻孔支护系数，取1.5。

1.1.2 塑性软化区的应力及应变

塑性软化区的煤体变形存有软化及扩容现象，有以下方程^[33]：

$$ \Delta \varepsilon_r^{\mathrm{p}}+\eta_1 \Delta \varepsilon_\theta^{\mathrm{p}}=0 $$

(6)

式中：$\Delta \varepsilon_r^{\mathrm{p}}$、$\Delta \varepsilon_\theta^{\mathrm{p}} $为塑性软化区的径向、切向应变的增量，MPa；塑性软化区的软化系数η₁=(1+sin β)/(1−sin β)，β为煤体膨胀角，（°）。

塑性软化区应变为

$$ \left\{\begin{array}{l} \varepsilon_r^{\mathrm{p}}=\left(\varepsilon_r^{\mathrm{e}}\right)_{r=R_{\mathrm{p}}(t)}+\Delta \varepsilon_r^{\mathrm{p}} \\ \varepsilon_\theta^{\mathrm{p}}=\left(\varepsilon_\theta^{\mathrm{e}}\right)_{r=R_{\mathrm{p}}(t)}+\Delta \varepsilon_\theta^{\mathrm{p}} \end{array}\right. $$

(7)

由式（1）、（2）、（6）和（7）可得，塑性区位移、应变为：

$$ \begin{aligned} & u^{\mathrm{p}}=\frac{\eta_1-1}{\eta_1+1} \frac{B(t) r}{R_{\mathrm{p}}(t)^2}+\frac{2 B(t)}{\eta_1+1} \frac{R_{\mathrm{p}}(t)^{\eta_1-1}}{r^{\eta_1}} \\ & \varepsilon_v^{\mathrm{p}}=2 B(t) \frac{\eta_1-1}{\eta_1+1} \left(\frac{1}{R_{\mathrm{p}}(t)^2}-\frac{R_{\mathrm{p}}(t)^{\eta_1-1}}{r^{\eta_1+1}}\right) \end{aligned}$$

(8)

塑性软化区应力解可采用文献[34]得到：

$$ \left\{ \begin{aligned} & \sigma_\theta^{\mathrm{p}}=N \left(\frac{1+\sin \alpha}{1-\sin \alpha}\right)\left(\frac{r}{r_0}\right)^{\tfrac{2 \sin \;\alpha}{1-\sin \;\alpha}}-C \operatorname{ctan} \alpha \\ & \sigma_r^{\mathrm{p}}=N \left(\frac{r}{r_0}\right)^{\tfrac{2 \sin \alpha}{1-\sin \alpha}}-C \operatorname{ctan} \alpha \\ & N=K_{\mathrm{c}}\left(\frac{B(t)}{r_0}-u_0\right)+C \operatorname{ctan} \alpha \end{aligned}\right. $$

(9)

式中：K_c=(1+sin α)/(1−sin α)。

1.1.3 破坏区

破坏区煤体的变形存有扩容现象，有：

$$ \Delta \varepsilon_r^b+\eta_2 \Delta \varepsilon_\theta^b=0$$

(10)

式中：$ \Delta \varepsilon_r^b$、$ \varepsilon_\theta^b$为破坏区径向和切向应变增量，MPa；η₂为扩容系数，通常取1.1～1.3。

破坏区应变为

$$ \left\{\begin{array}{l} \varepsilon_r^{\mathrm{b}}=\left(\varepsilon_r^{\mathrm{p}}\right)_{r=R_{\mathrm{b}}(t)}+\Delta \varepsilon_r^{\mathrm{b}} \\ \varepsilon_\theta^{\mathrm{b}}=\left(\varepsilon_\theta^{\mathrm{p}}\right)_{r=R_{\mathrm{b}}(t)}+\Delta \varepsilon_\theta^{\mathrm{b}} \end{array}\right. $$

(11)

联立式（1）、（10）、和（11）得，破坏区位移解、应变为：

$$\begin{gathered} u^{\mathrm{b}}=\frac{\left(\eta_2-\eta_1\right)}{\eta_2+1} \frac{2 B(t)}{\eta_1+1} \frac{R_{\mathrm{p}}(t)^{\eta_1-1}}{R_{\mathrm{b}}(t)^{\eta_1+1}} r+ \\ \left[\frac{2 B(t)}{\eta_2+1} \frac{R_{\mathrm{p}}(t)^{\eta_1-1}}{R_{\mathrm{b}}(t)^{\eta_1-\eta_2}}\right] r^{-\eta_2}+\frac{\eta_1-1}{\eta_1+1} \frac{B(t)}{R_{\mathrm{p}}(t)^2} r \end{gathered}$$

(12)

$$ \begin{gathered} \varepsilon_v^{\mathrm{b}}=\frac{\left(\eta_2-\eta_1\right)}{\eta_2+1} \frac{4 B(t)}{\eta_1+1} \frac{R_{\mathrm{p}}(t)^{\eta_1-1}}{R_{\mathrm{b}}(t)^{\eta_1+1}}+ \\ \frac{\left(1-\eta_2\right) 2 B(t)}{\eta_2+1} \left(\frac{R_{\mathrm{p}}(t)^{\eta_1-1}}{R_{\mathrm{b}}(t)^{\eta_1-\eta_2}}\right) r^{-\eta_2-1}+\frac{\eta_1-1}{\eta_1+1} \frac{2 B(t)}{R_{\mathrm{p}}(t)^2} \end{gathered}$$

(13)

破坏区应力解可采用弹塑性力学得到：

$$ \left\{ \begin{gathered} \sigma _r^{\mathrm{b}}{\text{ = }}\frac{{{{\left( {Jr} \right)}^{{K_{\mathrm{c}}} - 1}} - \sigma _{\mathrm{c}}^*}}{{\left( {{K_{\mathrm{c}}} - 1} \right)}} \\ \sigma _\theta ^{\mathrm{b}} = {K_{\mathrm{c}}}\sigma _r^{\mathrm{b}} + \sigma _{\mathrm{c}}^* \\ \end{gathered} \right. $$

(14)

其中，破坏区半径为：

$$R_{\mathrm{b}}(t)=r_0\left(\frac{\sigma_{\mathrm{c}}^*-\left(K_{\mathrm{c}}-1\right) J \operatorname{ctan} \alpha}{\sigma_{\mathrm{c}}^*+\left(K_{\mathrm{c}}-1\right)\left(P_{\mathrm{q}}(t)-N-J \operatorname{ctan} \alpha\right)}\right)^{\tfrac{1}{K_{\mathrm{c}}-1}} $$

(15)

$$ J=\frac{1}{R_{\mathrm{b}}(t)}\left\{\left(K_{\mathrm{c}}-1\right)\left[N \left(\frac{R_{\mathrm{b}}(t)}{r_o}\right)^{\tfrac{2 \sin\; \alpha}{1-\sin \;\alpha}}-C \operatorname{ctg} \alpha\right]+\sigma_{\mathrm{c}}^*\right\}^{\tfrac{1}{K_{\mathrm{c}}-1}} $$

(16)

定量探究扩孔扰动下煤体“三区”分布的影响。普通煤层瓦斯抽采钻孔为75 mm，扩孔直径分取100、200 和300 mm。时间域取0～180 d，利用Matlab软件将三者塑性软化区、破坏区半径绘制成相应时演曲线如图2所示。

图 2 破坏区和塑性区变化

Figure 2. Development range of failure zone and plastic zone

下载: 全尺寸图片幻灯片

由图2可知，时间一定时，自图底部向顶部看，随着钻孔孔径增大，塑性软化区、破坏区半径均明显增加。时间为 6 d 孔径由 100 mm 增至 200、300和400 mm时，钻孔塑性软化区半径由 0.29 m 增至 0.58、0.87和0.88 m，分别增加了 0.29、0.58 和0.59 m；破坏区半径由 0.17 m 增至 0.33、0.49、0.45 m，分别增加了 0.16、0.32 和0.28 m。由前人研究^[35]可知钻孔卸压区往往是其塑性软化区边界，这表明增大钻孔孔径有利于钻孔周边卸压区扩展。随着孔径增大，塑性软化区增幅大于破坏区。孔径一定时，自图左向右看，随着时间增加，塑性软化区、破坏区半径逐步增加而后增幅减缓，终趋于稳定，时间为0～6 d，300 mm钻孔塑性软化区、破坏区半径由0.15 m增至0.87、0.49 m，而后6～180 d时，二者大小分别保持在0.87、0.49 m左右。

煤层瓦斯压力由初始值p₀降到p时，瓦斯压力变化导致的煤基质收缩体应变量ε_m为^[36]：

$$ {\varepsilon _{\mathrm{m}}} = \frac{{2a{\rho _{{\mathrm{coal}}}}RT\left( {1 - 2{\text{v}}} \right){\mathrm{ln}}\left( {\dfrac{{1 + b{p_{{\mathrm{m}}0}}}}{{1 + b{p_{\mathrm{m}}}}}} \right)}}{{3{E_{\mathrm{m}}}V}} $$

(17)

式中：ρ_coal为煤密度，kg/m³；R为理想气体常数，kg/(kmol·K)；T为绝对温度，K；v为煤体的泊松比；V为气体摩尔体积，取22.4 L/mol；E_m为煤基质弹性模量，MPa； p_m0为煤基质初始瓦斯压力等于煤层瓦斯压力初始值p₀，MPa；p_m为煤基质瓦斯压力等于煤层瓦斯压力p，MPa。

综上，“三区”煤体变形场控制方程^[37]为

$$\left\{\begin{array}{l} G_{\mathrm{t}} u_{j, k l}^i+\dfrac{G_{\mathrm{t}}}{1-2 v} u_{k, j l}^i-\gamma p_{\mathrm{m}}-K_{{\mathrm{c o}}} \varepsilon_{\mathrm{m}}+F_i=0 \\ G_{\mathrm{t}}=\dfrac{1}{G_{\infty}}\left(1-\mathrm{e}^{-\tfrac{t}{\xi_{\mathrm{t}}}}\right)+\dfrac{1}{G_0} \mathrm{e}^{-\tfrac{t}{\xi_{\mathrm{t}}}} \end{array}\right. $$

(18)

$$ {\varepsilon _{\mathrm{c}}} = \frac{{{\sigma _{jk{\text{l}}}} - {\sigma _0} - \gamma \left( {{{{p}}_m} - {{{p}}_{m 0}}} \right)}}{{{K_{{\text{co}}}}}} $$

(19)

式中：G_t为动态的煤体剪切模量，MPa；$ {\boldsymbol{u}}_{j,kl}^{i} $为位移张量形式，m，且第1个下标j表示$ {\boldsymbol{u}}^{i} $的j方向分量，第2个下标k表示对$ {\boldsymbol{u}}_{{j}}^{i} $求k方向偏导数，第3个下标l表示对$ {\boldsymbol{u}}_{k,j}^{^i} $求k方向偏导数；γ为Biot系数，γ=1−K_co/K_m，其中K_co为煤体的体积模量，MPa，满足K_co=E_c/3(1−2v)，E_c为煤体弹性模量，MPa，K_m为煤基质的体积模量，MPa，K_m=E_m/3(1−2v)；ε_m为煤基质孔隙紧缩时体应变量；F_j为体积力，MPa；ε_c为有效应力变化的应变量；σ_jkl为“三区”的应力张量形式，MPa。

1.2 煤层瓦斯渗流控制方程

单一煤层无质量源时，煤体瓦斯流动方程为

$$ \frac{{\partial Q}}{{\partial t}} + \nabla \cdot \left( {{\rho _{\text{g}}} \cdot {{{q}}_{{c}}}} \right) = 0 $$

(20)

式中：ρ_g为瓦斯密度，kg/m³；q_c为瓦斯渗流速度，m/s；Q为单位体积含瓦斯煤岩中瓦斯含量，kg/m³。Q由2部分组成：①基质和裂隙中游离态瓦斯含量Q_a，kg/m³；②煤体骨架吸附态瓦斯含量Q_b，kg/m³，故

$$ \frac{\partial Q}{\partial t}=\frac{\partial Q_{\mathrm{a}}}{\partial t}+\frac{\partial Q_{\mathrm{b}}}{\partial t} $$

(21)

瓦斯密度及压力遵循式(22)：

$$ \frac{{\partial {Q_{\text{a}}}}}{{\partial t}} = \frac{{{S_{\mathrm{g}}}}}{{RT}}\left( {p\frac{{\partial \varphi }}{{\partial t}} + \varphi \frac{{\partial p}}{{\partial t}}} \right) $$

(22)

式中：S_g为瓦斯的分子量，g/mol；φ为含瓦斯煤岩动态孔隙率，m²。

单位体积的煤中考虑水分、灰分的煤体骨架吸附态瓦斯含量为

$$ Q_{\mathrm{b}}=\frac{a b c p \rho_{\mathrm{n}}}{1+b p} $$

(23)

$$ c={{\rho }_{{\mathrm{coal}}}} \frac{1-A-{{O}_{{\mathrm{ad}}}}}{1+0.31{{O}_{{\mathrm{ad}}}}} $$

(24)

式中：a为单位质量煤所测的最大吸附瓦斯量，m³/kg；b为单位质量煤所测的煤的吸附常数，MPa⁻¹；c为煤的校正参数，kg/m³；A为灰分；O_ad为水分；ρ_n为常压下瓦斯密度，kg/m³。

$$ \frac{\partial Q_{\mathrm{b}}}{\partial t}=\frac{a b c \rho_{\mathrm{n}}}{(1+b p)^2} \frac{\partial p}{\partial t} $$

(25)

煤层瓦斯渗流速度为

$$ {{{q}}_c} = - \frac{{k\left( t \right)}}{\mu }\left( {\nabla {\text{p}} + {\rho _g}g\nabla {\textit{z}}} \right) $$

(26)

式中：k(t)为动态变化的渗透率，m²；μ为瓦斯动力黏度系数，Pa·s；g为重力加速度，m/s²；$ \nabla _{\textit{z}} $=（0，0，1）。

由式（20）—式（26）得煤层瓦斯渗流控制方程为：

$$ \begin{gathered} \frac{{{\text{abc}}{\rho _n}}}{{{{\left( {1 + bp} \right)}^2}}}\frac{{\partial p}}{{\partial t}} + \frac{{{S_{\mathrm{g}}}}}{{RT}}\left( {p\frac{{\partial \varphi }}{{\partial t}} + \varphi \frac{{\partial p}}{{\partial t}}} \right)+ \\ \nabla \cdot \left[ { - p\frac{{k\left( t \right){S_g}}}{{\mu RT}}\left( {\nabla {\text{p}} + {\rho _g}g\nabla {\textit{z}}} \right)} \right] = 0 \\ \end{gathered} $$

(27)

由方程（27）知，只要给出动态变化的渗透率k(t)和含瓦斯煤岩动态孔隙率φ就可进行求解。

1.3 孔隙率和渗透率动态变化模型

孔隙率和渗透率决定了卸压瓦斯沿着煤层−孔裂隙−钻孔路径运移的难易程度。根据孔隙率φ定义^[38]，动态变化的孔隙率φ为

$$ \varphi=1-\frac{1-\varphi_0}{1+\varepsilon_v}\left(1+\varepsilon_{\mathrm{m}}+\varepsilon_{\mathrm{c}}\right) $$

(28)

受应力变化和瓦斯解吸的影响，煤层渗透率处于动态变化中。根据Carman-Kozeny经验公式，得“三区”渗透率方程为

$$ k\left( t \right) = \frac{{{k_0}}}{{1 + \varepsilon _v^{}}}{\left[ {1 + \frac{{\varepsilon _v^{} + {\varepsilon _{\mathrm{m}}} + \varepsilon _{\mathrm{c}}^{}}}{{{\varphi _0}}}} \right]^3} $$

(29)

$$ \varepsilon_v=\left\{\begin{array}{l} \text { 破裂区 } r \leqslant R_{\mathrm{b}}(t) \\ \varepsilon_v^{\mathrm{b}}=\dfrac{\left(\eta_3-\eta_2\right)}{\eta_3+1} \dfrac{4 B(t)}{\eta_2+1} \dfrac{R_{\mathrm{p}}(t)^{\eta_2-1}}{R_{\mathrm{b}}(t)^{\eta_2+1}}+ \dfrac{\left(1-\eta_3\right) 2 B(t)}{\eta_3+1} \times \\ \left(\dfrac{R_{\mathrm{p}}(t)^{\eta_2-1}}{R_{\mathrm{b}}(t)^{\eta_2-\eta_3}}\right) r^{-\eta_3-1}+ \dfrac{\eta_2-1}{\eta_2+1} \dfrac{2 B(t)}{R_{\mathrm{p}}(t)^2} \\ \text { 塑性软化区 } R_{\mathrm{b}}(t) \leqslant r \leqslant R_{\mathrm{p}}(t) \\ \varepsilon_v^{\mathrm{p}}=2 B(t)\times \dfrac{\eta_2-1}{\eta_2+1} \left(\dfrac{1}{R_{\mathrm{p}}(t)^2}-\dfrac{R_{\mathrm{p}}(t)^{\eta_2-1}}{r^{\eta_2+1}}\right) \\ \text { 黏弹性区 } r \geqslant R_{\mathrm{p}}(t) \\ \varepsilon_v^{\mathrm{e}}=0 \end{array}\right. $$

(30)

图3为0.30 m钻孔渗透率与抽采时间和瓦斯压力分布。前文研究可知，100、200、300 mm大直径钻孔塑性软化区、破坏区半径时演曲线均在6 d达到拐点，故抽采时间t取6 d，瓦斯压力取0.50～0.58 MPa，具有一定典型性。由图可知，抽采瓦斯压力一定，渗透率随抽采时间t增加而增大，时间变化越快渗透率增长速度越快，意味着塑性软化区、破坏区增加有利于大直径钻孔对煤层增透。抽采时间一定，孔周渗透率随瓦斯压力衰降而逐步增大，瓦斯压力梯度下降越明显渗透率增值越大，意味着大直径钻孔对煤层增透效果越好。

图 3 300 mm钻孔渗透率、抽采时间和瓦斯压力分布

Figure 3. Permeability, extraction time, gas pressure distribution of 300 mm boreholes

下载: 全尺寸图片幻灯片

2. 钻孔卸压增透机理模拟分析

河南永煤集团顺和煤矿为突出矿井，2404工作面位于顺和煤矿24采区，主采二₂煤，埋深为−520～−750 m，均厚为3.0 m。煤层透气性为0.46 m²/(MPa²·d)，实测原始瓦斯含量为2.06～11.21 m³/t，原始瓦斯压力实测值为0.58 MPa，煤体密度1.50 t/m³。瓦斯放散初速度平均值为13.5～22.6 mmHg。煤层埋深大、地压大、瓦斯含量高、透气性低，实乃典型深井高瓦斯低透气性中厚煤层，瓦斯治理存在钻孔抽采有效期短、纯量偏低难利用等难题，导致工作面采掘接替紧张，严重制约了矿井高效高产，采用如今的瓦斯抽采治理技术体系未能实现预期效果。为走出高瓦斯低透气性煤层治理难困境，提高抽采效率，实现煤层快速消突，该工作面准备采用大直径煤层瓦斯抽采钻孔对二₂煤层进行卸压增透。

为研究孔径对煤层卸压增透效果的影响强弱，建立图4的单孔卸压强化瓦斯抽采几何模型。在高瓦斯低透气性中厚煤层里布置1根半径r₀钻孔，孔径分别取50、100、150、200 mm，共计4种方案。模型长为20 m，高为10.0 m，顶、底板厚度各为5.0、2.0 m，煤厚3.0 m。

图 4 单孔卸压增透几何模型

Figure 4. Geometry of single-hole pressure reduction and reflection enhancement

下载: 全尺寸图片幻灯片

沿二₂煤层中线布置1条测线。顶部恒定地应力18.0 MPa（模拟埋深750 m），底部属于固定的边界，两侧划定为辊支边界。煤层初始瓦斯压力设为0.58 MPa，四廓设为零流量边界，孔周为0.087 MPa模拟13 kPa抽采负压，模型输入参数见表1。

表 1 模型输入参数

Table 1. Parameter input in the model

参数	取值	参数	取值
瓦斯含量/（m³·t⁻¹）	11.21	煤基质弹性模量E_m/MPa	8400
初始瓦斯压力p₀/MPa	0.58	煤体弹性模量E/MPa	6420
最大吸附量a/(m³·t⁻¹)	46.12	煤层初始孔隙率φ₀	0.037
最大吸附常数b/MPa⁻¹	1.42	煤层初始渗透率k₀/m²	1.15×10⁻¹⁷
煤黏聚力C/MPa	0.20	标况瓦斯密度ρ_n/（kg·m⁻³）	0.717
煤内摩擦角α/（°）	30	煤层温度T/K	293
煤体膨胀角β/（°）	10	气体质量S_g/（kg·kmol⁻¹）	0.016
煤密度ρ_c/（kg·m⁻³）	1500	灰分A/%	15.22
残余强度σ_c^*/MPa	2.0	水分O_ad/%	2.74
瓦斯动力黏度μ/（Pa·s）	1.84×10⁻⁵	理想气体常数R/( kg·(kmol·K)⁻¹⁾	8.4135
泥岩泊松比	0.29	泥岩渗透率/m²	3×10⁻²¹

下载: 导出CSV

| 显示表格

2.1 单孔有效抽采半径影响分析

钻孔有效抽采半径是顺层瓦斯抽采钻孔重要指标^[39-40]，直接关乎后续瓦斯抽采钻孔间距的确定。根据《防治煤与瓦斯突出细则》及矿井所属省份《河南省煤矿防治煤与瓦斯突出十项措施》相关要求：顺和煤矿2404工作面抽采有效半径判定指标为瓦斯预抽率达到30%，即层内瓦斯的含量由原始含量11.21 m³/t降至残余含量3.37 m³/t，采用修正的朗格缪尔方程计算得出煤层残余瓦斯压力为0.22 MPa，故本文模拟将瓦斯压力降至0.22 MPa以内区域划分为抽采达标区域。为确定合理钻孔半径r₀及孔间距L，利用COMSOL软件分别模拟100、200、300和400 mm单孔瓦斯抽采180 d过程，瓦斯压力分布如图5所示，红色所圈区域为抽采达标区域。

图 5 钻孔周围瓦斯压力分布

Figure 5. Gas pressure distribution around drilling holes

下载: 全尺寸图片幻灯片

可以看出，经过一定时间的抽采后，煤层瓦斯压力呈以钻孔中心为对称中心的椭圆分布，由钻孔向外逐渐增加，随抽采时间增加，抽采达标区域逐渐扩大。300 mm钻孔抽采2 d后有效抽采半径达到0.28 m，抽采30 d后有效抽采半径达到0.50 m，抽采180 d后有效抽采半径达到1.32 m。在煤层瓦斯预抽采后期，随着抽采时间的延长，有效抽采半径虽还在缓慢增大，但其变化幅度越来越小，趋于稳定。抽采时间一定时，瓦斯抽采达标区域随钻孔孔径增大而增宽，增量不变是瓦斯抽采达标区随孔径增大而增长变缓慢。100、200、300、400 mm钻孔抽采180 d有效抽采半径分别为0.75、1.02、1.30和1.36 m。由此可见，不同模拟方案的煤层瓦斯压力分布和有效抽采半径结果差异明显。为探明增径差异性需分析大直径钻孔卸压力学特征。

2.2 大直径钻孔卸压力学特征

大直径钻孔卸压效果的评价以钻孔周边应力转移效果作为指标。不同孔径大直径钻孔围岩垂直应力随抽采时间变化如图6所示。不同孔径条件下，大直径钻孔围岩垂直应力呈对称分布，其左右两侧均会形成应力集中区。孔径一定时，随抽采时间增加，应力集中区呈现先增后减趋势。100 mm钻孔抽采时间由2 d增至30 d，应力集中区长度由0.50 m增至0.80 m，增幅达60%；而后由30 d增至180 d，其应力集中区水平长度由0.80 m减至0.60 m，减幅为25%。这意味着钻孔开挖后围岩应力失衡造成应力集中，应力集中区增大，而负压抽采一段时间后由于煤岩卸压瓦斯流动后再次平衡，进而应力集中区减小。而抽采时间一定时，随着孔径增大，应力集中区呈现逐步增大趋势。当抽采时间t=2 d时，孔径由100 mm增大到200、300、400 mm，应力集中区水平长度对应增加了0.48、0.60、1.10 m，增幅分别高达96%、120%、220%。

图 6 大直径钻孔围岩垂直应力随抽采时间变化云图

Figure 6. Vertical stress over time plot of surrounding rock in large diameter boreholes

下载: 全尺寸图片幻灯片

为进一步分析钻孔周边应力转移特征，沿Y=3.50 m在4种大直径钻孔左侧1.00 m内提取5个点（分别是X=9.61、9.67、9.73、9.77和9.79 m），其垂直应力随时间变化如图7所示。

图 7 大直径钻孔周围点的垂直应力随时间变化曲线

Figure 7. Vertical stress over time plot at points around large diameter boreholes

下载: 全尺寸图片幻灯片

钻孔周边应力转移特征为：随抽采时间增加，单钻孔周边点的垂直应力呈现先升后降趋势，于抽采时间t=7d时达到峰值。自下而上看，与钻孔中心（X=10.00 m）距离越远点，垂直应力峰值越大。如图8a所示，抽采时间从0到7 d，100 mm钻孔左侧5点（X=9.61、9.67、9.73、9.77、9.84 m）垂直应力分别由初始值11.4、11.4、11.4、12.8、12.8 MPa，增至峰值20.4、21.1、21.9、22.5、24.6 MPa，平均增幅近100%。到180 d时，垂直应力降至19.1、19.6、20.2、20.6、22.1 MPa，降低了1.3、1.5、1.7、1.9、2.5 MPa，垂直应力降低幅度趋于平缓，但垂直应力最终值仍高于初值。这表明大直径钻孔开挖后7 d内，其周边煤岩趋于应力平衡，是大直径钻孔的重点养护期，应采取相应技术来提升钻孔周边煤岩支护强度，维护完整性，避免钻孔因煤壁过于破碎出现漏气或塌孔现象导致钻孔抽采瓦斯效果不佳。

图 8 单一大直径钻孔渗透率沿煤层走向分布规律

Figure 8. Distribution of single-large diameter boreholes permeability along coal seam

下载: 全尺寸图片幻灯片

2.3 单孔渗透率时空演化特征

顺层大直径钻孔增透效果评价指标为抽采区域渗透率的变化。沿Y=3.50 m线分别提取抽采180 d时3种大直径钻孔模型两侧3.00 m内渗透率数据进行对比分析。图8为单一大直径钻孔渗透率沿煤层走向的分布规律。整体上，单一钻孔周边渗透率变化以大直径钻孔为中心呈对称分布规律，即自钻孔中心向两侧，煤层渗透率出现不同程度降低，距钻孔中心越远，渗透率变化越小，并逐渐趋于稳定。追溯其原因，钻孔稳定负压长时抽采时，离孔中心越近，其瓦斯压力衰减越快，瓦斯更易解吸流向孔内，煤基质收缩效应较煤体骨架压缩效应更为明显，导致渗透率在孔周变幅更急剧，这与图3中渗透率随抽采时间的变化规律是相似的。煤层初始渗透率为1.15×10⁻¹⁷ m²，抽采180 d后，100 mm钻孔渗透率介于1.50×10⁻¹⁶ ～3.20×10⁻¹⁵ m²，平均渗透率为6.04×10⁻¹⁶ m²；抽采180 d后，200 mm钻孔渗透率介于1.50×10⁻¹⁶ ～3.21×10⁻¹⁵ m²，平均渗透率为8.09×10⁻¹⁶ m²；300 mm钻孔渗透率介于2.50×10⁻¹⁶ ～3.56×10⁻¹⁵ m²，平均渗透率为1.12×10⁻¹⁵ m²；400 mm钻孔渗透率介于3.10×10⁻¹⁶ ～3.52×10⁻¹⁵ m²，平均渗透率为1.15×10⁻¹⁵ m²。综上，孔径增大能取得较好增透效果，通过模拟确定孔径300 mm较佳。此外，考虑到钻孔施工维护难易程度，大直径钻孔的设计直径应结合钻机设备及施工条件综合确定。

2.4 多孔瓦斯压力和渗透率分布规律

为了考虑不同钻孔间的叠加效应，建立卸压强化瓦斯抽采的几何模型如图9所示。模型长20 m，高10 m，顶、底板厚度各为5、2 m，煤厚为3 m，模型内设3个300 mm大直径钻孔，孔间距为L。沿Y=3.50 m布置一条测线。顶部恒定地应力18.0 MPa（模拟埋深750 m），底部属于固定的边界，两侧划定为辊支边界。煤层初始瓦斯压力设为0.58 MPa，四廓设为零流量边界，孔周为0.087 MPa模拟13 kPa抽采负压，模型输入参数见表1。

图 9 几何模型示意

Figure 9. Geometric schematic

下载: 全尺寸图片幻灯片

利用COMSOL分别模拟孔径300 mm孔间距L为4.0、6.0和8.0 m多孔下瓦斯抽采180 d全过程。多孔抽采瓦斯时煤层瓦斯压力分布规律如图11所示。整体上，多钻孔周边瓦斯压力变化以中心孔圆心为对称中心呈对称分布规律，即在多孔抽采叠加效应作用下，两孔中心地带的瓦斯压力明显低于孔另一侧等距离处的瓦斯压力。

图 11 多钻孔抽采时瓦斯压力和渗透率分布曲线

Figure 11. Gas pressure and permeability distribution curves during multi-borehole extraction

下载: 全尺寸图片幻灯片

当孔间距L为4.0 m时，如图10a所示，300 mm钻孔a、b、c三孔周边瓦斯压力呈现出“两小一大”的分布，即钻孔b两侧钻孔0.09 MPa以内瓦斯压力分布呈偏心圆，当然，在三孔合力下，5.0～15.0 m以内煤层瓦斯压力均在0.19 MPa以内，故抽采达标。当孔间距为6.0 m时，如图10b所示，300 mm钻孔a、b、c三孔周边瓦斯压力呈现出“三个均匀圆”分布，即三孔在0.10 MPa以内瓦斯压力呈等圆分布，钻孔b两侧钻孔0.09 MPa以内瓦斯压力分布呈偏心圆，背离钻孔b。当然，在三孔合力下，2.0～18.0 m以内煤层瓦斯压力均在0.22 MPa以内，故抽采达标范围更大更广。当孔间距为8.0 m时，如图10c所示，300 mm钻孔a、b、c三孔周边瓦斯压力呈现出“两大一小”的分布，即瓦斯压力0.11 MPa以内钻孔b最小，两侧钻孔0.11 MPa以内瓦斯压力分布呈偏心圆，但重心偏离钻孔b，这是由于孔间距过大，存在瓦斯压力积聚带，即 4.0～8.0 m内煤层瓦斯压力部分高达0.27 MPa，故0～20.0 m区域钻孔瓦斯抽采不达标。

图 10 多孔抽采180 d时瓦斯压力分布

Figure 10. Gas pressure distribution during porous extraction for 180 d

下载: 全尺寸图片幻灯片

为精准分析多孔抽采下瓦斯变化规律，分别提取3种大直径钻孔（抽采180 d）围岩瓦斯压力和渗透率进行对比，如图11所示。由图11a可知：多钻孔抽采瓦斯时，相邻两钻孔中心瓦斯压力变化呈“M”型分布，孔间距越大，M开口越大，多孔抽采控制区域更广。但抽采达标区域不会随孔间距增大而增大，因为M的峰值也会随孔间距增大而增高且峰值所处位置也会更远离中心钻孔，导致更容易形成瓦斯积聚带。以残余瓦斯压力0.22 MPa为临界值，可得300 mm孔径多孔抽采孔间距6.0 m的达标区域最广，故其瓦斯抽采效果最佳。

孔间距4.0 m多孔抽采180 d时，中心孔两侧4.0 m内的瓦斯压力均不超过0.12 MPa，远小于单孔抽采瓦斯时中心孔两侧3.0 m内的瓦斯压力最大值0.35 MPa，且相比于单孔抽采时下降了65.7%。孔间距6.0 m多孔抽采180 d时，中心孔两侧6.0 m内的瓦斯压力均不超过0.21 MPa，远小于单孔抽采瓦斯时中心孔两侧3.0 m内的瓦斯压力最大值0.35 MPa，且相比于单孔抽采时下降了40.0%。孔间距8.0 m多孔抽采180 d时，中心孔两侧8.0 m内的瓦斯压力均不超过0.30 MPa，也小于单孔抽采瓦斯时中心孔两侧3.0 m内的瓦斯压力最大值0.35 MPa，且相比于单孔抽采时下降了16.7%。这表明顺层多钻孔抽采瓦斯时，在抽采叠加效应的影响下，距钻孔不同距离处煤层瓦斯压力降幅比单钻孔抽采时更大。煤层初始渗透率为1.15×10⁻¹⁷ m²，300 mm单孔平均渗透率为1.12×10⁻¹⁵ m²，由图11b可知，抽采180 d后，孔间距4.0 m钻孔渗透率介于1.60×10⁻¹⁶ ～3.21×10⁻¹⁶ m²，平均渗透率为1.35×10⁻¹⁵ m²；孔间距6.0 m渗透率介于4.60×10⁻¹⁶ ～3.57×10⁻¹⁵ m²，平均渗透率为1.58×10⁻¹⁵ m²；孔间距8.0 m渗透率介于4.60×10⁻¹⁶ ～3.58×10⁻¹⁵ m²，平均渗透率为1.53×10⁻¹⁵ m²。综上，孔径取300 mm、孔间距取4.0～6.0 m时，煤层大直径抽采钻孔可取得较佳增透效果。

3. 现场应用

试验地点为2404工作面运输巷道，如图12所示。以180 d作为预期抽采达标时间确定出对应的大直径钻孔间距为6.0 m，考虑到瓦斯压力和含量均低于临界值可增大孔间距至8.0 m。在2404运输巷垂直煤墙平行布置5个大直径煤层钻孔。结合前文研究知晓：孔间距缩短可增强煤层瓦斯预抽效果，满足煤层预抽采达标需求，但会造成瓦斯治理成本剧增。以6个月作预期抽采达标期，可得出对应直径为Φ 300 mm大直径煤层钻孔间距为6.0 m，考虑到瓦斯含量均低于11.21 m³/t，适当增大孔间距至8.0 m。设计参数为：抽采负压2.0 kPa左右，孔径为Φ 300 mm，孔间距为8.0 m，孔深100 m。

图 12 工作面平面图

Figure 12. Schematic diagram of the layout of the working face

下载: 全尺寸图片幻灯片

3.1 试验方案及工艺流程

图13为大直径煤层瓦斯抽采钻孔施工工艺。① 移动钻机定位，开孔位置切开护网。铺设钻机位置距离煤壁开孔处约1.5～3.0 m，考虑到煤厚3.0 m，为保证钻孔抽采覆盖全煤层，开孔高度不低于1.0 m。打钻之前，应将开孔位置处护网切开400 mm×400 mm。② 实施133 mm基本孔。通过移机后在2404运输巷进行基本孔开孔和扩孔操作，钻杆连接直径133 mm钻头，配合导向钻杆开口施工基本孔钻进到预定处。③ 133 mm基本孔扩孔成0.30 m钻孔。钻进到位后，扩孔更换300 mm钻头连接普通钻杆采用旋转钻进方式扩孔100 m。

图 13 大直径瓦斯抽采钻孔施工工艺

Figure 13. Construction process of large-diameter gas extraction drilling

下载: 全尺寸图片幻灯片

3.2 现场监测及分析

自钻孔纳入抽采日起，持续监测抽采180 d内各个钻孔的瓦斯抽采体积分数变化。从施工钻孔中优先选取数据较全面的测试钻孔作考察对象并绘制相关曲线，180 d 300 mm大直径钻孔和普通75 mm单孔瓦斯体积分数变化如图14所示。

图 14 瓦斯体积分数随抽采时间变化

Figure 14. Variation of gas volume fraction with extraction time

下载: 全尺寸图片幻灯片

就0～180 d内单孔瓦斯体积分数抽采情况而言，0.30 m大直径煤层单孔瓦斯体积分数钻孔普遍高于0.075 m本煤层小钻孔。K1号0.30 m大直径钻孔单孔瓦斯体积分数最大值达到了47.2%，而0.075 m单孔瓦斯体积分数最大值仅为10.6%，两者相差36.6%。就服务周期看，两者单孔瓦斯体积分数随时间推进而逐步降低，但大直径钻孔高瓦斯体积分数（5.0%以上）抽采期高达122 d，小钻孔高瓦斯体积分数（5.0%以上）抽采期维持仅107 d，大直径钻孔抽采期延长了40.2%，表明采用大直径煤层钻孔卸压使周围煤岩产生了更大的损伤破坏，使孔周煤体渗透性明显提高。

综上，大直径煤层钻孔对煤层卸压增透显著，实现储层瓦斯资源的高效抽采，是煤与瓦斯共采有效保障技术，补全了矿井瓦斯治理技术体系空白，进一步完善了钻孔瓦斯抽采工艺，对工作面瓦斯防治具有指导意义。

4. 结　　论

1）考虑煤体长时效应破坏的影响，构建了大直径钻孔卸压煤层瓦斯运移多场耦合模型，分析其塑性区和破坏区半径随抽采时间变化规律，发现：抽采时间一定时，随着大直径钻孔孔径的增加，塑性区和破坏区半径随之增大。

2）提出了大直径钻孔瓦斯有效抽采半径的判定指标——残余瓦斯压力不超过0.22 MPa。单一大直径钻孔煤层瓦斯压力呈以钻孔为圆心的椭圆分布，由钻孔向外瓦斯压力逐渐增加，随抽采时间增加，抽采达标区域逐渐扩大。孔周垂直应力转移特征为随抽采时间增加呈先增后降趋势。

3）多孔周边瓦斯压力变化以中心钻孔为中心呈对称分布规律，但受多孔抽采叠加效应作用下，两孔中心地带的瓦斯压力明显低于孔另一侧等距离处的瓦斯压力。当孔间距为4.0、6.0、8.0 m时，300 mm三孔周边瓦斯压力分别呈现出“两小一大”“三个均匀圆”和“两大一小”的分布，确定大直径钻孔间距为6.0 m。

4）现场实践表明，大直径钻孔瓦斯体积分数远超普通钻孔，前者瓦斯体积分数最大值高达47.2%，后者瓦斯体积分数最大值仅为10.6%，且大直径钻孔5.0%以上高体积分数抽采天数提高了40.2%，煤层增透效果优于普通钻孔。

物质对微波的透射、反射和吸收示意

下载: 全尺寸图片幻灯片

微波辅助不同量Fe催化低阶煤热解半焦SEM 图像［8］

下载: 全尺寸图片幻灯片

微波辅助低阶煤催化热解焦油族组分分布［54］

下载: 全尺寸图片幻灯片

微波辅助煤热解提质中试装置［63］

下载: 全尺寸图片幻灯片

微波加热与传统加热对比［9］

下载: 全尺寸图片幻灯片

辐射时间对褐煤微波干燥升温和含水率的影响［24］

下载: 全尺寸图片幻灯片

添加不同吸波剂对印尼褐煤微波脱水特性的影响［28］

下载: 全尺寸图片幻灯片

褐煤微波干燥过程孔隙和裂纹形成［32］

下载: 全尺寸图片幻灯片

热解温度对褐煤微波热解焦油收率的影响［37］

下载: 全尺寸图片幻灯片

金属化合物吸收微波［48］

下载: 全尺寸图片幻灯片

添加吸波剂强化褐煤微波热解升温特性曲线［49］

下载: 全尺寸图片幻灯片

微波辅助低阶煤催化热解气体组分分布［52］

下载: 全尺寸图片幻灯片

期刊类型引用(8)

1.	张宏图, 周甜, 王登科, 李博涛, 罗勇, 潘荣生, 唐家豪, 卢卫永. 基于应力–扩散–渗流耦合模型的低渗煤层水力割缝增透效果分析. 煤田地质与勘探. 2025(06) 百度学术
2.	易恩兵. 不同循环加卸载路径含瓦斯煤体变形—渗流特征. 能源与环保. 2025(02): 1-8 . 百度学术
3.	王勃，徐凤银，刘文革，邵嗣华，王宁，文建东，程国玺，屈争辉，谢亚东，韩甲业，李志，徐波，杨卫华，张艺腾，李长兴. 煤矿瓦斯动力灾害地面治理关键技术与应用. 煤田地质与勘探. 2025(04): 30-45 . 百度学术
4.	刘勇，张汶定，陈长江，魏建平，徐向宇，张宏图，南勤聪，校朋伟. 松软煤层无水化增透理论及技术发展趋势. 煤炭学报. 2025(04): 2123-2146 . 百度学术
5.	袁腾飞，闫才，孔震，韩飞，徐波. 复杂高应力区掘进工作面冲击地压发生机理与防治技术研究. 煤矿现代化. 2024(05): 66-72 . 百度学术
6.	梅安平. 基于节流压降原理的煤层段水力造穴钻头研究. 煤矿安全. 2024(10): 207-213 . 百度学术
7.	兰安畅. 高瓦斯厚煤层穿层钻孔瓦斯抽采方案模拟优化. 当代化工研究. 2024(19): 122-124 . 百度学术
8.	杨鹏，吕伟伟，周梦影，刘洋，吴攀飞，任亚龙. 可控冲击波煤层增透技术在吉宁煤矿的应用. 中国矿业. 2024(S2): 308-313 . 百度学术