0 引 言
研究的露天煤矿可采及局部可采煤层共21层,现开采深度70 m,随着采深的增加,矿坑东帮边坡与外排土场共同构成一个高大的复合边坡。同时该矿岩性较软,存在多处弱层,构成高大软岩复合边坡[1]。随着我国露天煤矿开采深度逐渐向100 m深度发展,普遍存在有软岩复合边坡,边坡变形问题逐渐凸显,因此,研究露天矿软岩复合边坡的变形机理对边坡滑移的预防和控制具有指导意义。关于软岩边坡的研究,王建良等[2]对软岩边坡的力学性质及变形进行了研究;罗敏等[3]论述了软岩的蠕滑特征;吴维[4]对降雨、边坡高度和坡角对软岩边坡的影响进行研究;徐国民[5]对软岩边坡的滑坡模式及防治工程进行分析并互相验证;杨溢[6]以小龙潭布沼坝矿软岩边坡为背景,研究了矿山爆破对蠕滑边坡的影响。关于复合边坡的研究,朱强等[7]对岩、土复合边坡的滑移模式进行了分析。张莲花等[8]对岩-土复合边坡安全性进行研究并确定危险滑移面。周中等[9]得出雨水进入坡体后,复合边坡的位移随时间变化规律。杨宏海以扎泥河露天煤矿端帮与外排土场构成的复合边坡为研究背景,得出滑坡破坏机理[10]; 对于单一边坡变形机理及稳定性国内外做过许多研究,并取得相应成果。而对于软岩、复合边坡的综合性研究较少,其变形机理的研究成果也比较有限。基于此,着重对软岩复合边坡的变形机理、潜在滑移模式等进行深入研究,并提出稳定型边坡蠕滑机理。
1 边坡模拟方案设计
考虑不同排土高度及排土场与东帮距离情况下的边坡变形机理,制定以下4组方案,见表1。边坡结构及模拟监测点布置如图1所示。
表1 方案设计
Table 1 Program design

方案排弃高度/m东帮与排土场距离/m方案一00方案二20120方案三40120方案四4090
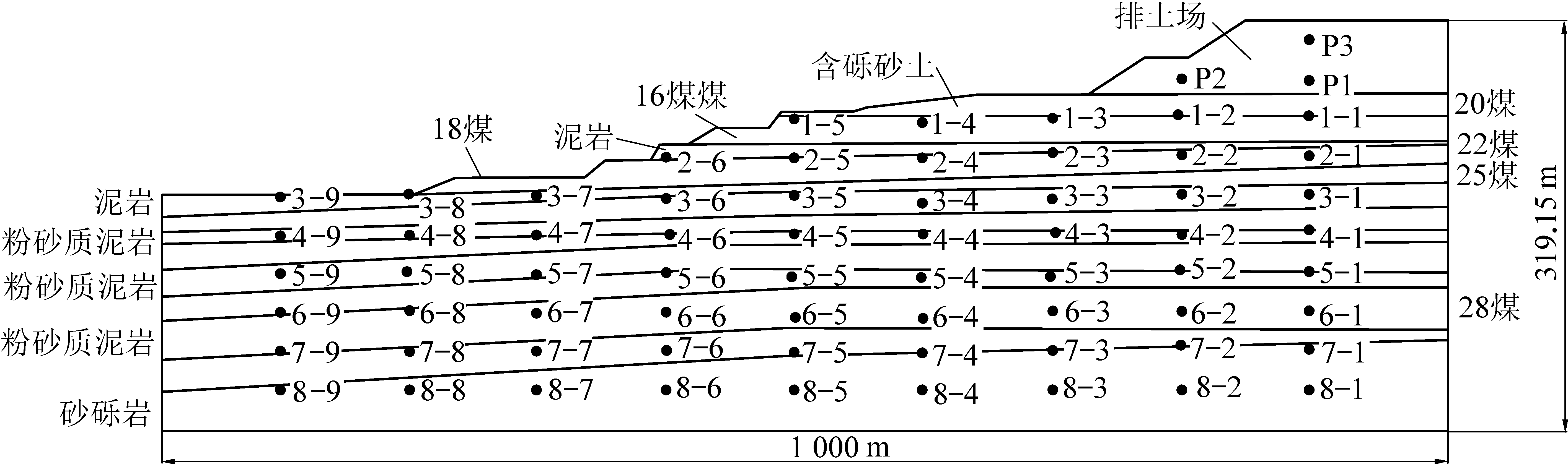
图1 边坡结构及模拟监测点布置
Fig.1 Slope structure and monitoring point arrangement
2 数值模拟分析
2.1 模拟方法及计算参数
边坡数值模拟采用三维快速拉格朗日法,模拟软件选择FLAC3D [11-12]。数值模拟所需的计算参数见表2。
表2 数值模拟计算参数
Table 2 Numerical simulation of calculation parameters
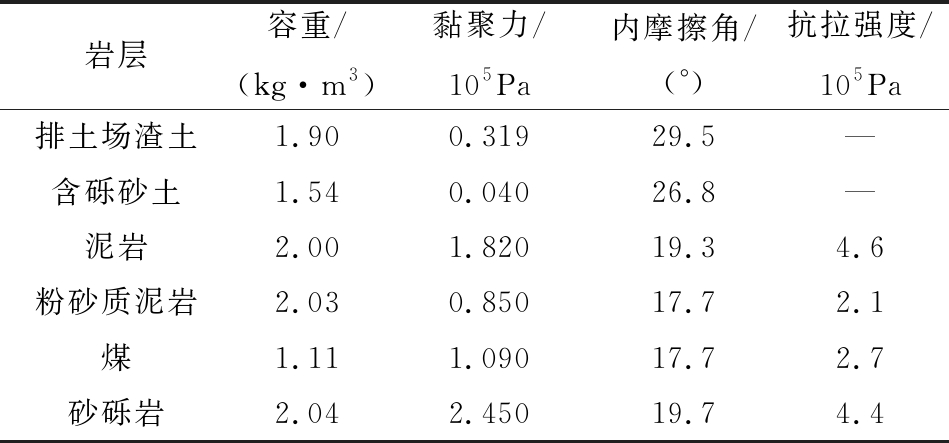
岩层容重/(kg·m3)黏聚力/105Pa内摩擦角/(°)抗拉强度/105Pa排土场渣土1.900.31929.5—含砾砂土1.540.04026.8—泥岩2.001.82019.34.6粉砂质泥岩2.030.85017.72.1煤1.111.09017.72.7砂砾岩2.042.45019.74.4
2.2 模拟结果分析
2.2.1 水平位移分析
各方案水平位移分布图如图2所示。各方案位移云图均以某中心向外扩展,中心处位移最大。在无排土场时,由台阶发展的变形扩展至21煤-22煤处位移达到最大,位移最大处煤层变薄,受挤压明显,沿着煤层弱层发生滑移,说明在无排土场情况下边坡的开挖及弱层对边坡水平滑移影响较大;增加排土场后,最大位移中心发生移动,排弃20 m高时,边坡沿着此处岩层弱面发生切动;排弃至40 m时,最大位移中心移动至排土场坡脚正下方,此位置正是上部排土场张裂隙延展下来与下部弱层的交接点,是组合式滑移的拐点位置,此处受排土场向下的挤压及弱层的双重影响,导致位移较大,同时也说明排土位置对于边坡组合式滑移拐点位置影响较大。
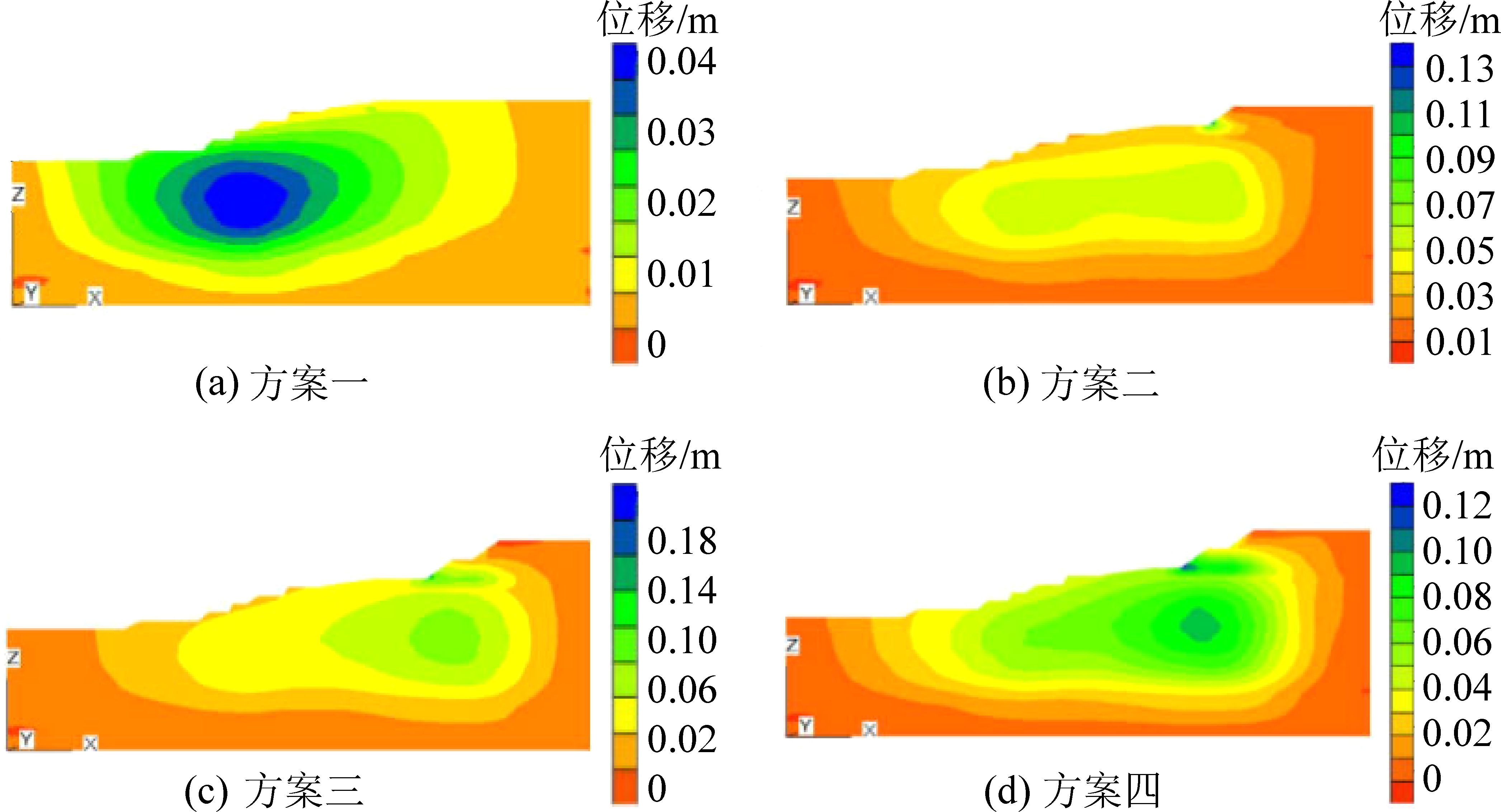
图2 各方案水平位移
Fig.2 Horizontal displacement of different programs
2.2.2 监测点位移随时步变化分析
在模拟过程中对边坡部分监测点位移进行了监测,在此取监测点2-2、2-4、2-6的水平位移随时步变化曲线进行对比分析,如图3所示。
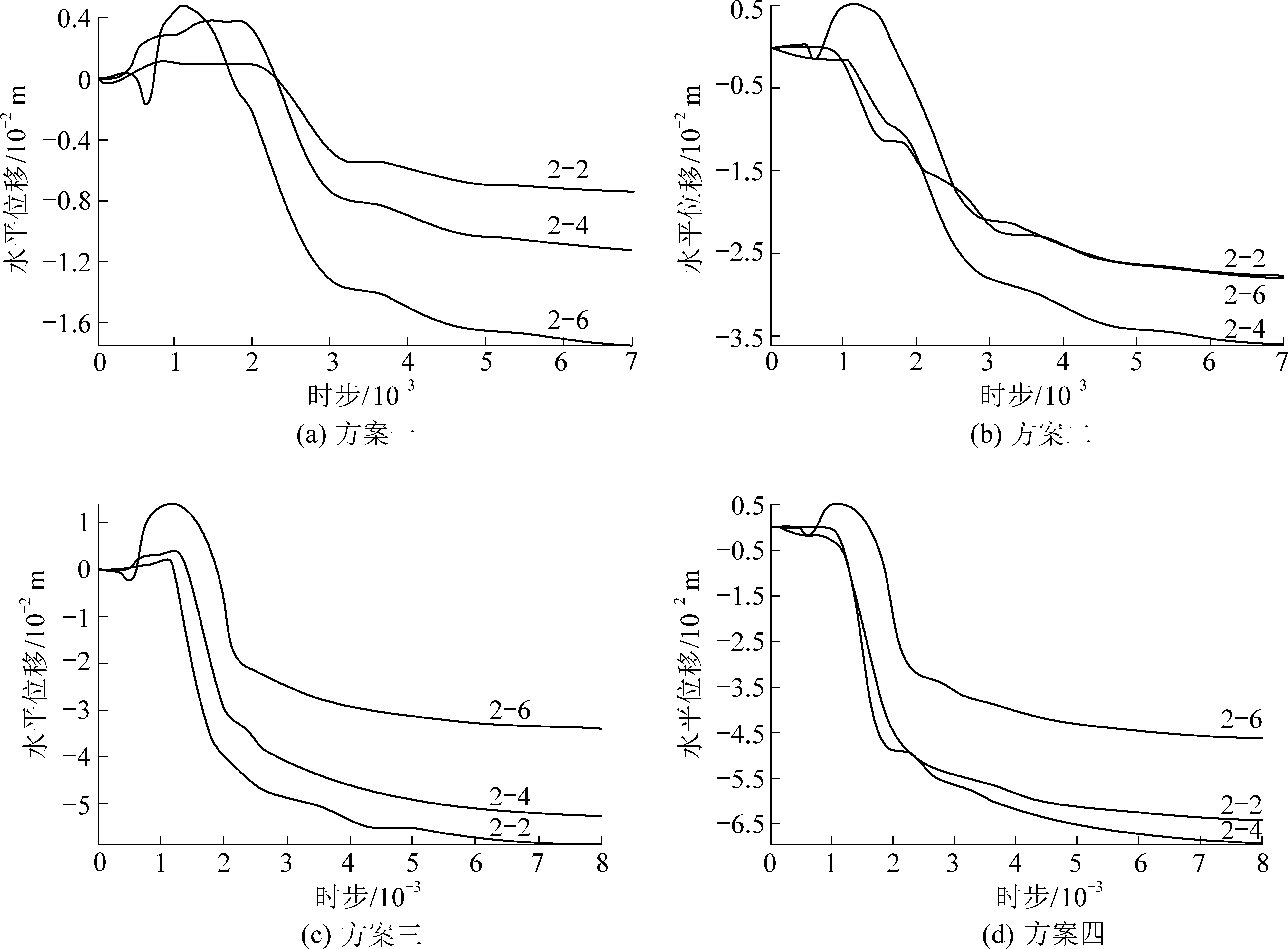
图3 各方案位移随时步变化
Fig.3 Displacement changes with time of different programs
水平位移曲线变化起初均是在0水平上下小幅度变化,之后急速下降,最后下降速度缓慢,并趋于稳定。初期部分曲线向上,出现正向位移,正向位移最大为2-6点,2-6位于台阶下方,受力后最先发生变化。随着排弃高度增加,中期下降速度加快。后期位移趋于稳定,无排土场情况下,位移最大点为2-6,最小为2-2,说明此种情况下水平位移最大发生在受台阶影响的边坡外侧,向内逐渐减小;排弃20 m,水平位移最大是2-4,同距离条件下,排弃高度40 m,最大位移点为2-2,表明排弃越高,受排土场荷载及重心作用,最大水平位移位置向边坡内侧移动;对比方案三和方案四,可得排土场距东帮距离越远,水平位移最大点向边坡内侧移动,说明排土场排弃范围影响水平位移大小。对比各图可得,随着排弃高度增加,水平位移曲线初期波动上升时间减小,中期下降速度加快,后期趋于稳定时间增加。数值模拟监测点的位移均是经历先波动,后增加,再趋稳的3个阶段。综合分析排土场与东帮之间的作用机理,变形过程中由于下部岩体对上部排土场的约束作用减小和排土场对下部岩体的挤压作用产生边坡变形连锁效应,加快边坡变形。
3 边坡变形机理分析
3.1 变形机理综合分析
通过数值模拟对软岩复合边坡在4种工况下的变形时空关系做了分析,对变形机理从复合、软岩、开挖3个方面做进一步总结分析。
3.1.1 复合作用
1)排土场对东帮作用。由排土场坡顶向下发育延伸张拉裂隙,向下贯通与水平弱层连接;由于排土场的荷载作用,挤压下部原本软弱的岩层,使之发生变形,加剧边坡沿下部弱层蠕滑;裂隙分割形成块体,在排土场的倾推作用下,发生偏转,并沿弱层切动,水平位移增大;排土场对东帮的影响从内至外、从上到下逐渐减小;排土场排弃越高、东帮与排土场距离越近,排土场对下部边坡变形影响越大。
2)东帮对排土场作用。东帮台阶坡脚或坡顶受应力集中作用发生变形,由于拉应力大于岩体抗拉强度而产生拉裂隙。裂隙将边坡表层分割成块体,形成不同变形分离体,使得下部及外侧岩体对上部排土场的约束作用减弱,当裂隙发展到一定程度,上部排土场在重力作用下将向下部变形和滑移。因此,东帮与排土场之间产生连锁效应。
3.1.2 软岩作用
一方面,岩层本身软弱,另一方面,煤岩交界面构成的弱面成为易滑区。软岩的影响主要为产生塑性变形、加剧裂隙扩展分割块体、构成蠕滑区域。弱层流变退化导致上部岩层基础被掏空,上部岩体包括排土场拉裂形成张拉裂隙,裂隙延伸至下部弱层时停止;由于东帮邻空,水平应力得到释放并产生卸荷回弹,当上部岩体下滑力超过实际抗滑力,即发生剪裂,向邻空面蠕滑。
3.1.3 开挖作用
由于露天矿的开采,随着矿坑地推进与延伸,形成边坡邻空面。邻空面的应力释放,导致边坡有向坑内滑移趋势,产生向下的形变拉应力,致使上部排土场受下部牵引作用,使之与其一起向下部移动[13-16]。
3.2 边坡潜在滑移模式
通过模拟,综合分析得出4种工况下边坡的滑移模式:无排土场情况下,边坡受东帮台阶应力集中产生拉裂隙与下部弱层相连,弱层发生蠕滑,滑移模式为拉裂-蠕滑,直线型;排弃高度20 m、排土场与东帮距离120 m时,台阶拉裂带扩展与下部弱层相连,弱层发生蠕滑,但蠕滑区较无排土场工况下变大,滑移模式为拉裂-蠕滑,直线型;排弃高度40 m、排土场与东帮距离120 m时,蠕滑中心内移,排土场拉裂隙向下发育,排土场对下部边坡倾推挤压,岩层间产生剪切,发生切层滑动,与下部弱层相连,形成剪切变位,由弱层区域向外产生蠕滑,滑移模式为拉裂-切层-蠕滑,折线型;排弃高度40 m、排土场与东帮距离90 m时,排土场拉裂隙向下发育,由于排土场与东帮距离减小,排土场对下部边坡影响范围增大,因此在排土场倾推作用下产生的切层区变陡,切层区与下部弱层相连,形成剪切变位,加剧弱层蠕滑,蠕滑作用及排土场作用的增强导致滑移带沿坡脚附近剪出,滑移模式为拉裂-切层-蠕滑-剪出,曲线型[17-18]。各工况下滑移模式如图4所示。
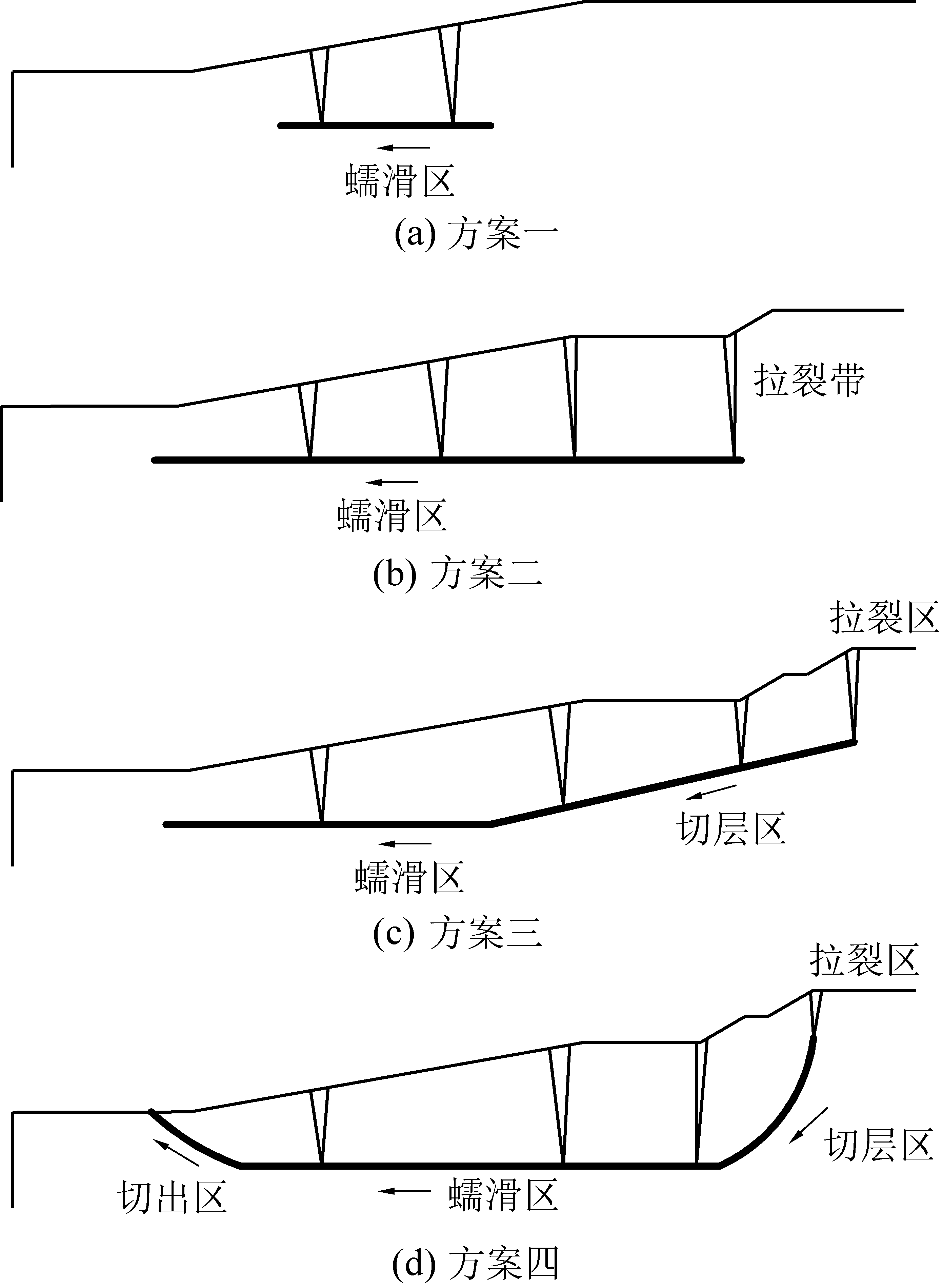
图4 不同方案边坡滑移模式示意
Fig.4 Observation of slope slip mode under various operating conditions
3.3 边坡蠕滑机理研究
3.3.1 失稳型边坡蠕滑机理
对软岩边坡蠕滑的研究,往往建立在边坡失稳的条件下,即边坡最终发生破坏,直至滑坡,变形过程经历5个阶段,如图5a所示。初始变形阶段(O-A):该阶段主要为弹性变形阶段,此时边坡变形并未进入蠕滑阶段,下滑力的作用主要与边坡结构因素有关,与时间无关。减速蠕变阶段(A-B):此时边坡进入蠕滑阶段。由于岩体的压实及结构调整,产生弹性后效变形,蠕变速率随时间的增加而减小,至B点最小。等速蠕变阶段(B-C):坡体应力的调整使得裂隙均匀增加,此阶段应变速率保持不变。加速蠕变阶段(C-E):在等速变形基础上,边坡变形速率不断增加,至E达到峰值,变形剧烈而导致边坡失稳破坏[19-20]。
3.3.2 稳定型边坡蠕滑机理
受外力影响,边坡发生变形,但有的时候边坡并未发生滑坡,而是处于稳定状态。因此,在原有失稳型边坡蠕滑机理基础上,提出稳定型边坡蠕滑机理,对原有蠕滑模型进行改进,得到稳定型边坡变形过程,如图5b所示。初始变形阶段(O-A):该阶段主要为弹性变形阶段,此时边坡变形并未进入蠕滑阶段,下滑力的作用主要与边坡结构因素有关,与时间无关。减速蠕变阶段(A-B):此时边坡进入蠕滑阶段。岩体的压实及结构调整,产生弹性后效,蠕变速率随时间的增加而减小,至B点最小。等速蠕变阶段(B-C):坡体应力的调整使得裂隙均匀增加,此阶段应变速率保持不变。减速蠕变阶段Ⅰ(C-D):边坡变形以C为转折点,由于边坡不具备滑坡破坏条件,塑性变形逐渐减小,变形速率减小。减速蠕变阶段Ⅱ(D-E):经D以后,边坡变形进一步减小,由塑性变形向弹性变形转化,变形速率逐渐减小且趋于零,到E点边坡处于稳定状态。
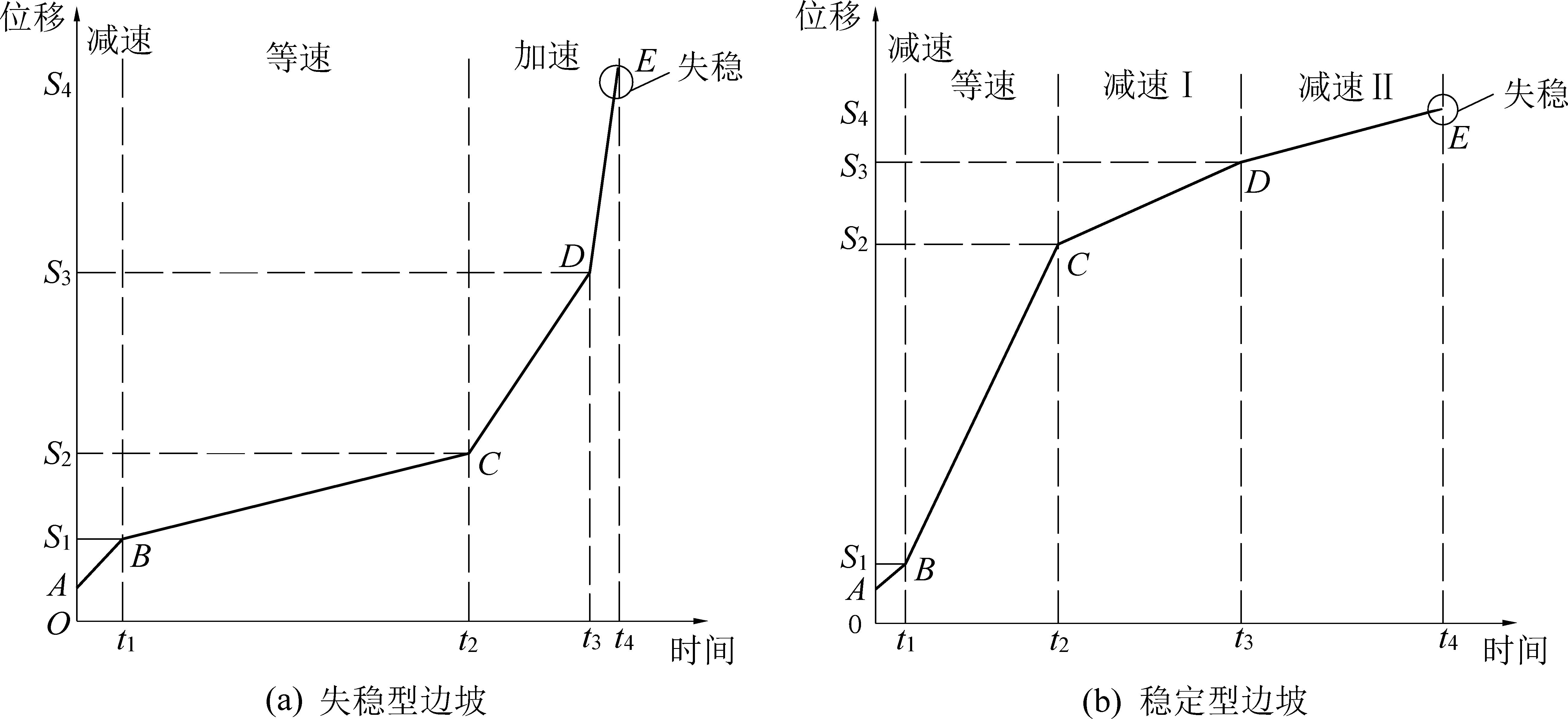
图5 边坡变形阶段示意
Fig.5 Analysis of deformation stage of slope
3.3.3 东帮与外排土场复合边坡蠕滑变形分析
由图4各工况下滑移模式可知,边坡滑移模式均存在蠕滑区,因此对蠕滑区做针对性研究,选取蠕滑区内监测点4-5,对其数值模拟的应力-位移曲线、位移-时步曲线做对比分析,如图6所示。其中位移-时步曲线符合4.3.2提出的稳定型边坡蠕滑机理。初始变形阶段(O-A),边坡应力急速增加,处于弹性变形阶段,此时由于边坡结构因素影响,东帮台阶发生应力集中,并出现裂隙。应力经过回落及小幅调整,边坡进入蠕滑阶段。减速变形阶段(A-B),此时由于上部排土场及其他岩层荷载作用,对下部弱层产生压实作用,变形速率随时间而减小,曲线呈下弯型。等速变形阶段(B-C),裂隙均匀向下扩展,至弱层贯通,上部排土场的倾推作用,使蠕滑区水平位移增大,故此时变形速率较A-B段增加,之后保持稳定速率向坡体外发展。减速变形阶段Ⅰ(C-D),C之后,边坡位移速率较等速变形阶段减小,边坡塑性变形减弱,蠕滑移动速度减慢。减速蠕变阶段Ⅱ(D-E),D之后,边坡位移速率进一步减小,至E点后趋于零,边坡变形趋于稳定,无滑坡风险。
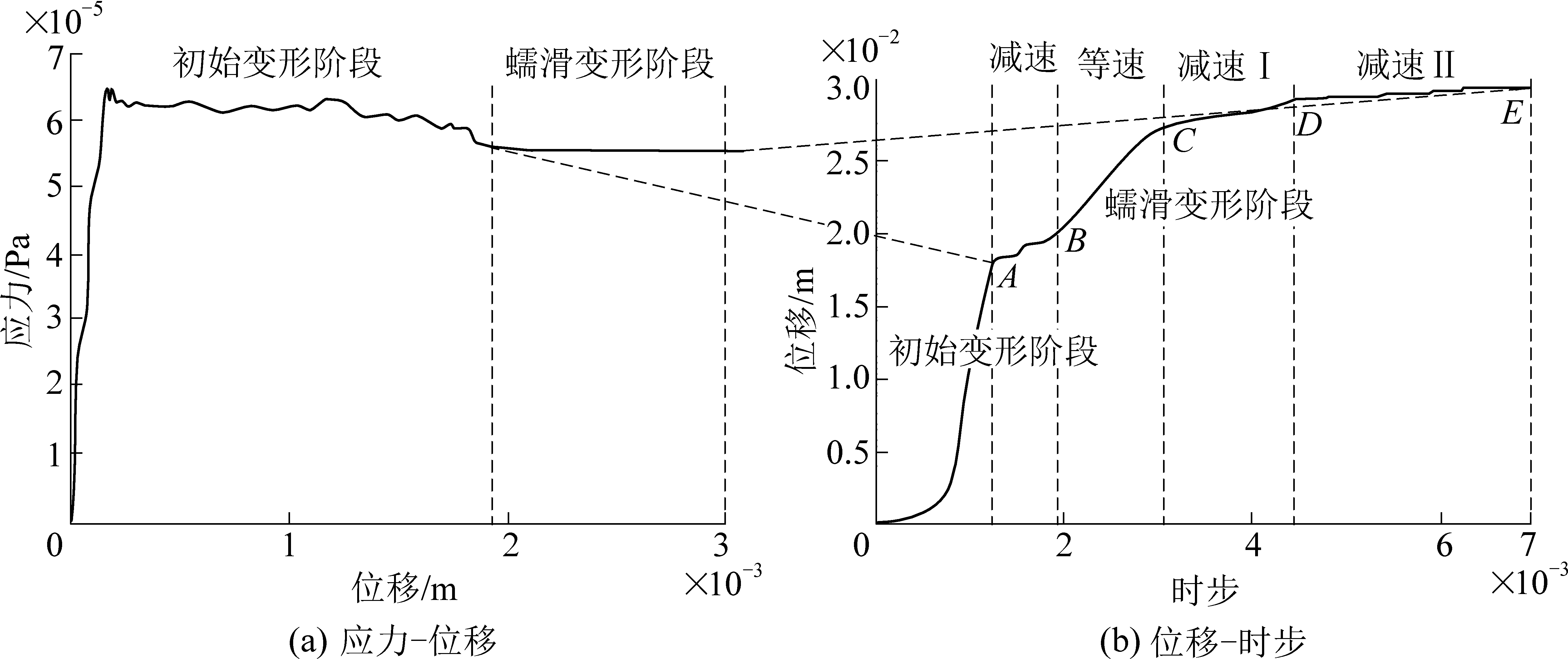
图6 蠕滑区变形过程示例
Fig.6 Example of deformation process of creep zone
4 结 论
1)对软岩复合边坡在不同工况下的变形过程进行了模拟分析,得出监测点位移随时间起初小幅波动,中期下降较快,后期平稳的变化趋势;随着排土场排弃越高,排土场距东帮距离越远,边坡最大水平位移位置向边坡内侧移动。
2)分析不同工况下排土场与东帮之间的作用机理,变形过程中由于下部岩体对上部排土场的约束作用减小和排土场对下部岩体的挤压作用产生边坡变形连锁效应,加快边坡变形;得出软岩复合边坡变形机理主要为复合作用、软岩作用、开挖作用。
3)得出了不同工况下的边坡潜在滑移模式,分别为拉裂-蠕滑,直线型;拉裂-切层-蠕滑,折线形;拉裂-切层-蠕滑-剪出,曲线型。
4)在传统失稳型蠕滑边坡基础上提出稳定型边坡蠕滑机理,主要分为初始变形阶段、减速蠕变阶段、等速蠕变阶段、减速蠕变阶段Ⅰ、减速蠕变阶段Ⅱ,并根据数值模拟结果对其进行验证,对边坡滑移的预防具有一定指导意义。
[1] 孙玉科,姚宝魁,许 兵.矿山边坡稳定性研究的回顾与展望[J].工程地质学报,1998,6(4):52-56.
SUN Yuke,YAO Baokui,XU Bing. Review and prospect of research on stability of mine edges[J]. Journal of Engineering Geology,1998,6(4):52-56.
[2] 王建良,姚 激,蒲秀荣.软岩边坡稳定性的FLAC和刚体极限平衡法对比分析[J].科学技术与工程,2009,8(9):4694-4697
WANG Jianliang,YAO Ji,PU Xiurong.Comparative analysis of flac and rigid body limit equilibrium method for stability of soft rock slopes [J]. Science Technology and Engineering,2009,8(9):4694-4697
[3] 罗 敏.软岩蠕滑的综合整治[J].广东公路交通,1999,61:86-88.
LUO Min. Comprehensive treatment of soft rock creeping [J]. Guangdong Highway Traffic,1999,61:86-88.
[4] 吴 维.考虑降雨入渗影响的软岩边坡过程稳定性研究[D].长沙:长沙理工大学,2013
[5] 徐国民.软岩边坡变形失稳机理及防治技术研究[D].昆明:昆明理工大学,2005.
[6] 杨 溢.爆破荷载对蠕动边坡的累积效应及稳定性影响研究[D].昆明:昆明理工大学,2010.
[7] 朱 强,刘 伟.土—岩混合高边坡锚索(杆)加固前后稳定性分析[J].勘察科学技术,2007(3):13-16.
ZHU Qiang,LIU Wei. Stability Analysis of soil-rock mixed high slope anchor cable(pole) before and after reinforcement [J] .Science and Technology of Investigation and Surveying,2007(3):13-16.
[8] 张莲花,唐凌翔,罗 康.一种土岩混合边坡的稳定性分析计算方法[J].岩土工程技术,2008,22(3):119-122.
ZHANG Lianhua,TANG Lingxiang,LUO Kang.Stability analysis and calculation method of soil-rock mixed slope [J]. Rock and Soil Engineering Technology,2008,22(3):119-122.
[9] 周 中,傅鹤林.土石混合体边坡人工降雨模拟试验研究[J].岩土力学,2007,28(7):1391-1396.
ZHOU Zhong,FU Helin. Simulated experimental research on artificial rainfall on slope of soil-rock mixture [J]. Rock and Soil Mechanics,2007,28(7):1391-1396.
[10] 杨宏海.扎泥河露天矿采场与南排土场复合边坡稳定性分析[D].沈阳:辽宁工程技术大学,2010.
[11] 彭文斌.FLAC 3D实用教程[M].北京:机械工业出版社,2007.
[12] 曹兰柱,赵立春,王 东,等.含多弱层复合边坡滑坡治理三维数值分析[J].中国安全生产科学技术,2015,11(6):102-107.
CAO Lanzhu,ZHAO Lichun,WANG Dong,et al. Three-dimensional numerical analysis of landslide treatment with multiple weak layer complex slopes[J]. China Safety Science and Technology,2015,11(6):102-107.
[13] 卢海峰.巴东组软岩边坡岩体工程特性及破坏机理研究[D].北京:中国科学院,2010.
[14] 任月龙. 露天煤矿软岩复合边坡形成机理及其力学行为特征与开采控制技术[D].徐州:中国矿业大学,2014.
[15] 李良杰,刘旭红,黄生文,等.软岩边坡开挖高度和坡率对边坡稳定性的影响[J].长沙理工大学学报,2012,3(9):36-42.
LI Liangjie,LIU Xuhong,HUANG Shengwen,et al.Influence of excavation height and slope rate of soft rock slope on slope stability[J]. Journal of Changsha University of Science and Technology,2012,3(9):36-42.
[16] 王文忠,冉启发,孙世国,等.露天边坡与山体边坡复合体稳定性分析[M].北京:冶金工业出版社,2001:48-98.
[17] 赵洪宝,李华华,王中伟.边坡潜在滑移面关键单元岩体裂隙演化特征细观试验与滑移机制研究[J].岩石力学与工程学报,2015,5:935-944.
ZHAO Hongbao,LI Huahua,WANG Zhongwei.Study on the meso-experiment and slip mechanism of rock mass fissure evolution in key slip surface of slope[J].Chinese Journal of Rock Mechanics and Engineering,2015(5):935-944.
[18] 王建国,王振伟,王来贵,等.受控于软弱结构面的矿山软岩边坡稳定性[J].辽宁工程技术大学学报,2006,25(5):686-688.
WANG Jianguo,WANG Zhenwei,WANG Laigui,et al.Stability of mine soft rock slope controlled by weak structural plane[J].Journal of Liaoning Technical University,2006,25(5):686-688.
[19] 贺可强,陈为公,张 朋.蠕滑型边坡动态稳定性系数实时监测及其位移预警判据研究[J],岩石力学与工程学报,2016,35(7):1379-1384.
HE Keqiang,CHEN Weigong,ZHANG Peng.Real-time monitoring of dynamic stability coefficient of creeping slope and its displacement early warning criterion[J].Journal of Rock Mechanics and Engineering,2016,35(7):1379-1384.
[20] 苗胜军,蔡美峰,来兴平,等.基于Verhulst模型改进的“斋藤法”变形趋势预报研究[J].中国矿业,2007,16(4):46-50.
MIAO Shengjun,CAI Meifeng,LAI Xingping. Research on the deformation trend prediction of “Saito Method” based on Verhulst model improvement[J].China Mining,2007,16(4):46-50.
