0 引 言
地下采矿工程中的巷道、开切眼、各种开采硐室空间及地下天然洞穴、人工钻孔等,在地下无限大的空间范围内,其围岩破坏及稳定性问题均可统一到孔洞周围岩体力学的研究中[1-2]。孔洞围岩弹塑性力学通过数学和力学的方法,建立起应力与围岩的相互作用机制,使实际条件下复杂的无法解答的工程问题得到科学的量化分析[3]。地下工程压力理论及围岩稳定性分析的发展已有上百年的历史,理论研究主要经历了古典压力理论、散体理论、弹塑性理论等3个发展阶段[4]。20世纪20年代以前主要是古典压力理论阶段,主要代表理论有海姆(Heim A.)、郎金(Rankine W.J.M.)和金尼克(Динник A.H.)理论。从20世纪50年代后期开始,有学者引用弹塑性理论来研究围岩稳定问题,将地下工程围岩稳定分析带入科学理论及定量计算的时代。在此期间,相继出现了著名的芬纳(Fenner R.)公式和卡斯特奈(Kastner H.)公式,推导出了圆孔周围弹塑性应力解及围岩塑性区半径的解析解,奠定了地下工程弹塑性分析的理论基础[5]。
然而,孔洞围岩塑性区边界的理论计算继芬纳公式、卡斯特奈公式之后就再难得到突破。两个公式很好解决了静水压力条件下孔洞围岩的塑性区边界问题,对于非均匀应力场中孔洞围岩塑性区边界的严格计算公式至今仍然没有实现。国内外学者对于非均匀应力场中孔洞周围的弹塑性解做了很多努力,1983年于学馥等[6]著《地下工程围岩稳定分析》中曾给出非轴对称应力条件下圆形隧道围岩塑性区边界线的近似计算方法;2007年陈立伟等[7]基于统一强度理论推导出非均匀应力场中巷道围岩塑性区边界线方程式;2014年赵志强[8]推导出非均匀应力场中圆形巷道围岩塑性区边界八次方隐性方程,并基于八次方隐性方程研究了保德矿非均匀大变形机理,提出了蝶形塑性区的概念。但是以上这些非均匀应力场中孔洞围岩塑性区边界方程在公式推导过程中均作了简化处理,得到的结果为近似解,并非严格意义上的理论结果。
地下实际应力场并非静水压力,尤其煤矿井下受到采动影响及地质构造影响后,围岩将处在非均匀应力场中,处在其中的巷道、硐室通常会变形破坏严重、维护困难,这类巷道、硐室围岩稳定性分析与控制一直都是研究的难点[9-10]。目前关于非均匀应力场中孔洞围岩塑性区边界问题的求解和研究仍然没有更好的办法,一是借鉴芬纳公式作为近似解来分析认识,二是采用边界方程的近似解来解答。芬纳公式推导过程严密但是力学模型为静水压力条件;塑性区边界方程建立了非均匀应力场中应力与围岩的相互作用机制,但是公式推导过程做了简化处理,得到的结果为近似解;2个理论计算公式在解决非均匀应力场中孔洞围岩塑性区边界问题均存在不完美之处。
为了解决非均匀应场中孔洞围岩塑性区边界的问题,必须厘清以下4个问题:2种近似算法可靠性如何,计算的塑性区边界误差如何,能否满足现场工程的精度要求,理论公式在什么条件下能够适用。从理论公式的力学模型入手,具体分析了公式的推导原理、推导过程、计算精度,并结合FLAC3D数值模拟对比研究,分析评价理论公式的适用条件。研究结果对孔洞围岩塑性区边界计算理论的发展及合理利用理论指导现场工程实践有重要意义。
1 静水压力条件下的芬纳公式及卡斯特奈公式
1.1 推导原理和过程
芬纳(Fenner R.)公式假设围岩为均质、各项同性材料,在孔洞长度方向围岩性质一致;将地下应力场简化为轴对称分布的静水压力条件;采用研究平面应变问题的方法,取无限长圆孔的任一截面作为代表进行分析,理论模型如图1所示。静水压力条件下的受力模型由于其对称性,得到的塑性区为均匀分布在圆孔周围的圆环,基于理论模型经过受力分析、公式推导,后又经过修正,最终得到了塑性区边界半径的解析式,即芬纳公式。卡斯特奈公式在芬纳公式的基础上将塑性区边界半径表示为关于岩石抗压强度的表达式,为公式应用带来方便。为了充分认识芬纳公式与卡斯特奈公式,下面详细阐述了2个公式的推导原理和推导过程,为客观分析评价2个公式的理论价值及适用条件奠定基础。
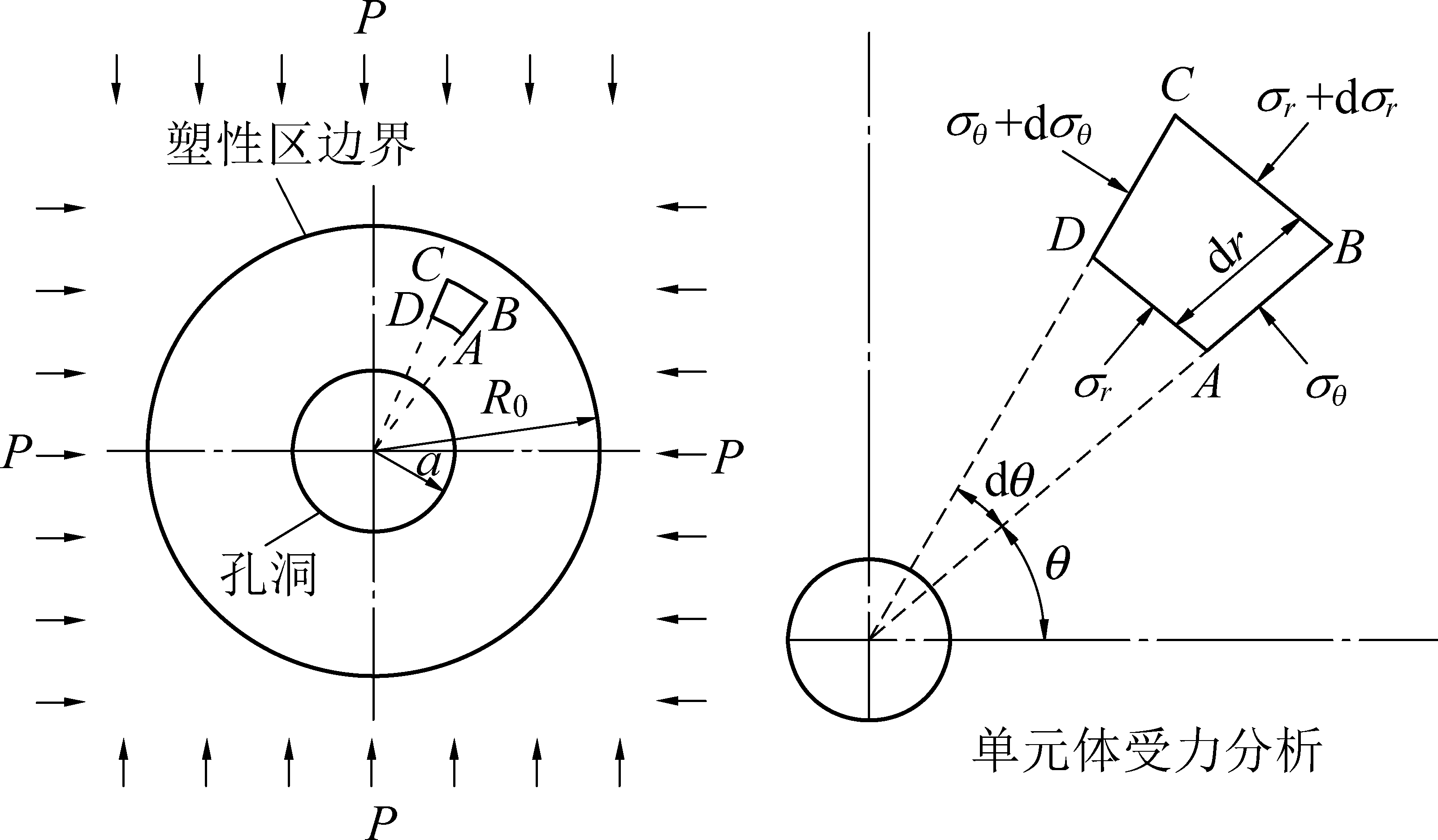
图1 静水压力下孔洞围岩力学模型
Fig.1 Mechanical model of hole surrounding rock under hydrostatic pressure
假设孔洞半径为a,公式在推导中假设塑性区内岩石黏聚力C和内摩擦角φ是常数,相比地应力的量级,模型范围内的岩体重力可以忽略,根据单元体受力分析得平衡微分方程为
(1)
其中:r、θ为微单元的极坐标,m、rad;σr、σθ为分别径向应力与切向应力,MPa。忽略公式(1)中的高次微分项,平衡方程变形为
(2)
塑性区内岩体处于极限平衡状态,基于摩尔-库伦强度准则,得极限平衡方程为
(σr+Ccot φ)(1+sin φ)-(σθ+Ccot φ)(1-sin φ)=0
(3)
令塑性区半径为R0,在巷道周围弹性区与塑性区交界处满足应力协调关系:
(4)
式中:![]() 分别为弹性条件下的径向应力与切向应力,MPa;P为围压,MPa。
分别为弹性条件下的径向应力与切向应力,MPa;P为围压,MPa。
由平衡微分方程式(2)、极限平衡方程式(3)、变形协调关系式(4)求解微分方程,得到圆孔周围塑性区半径R0解析解为
(5)
式(5)就是修正的芬纳公式求得的圆孔围岩塑性区半径解析式。芬纳在推演过程中曾一度假设C=0,因此所得结果与修正公式稍有差异,其式为
(6)
鉴于整个推导的学术思想为芬纳所提,故修正的芬纳公式及芬纳公式统称芬纳公式。
若令
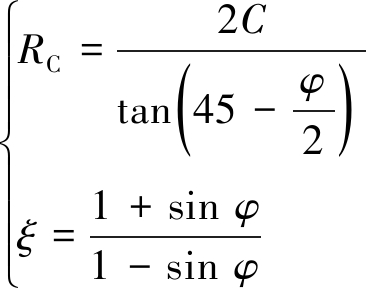
(7)
式中:RC为围岩的单轴抗压强度,MPa。芬纳公式即
(8)
公式(8)即静水压力条件下卡斯特奈(Kastner H.)公式计算的圆形巷道围岩塑性区边界半径解析式。
1.2 评价认识
通过对2个公式的力学模型、推导原理、推导过程的分析可知,力学模型将地下空间围岩结构简化为圆形孔洞的平面应变受力模型,将地下围岩所处应力场设为静水压力,理论公式的推导原理及推导过程完全符合力学原理,2个公式均经过严格的弹塑性理论推导所得,理论公式具有较高的可靠性。理论公式自建立经过了长期实践的检验,在地下工程实践中发挥了重要作用,也是目前应用比较广泛的理论公式。芬纳公式与卡斯特奈公式的力学模型为静水压力条件,对于受采动影响及地质构造影响的非均匀应力场环境是否仍然适用,将在下文适用性分析小节中详细阐述。
2 非均匀应力场中圆孔周围弹性应力解
2.1 推导原理和过程
非均匀应力场中圆孔围岩的弹塑性解较均匀应力场条件下求解难度加大,却是实际工程的切实需要。非均匀应力场中圆孔周围弹性应力解析解对于认识巷道周围应力场分布规律及分析巷道围岩破坏机理有重要作用,目前已有的非均匀应力场中圆孔围岩塑性区边界方程的求解也完全依靠弹性应力解。非均匀应力场中圆孔周围弹性应理解的求解同样假设围岩为均质、各项同性材料,在巷道长度方向围岩性质一致,只是将轴对称静水压力加载条件设置为双向非等压应力加载条件,力学模型如图2所示,其中,λ为侧压系数,当λ=1时为静水压力条件,双向非等压加载条件具有更广泛的适用意义。
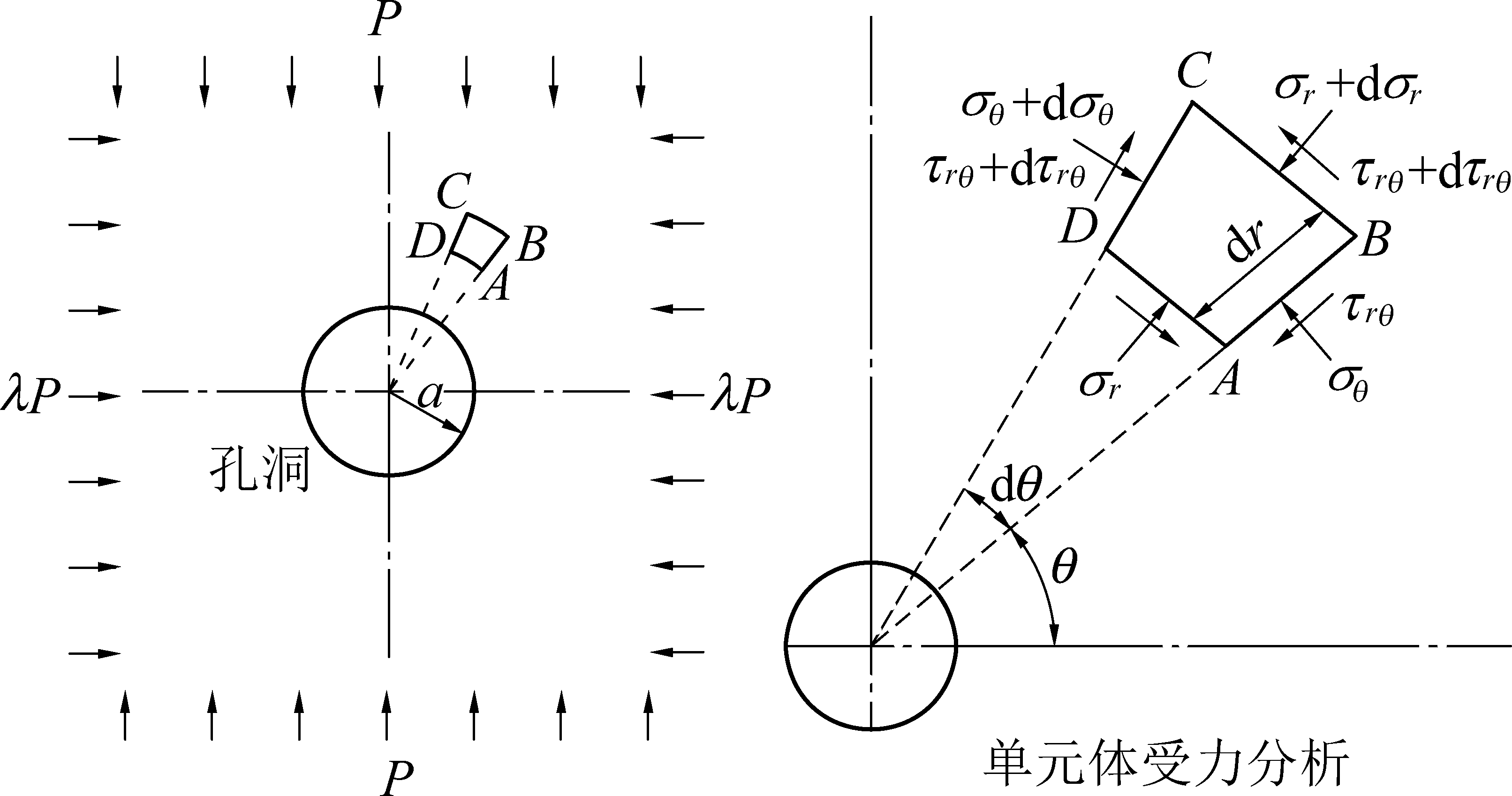
τrθ—剪应力,MPa
图2 非均匀应力场中孔洞围岩受力模型
Fig.2 Stress model of hole surrounding rock in non-uniform stress field
由图2单元体受力分析得平衡方程:
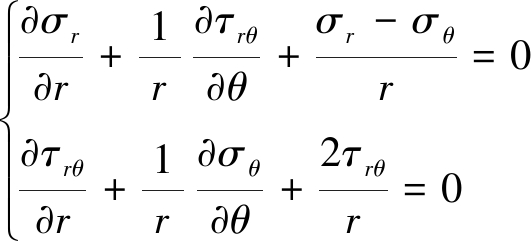
(9)
满足几何方程:
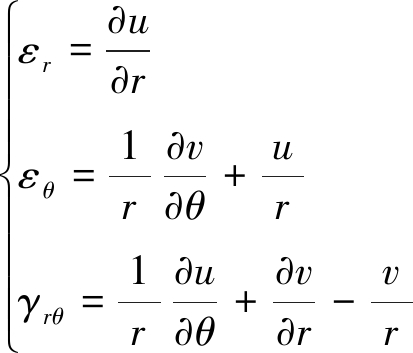
(10)
式中:u、v分别为径向和切向位移,m;εr、εθ、γrθ为极坐标下的应变分量,分别为径向应变、切向应变和剪切应变。
满足物理方程:
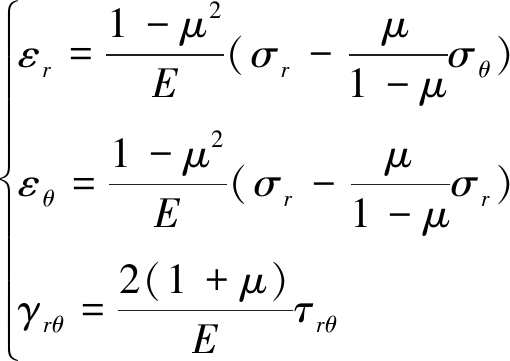
(11)
式中:E为弹性模量,GPa;μ为泊松比。
满足变形协调方程:
(12)
由边界条件r=a,有
σr=0,τrθ=0
(13)
及r=∞时有
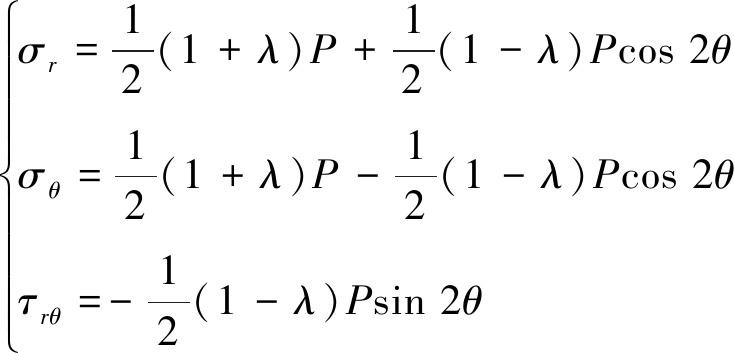
(14)
结合平衡微分方程、几何方程、物理方程、变形协调方程及边界条件得非均匀应力场中圆孔周围弹性应力解析解:
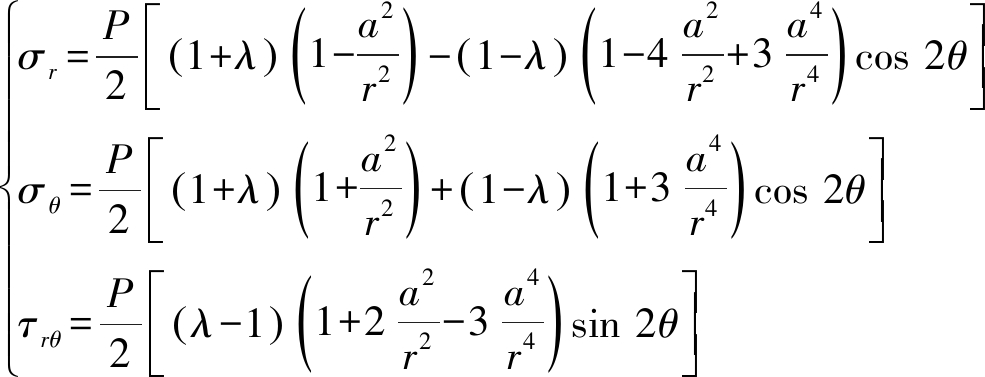
(15)
公式(15)即为非均匀应力场中圆孔周围弹性应力解析解。
2.2 评价认识
固体材料在受力发生破坏前首先经历弹性变形阶段,非均匀应力场中圆孔周围弹性应力解析解为地下井巷工程围岩稳定性分析提供了理论基础,对于认识地下空间周围应力场分布规律及分析围岩破坏规律有重要作用。通过对非均匀应场中圆孔周围弹性应力解析解的力学模型、推导原理、推导过程的分析可知,其力学模型与静水压力下的模型相似仍然将地下空间围岩结构简化为圆形孔洞的平面应变受力模型,只是将静水压力条件变为由侧压系数表示的双向非等压条件;孔洞围岩弹性应力解析解通过平衡微分方程、几何方程、物理方程及变形协调方程严格推导求得的理论结果,其推导原理及推导过程完全符合弹性力学原理,理论公式具有较高的可靠性。
3 非均匀应力场中圆孔围岩塑性区边界方程
3.1 卡斯特奈近似解
卡斯特奈(Kastener H.)曾经提出非均匀应力场中塑性区边界线的近似算法,得到了塑性区边界线的近似解方程,即非均匀应力场中的卡斯特奈近似解[4]。卡斯特奈公式的近似算法是将非均匀应力场中圆孔周围弹性应力解代入到岩石的强度准则中(M-C强度准则):
(16)
将公式(15)代入公式(16)得到非均匀应力场中圆孔围岩塑性区边界卡斯特奈近似解:
![]()

![]()
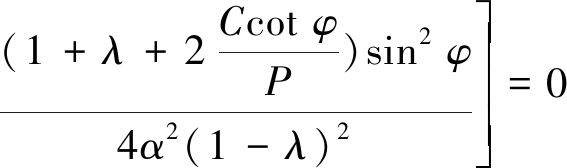
(17)
式中:ω=α2sin2 φ+2-3α2;α=a/R0。
在非等压条件下,当围岩条件及加载条件给定时,圆孔围岩塑性区边界R0已不再是常数,而是满足公式(17)的隐性方程。公式(17)计算的塑性区边界没有考虑塑性应力的重分布,实际上材料达到强度极限后应力会重新分布,所得到的塑性区也会发生变化,所以公式(17)为非等压条件下圆孔围岩塑性区的近似解。
3.2 于学馥圆形隧道围岩塑性区边界的近似计算
公式(17)没有考虑塑性应力的重新分布,所计算的塑性区边界为近似结果。实际上由于塑性应力的重新分布,应力会不断调整,围岩塑性区会不断扩大。1983年于学馥等提出了考虑塑性应力重新分布的圆形隧道围岩塑性区边界线的计算方法[6]。该方法通过2次近似计算获得塑性区边界方程,即先由卡斯特奈方法初次计算得到塑性区半径,然后按塑性区应力方程求解得到所求点的应力![]() 和
和![]() 按所求点的半径作圆,在
按所求点的半径作圆,在![]() 和
和![]() 的作用下,再按照卡斯特奈方法导出新的塑性区边界线方程。
的作用下,再按照卡斯特奈方法导出新的塑性区边界线方程。
为推导出圆孔围岩硐壁上作用有径向力和剪应力的塑性区边界线方程,先要求出以Pi和τi为硐壁作用力的周围弹性应力场公式:
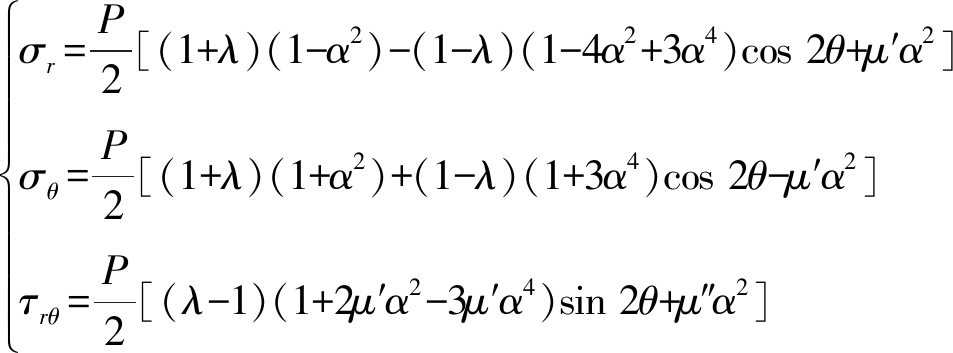
(18)
其中:μ′=2Pi/P,μ″=2τi/P;Pi和τi分别为作用在洞壁上的径向力和剪应力。将式(18)代入岩石的强度准则(16)中,得到围岩硐壁上作用有Pi和τi的塑性区边界线方程
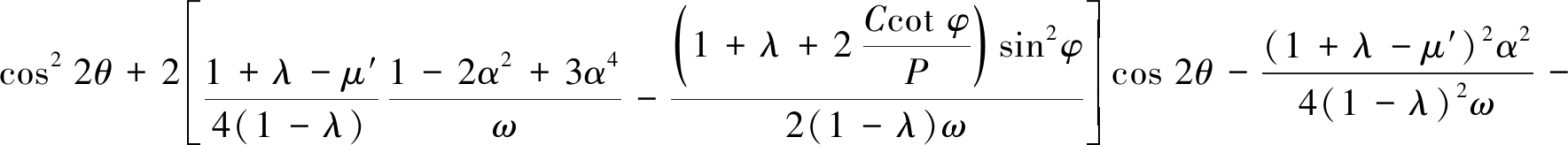
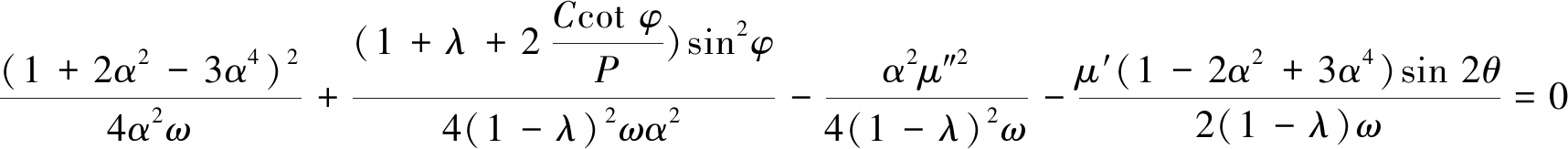
(19)
公式(19)是先由卡斯特奈方法初次计算得到塑性区半径,然后按照塑性区应力方程求解得到所求得的应力值![]() 和
和![]() 按照所求点的半径作圆,在
按照所求点的半径作圆,在![]() 和
和![]() 的作用下,再按照卡斯特奈方法导出新的塑性区边界线方程。该求解方法在求解某种条件下孔洞围岩某一位置的塑性区半径时,需要首先根据卡斯特奈公式求出该位置的第1次近似解,然后确定作用在该处的硐壁作用力Pi和τi,然后代入(19)方程求解。方程(19)经过2次近似计算,计算塑性区半径较卡斯特奈近似解更准确,然而计算过程相对复杂,求解某一点处塑性区半径可行,研究某种条件下塑性区边界线分布情况几乎无法做到。
的作用下,再按照卡斯特奈方法导出新的塑性区边界线方程。该求解方法在求解某种条件下孔洞围岩某一位置的塑性区半径时,需要首先根据卡斯特奈公式求出该位置的第1次近似解,然后确定作用在该处的硐壁作用力Pi和τi,然后代入(19)方程求解。方程(19)经过2次近似计算,计算塑性区半径较卡斯特奈近似解更准确,然而计算过程相对复杂,求解某一点处塑性区半径可行,研究某种条件下塑性区边界线分布情况几乎无法做到。
3.3 基于统一强度理论的圆形巷道围岩塑性区边界线方程式
采用摩尔-库伦强度准则忽略了中间主应力,为了反映中间主应力对材料破坏的影响,俞茂宏教授于1990年提出了统一强度理论[11]。2007年陈立伟等基于统一强度理论,结合非均匀应力场中圆孔周围的应力解,得到了非均匀应力场中圆形巷道围岩塑性区边界线方程式[7]。如果以材料的黏聚力和内摩擦角作为基本试验参数,且当中间主应力满足σ2≤[(σ1+σ3)+(σ1-σ3)sin φ]/2时,统一强度理论表达式如下
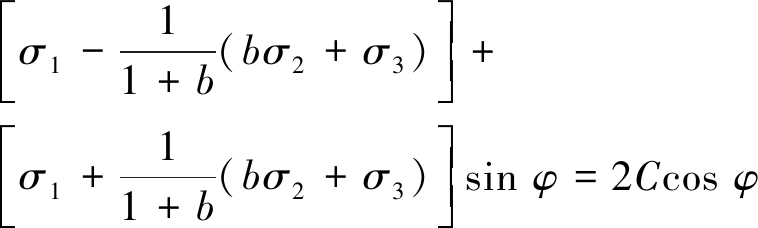
(20)
其中:b为统一强度理论参数,0≤b≤1,反映中间主应力对材料破坏的影响,由材料试验确定。当b=0时,表达式(20)为摩尔-库伦强度准则;当b=1时表达式(20)为广义双剪屈服准则;当0<b<1时,随着b值的不同式(20)可表示为其他强度准则。
基于统一强度理论,陈立伟等将弹性理论求得的圆孔周围应力解代入到统一强度理论的塑性条件来判断围岩的屈服状态。在公式推导中,令σ2≤m(σ1+σ3)/2,m为中间主应力参数,在平面应变情况下,材料达到塑性状态时m向1趋近,中间主应力满足公式(20)的条件。将非均匀应力场中圆孔周围弹性应力解(15)代入统一强度理论(20)中,令k=a2/r2,得到基于统一强度理论的圆形巷道围岩塑性区边界方程式。
f(k)=a1k4+a2k3+a3k2+a4k+a5=0
(21)
式中:a1=9(1-λ)2;
a2=-6(1-λ)[2(1-λ)-(1+λ)cos 2θ];
a5=(1-λ)2-sin2 φt(1+λ+2ctcot φt/P)2;
sin φt=[2(1+b)sin φ]/[b(1+sin φ)+2];
ct=[2(1+b)Ccos φ]/[b(1+sin φ)+2]。
陈立伟等[7]基于统一强度理论求出了非均匀应力场中圆形巷道围岩塑性区边界线方程式,并在文中的算例分析中研究了不同侧压系数下圆形巷道围岩塑性区的边界线分布情况。
3.4 非均匀应力场中圆形巷道围岩塑性区边界八次方隐性方程
为分析井下回采巷道的非对称大变形机理,2014年赵志强推导出非均匀应力场中圆形巷道围岩塑性区边界八次方隐性方程[8],并基于塑性区边界八次方隐性方程的理论研究首次提出了“蝶形塑性区”概念,揭示了大变形回采巷道围岩变形破坏机理。非均匀应力场中孔洞围岩受力模型(图2)中,巷道围岩垂向载荷为上覆岩层自重γH(H为埋深,m;γ为容重,kN/m3),利用侧压系数λ确定巷道围岩水平载荷λγH。根据弹性力学理论极坐标下巷道围岩任一点的应力计算公式(15),基于摩尔-库伦强度准则,将非等压条件下圆形巷道周围任一点的应力计算公式代入强度准则中,经过求解得到非均匀应力场中圆形巷道围岩塑性区边界八次方隐性方程,如公式(22)所示。
(22)
式中:K1=9(1-λ)2
K2=-12(1-λ)2-6(1-λ2)cos 2θ
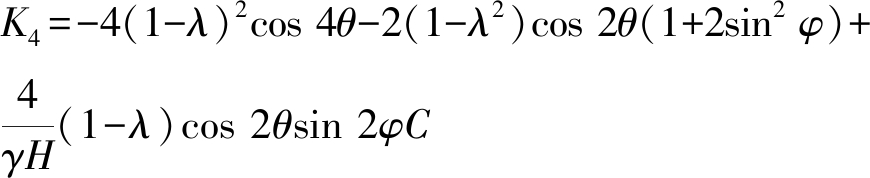
从隐性方程推导原理及推导过程来看,八次方隐性方程仍然是将非均匀应力场中圆孔周围弹性应力解直接代入岩石破坏准则所得,没有考虑塑性应力的变形协调,其结果仍是非均匀应力场中圆孔围岩塑性区边界的近似解。尽管如此,基于非均匀应力场中圆形巷道围岩塑性区边界八次方隐性方程,赵志强在理论上研究了圆形巷道围岩塑性区形态的演化规律,首次提出了“蝶形塑性区”概念,将边界方程的理论研究结果应用于井下实际工程,并通过研究塑性区形态的变化规律揭示了大变形回采巷道围岩变形破坏机理。非均匀应力场中圆孔围岩塑性区边界近似解经长期忽视后再次引起重视,其理论价值再一次被挖掘。
3.5 评价认识
根据前文对非均匀应力场中圆孔围岩塑性区边界方程推导原理和推导过程的阐述,于学馥圆形隧道围岩塑性区边界线的近似计算、基于统一强度理论的圆形巷道围岩塑性区边界线方程式、非均匀应力场中圆形巷道围岩塑性区边界八次方隐性方程,均依据了卡斯特奈近似解的求解思想,即将非均匀应力场中圆孔周围弹性应力解直接代入岩石破坏准则中,均未考虑圆孔围岩塑性应力的变形协调,所得结果均是非均匀应力场中圆孔围岩塑性区边界的近似解。于学馥圆形隧道围岩塑性区边界线的近似解需要经过2次近似迭代,在求解某种条件下孔洞围岩某一位置的塑性区半径时,需要首先根据卡斯特奈公式求出该位置的第1次近似解,然后确定作用在该处的硐壁作用力Pi和τi,然后代入方程(19)求解,计算塑性区半径较卡斯特奈近似解更准确,然而计算过程相对复杂,求解某一点处塑性区半径可行,研究某种条件下塑性区边界线分布情况几乎无法做到。基于统一强度理论的圆形巷道围岩塑性区边界线方程式,其求解原理与卡斯特奈近似解完全相同,只是应用了不同的岩石破坏准则,同时统一强度理论参数b值的获取较困难。非均匀应力场中圆形巷道围岩塑性区边界八次方隐性方程与卡斯特奈近似解实质完全一致,只是表现形式有所不同。到目前为止,关于非均匀应力场中巷道围岩弹塑性的理论计算,卡斯特奈的近似解几乎是目前可以采用的相对较好的方法。
4 分析评价
静水压力条件下圆孔围岩塑性区半径解析解在地下井巷工程稳定性分析及支护设计中被广泛应用,目前被学术界普遍认可;非均匀应力场中塑性区边界方程由于在推导过程中做了简化处理,所得结果只是近似结果,随着后期数值计算的出现边界方程渐渐被学术界所忽视。虽然静水压力条件下圆孔围岩塑性区半径解析解推导过程严密但是力学模型为静水压力条件;塑性区边界方程建立了非均匀应力场中应力与围岩的相互作用机制,但是公式推导过程做了简化处理,得到的结果为近似解;两个理论计算公式在解决非均匀应力场中孔洞围岩塑性区边界问题均存在不完美之处。实际上,即使经过严格推导的理论公式,在解决实际复杂的工程地质问题中都是近似解,但是根据地下工程的特点其准确程度已满足工程需要,这种理论近似结果对于认识指导地下工程实践十分必要。鉴于此,采用理论公式与数值模拟结果对比的方法,详细分析了静水压力下的理论公式与非均匀应力场中塑性区边界方程,具体分析理论计算的可靠性,进而对两个公式的适用性进行评价分析。
4.1 静水压力条件下理论计算的可靠性分析
静水压力条件下孔洞围岩塑性区半径计算公式经过弹塑性理论严格推导所得,在指导静水压力条件下的工程实践方面其可靠性已得到学术界的普遍认可。下文将对理论计算的塑性区半径与数值计算结果进行对比分析,通过研究塑性区的扩展规律,对静水压力下得到的理论公式指导实际地下非均匀应力场中的工程问题的可靠性做进一步分析研究。数值计算采用FLAC3D软件,基于理论公式采用平面应变模型,数值模拟采用方形薄板受力模型,圆孔半径设为2 m,模型边长为120 m,岩石参数选取参考了煤的岩石力学参数[12],取黏聚力C=3 MPa、内摩擦角φ=25°(单轴抗压强度RC=10 MPa),边界应力从10 MPa加载到100 MPa,所得理论计算结果与数值模拟结果如图3所示,其中,红、绿色均为塑性区。
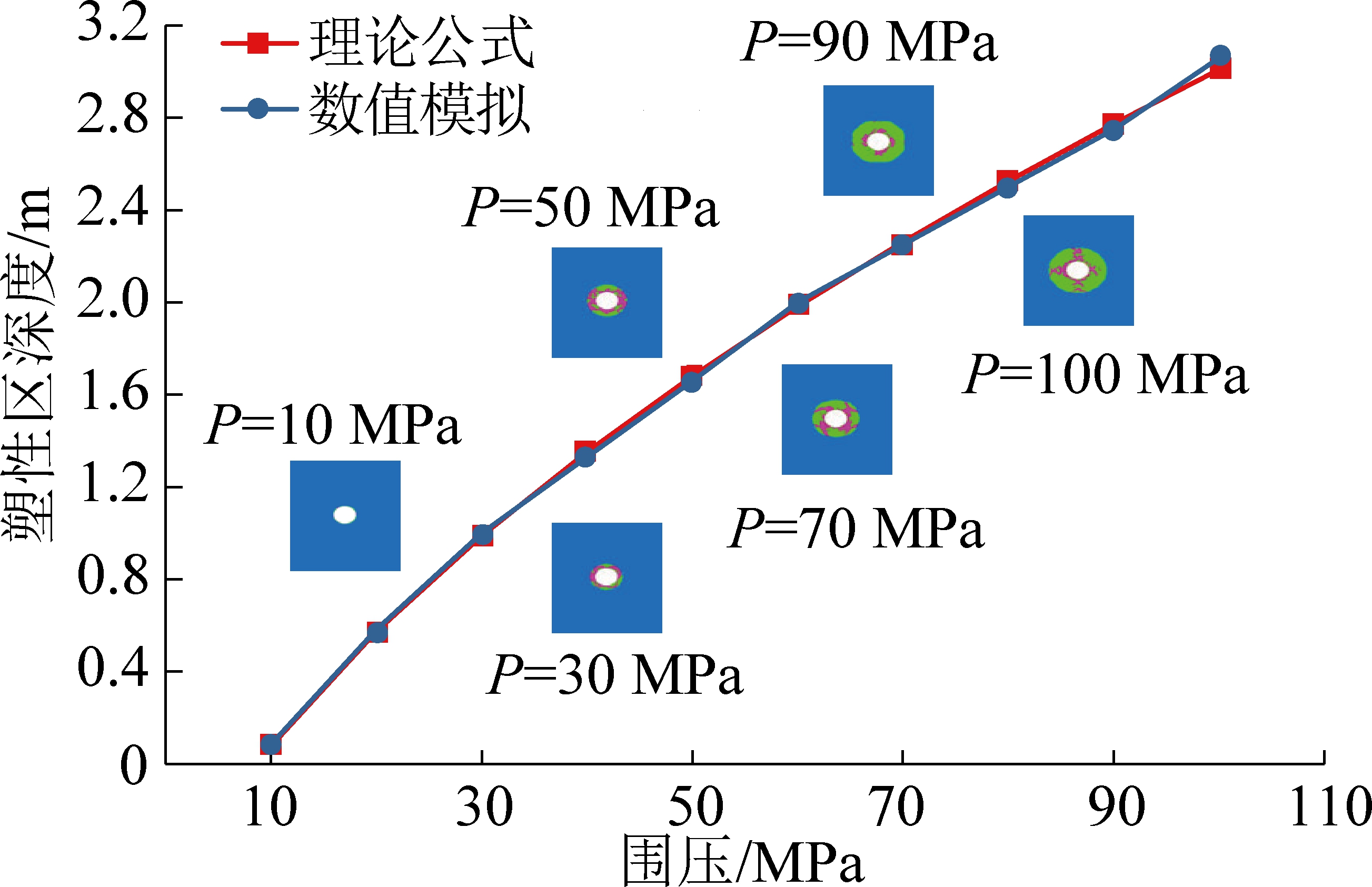
图3 静水压力下圆孔围岩塑性区理论计算与数值模拟对比结果
Fig.3 Comparisons between theoretical calculation and numerical simulation of plastic zone of hole surrounding rock under hydrostatic pressure
由图3可得,理论公式计算结果与数值模拟计算结果几乎重合,证明静水压力下圆孔围岩塑性区半径计算公式具有很高的准确性,这与芬纳公式严密的推导过程是分不开的,基于芬纳公式来指导静水压力条件下地下工程是可靠的。另一方面,由于芬纳公式采用静水压力受力模型,模型关于坐标轴对称,不管施加应力大小如何,得到的塑性区形态均为圆环形状。然而在实际地下条件中,空间围岩很少处在静水压力条件。模型边界应力从10 MPa加载到100 MPa,100 MPa基本相当于埋深4 000 m的应力水平,在我国现有的开采深度条件下几乎不可能达到这么大应力,即使应力加载到100 MPa时,塑性区深度仍然不到3 m,且算例采用的岩石力学参数和强度较弱的煤岩的力学参数相当。在现有的工程条件下,不足千米的煤矿井下,有的大变形巷道围岩变形量甚至可达到1 000 mm以上[13]。如保德矿回采巷道,埋深400~600 m,受工作面采动影响,围岩变形量达1 500 mm,钻孔窥视得到的破坏区深度达到8 m以上[8]。甚至在一些浅部矿井,巷道出现了冲击地压、煤与瓦斯突出等动力灾害。受采动应力影响的回采巷道、或处于其他复杂构造应力条件下巷道通常处于非均匀应力场中[14],巷道围岩变形破坏严重,出现动力灾害的巷道也会伴随围岩的大范围破坏。但是在芬纳公式指导下,静水压力条件下巷道围岩塑性区深度很小,即使应力达到了目前开采水平不可能达到的极限水平且岩石参数和煤岩参数相当(强度较低),芬纳公式计算的塑性区范围仍然很小,可见静水压力的理论已无法指导受采动、构造等影响下非均匀应力场中的工程实践。
静水压力条件下的芬纳公式基于弹塑性理论经过严格推导所得,计算结果与数值模拟计算结果基本吻合,公式的准确性及可靠性较高。通过与数值模拟结果对比研究分析,芬纳公式计算得到的孔洞围岩塑性区形态为均匀分布在圆孔周围的圆环形,且在极限应力条件下塑性区范围仍然很小,与实际非均匀应力场中出现的非对称变形及围岩变形破坏严重的现场工程事实不符,静水压力条件下的理论公式已无法指导实际条件下非均匀应力场中的工程实践。
4.2 塑性区边界方程的可靠性分析
基于非均匀应力场中孔洞围岩塑性区边界方程近似解的计算方法,作者采用Visual Basic开发了非均匀应力场中圆孔围岩塑性区计算软件。首先通过非均匀应力场中圆孔围岩的弹性应力解求出圆孔周围各点的应力值,然后通过摩尔-库伦破坏准则判别圆孔围岩的弹塑性状态,应力条件达到强度准则标记为红色记为塑性区,没有达到强度准则记为弹性区。用计算软件用来探索理论公式与数值模拟计算下塑性区的形态演化规律,同时比较计算出的塑性区范围及塑性区形态变化规律。
图4为岩石岩性一定(仍选取上文中煤岩力学参数),最小围压为20 MPa,通过变化侧压系数来改变围岩受力状态得到的塑性区形态演化规律(理论计算与数值模拟对比结果)。由图4可得:λ=1时,为双向等压受力模型,塑性区边界为规则的圆形,数值模拟与理论计算的塑性区形态一致,理论计算范围较数值模拟计算范围小;侧压系数由1增大到1.8过程中,塑性区水平方向逐渐变窄(相对竖直方向),竖直方向逐渐变宽,塑性区边界最大半径在纵轴上最小半径在横轴上,塑性区边界形成类似椭圆的形状,数值模拟与理论计算的塑性区形态一致,理论计算范围较数值模拟计算范围偏小;λ增大到一定值后再继续增大时,边界最大半径位置由纵轴处逐渐移向纵轴两侧,塑性区边界轮廓呈现坐标轴处凹陷4个象限内凸出类似蝴蝶的形状,随着λ继续增大蝶形范围不断扩展但其形状特征不再发生变化。数值模拟与理论计算得到的孔洞围岩塑性区形态一致,塑性区形态演化规律完全一致,理论计算范围较数值模拟计算范围偏小。同时,理论计算与数值模拟对比结果表明,随着侧压系数由1逐渐增大,塑性区范围由线性增长逐渐变为类指数形式增长,
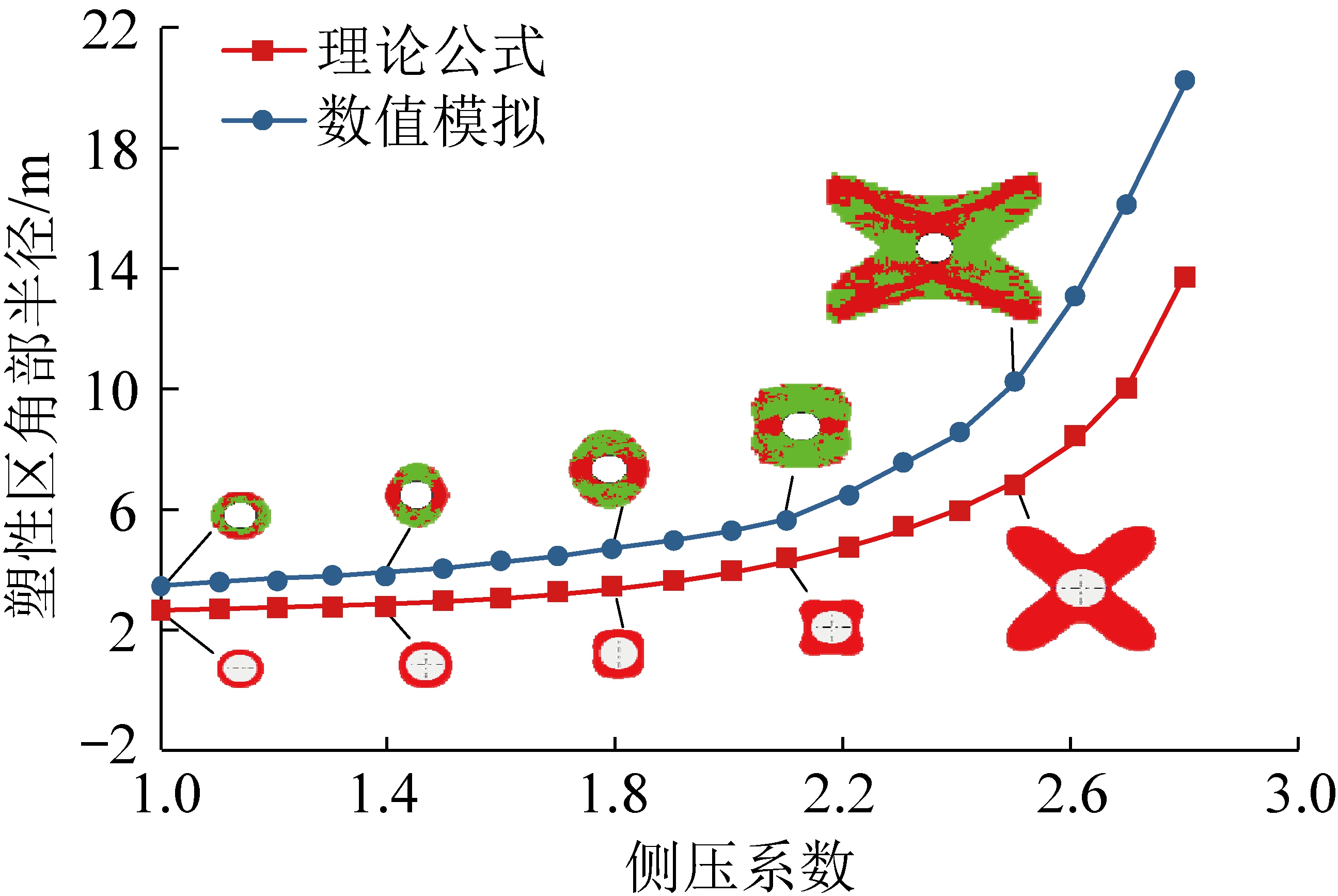
图4 非均匀应力场中圆孔围岩塑性区理论计算与数值模拟结果
Fig.4 Theoretical calculation and numerical simulation results of plastic zone of hole surrounding rock in non-uniform stress field
当塑性区形态变为蝶形时塑性区范围明显增大,图4中,应力水平20 MPa下侧压系数为2.5时塑性区范围已达到10 m,与工程现场非均匀应力环境中巷道、硐室的大范围破坏结果吻合,理论计算与数值模拟得到的蝶形非线性破坏规律一致。
塑性区边界近似方程没有考虑塑性应力的重新分布,实际上由于塑性应力的重新分布,应力会不断调整,围岩塑性区会不断扩大,所以理论计算结果较数值模拟计算结果在数值上偏小。但是理论计算与数值模拟得到的非均匀应力场中孔洞围岩塑性区形态一致,形态演化规律一致,蝶形非线性破坏规律一致,孔洞围岩塑性区边界方程近似解在计算塑性区范围大小时结果偏小,在研究非均匀应力场中孔洞围岩塑性区形态规律方面具有可靠性。
4.3 两个理论公式的适用性分析
侧压系数的大小反映了区域应力场不同方向应力大小的偏差程度,当侧压系数为1时为静水压力条件,随着侧压系数的增大偏应力水平不断提高。为了研究2个理论公式在不同应力场中的适用性,采用数值模拟方法研究了孔洞围岩塑性区在不同偏应力条件下的变化扩展规律,如图5所示。数值模拟仍然采用上文中的方形薄板受力模型,并采用与上文相同的岩石力学参数,最大水平应力从10 MPa加载到100 MPa,分别研究了不同偏应力环境下孔洞围岩塑性区随应力的变化规律。
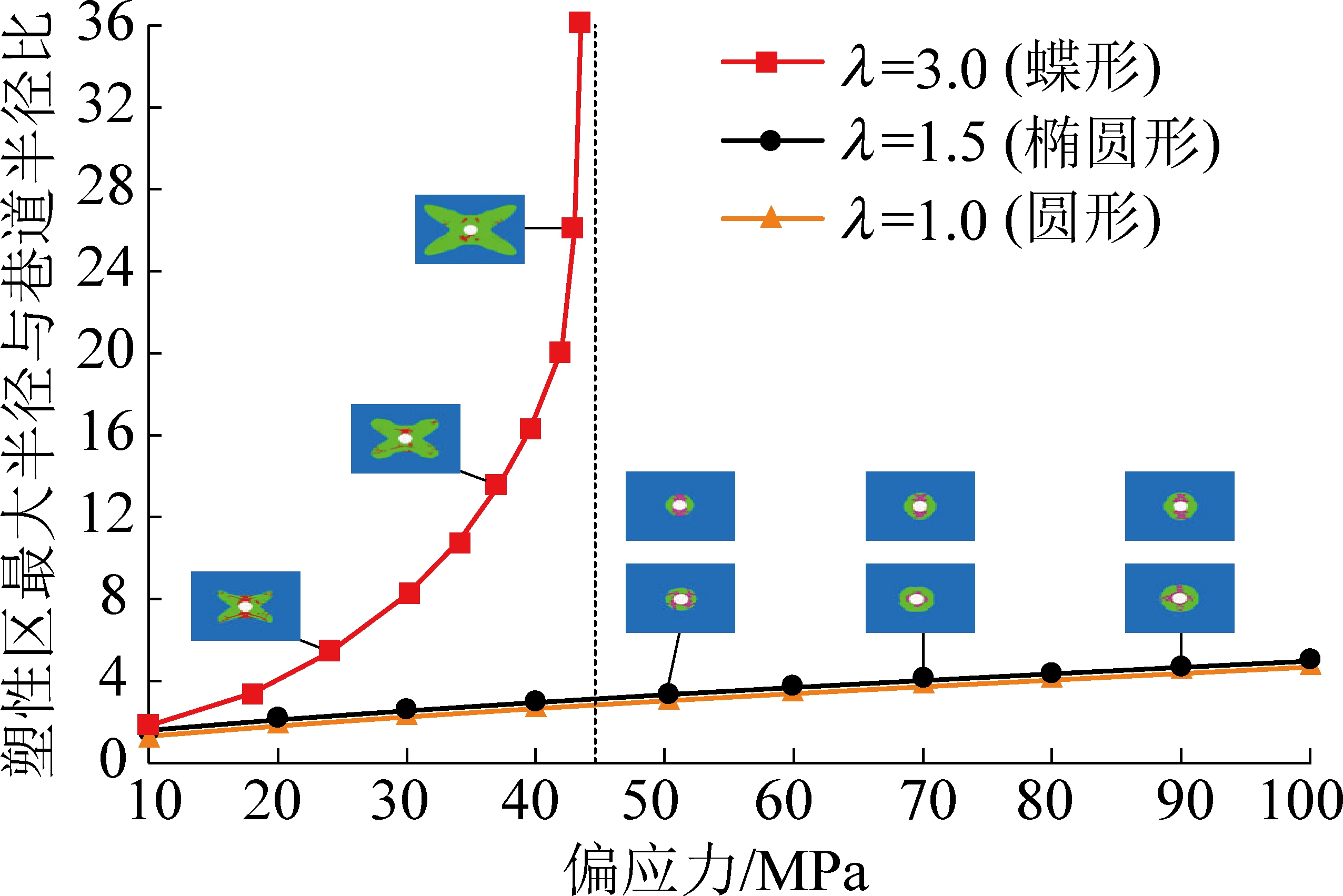
图5 不同受力方式下孔洞围岩塑性区扩展规律
Fig.5 Plastic zone expansion laws of hole surrounding rock under different loading modes
由图5可得,在相同的应力水平下不同的偏应力条件得到的塑性区形态及塑性区范围扩展规律完全不同。在静水压力及偏应力较低时(一般侧压系数小于2,图5采用了侧压系数为1.5的结果),塑性区形态表现为圆形或椭圆形,塑性区较均匀分布在孔洞周围,且在相同的应力水平下塑性区范围大小与静水压力下得到的范围相近,此时可以通过静水压力下得到的芬纳公式来计算塑性区范围;在偏应力较高时(一般侧压系数大于2,图5采用了侧压系数为3的结果),塑性区形态表现为蝶形,塑性区范围较大,且塑性区扩展表现出非线性规律。在非均匀应力场中,尤其是在偏应力水平较高的情况下,孔洞围岩塑性区形态、范围及扩展规律与静水压力条件下差异很大,静水压力条件下得到的芬纳公式已不适用于高偏应力环境。
非均匀应力场中孔洞围岩塑性区边界方程虽然为近似结果,但是可以很好地反映高偏应力环境中孔洞围岩塑性区的形态及扩展规律,已有文献基于塑性区边界方程理论指导,结合FLAC3D数值模拟,研究了非均匀应力场中巷道围岩的变形破坏规律及致灾机制,得到了许多有价值的结果。文献[8]首次提出了双向非等压条件下巷道围岩的蝶形不规则塑性区,阐述了蝶形塑性区的工程意义,并据此揭示了保德矿大变形回采巷道的非均匀冒顶机理;文献[15]在双向非等压条件下的塑性区理论计算中引入了偏应力分量,揭示了巷道围岩出现蝶形塑性区的力学本质;文献[16-17]系统研究了巷道围岩塑性区的一般形态,并给出了塑性区形态的判定准则及其数学表达式;之后将非均匀应力场中巷道围岩的蝶形破坏规律应用于巷道冲击地压及煤与瓦斯突出中[18-20],为巷道动力灾害的发生机理提供了新的思路。可见,非均匀应力场中孔洞围岩塑性区边界方程具有重要的理论价值及重大的工程指导意义。
通过以上内容的研究,静水压力条件下的芬纳公式以及非均匀应力场中孔洞围岩塑性区边界方程各具优势,也均存在一定的局限性,具有不同的适用条件。
1)在静水压力、近似静水压力及偏应力较小的条件下,孔洞围岩塑性区形态表现出圆形或椭圆形,其塑性区范围较小,在相同的应力水平条件下与静水压力得到的塑性区范围大小相近。静水压力下的理论公式推导过程严密,在塑性区范围计算精确度较高,适用于静水压力、近似静水压力及偏应力不高条件下围岩塑性区范围的计算。
2)在偏应力较高时,孔洞围岩塑性区形态将不再是圆形或椭圆形,且随着应力水平的增高,塑性区表现出非线性扩展规律;静水压力条件下得到的芬纳公式无论在塑性区形态还是扩展规律方面均不再适用。静水压力条件下得到的芬纳公式在研究高偏应力场中的工程问题方面不再适用。
3)孔洞围岩塑性区边界方程较数值模拟计算结果在塑性区尺寸上结果偏小,但是与数值模拟得到的孔洞围岩塑性区形态一致,塑性区形态演化规律一致,蝶形非线性破坏规律一致。相关研究成果显示,孔洞围岩塑性区边界方程在研究非均匀应力场中巷道围岩非对称大变形、巷道蝶形冒顶、巷道冲击地压、煤与瓦斯突出等问题中有重要的理论指导意义。孔洞围岩塑性区边解方程近似解适用于研究高偏应力场中地下空间围岩变形破坏规律及围岩稳定性分析。
5 结 论
1)静水压力条件下的芬纳公式及卡斯特奈公式推导过程严密,在静水压力条件或偏应力较小时计算的塑性区范围精度较高,适用于静水压力及偏应力较低条件下孔洞围岩塑性区范围的计算;当偏应力较大时,不能反映围岩的破坏规律,其将不再适用。
2)非均匀应力场中孔洞围岩塑性区边界隐性方程在公式推导过程中做了简化处理,得到的结果为近似解,计算的塑性区范围结果偏小,但是与数值模拟得到的孔洞围岩塑性区形态一致,塑性区形态演化规律一致,蝶形非线性扩展规律一致,能很好地反应高偏应力场中孔洞围岩塑性区形态演化规律,以及塑性区随应力增大出现的非线性扩展规律。孔洞围岩塑性区边界方程近似解适用于高偏应力场中地下空间围岩变形破坏规律研究及围岩稳定性分析。
3)煤矿井下受到采动影响及地质构造影响后,围岩将处在非均匀应力场中,处在其中的巷道、硐室通常会出现变形破坏严重、维护困难的情况,非均匀应力场中孔洞围岩塑性区边界方程对于研究此类巷道、硐室的变形破坏规律及致灾机制具有重要的理论价值及工程指导意义。
[1] 侯朝炯. 巷道围岩控制[M]. 徐州:中国矿业大学出版社,2013.
[2] 马念杰, 侯朝炯. 采准巷道矿压理论及应用[M]. 北京: 煤炭工业出版社, 1994.
[3] 钱鸣高,石平五.矿山压力与岩层控制[M].徐州:中国矿业大学出版社,2003.
[4] 郑颖人,朱合华,方正昌,等. 地下工程围岩稳定分析与设计理论[M]. 北京:人民交通出版社,2012.
[5] KASTNER H.隧道与坑道静力学[M].同济大学,译.上海:上海科学技术出版社, 1980:35-38.
[6] 于学馥,郑颖人,刘怀恒,等. 地下工程围岩稳定分析[M]. 北京:煤炭工业出版社,1983.
[7] 陈立伟,彭建兵,范 文,等. 基于统一强度理论的非均匀应力场圆形巷道围岩塑性区分析[J].煤炭学报,2007,32(1):20-23.
CHEN Liwei,PENG Jianbing,FAN Wen, et al. Analysis based on unified strength theory of non-uniform stress field circular roadway for plastic zone[J]. Journal of China Coal Society,2007,32(1):20-23.
[8] 赵志强.大变形回采巷道围岩变形破坏机理与控制方法研究[D].北京:中国矿业大学(北京),2014.
[9] 赵志强,马念杰,刘洪涛,等. 巷道蝶形破坏理论及其应用前景[J].中国矿业大学学报,2018,47(5):969-978.
ZHAO Zhiqiang, MA Nianjie, LIU Hongtao, et al. A butterfly failure theory of rock mass around roadway and its application prospect[J].Journal of China University of Mining and Technology,2018,47(5):969-978
[10] 马念杰,赵希栋,赵志强,等.深部采动巷道顶板稳定性分析与控制[J].煤炭学报,2015,40(10):2287-2295.
MA Nianjie,ZHAO Xidong,ZHAO Zhiqiang,et al.Stability analysis and control technology of mine roadway roof in deep mining[J].Journal of China Coal Society,2015,40(10):2287-2295.
[11] 俞茂宏. 双剪理论及其应用 [M]. 北京:科学出版社, 1998.
[12] 孟召平,彭苏萍,傅继彤,等.含煤岩系岩石力学性质控制因素探讨[J].岩石力学与工程学报,2002,21(1):102-106
MENG Zhaoping, PENG Suping, FU Jitong, et al. Study on control factors of rock mechanics properties of coal-bearing formation[J].Chinese Journal of Rock Mechanics and Engineering,2002,21(1):102-106.
[13] 贾后省,马念杰,朱乾坤.巷道顶板蝶叶塑性区穿透致冒机理与控制方法[J]. 煤炭学报,2016,41(6):1384-1392.
JIA Housheng, MA Nianjie, ZHU Qiankun. Mechanism and control method of roof fall resulting from butterfly plastic zone penetration[J].Journal of China Coal Society,2016,41(6):1384-1392.
[14] 赵志强,马念杰,郭晓菲,等. 大变形回采巷道蝶叶型冒顶机理与控制[J].煤炭学报,2016,41(12):2932-2939.
ZHAO Zhiqiang,MA Nianjie,GUO Xiaofei,et al.Butterfly-failure roof falling principle and support design of large deformation mining roadways[J].Journal of China Coal Society,2016,41(12):2932-2939.
[15] 马念杰,李 季,赵志强.圆形巷道围岩偏应力场及塑性区分布规律研究[J].中国矿业大学学报,2015,44(2):206-213.
MA Nianjie, LI Ji, ZHAO Zhiqiang. Distribution of the deviatoric stress field and plastic zone in circular roadway surrounding rock[J]. Journal of China University of Mining and Technology, 2015,44(2):206-213.
[16] 郭晓菲,马念杰,赵希栋,等.圆形巷道围岩塑性区的一般形态及其判定准则[J].煤炭学报,2016,41(8):1871-1877.
GUO Xiaofei, MA Nianjie, ZHAO Xidong, et al.General shapes and criterion for surrounding rock mass plastic zone of round roadway[J].Joumal of China Coal Society,2016,41(8):1871-1877.
[17] GUO Xiaofei, ZHAO Zhiqiang, GAO Xu, et al. Analytical solutions for characteristic radii of circular roadway surrounding rock plastic zone and their application[J]. International Journal of Mining Science and Technology,2019:263-272.
[18] 马念杰,郭晓菲,赵志强,等.均质圆形巷道蝶型冲击地压发生机理及其判定准则[J].煤炭学报, 2016,41(11):2679-2688.
MA Nianjie, GUO Xiaofei, ZHAO Zhiqiang, et al. Occurrence mechanisms and judging criterion on circular tunnel butterfly rock burst in homogeneous medium[J]. Journal of China Coal Society, 2016,41(11): 2679-2688.
[19] 赵志强,马念杰,郭晓菲,等.煤层巷道蝶型冲击地压发生机理猜想[J].煤炭学报,2016,41(11):2689-2697.
ZHAO Zhiqiang, MA Nianjie, GUO Xiaofei, et al. Mechanism conjecture of butterfly rock burst in coal seam roadway[J]. Journal of China Coal Society,2016,41(11):2689-2697.
[20] 马念杰,赵希栋,赵志强,等.掘进巷道蝶型煤与瓦斯突出机理猜想[J].矿业科学学报, 2017,40(4):137-149.
MA Nianjie, ZHAO Xidong, ZHAO Zhiqiang, et al. Conjecture about mechanism of butterfly-shape coal and gas outburst in excavation roadway[J]. Journal of Mining Science and Technology,2017, 40(4):137-149.
