0 引 言
大地电磁测深是利用天然电磁波穿透各种地层介质的能力不同而进行的地下结构探测方法,此方法以接收到的天然电磁波信号为载体,通过正、反演对地质构造进行解释,具有成本低、工作方便、不受高阻层的屏蔽、对低阻层的分辨率高、勘探深度大,等一系列优点,因此,此方法在理论研究和工业应用领域中均引起了极大的重视。但是,采集到的天然电磁波极易受各种场源、地质、人文等噪声干扰[1],是典型的非平稳、非线性信号。对大地电磁信号质量影响最严重的是长周期(方波噪声、三角波等)噪声,此类噪声主要存在于信号的低频、甚低频分段,噪声的振幅较强,在时域波形内将有效电磁信号完全淹没。若不能有效去除信号中的长周期噪声,会对地质构造解释造成严重的干扰甚至会出现错误的解释结果[2]。
为了有效抑制噪声对大地电磁信号的干扰,很多学者做出了深入的研究[3],例如,凌振宝[4]提出了利用多分辨小波阈值法去除大地电磁信号中的长周期噪声;蔡剑华等[5]将经验模态分解(EMD)率先应用到了大地电磁信号的去噪领域。大地电磁的有效信号分量多数集中在0~12 Hz,经验模态分解的噪声鲁棒性差,对噪声干扰严重的信号处理效果不理想,分解得到的本征模态分量频带混叠严重。小波变换在低频分段时域分辨率较低,导致小波分解无法有效处理大地电磁信号的长周期噪声。提高长周期噪声在信号低频分段的分辨率,是去除大地电磁信号中方波、三角波噪声的关键。通过研究天然电磁波中长周期噪声的性质,分析现有处理方法的不足,提出了多分辨VMD算法。
文献[6]中的VMD算法在2014年被提出,该方法为完全非递归分解模型运算,在获取分解分量的过程中,通过迭代搜寻变分模型最优解来确定每个模态分量的中心频率及带宽 [7],克服了EMD的模态混叠问题,突出了信号的局部特征,表现出更好的噪声鲁棒性,且具有良好的采样效应[8],该方法已在振动设备早期故障诊断领域成功应用。一次VMD处理得到的低频IMF分量长周期噪声分辨率低,包含着大量的有效电磁信号分量,多分辨VMD算法结合了多分辨分析和VMD算法的优点,能够对低频IMF分量进行多次分解处理,从而提高长周期噪声在低频分段的分辨率。对仿真和实测的大地电磁信号进行去噪处理,发现此方法对去除大地电磁信号中的长周期噪声有着一定的应用价值。
1 多分辨VMD算法
1.1 VMD算法原理
变分模态分解通过迭代的方式搜寻最优变分模型,确定模态分量的中心频率和频带宽度,实现每个模态分量的自适应剖分。若原输入信号为f(t),设定分解层数为K(正整数),变分模型约束表达式为[9]
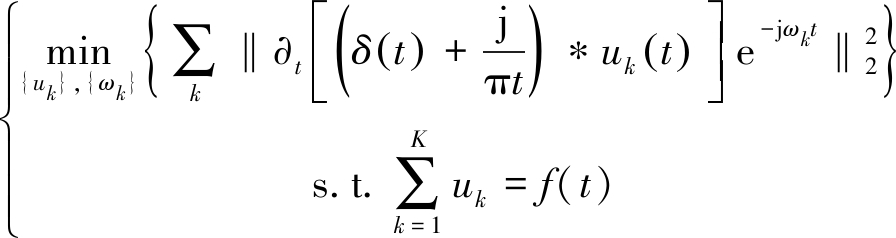
(1)
式中:uk为对应第k个IMF分量;ωk为对应第k个IMF分量的中心频率,其中k为正整数且k≤K;‖·‖2为二范数符号;∂t为对函数求时间t的偏导;δ(t)为单位脉冲函数;*为卷积运算符;j为虚数单位;![]() 为约束条件,即所有的IMF分量之和为原输入信号。
为约束条件,即所有的IMF分量之和为原输入信号。
引入Lagrange乘法算子σ更好地求解上述变分约束最优解,得到的增广Lagrange函数表达式如下[10]:
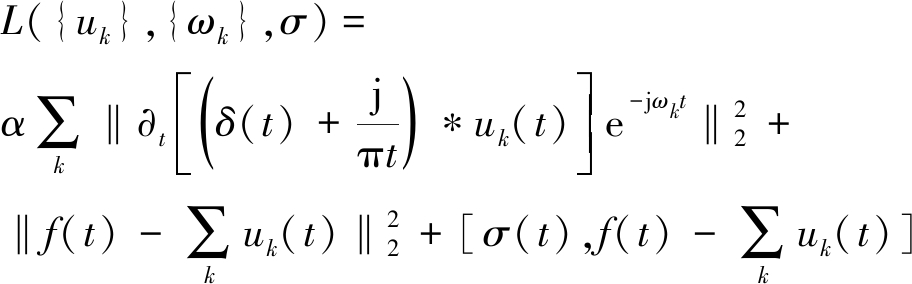
(2)
其中,α为二次惩罚因子,在受到高斯噪声影响下能够保障信号的重构精度;σ(t)使得约束条件保持严格性;VMD采用交替方向乘子法求取上述变分约束模型的最优解,从而将信号分解成K个IMF分量,其实现步骤如下[11]:
1) 初始化![]() 和循环步数n均为0,令n=n+1执行整个循环。
和循环步数n均为0,令n=n+1执行整个循环。
2)k=1、2、…、K,执行内层循环,更新![]() 和
和![]() 更新公式为[12-13]
更新公式为[12-13]
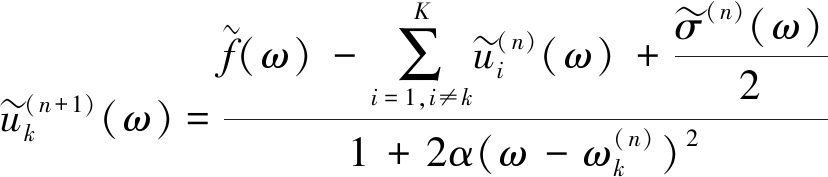
(3)
(4)
(5)
式中:τ为噪声容忍度,一般设置![]() 分别对应
分别对应![]() 的傅里叶变换。
的傅里叶变换。
3) 精度收敛判断:
设置精度![]() 时结束循环,输出最终的uk和ωk,否则返回步骤2)。
时结束循环,输出最终的uk和ωk,否则返回步骤2)。
1.2 VMD算法参数组合选取
VMD算法参数组合包括α和K,其中α决定了IMF分量的频带衰减速度,K决定了IMF分量的个数 [14]。随着α的增大,IMF分量的频带衰减速度越快,导致相邻IMF分量之间的有效部分会被过度去除。当α较小时,IMF分量之间会出现严重的频带混叠现象。研究表明:当α为2 000时VMD的自适应性最佳;K较小时会出现欠分解状态,无法将更多主要的信息分解到IMF分量中,K较大时会出现过分解状态,主要表现为多个IMF分量拥有同1个中心频率,在实际应用中K的选择集中在4~6。
综上所述,为了在提高分解分辨率的同时降低频带混叠的概率,在进行VMD处理时选择的α和K分别为2 000、5。
1.3 多分辨VMD算法
多分辨VMD算法能够对某一信号进行多层次分解从而提高信号的时频分辨率,如图1所示。
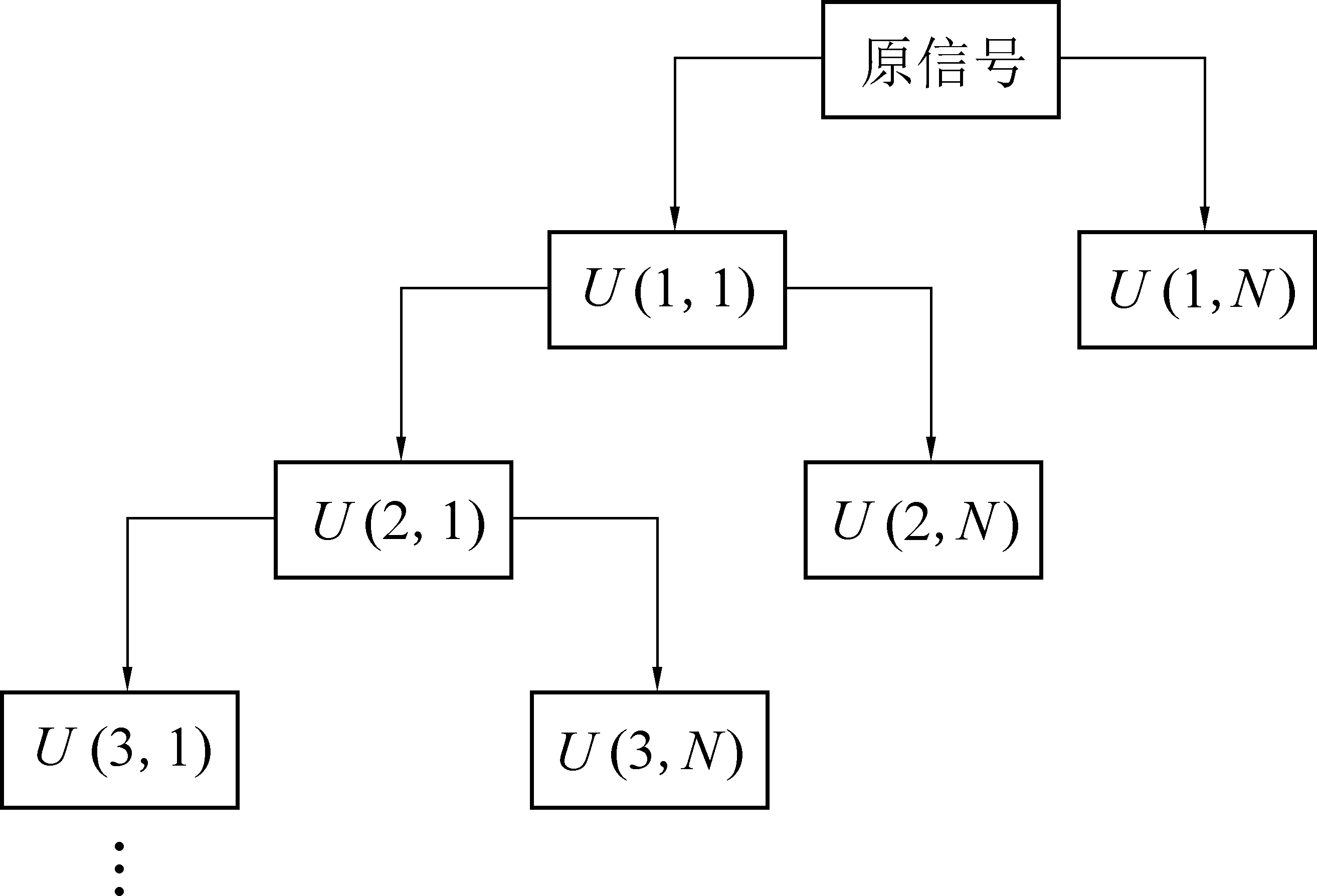
图1 多分辨VMD分解原理
Fig.1 Multiresolution VMD decomposition schematic
图1中,U(1,1)是原信号第1层VMD处理得到的低频IMF分量,U(1,N)表示第1层VMD处理得到的其他IMF分量,之后为提高长周期噪声的时频分辨率,对得到的低频IMF再次进行VMD处理,得到低频IMF分量U(2,1),以此类推,经过多次处理后,长周期噪声的时频分辨率逐渐提高。
2 仿真信号处理
选取0.01、0.05、0.1、0.5和1 Hz五个频率相叠加产生的正弦周期信号作为大地电磁的仿真信号,仿真信号的数学表达式如下:
f(t)=sin 0.02πt+sin 0.1πt+
sin 0.2πt+sin πt+sin 2πt
(6)
设置采样频率为30 Hz,采样时间为100 s。加入振幅不一、尺度不一的方波来模拟大地电磁信号中的长周期噪声。利用研究提出的去噪算法对含噪信号进行处理,去噪前、后时域波形如图2所示。
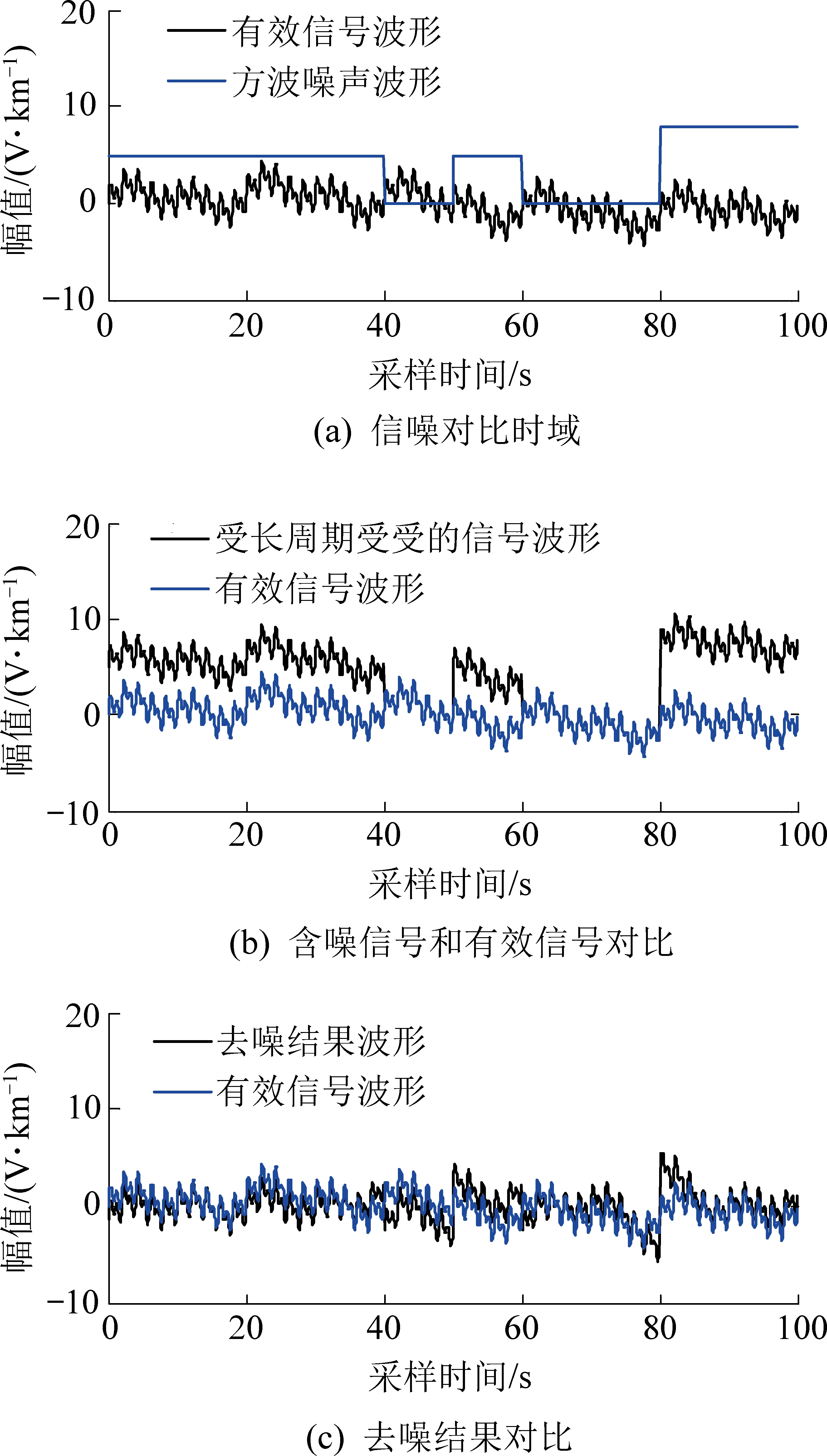
图2 仿真信号去噪对比
Fig.2 Comparison of simulated signal denoising
通过对比处理前、后的信噪比、均方根误差和相关系数来表征去噪的效果,见表1。
表1 三种评价标准对比
Table 1 Comparison of three evaluation criteria denoising

评价标准信噪比/dB均方根误差相关系数去噪前-10.15.00.49去噪后1.91.40.76
由图2知,图2a为有效信号和添加的方波干扰,图2b为有效信号与含噪信号的叠合对比,图2c为去噪结果与有效信号的对比。观察图2可知:去噪结果中的方波干扰得到明显抑制,信号的有效成分被很好的保留,去噪结果和有效信号的波形仅在方波干扰的上升沿附近有些许误差。表1分别给出了去噪前、后信号的信噪比、均方根误差和互相关系数。信噪比从-10.1 dB提升至1.9 dB,表明噪声得到了明显的抑制;均方根误差从5.0降至1.4;相关系数从0.49提升至0.76,表明去噪结果与原信号的相似度较高。从仿真处理的效果上来看,此方法可以用于实测大地电磁信号的处理中去。
3 实测信号处理
3.1 时域波形去噪结果
使用的实测数据是试验矿集区探测所得,探测数据为4道电磁数据;EX、EY、HX、HY,采样频率为24 Hz,截取1 000 s观测的数据作为处理对象, 首先使用多分辨VMD算法对原始电磁数据处理,设置处理层数为3层,其中EX的处理结果如图3所示。
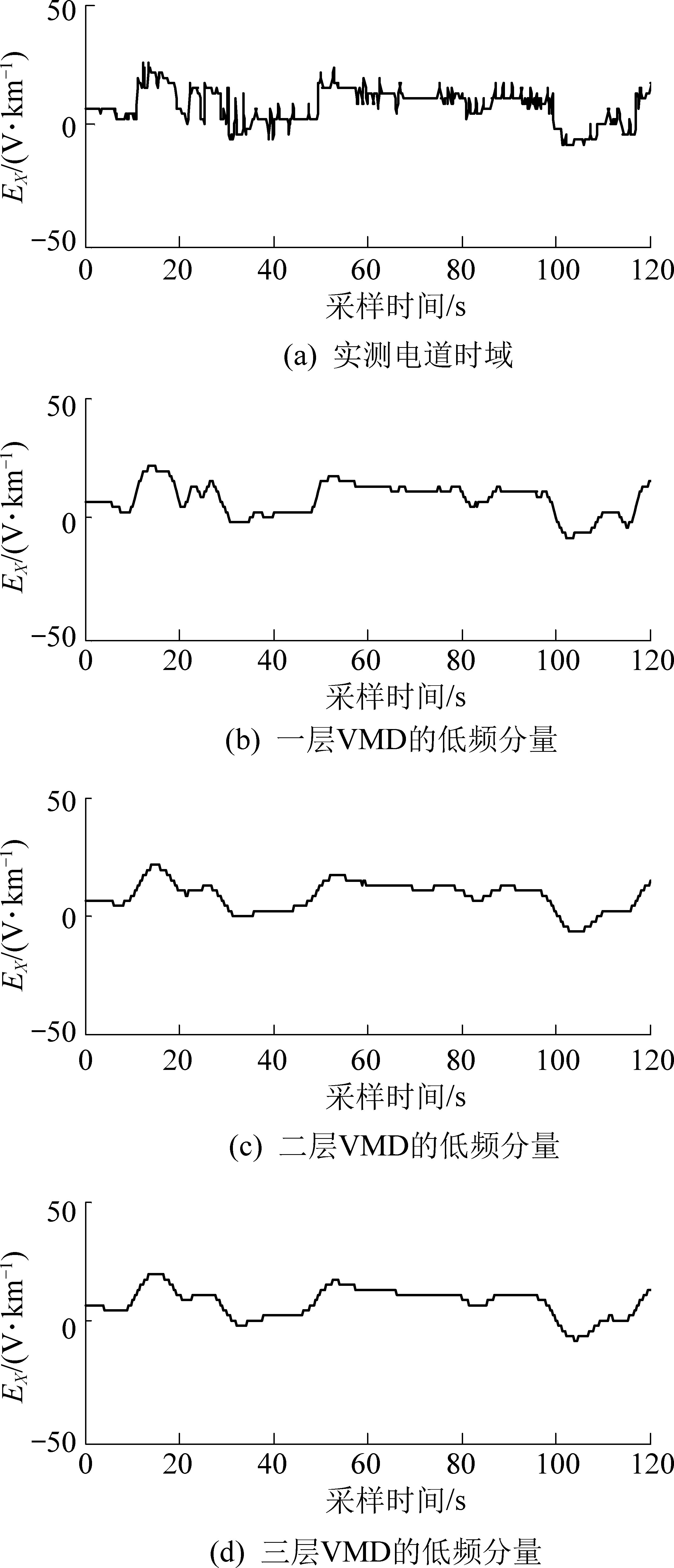
图3 多分辨VMD处理结果
Fig.3 Multi-resolution VMD processing results
去除最低频的IMF分量,4道电磁信号去噪前、后的时域波形分别如图4、图5所示,图6为去除掉的长周期噪声频谱。
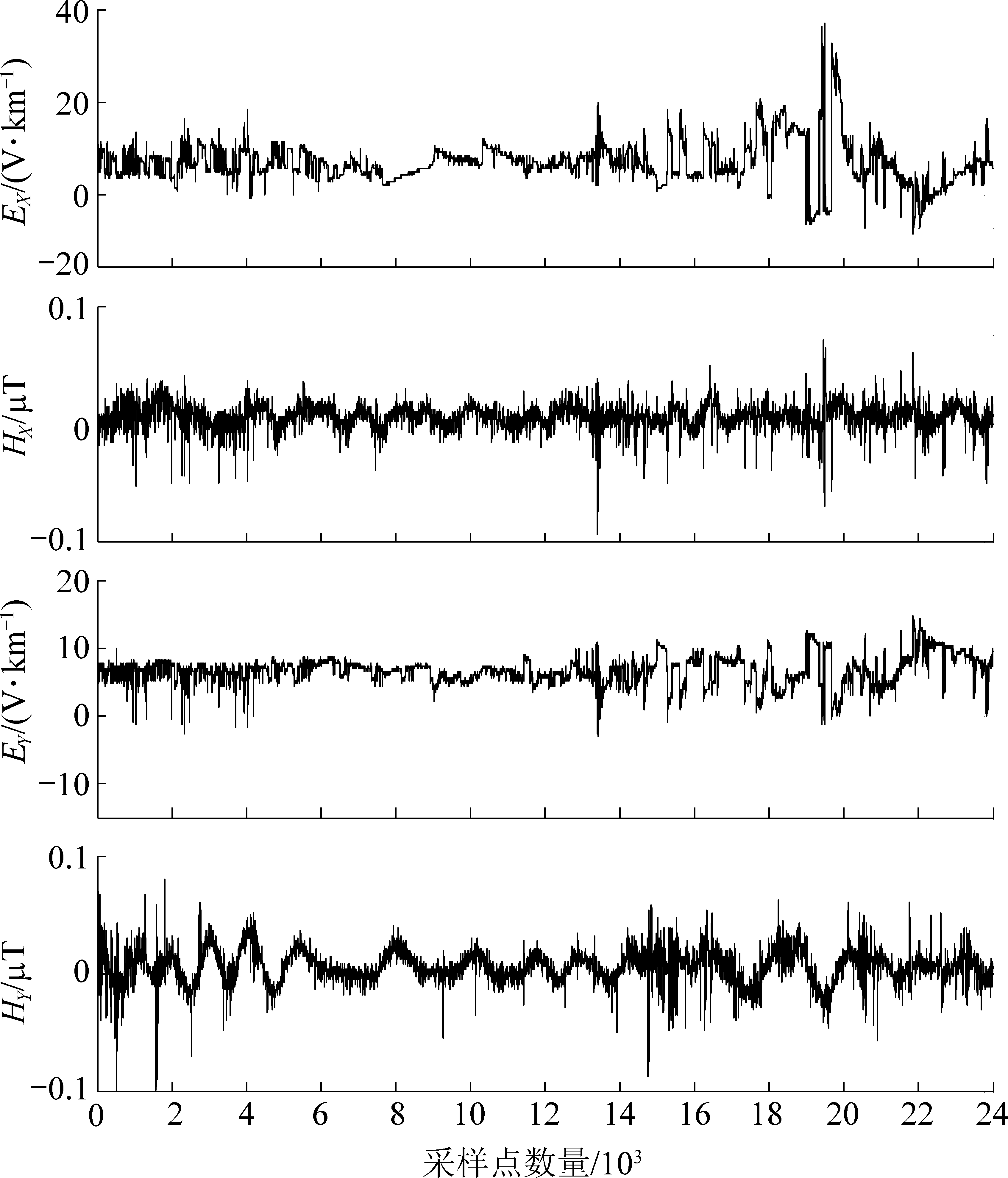
图4 实测信号的时域
Fig.4 Measured signal time domain
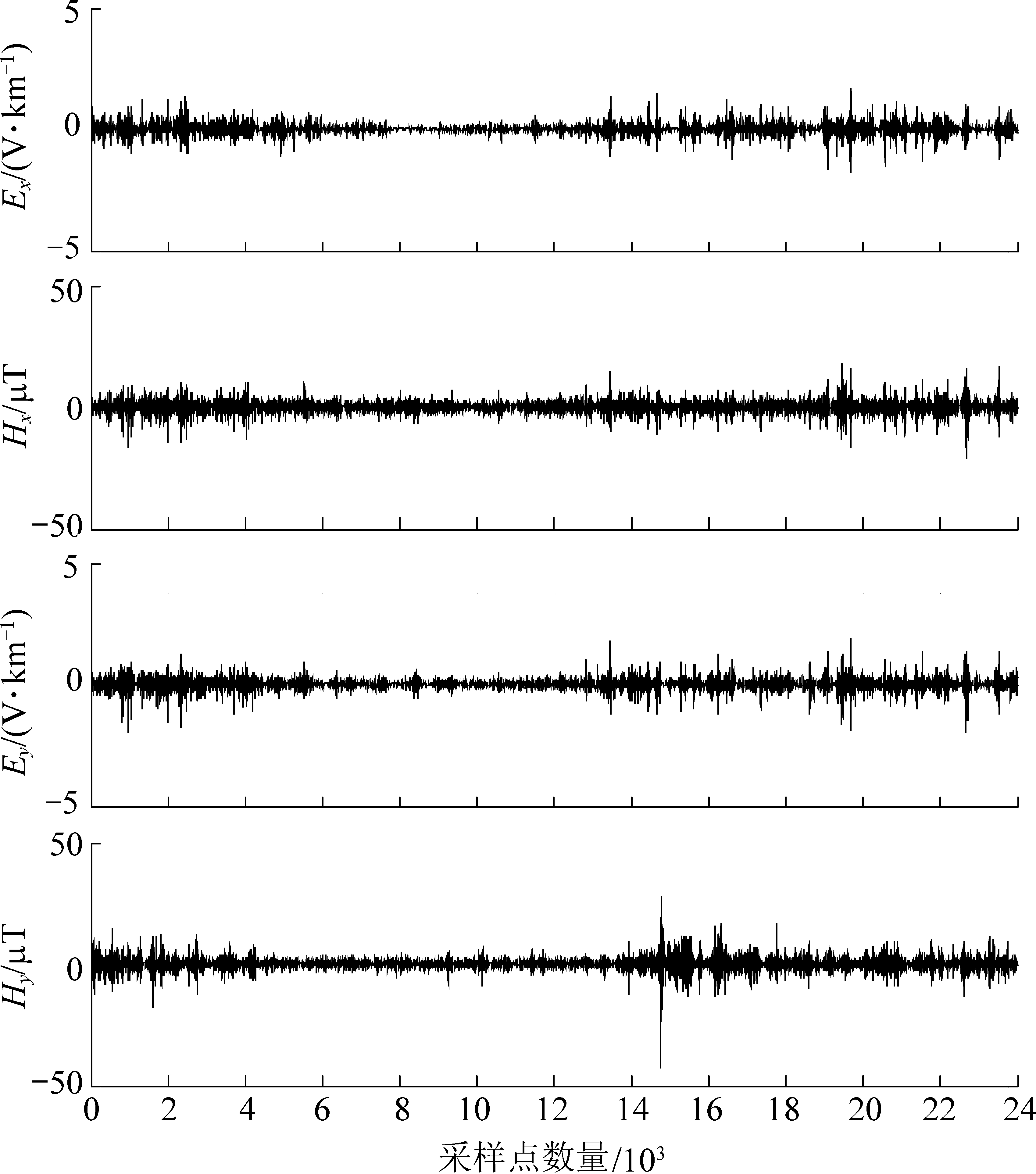
图5 实测信号去噪结果时域波形
Fig.5 Time domain waveform diagram after denoising of measured signals
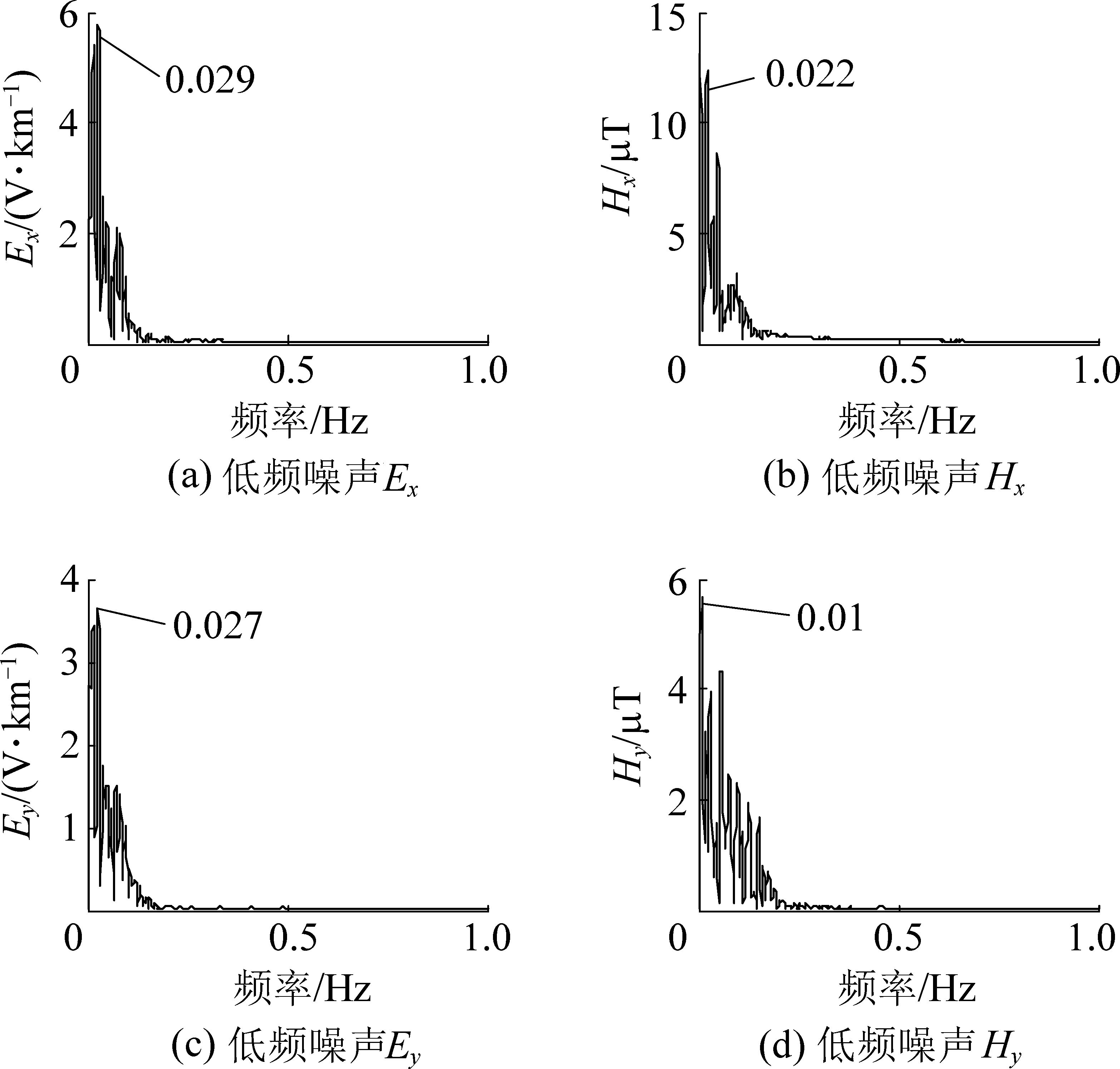
图6 长周期噪声频谱
Fig.6 Long-period noise spectrum
图3是使用多分辨VMD的处理效果图,其中图3a是原始电道信号,图3b为一层VMD分解得到的低频IMF分量。可以看出:此IMF分量包含了长周期方波噪声的同时也有一些低频有效分量,图3c、图3d分别为二层和三层VMD处理得到的低频IMF分量,随着处理层数的增加,得到的低频IMF分量的波形越光滑,这就说明包含的低频有效分量越少。
去噪前,信号受长周期噪声干扰严重,信号不稳定,信号的最值和均方根误差和去噪后相比较均有着较大的波动,有用的大地电磁信号被噪声淹没。去噪后,信号几乎没受到方波、三角波等长周期噪声的影响,在时域范围内变得更加平缓稳定,零点漂移现象得到有效改善。如图6所示:使用的多分辨分解方法在有效去除长周期噪声和高频噪声的同时仅对0.02 Hz左右的频率分量有较大的影响,对包含地层主要信息的0.1~10 Hz频带中的频率分量不会造成过度去除现象,去噪前、后的各个分量物理统计数见表2。
表2 去噪前、后信号各项指标比较
Table 2 Comparison of various indicators before and after denoising

评价指标Ex/(V·km-1)去噪前去噪后Hx/μT去噪前去噪后Ey/(V·km-1)去噪前去噪后Hy/μT去噪前去噪后最大值37.418.8132.375.436.725.014.813.3最小值-9.7-12.3-116.0-72.4-15.6-10.3-110.5-91.2均方误差/1036.12.417.610.817.13.0119.014.7
3.2 视电阻率-相位图
利用去噪前、后各个频点f的卡尼亚视电阻率和相位图曲线进行对比,进一步表征此方法的去噪效果,Royx与Roxy的卡尼亚视电阻率计算式为[15]
(7)
(8)
式中:FEx、FEy分别对应电道信号EX、EY的傅里叶变换;FHx、FHy对应磁道信号HX、Hy的傅里叶变换;ω为对应频点的弧度;ω=2πf,rad;μ为磁通率,μ=1×10-7 Wb/s。
去噪前、后的相位和视电阻率如图7、图8所示。由图7和图8可以看出,去噪后的视电阻率曲线更加平缓,尤其是在0.02~0.10 Hz内呈现缓慢下降的趋势,各频点的视电阻率没有出现较大幅度的畸变,虽然相位图在低频分段仍有少数频点跳变严重,但相对于去噪前已经得到了明显的优化。
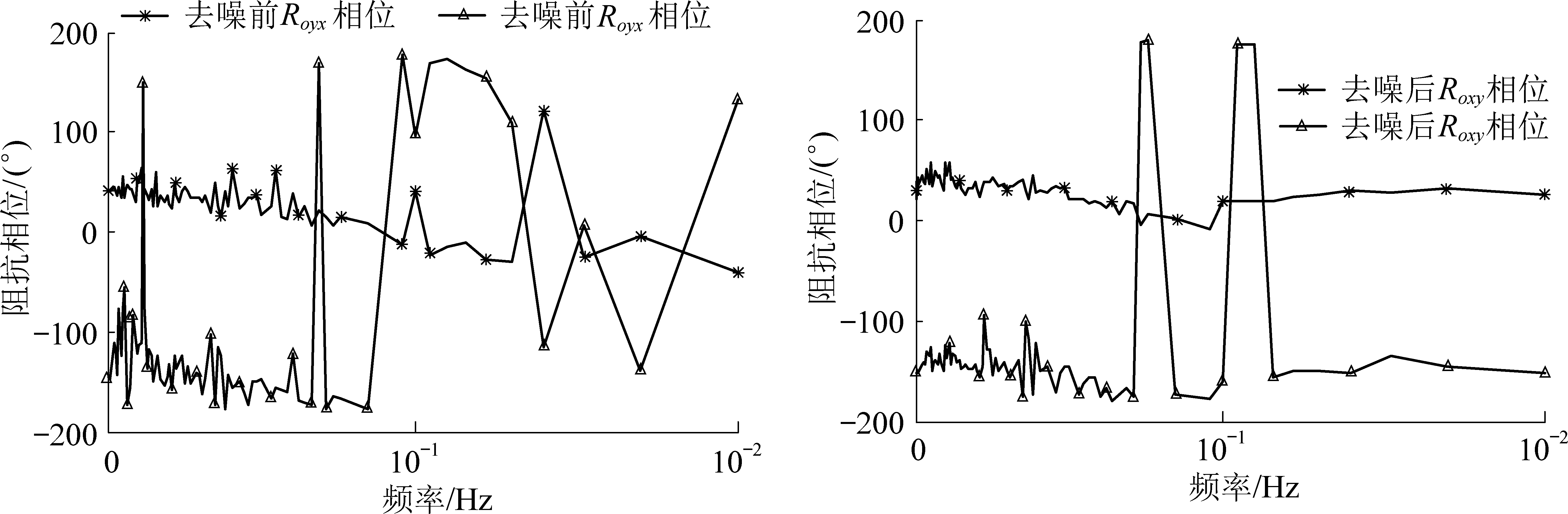
图7 去噪前、后相位对比
Fig.7 Phase contrast diagram before and after denoising
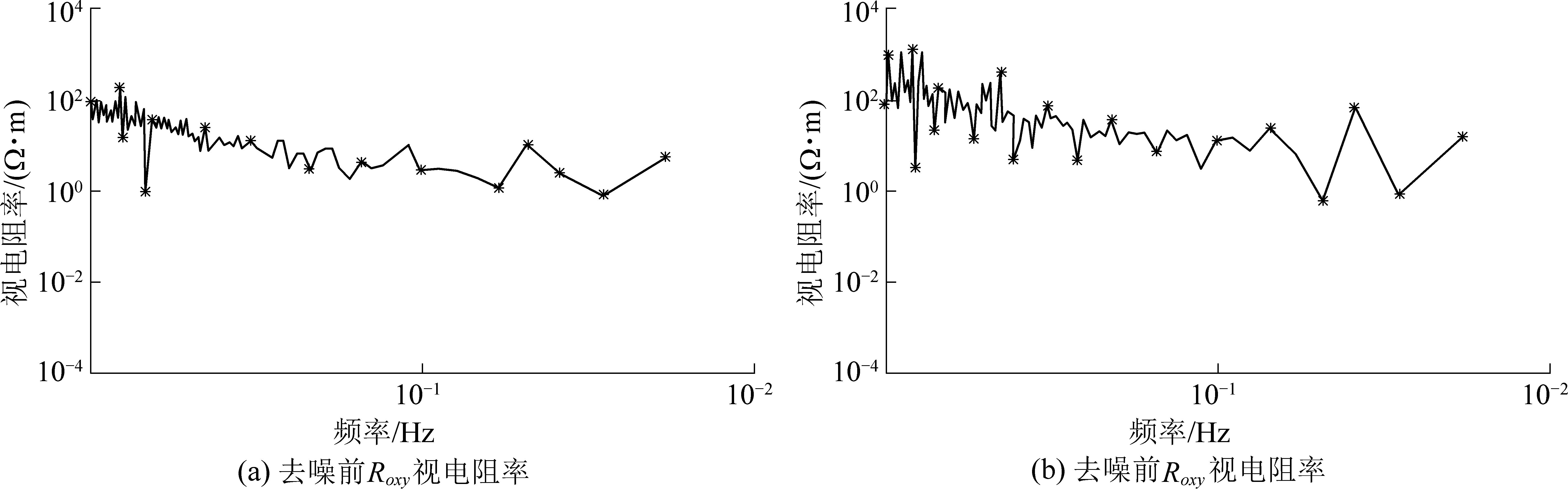
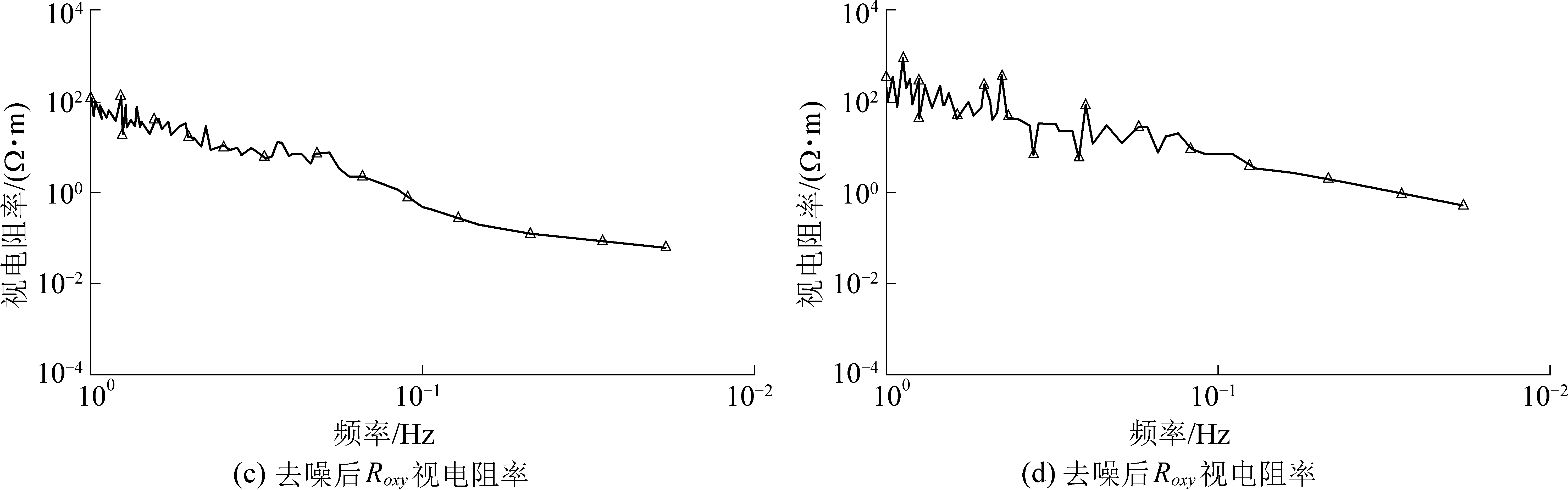
图8 去噪前、后视电阻率对比
Fig.8 Comparison of apparent resistivity before and after denoising
4 结 论
1)使用的数据分别为数值模拟试验得到的仿真电磁数据和在矿集区进行探测得到的大地电磁信号数据,数据均有着天然电磁信号受噪声影响的一般特性:电道信号主要受长周期方波干扰;磁道信号主要受长周期三角波影响。且长周期噪声的幅值比较大,将有效的大地电磁信号完全淹没。
2)多分辨VMD算法能够对大地电磁信号的低频、甚低频分段进行多层分解,提高长周期噪声在信号低频、甚低频分段的时频分辨率,之后根据长周期噪声的时频特点筛选出了包含长周期方波、三角波噪声的IMF分量。
3)使用多分辨VMD算法对仿真和实测大地电磁信号进行处理,去噪后的时域波形图周期性和平滑性显著增加,信号的最值和均方根误差有着一定的改善,低频分段的视电阻率和相位图曲线得到了明显优化。结果表明:此算法能够有效的去除大地电磁信号中的长周期噪声,提高低频分段视电阻率、相位的数据质量。
[1] 朱 威,范翠松,姚大为,等.矿集区大地电磁噪声场源分析及噪声特点[J].物探与化探,2011,35(5):658-662.
ZHU Wei,FAN Cuisong,YAO Dawei,et al. Field source analysis and noise characteristics of magneto telluric noise in ore district[J]. Geophysical and Geochemical Exploration,2011,35(5):658-662.
[2] 汤景田,化希瑞,曹哲民,等.Hilbert-Huang变换与大地电磁噪声压制[J].地球物理学报,2008,51(1):603-610.
TANG Jingtian,HUA Xirui,CAO Zhemin,et al. Hilbert-Huang transform and suppression of magnetotelluric noise[J].Chinese Journal of Geophysics,2008,51(1):603-610.
[3] 彭 冲,基于局域均值分解和小波阈值去噪的大地电磁数据处理[D].长沙:湖南师范大学,2016.
[4] 凌振宝,王沛元,万云霞,等.强人文干扰环境的电磁数据小波去噪方法研究[J].地球物理学报,2016,59(9):3436-3447.
LING Zhenbao,WANG Peiyuan,WAN Yunxia,et al. Research on wavelet denoising method of electromagnetic data in strong human interference environment[J]. Chinese Journal of Geophysics,2016,59(9):3436-3447.
[5] 蔡剑华.基于Hilbert-Huang变换的大地电磁信号处理方法与应用研究[D].长沙:中南大学,2010.
[6] 张俊甲,马增强,王梦奇,等.基于VMD与自相分析的滚动轴承故障特征提取[J].电子测量与仪器学报,2017,31(9):372-378.
ZHANG Junjia,MA Zengqiang,WANG Mengqi,et al. Fault feature extraction of rolling bearings based on VMD and self-phase separation analysis[J]. Journal of Electronic Measurement and Instrument,2017,31(9).372-378.
[7] 刘长良,武英杰,甄成刚.基于变分模态分解和模糊C均值聚类的滚动轴承故障诊断[J].中国电机工程学报,2015,35(13):1-8.
LIU Changliang,WU Yingjie,ZHEN Chenggang. Fault diagnosis of rolling bearing based on variational mode decomposition and fuzzy C-Means clustering[J]. Proceedings of the CSEE,2015,35(13),1-8.
[8] 贾亚飞,朱永利,王刘旺,等.基于VMD和多尺度熵的变压器内绝缘局部放电信号特征提取及分类[J].电工技术学报,2016,31(19):208-215.
JIA Yafei,ZHU Yongli,WANG Liuwang,et al. Feature extraction and classification of partial discharge signals in transformer internal insulation based on VMD and multi-scale entropy[J].Transactions of China Electrotechnical Society,2016,31(19):208-215.
[9] 马增强,李亚超,刘 政,等.基于变分模态分解和Teager能量算子的滚动轴承故障特征提取[J].振动与冲击,2016,35(13):134-139.
MA Zengqiang,LI Yachao,LIU Zheng,et al. Faultfeature extraction of rolling bearing based on variational mode decomposition and Teager energy operator[J].Journal of Vibration and Shock,2016,35(13):134-139.
[10] 唐贵基,王晓龙.参数优化变分模态分解方法在滚动轴承早期故障诊断中的应用[J].西安交通大学学报,2015,49(5):73-81.
TANG Guiji,WANG Xiaolong.Application of parameter optimization variation mode decomposition method in early fault diagnosis of rolling bearings[J].Journal of Xi'an Jiaotong University,2015,49(5):73-81.
[11] 王振威. 基于变分模态分解的故障诊断方法研究[D].秦皇岛:燕山大学,2015.
[12] 于生宝,何建龙,王睿家,等. .基于小波包分析和概率神经网络的电磁法三电平变换器故障诊断方法[J].电工技术学报,2016,31(17):102-111.
YU Shengbao,HE Jianlong,WANG Ruijia,et al. Fault diagnosis method of electromagnetic three-level converter based on wavelet packet analysis and probabilistic neural network[J].Transactions of China Electrotechnical Society,2016,31(17):102-111.
[13] 蒋伶俐,刘义伦,李学军,等.小波包去噪与改进HHT微弱信号特征提取[J].振动测试与诊断,2010,30(5):510-514.
JIANG Lingli,LIU Yilun,LI Xuejun,et al.Wavelet packet denoising and improved HHT weak signal feature extraction [J]. Vibration Testing and Diagnosis,2010,30(5):510-514.
[14] 王 刚,王书民,朱 威,等. AMT近源干扰压制方法[J].物探与化探.2015,39(2):371-375.
WANG Gang,WANG Shumin,ZHU Wei,et al.AMT near-source interference suppression method [J]. Geophysical and Geochemical Exploration,2015,39(2):371-375.
[15] 李肃义,林 君,阳贵红,等.电性源时域地空电磁数据小波去噪方法研究[J].地球物理学报,2013,56(9):3145-3152.
LI Suyi,LIN Jun,YANG Guihong,et al. Research on wavelet denoising method of electromagnetic source time domain electromagnetic data in time domain [J]. Chinese Journal of Geophysics,2013,56(9):3145-3152.
