0 引 言
增大钻孔直径可以增大施工后形成的卸压范围[1]、增大孔内暴露面积,从而提高瓦斯的抽采效率,也可减少钻进工程量[2]。钻孔抽放瓦斯一直是治理煤与瓦斯突出最常用的有效手段[3-5],已在淮南矿业集团和晋煤集团等开始进行推广应用[6-7]。但受井下条件限制,一次完成大直径钻孔施工存在困难,目前普遍采用多级扩孔的施工方法,即完成小直径先导孔施工后,提出钻杆钻头,然后换成扩孔钻头和螺旋钻杆,进行扩孔作业[8-11]。但是这种施工方法存在辅助钻进时间长,排渣困难,成孔效率低,且易发生钻孔偏斜,保直性差,影响后续下管作业等缺点,特别是当钻孔直径较大时,孔内煤渣多,且不易排出,不但影响扩孔轨迹,而且容易造成孔内事故。
为了解决大直径钻孔施工存在的上述问题,开发了回拉扩孔钻进工艺,研制了一套拆装式大直径钻头+扶正器+外平钻杆的组合钻具,进行回拉扩孔钻进工艺施工[12],该装备及工艺不但具有扩孔速度快和钻孔保直性好等优点,而且大大降低了工人的劳动强度,施工效率相比牙轮钻头得到了明显提升,满足顺槽联络巷大直径钻孔施工要求,取得了良好的应用效果。但是,该方法需要在目的巷道通过人工更换大直径钻头和扶正器进行回拉扩孔,因而仅适用于两巷道联通钻孔施工,对于普通非联络巷等不能适用。
针对非两巷道贯通大直径钻孔成孔存在的需要多次提钻,施工效率低,钻孔轨迹难以控制的问题,笔者设计了可开闭的ø300/153 mm连杆式回拉扩孔钻头,通过调节泥浆泵流量的方法,使得钻头处于关闭或者打开状态:即在正常钻进中能保持闭合,不影响正常钻进,在钻进至设计孔深时,通过增加泥浆泵流量方式,推动钻头内活塞运动从而带动切削刀翼旋转张开,在回转的同时向后提拉钻具,实现回拉扩孔。
1 回拉扩孔钻头结构及原理
ø300/153 mm连杆式回拉扩孔钻头结构如图1所示,回拉扩孔钻头主要由钻头钢体、切削刀翼、活塞、连杆、复位弹簧、上接头、下接头和销钉等零部件构成。上接头上端通过螺纹与钻杆相连,下端与钻头钢体连接,钻头钢体内部有活塞活动腔,活塞下安装有复位弹簧,保证切削刀翼能够在钻井液压力变小后保持闭合状态,同时也保证出现卡钻等事故后自动收回。活塞底部和2个连杆通过销钉相铰接,可相对活塞自由转动,连杆的另一端与切削刀翼相连接,可将活塞的轴向运动转换为切削刀翼的旋转运动。切削刀翼和钻头钢体之间通过销钉相连接,钢体下端和下接头相连接,下接头可通过螺纹连接先导孔钻头。
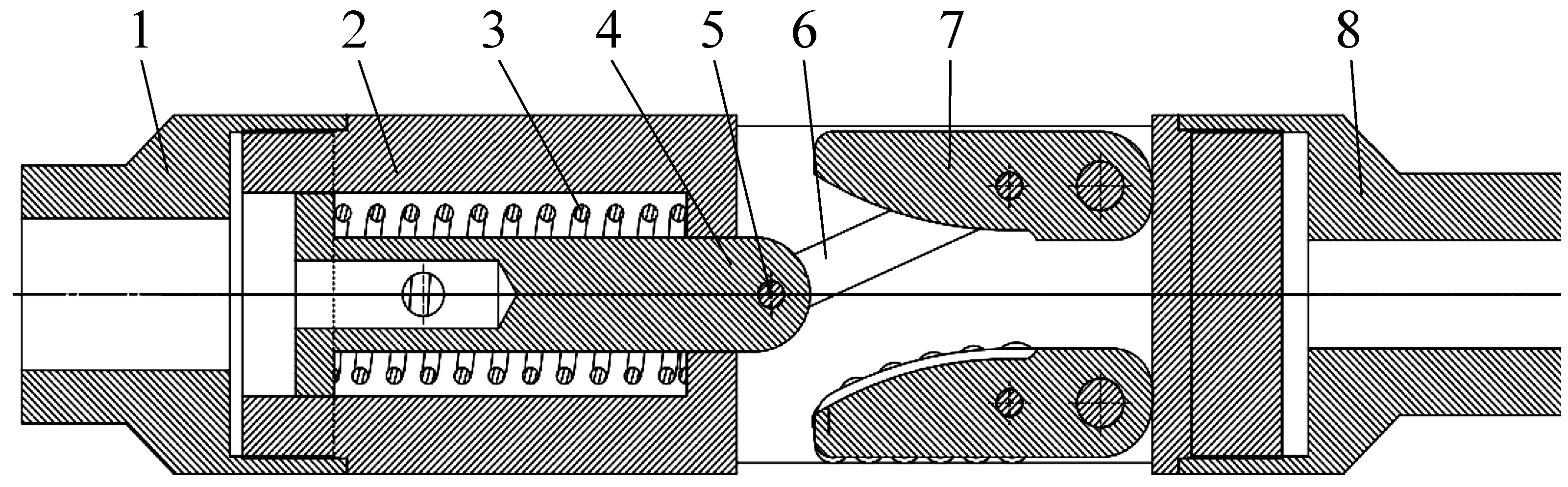
1—上接头;2—钻头钢体;3—复位弹簧;4—活塞;5—销钉;6—连杆;7—切削刀翼;8—下接头
图1 回拉扩孔钻头结构示意
Fig.1 Structural sketch of back reamer
正常钻进时,由于水压较小,钻井液作用于活塞的推力不足以克服弹簧的预紧力,活塞不能沿轴向移动,2个刀翼均保持闭合状态,可进行先导钻孔施工。当完成钻孔钻进作业需要进行回拉扩孔时,增大泥浆泵的流量,钻井液作用于活塞的推力大于弹簧的预紧力从而推动活塞沿轴向向前移动,切削刀翼逐渐张开。至切削刀翼与孔壁接触时,开始进行造穴,当切削刀翼和钢体成90°夹角时,为切削刀翼张开到最大位置,可以进行回拉扩孔作业。当扩孔作业完成时,关闭泥浆泵,活塞在复位弹簧的作用下沿着轴向退回,切削刀翼亦缩回至钢体内,对提钻作业不产生影响。
钻进过程中,切削刀翼的打开和闭合状态切换是否灵敏可靠,关系到回拉扩孔钻头的设计和应用能否成功。当切削刀翼张开小于45°时,切削刀翼张开主要靠水压推动活塞,当切削刀翼张开角度大于45°时,水压产生的推力还没有达到平衡状态,切削刀翼继续张开,直到张开到90°。若出现水压力不够的情况,钻机施加一定的拉力,切削刀翼可以轻松打开,保证了回拉扩孔时,切削刀翼能顺利张开。
2 开闭机构力学分析
ø300/153 mm回拉扩孔钻头开闭机构可简化为曲柄滑块机构,如图2所示。其中,图2a和图2b分别为刀翼闭合和张开位置时的机构。当滑块处于最远位置时,要求曲柄与滑块运动轴线平行;当滑块处于最近位置时,要求曲柄垂直于滑块运动轴线。翼片张开过程中避免了曲柄和连杆共线,故不会出现死点位置[13]。
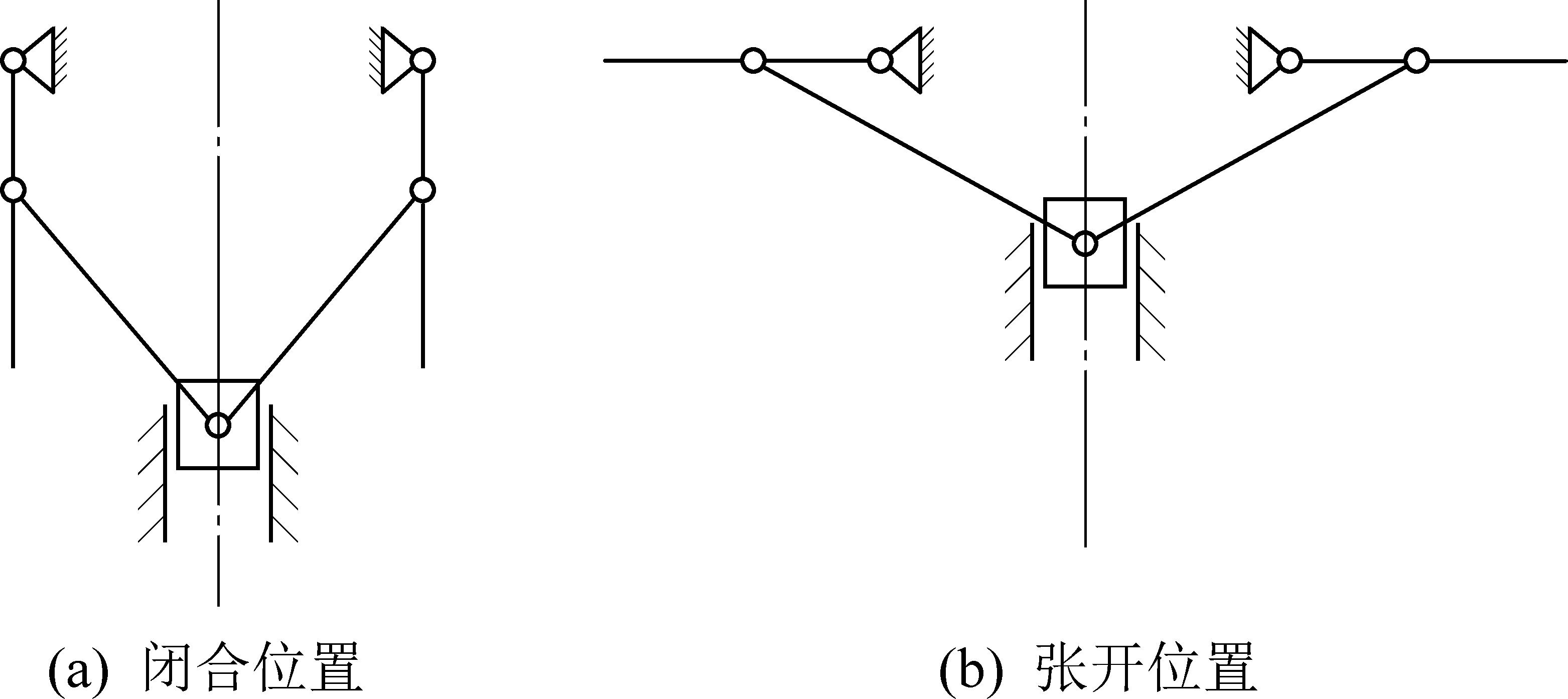
图2 极限位置时机构示意
Fig.2 Structure sketch of mechanism at extreme position
切削刀翼处于一般位置的状态如图3所示,其中:α为切削刀翼张角;β为连杆张角;L为连杆长度;e为偏心距;b为曲柄长度;h为连杆铰支点与刀翼铰支点之间的轴向距离;M为活塞对刀翼的推动力矩。
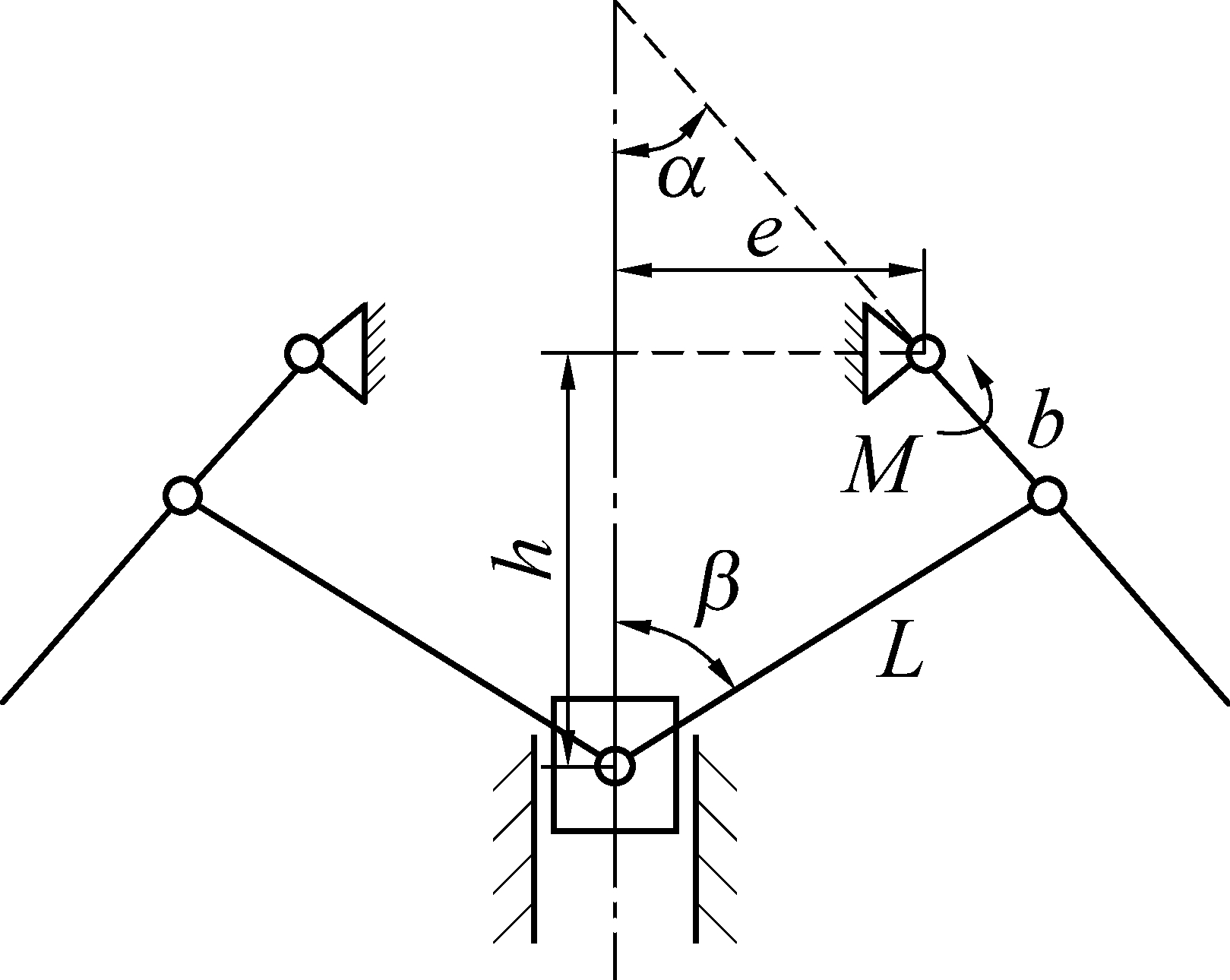
图3 一般位置时机构示意
Fig.3 Schematic sketch of mechanism in general position
忽略连杆与滑块、连杆与刀翼、刀翼与铰支座之间的摩擦力矩以及滑块与侧壁之间的摩擦阻力。以活塞作为受力分析对象,如图4所示,根据平衡原理可知:
F=2FLcos β
(1)
式中:F为活塞所受推力;FL为连杆对活塞作用力。
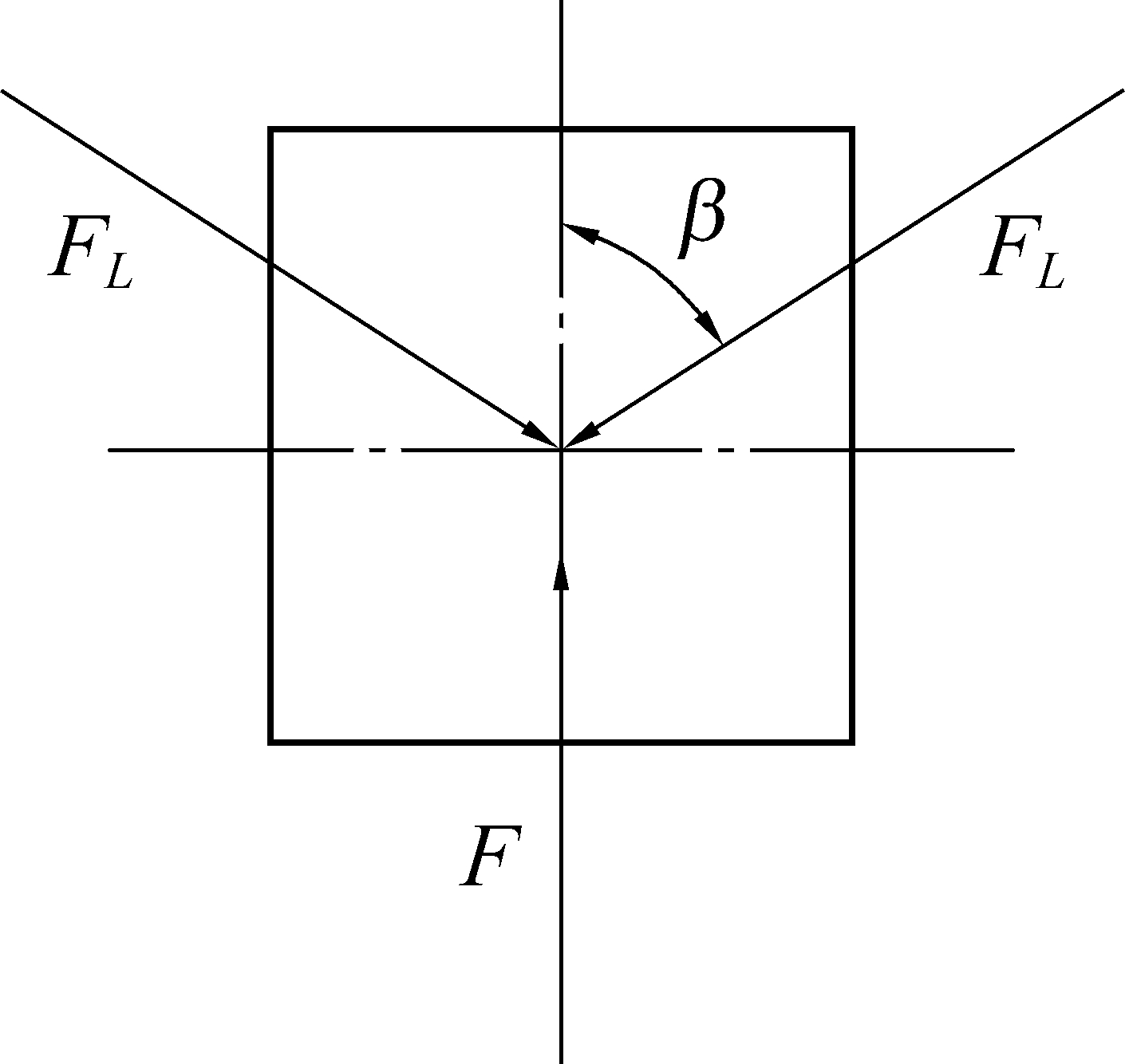
图4 活塞受力情况
Fig.4 Force condition of piston
活塞对刀翼的推动力矩为
M=FLbsin (α+β)=FLlf
(2)
定义lf为活塞的推力传递到曲柄而对刀翼的等效力臂,由式(1)、式(2)得
lf=[b(sin α+cos αtan β)]/2
(3)
由连杆与铰支座位置的几何位置关系,可得
Lsin β=bsin α+e
(4)
联立式(1)—式(4)得
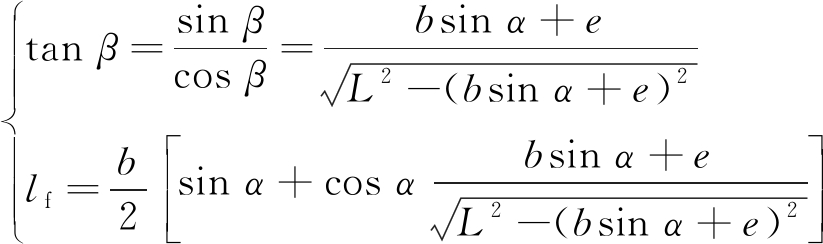
(5)
因此,在活塞推力一定的情况下,刀翼所受力矩M(α,b,L,e)与切削刀翼张角α、曲柄长度b、连杆长度L和偏心距e等因素有关。
3 最佳传力性能张开机构尺寸的确定
3.1 偏心距及活塞行程的确定
由式(5)可知,为保证较好的传力性能,应该选取较大的偏心距e。实际中,钢体的直径为132 mm,正常钻进成孔的尺寸为153 mm,考虑到铰支座与钻头钢体的强度,实际取e=40 mm。
活塞行程影响翼片张开灵敏程度:活塞的行程过大,会导致切削刀翼张开过于缓慢,影响张开效果;活塞行程过小,则切削刀翼张开过于灵敏,对复位弹簧的要求较高。虑到钻头轴向尺寸及翼片空间限制,确定的活塞行程为65 mm。
3.2 最佳传力性能连杆及曲柄长度的确定
回拉扩孔钻头张开机构应保证切削刀翼张角α在0°~45°时具备足够的张开力矩[14]。考虑到α和β的实际意义,切削刀翼从闭合到张开的过程中α和β都是单调增加的。从切削刀翼初始闭合(α=0)到张开至与切削刀翼与连杆垂直(α+β=90°)位置,对于任意1组固定的偏心距e、连杆长度L和曲柄长度b的组合,由式(2)可得出M(α)为增函数,即切削刀翼张开的过程中所受的推动力矩是逐渐增加的。在此过程中,最小推动力矩出现在切削刀翼将要张开的初始位置(α=0)。此时,切削刀翼所受推动力矩M0 为
M0=Feφ(b,L)
(6)
其中,![]()
活塞的行程S可表示为
(7)
连杆长度L与曲柄长度b的数值关系可通过隐函数(7)来获得。由式(7)可得
(8)
当活塞行程S=65 mm时,连杆长度L与曲柄长度b的关系如图5所示。
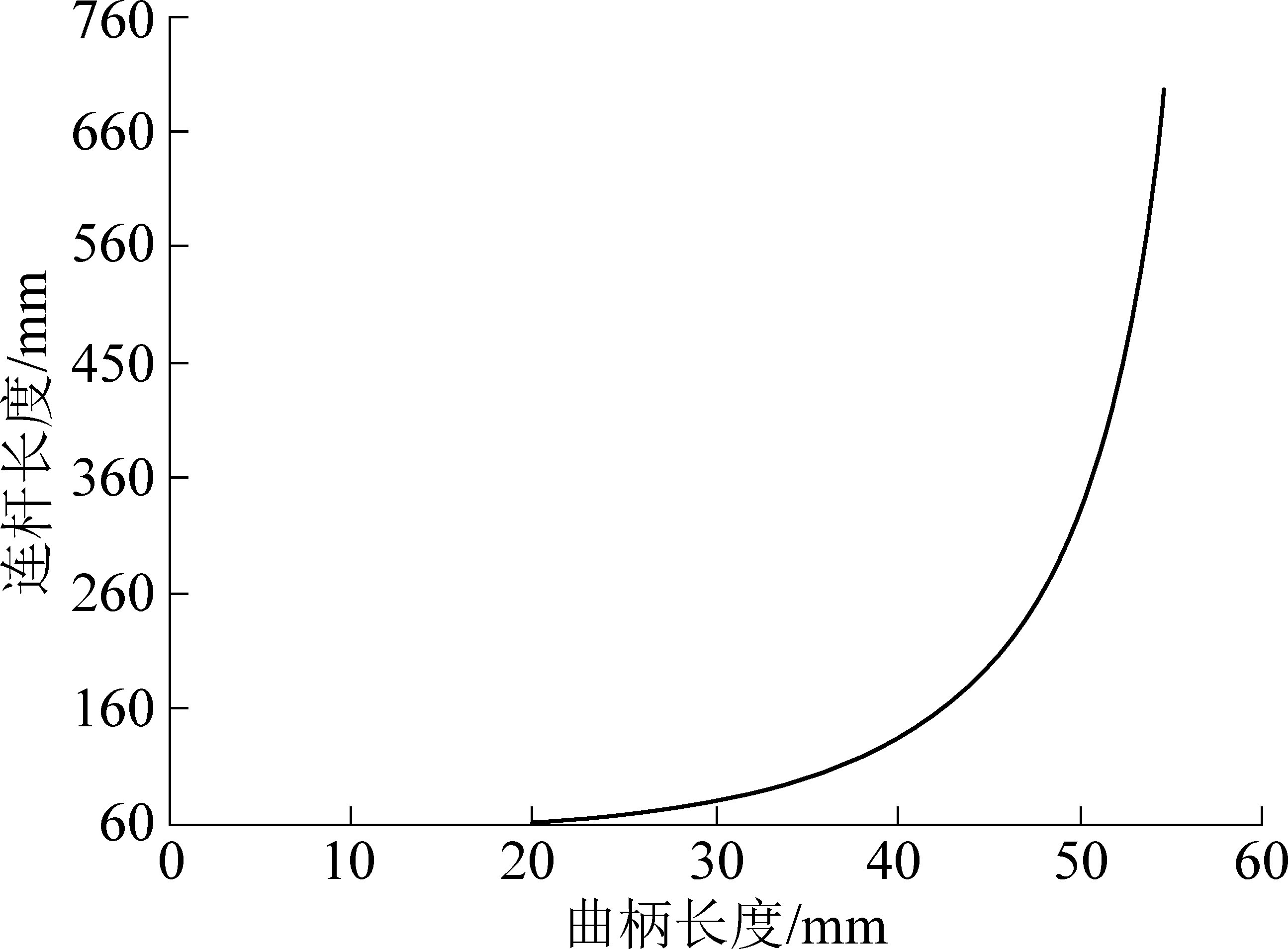
图5 连杆长度L与曲柄长度b的关系
Fig.5 Relationship between connecting rod lengthL and crank length b
在式(8)条件下,函数φ(b,L)与曲柄长度b的关系如图6所示。由图6可知,b=26 mm时,φ(b,L)取得极大值。根据式(7)可算出L=72 mm,由此得到连杆和曲柄长度组合使得刀翼具有初始最大推动力矩。
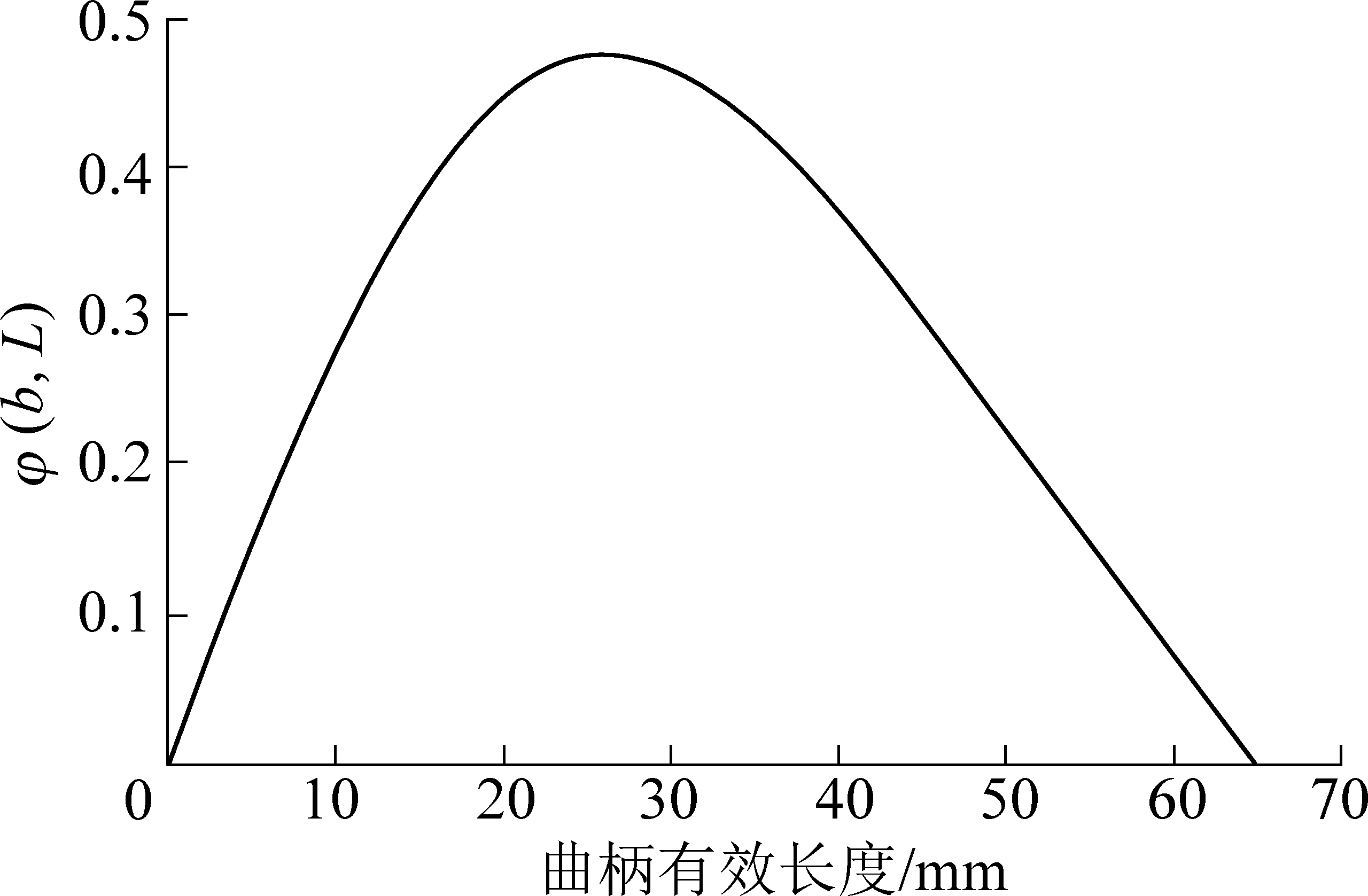
图6 曲柄长度与φ(b,L)关系
Fig.6 Relationship between connecting rod length and φ(b,L)
由上述方法确定的活塞行程以及连杆和曲柄长度组合,刀翼受到的等效力臂随切削刀翼张角的变化趋势如图7所示。可看出,切削刀翼在张开过程中,受到的推动力矩呈现先增大后减小的趋势。推动力矩最小值出现在刀翼的初始位置(张角为0°),最大值出现在张角为56°位置处。
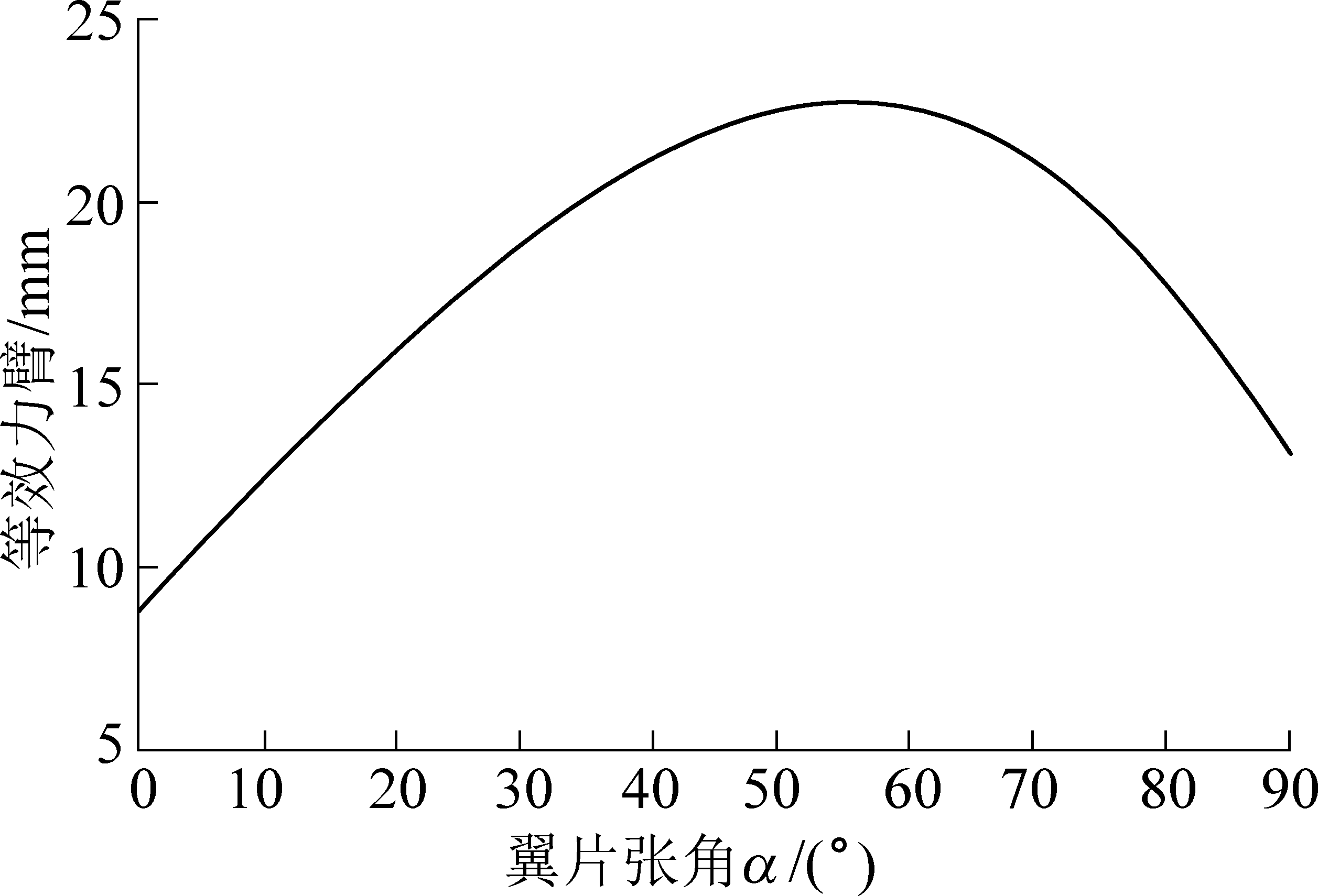
图7 切削刀翼张角与等效力臂关系
Fig.7 Relationship between blade tension angle and equivalent force arm of cutting tool
4 复位弹簧选型设计
复位弹簧的设计选型主要为控制初始预紧力和最大压紧力。初始预紧力至少应大于正常钻进时水流对活塞的推力;最大压紧力不宜过大或过小:过大会使刀翼张开阻力过大,过小则会影响刀翼的快速复位。受回拉扩孔钻头空间结构限制,所确定的上接头内孔直径为56 mm,活塞中心孔的直径为25 mm,钢体钻孔的直径为16 mm,切削刀翼未张开活塞台肩与壳体活塞台肩的距离为100 mm。
4.1 水流对活塞的推力分析
正常钻进时,水压产生的压力差不足以克服弹簧的预紧力,切削刀翼处于闭合状态,此时活塞未沿轴向移动,设计的水通过扩孔钻头的路线为上接头—活塞—钢体钻孔—下接头如图8所示。对上述的水路图经简化后如图9所示,水通过活塞孔最终流出,可认为是自由水射流模型[15-16]。水流对活塞的作用力包括水流对活塞的台肩的冲击力FR1和水流从两侧流出时对活塞的冲击力FR2,水流对活塞的推力为
FT=FR1+FR2
(9)
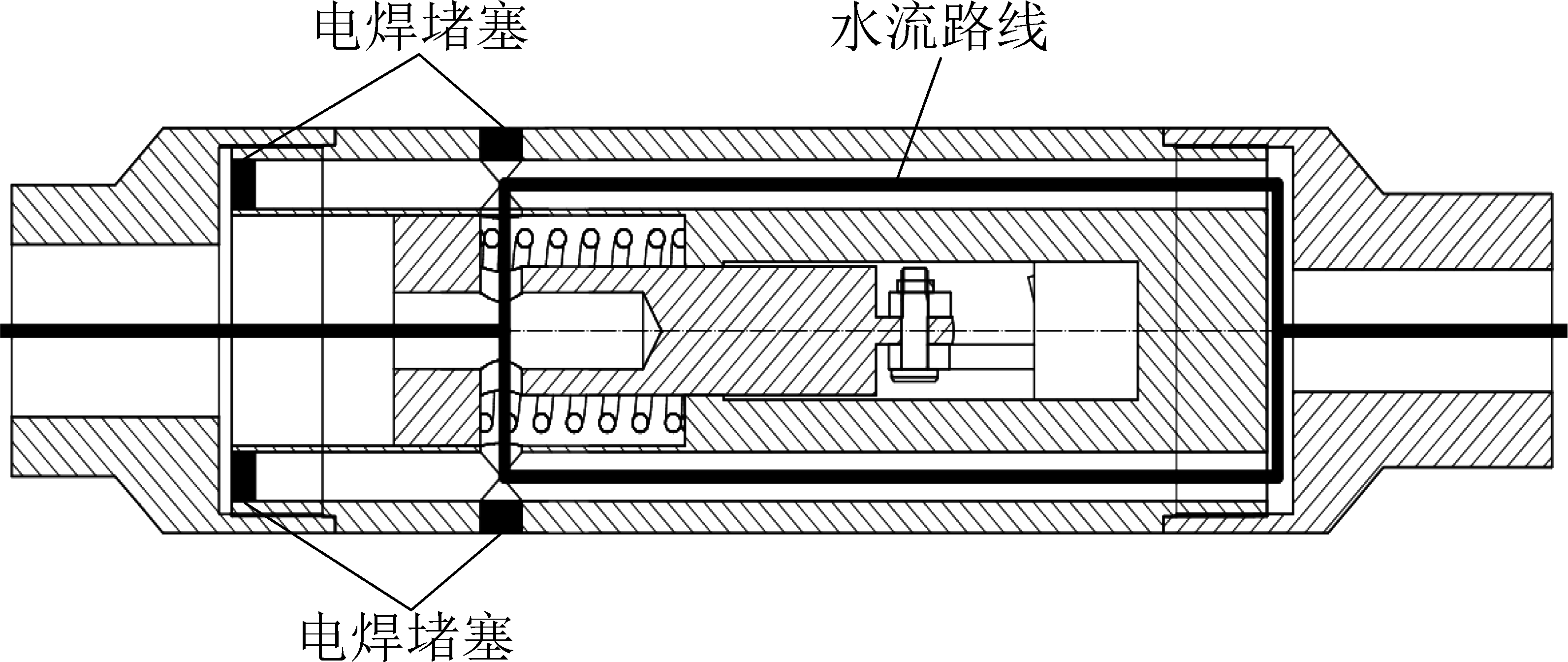
图8 正常钻进时水路
Fig.8 Waterways for normal drilling
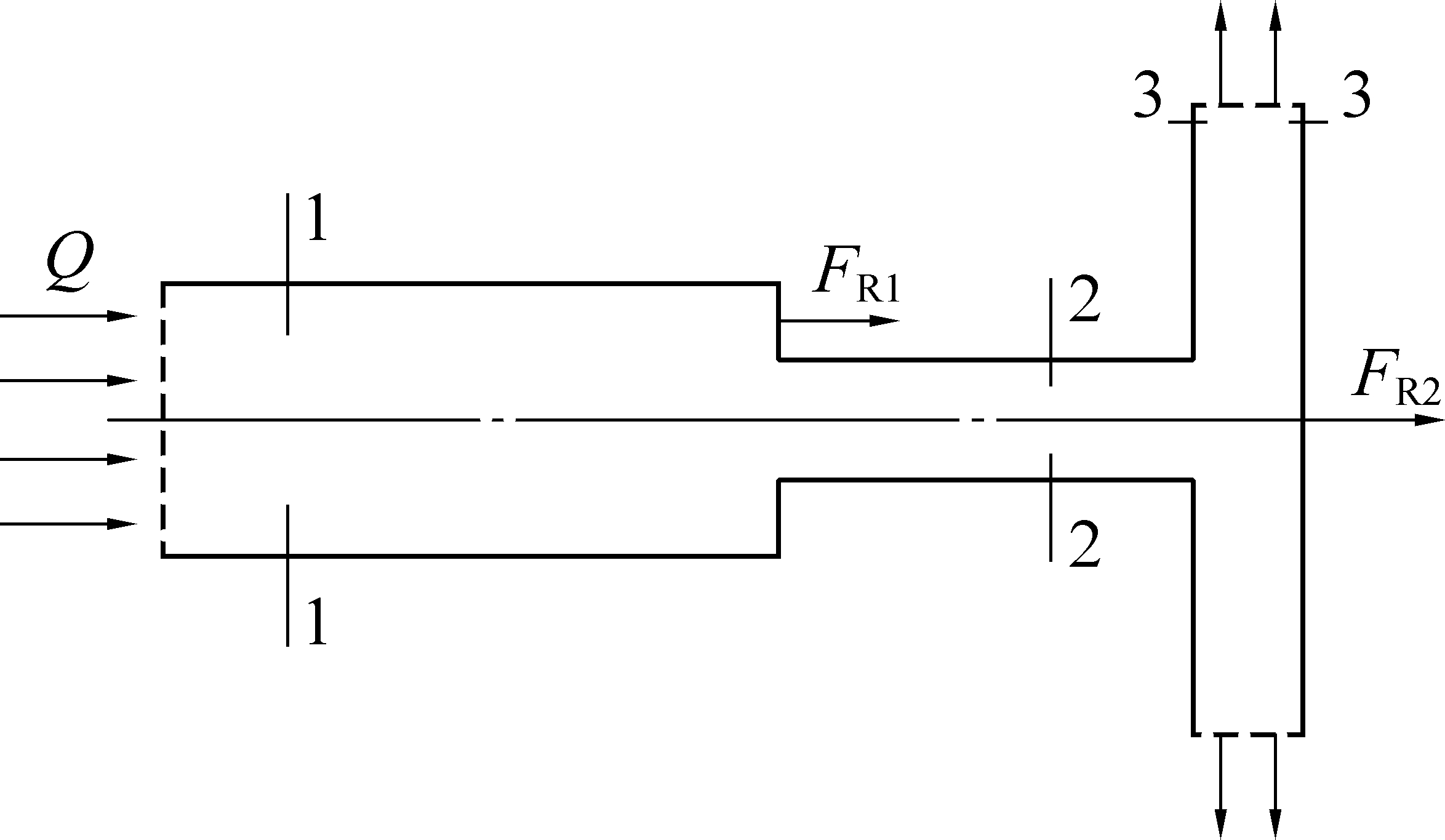
图9 正常钻进时流体力学示意
Fig.9 Fluid mechanics sketch for normal drilling
入水口流量为Q,忽略水势能变化和水头损失,分别取截面1-1、2-2之间和截面2-2、3-3之间控制体,伯努利方程为[17-20]
(10)
(11)
式中:p1、p2、p3分别为截面1-1、2-2、3-3处的压强;v1、v2、v3分别为截面1-1,2-2和3-3处流体的流速;ρ为流体密度。
连续性方程为
(12)
式中:d1、d2和d3分别为截面1-1、2-2、3-3的直径。
截面3-3为自由流出,故p3=0。由式(11)、(12)可得
(13)
将截面1-1水流流向取为X方向,截面1-1、2-2 之间控制体的动量方程为
(14)
将截面2-2水流流向取为X方向,截面2-2、3-3之间控制体的动量方程为
(15)
现场试验所用的泥浆泵量控制由泥浆泵档位确定,由2个档位控制钻头的开合,即2档(149 L/min)时,钻头保持闭合,既能满足正常钻进时所需水量,又不能将钻头切削刀翼张开。当泵量达到3档及以上时(泵量194~300 L/min)时,钻头切削刀翼张开进行回拉扩孔钻进。因此,可根据泥浆泵的临界流量计算水流对活塞的推力范围,以此作为依据进行复位弹簧选型设计。取正常钻进时泥浆泵的流量为160 L/min,迫使切削刀翼张开的泥浆泵的最大流量为300 L/min,根据式(10)—式(15)可算出,正常钻进时水流对活塞的推力为38 N、泥浆泵达到最大流量时水流对活塞的推力为137 N。
4.2 复位弹簧设计计算
弹簧在一般载荷条件下工作,可选用第三类弹簧,所使用的材料为50CrVA,其许用剪切应力[τ]和切变模量G分别为750 MPa和80 000 MPa。
受回拉扩孔钻头空间结构尺寸限制,所确定的弹簧中径D为60 mm,弹簧最大压缩量l2为40 mm,初步选取弹簧钢丝直径d为4 mm。根据泥浆泵达到最大流量时水流对活塞的推力计算结果,取初始弹簧压缩的弹力为38 N、最大压缩时弹簧所受的压力为120 N。
1)曲度系数K和钢丝直径d计算公式分别为
(16)
(17)
式中:C为弹簧指数;F″为最大压缩时弹簧的弹力。
2)弹簧刚度kF为
(18)
式中:F′为弹簧初始压缩时的弹力; l1为弹簧初始压缩时的高度;l2为弹簧最大压缩时的高度。
3)弹簧圈数n为
(19)
4)弹簧总圈数n0为
n0=n+2
(20)
5)弹簧节距p′为
(21)
其中,δ为弹簧钢丝间距。
6)弹簧自由长度l0为
l0=nδ+(n0-0.5)d
(22)
7)弹簧的螺旋升角αl和展开总长L0 分别为
(23)
(24)
取旋绕比C=6,最大变形时相邻两弹簧钢丝间距δ=10,由式(24)及相关校验公式计算并经标准化得出弹簧的工作原理如图10所示。
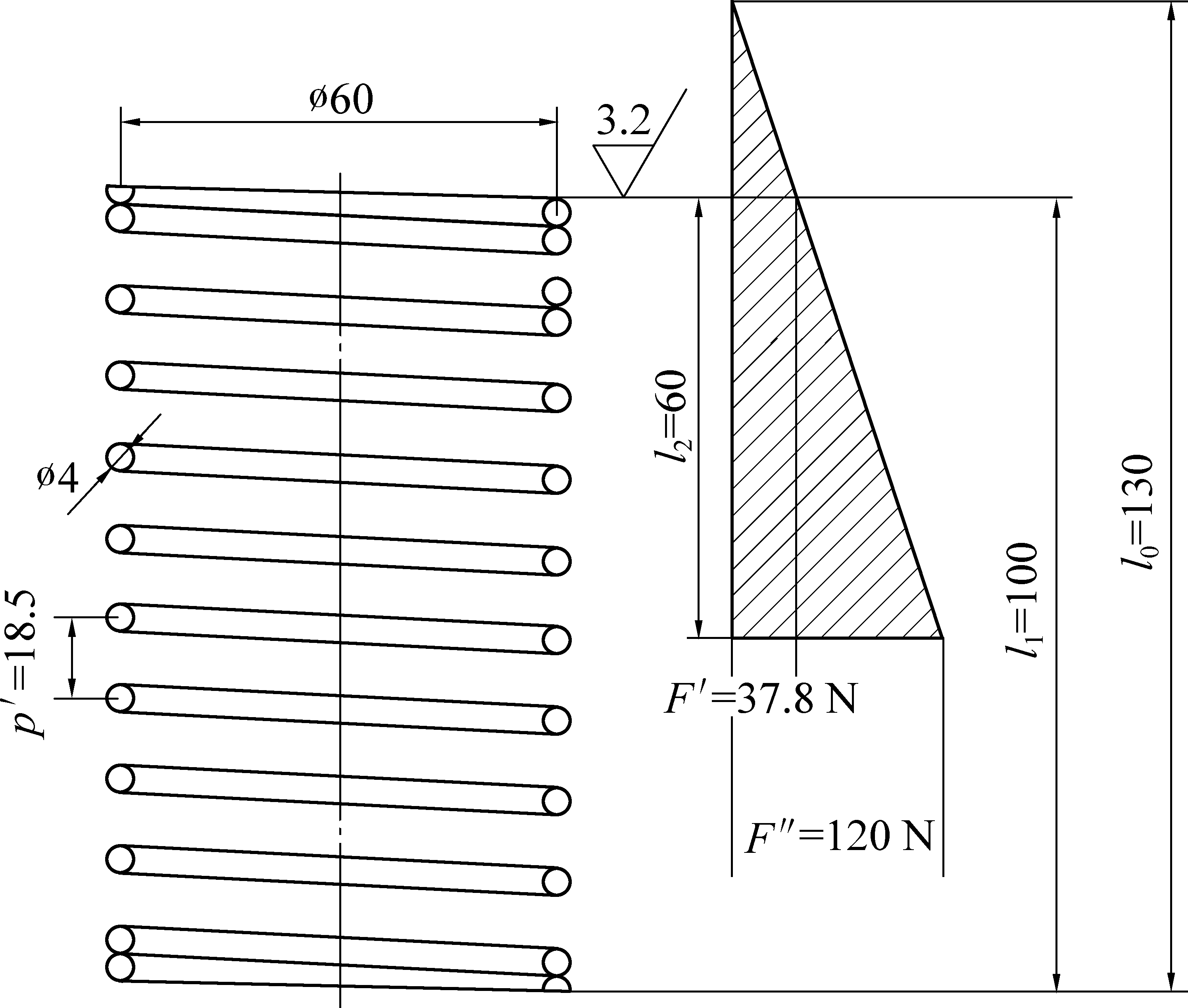
图10 复位弹簧工作原理
Fig.10 Working principle of reset spring
相关技术参数如下: 弹簧有效圈数n=9,螺旋升角αl为5.61°,展开长度L0为2 083.4 mm;弹簧端部形式为YJ型,两端并紧,每端面磨平3/4圈;热处理后硬度45-50HRC。
5 现场试验及效果分析
按照上述要求设计制造的ø300/153 mm连杆式回拉扩孔钻头如图11所示,该钻头在神华保德煤矿81309工作面进行了试用。试验工作面属8号煤层,位于山西组底部S3砂岩之上,煤层厚度在2.15~10.50 m,平均厚度7.36 m;纯煤层厚度3.19~8.84 m,平均6.01 m;为中厚-特厚煤层,以厚煤层为主。煤层结构较复杂,含夹矸0~8层,一般3~4层,夹矸总厚度0.3~2.6 m,平均厚度1.06 m。81309工作面钻孔布置如图12所示。

图11 加工完成的回拉扩孔钻头
Fig.11 Finished back reamer bit
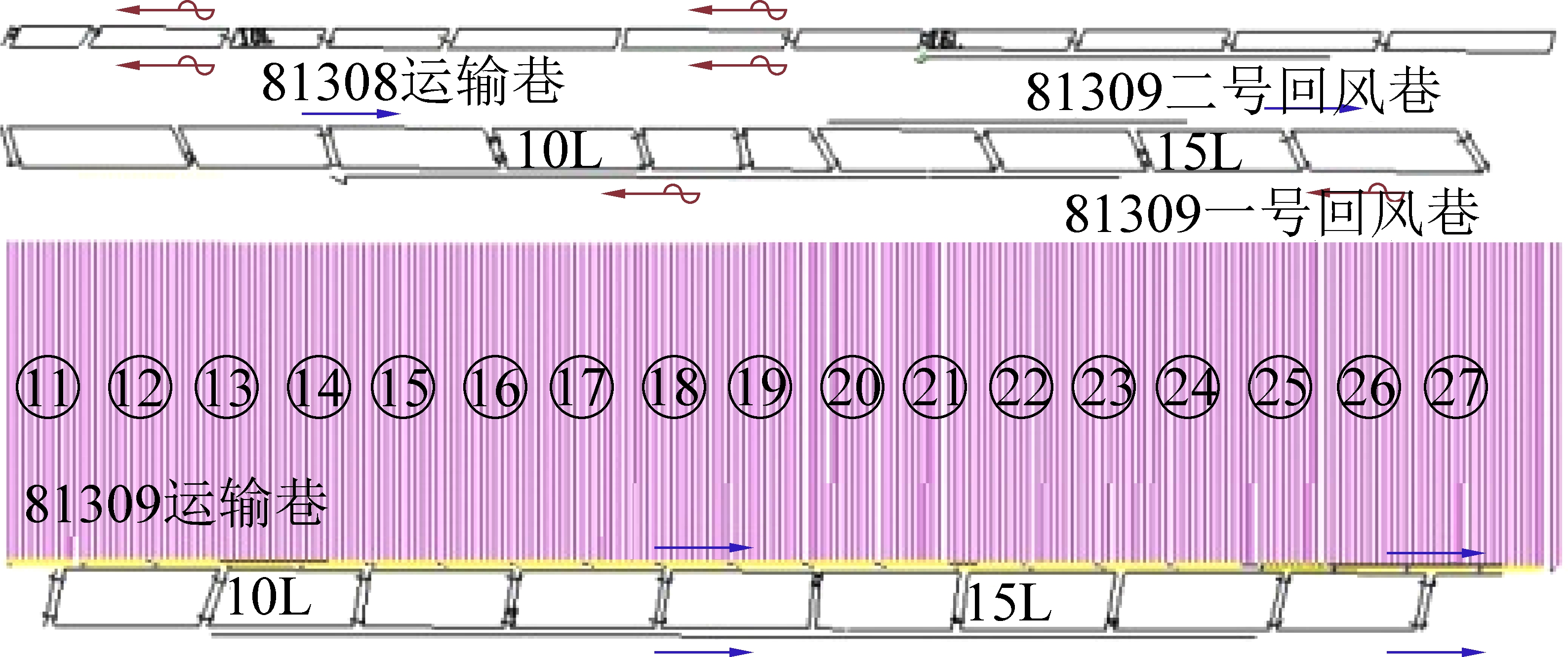
图12 81309工作面钻孔布置
Fig.12 Borehole layout of 81309 working face
试验钻具组合为:采用ø98 mmPDC钻头+0.5 m×ø73 mm扶正器+ø73 mm摩擦焊钻杆的钻具组合开先导孔,再采用ø153 mmPDC钻头+1.5 m×ø151 mm扶正器+ø73 mm摩擦焊钻杆的钻具。
工艺试验按照以下操作规程:①在回拉扩孔钻头前连接ø153 mm内凹钻头,并针对现场水压流量情况在孔口试验钻头开合情况,确定开启时流量;②进行正向钻孔施工,施工一定深度后缓慢旋转钻头,并增大水流量,待扭矩增大及返渣量增大后,提升钻具,进行回拉扩孔钻进;③完成ø300 mm回拉扩孔成孔。
试验共施工钻孔4个,累计进尺336 m,其中5-13号钻孔回拉扩孔施工16 m,5-15号钻孔回拉扩孔施工20 m,5-14号钻孔回拉扩孔施工150 m,5-16号钻孔回拉扩孔施工150 m。钻进过程中切削刀翼开合灵活,钻头钻进稳定,能够实现正常钻进保持ø153 mm钻孔钻井,回拉扩孔时实现ø300 mm钻孔回扩。钻进336 m后钻头连接部件可靠,满足了回拉扩孔钻进工艺的要求。
6 结 论
1)ø300/153 mm连杆式回拉扩孔钻头张开机构采用曲柄连杆结构,切削刀翼在张开过程中,受到的推动力矩呈现先增大后减小的趋势,推动力矩最小值出现在刀翼的初始位置;通过计算优选的弹簧既不影响钻头切削刀翼的张开过程,也能迫使切削刀翼快速可靠复位。
2)现场试验证明,ø300/153 mm连杆式回拉扩孔钻头能够实现正常钻进保持ø153 mm钻孔钻进,回拉扩孔时实现ø300 mm钻孔回扩。钻进过程中切削刀翼开合灵活,钻头钻进稳定,验证了连杆式回拉扩孔钻头结构设计及适用于普通非联络巷大直径钻孔成孔施工工艺的可行性。
3)ø300/153 mm回拉扩孔工艺能够实现提钻同时进行扩孔施工,改善了现有多级扩孔起下钻次数多、辅助时间长等问题,为煤矿井下大直径钻孔施工提供了新的方案。
[1] 雷才国,孙炳兴.大直径钻孔防治煤与瓦斯突出的实践[J].矿业安全与环保,2010,37(5):62-64.
LEI Caiguo,SUN Bingxing.Practice of large diameter drilling to prevent coal and gas outburst[J].Mining Safety & Environmental Protection,2010,37(5):62-64.
[2] 王 睿,牛国庆.大直径钻孔在瓦斯抽采中的应用[J].中州煤炭,2016(9):20-23,27.
Wang Rui,Niu Guoqing.Application of large diameter borehole in gas extraction [J].Zhongzhou Coal,2016 (9):20-23,27.
[3] 石智军,许 超,李泉新,等.煤矿井下2 570 m顺煤层超深定向孔高效成孔关键技术[J].煤炭科学技术,2020,48(1):196-201.
SHI Zhijun,XU Chao,LIQuanxin,et al.Key technology of high efficeiency hole formation for ultra deep directional hole with long 2 570 m along seam in underground coal mine[J].Coal Science and Technology,2020,48(1):196-201.
[4] 马斌文,邓志刚,赵善坤,等.钻孔卸压防治冲击地压机理及影响因素分析[J].煤炭科学技术,2020,48(5):35-40.
MA Binwen,DENG Zhigang,ZHAO Shankun,et al.Analysis on mechanism and influencing factors of drilling pressure relief to prevent rock burst[J].Coal Science and Technology,2020,48(5):35-40.
[5] 李忠辉,王恩元,郑安琪,等.煤层瓦斯抽采钻孔变形破坏测试技术及其应用研究[J].煤炭科学技术,2020,48(10):37-44.
LI Zhonghui,WANG Enyuan,ZHENG Anqi,et al.Research on testing technology of deformation and failure of boreholes in coal seam gas drainage and its application[J].Coal Science and Technology,2020,48(10):37-44.
[6] 童 碧,许 超,刘 飞,等.淮南矿区瓦斯抽采中以孔代巷技术研究与工程实践[J].煤炭科学技术,2018,46(4):33-39.
TONG Bi,XU Chao,LIU Fei,et al.Technical research and engineering practice of Kongdai Lane in gas drainage in Huainan Mining Area[J].Coal Science and Technology,2018,46(4):33-39.
[7] 赵建国.煤层顶板高位定向钻孔施工技术与发展趋势[J].煤炭科学技术,2017,45(6):137-141,195.
ZHAO Jianguo. Construction technology and development trend of high directional drilling in coal seam roof [J]. Coal Science and Technology, 2017,45(6):137-141,195.
[8] 王 鲜,许 超,王四一,等.本煤层ø650 mm大直径钻孔技术与装备[J].金属矿山,2017(8):157-160.
WANG Xian,XU Chao, WANG Siyi,et al. Large diameter drilling technology and equipment for 650mm coal seam [J]. Metal Mine, 2017(8):157-160.
[9] 司瑞江.复杂地层大直径高位定向钻孔代替高抽巷瓦斯抽采可行性及效果分析[J].能源与环保,2019,41(8):5-10,14.
SI Ruijiang. Feasibility and effect analysis of large diameter and high position directional drilling in complex stratum replacing gas extraction in high drainage roadway [J]. Energy and Environmental Protection, 2019,41(8): 5-10,14.
[10] 张 朋,高晓亮,张献振.随钻掏穴增透技术在瓦斯抽采穿层钻孔中的应用[J].煤矿机械,2019,40(9):148-150.
ZHANG Peng, GAO Xiaoliang, Zhang Xianzhen. Application of hole penetration enhancement while drilling technology in gas drainage through-layer drilling [J]. Coal Mine Machinery, 2019,40 (9): 148-150.
[11] 邬喜仓,张 迪.采动瓦斯大直径煤层钻孔埋管抽采技术及应用[J].中国煤炭工业,2017(11):60-63.
WU Xicang, ZHANG Di. Technology and application of borehole and buried pipe extraction in large diameter coal seam for mining gas [J]. China Coal Industry, 2017 (11): 60-63.
[12] 田宏杰, 王传留, 孙荣军. 煤矿井下大直径回风巷联络钻孔成孔工艺研究[J]. 中国煤炭, 2017, 43(10): 72-75.
TIAN Hongjie, WANG Chuanliu,SUN Rongjun. Study on borehole forming technology of large diameter return air tunnel in coal mine [J]. China Coal, 2017, 43 (10): 72-75.
[13] 濮良贵,纪名刚.机械设计[M].北京:高等教育出版社,2001.
[14] 路前海,王传留,高晓亮.ø300/108 mm机械式掏穴钻头的研制[J].煤炭技术,2017,36(4):263-264.
LU Qianhai, WANG Chuanliu, GAO Xiaoliang. Development of a 300/108 mm mechanical hole-digging bit [J]. Coal Technology, 2017,36(4):263-264.
[15] 于 萍. 工程流体力学[M].北京:科学出版社,2008.
[16] 韩亚东.流体力学在引射器中的应用[J].科技风,2017(2):74.
HAN Yadong. Application of fluid dynamics in ejectors [J].Science and Technology Wind, 2017 (2):74.
[17] 吴明眼.伯努利方程原理及其应用[J].信息记录材料,2018,19(9):115-117.
WU Mingyuan.Principle and application of bernoulli equation[J].Information Recording Materials, 2018,19(9):115-117.
[18] 赵昌友.伯努利方程及其应用[J].池州学院学报,2014,28(6):48-49.
ZHAO Changyou. Bernoulli equation and its application [J]. Journal of Chizhou University, 2014,28(6):48-49.
[19] 朱 卓,王晓川.流体力学在工程中的应用[J].现代冶金,2016,44(6):61-62.
ZHU Zhuo, WANG Xiaochuan. Application of fluid dynamics in engineering [J]. Modern Metallurgy, 2016,44(6):61-62.
[20] 朱绪力,滕桂荣,陈庆光,等.伯努利定理适用条件分析[J].力学与实践,2014,36(1):92-94.
ZHU Xuli, TENG Guirong, CHEN Qingguang,et al.Bernoulli theorem applicable conditions analysis [J].Mechanics and Practice, 2014, 36(1):92-94.
