0 引 言
裂纹断裂准则的研究主要致力于解决裂纹断裂的强度大小和扩展方向2 个问题[1]。 为预测裂纹的起裂和扩展,国内外学者从应力、应变和应变能角度建立了不同的断裂准则,常用的断裂推测主要有以下3 种:ERDOGAN 等[2]提出的最大周向应力准则(MTS 准则),SIH 等[3]提出的最小应变能密度因子准则(S 准则)和PALANISWAMY 等[4]提出的最大能量释放率理论(G 准则)。 但这些准则的分析结果与试验数据之间还存在一定差别,并没有准确地描述岩石的断裂机理,如MTS 准则与材料泊松比无关,不能区分平面应力和平面应变的差异,尚未被普遍接受。 断裂力学领域相关学者从不同的机理出发对断裂判别准则做了大量研究工作,文献[5-6]推导出了裂纹尖端塑性区半径,建立了R 准则,指出裂纹将会沿着裂纹尖端到弹塑性边界的最短路径扩展;任利等[7]基于Mises 屈服准则,充分考虑裂尖应力状态对于裂纹扩展区半径的影响,建立了新的断裂准则;董晗等[8]发现岩石穿透斜裂纹在单轴压缩条件下,大角度裂纹运用MTS 准则求得的理论起裂角与实际较为吻合,小角度裂纹运用摩尔库伦准则得到的理论起裂角与实际较为吻合;蒋玉川等[9]从裂纹尖端的最小无量纲塑性区尺度和广义合成偏应力强度理论相角度建立了断裂准则。 上述研究大都从应力机理出发建立的裂纹断裂判别准则,而忽略了应变这一材料断裂的判别条件。 此外,最新研究表明,岩石的断裂受裂纹尖端奇异项应力强度因子及常数项T 应力的共同控制[10-12]。 且越来越多的试验证明,不考虑T 应力的断裂准则预测结果存在较大误差[13-15]。 建立裂纹扩展的临界条件是断裂力学研究中的重要任务,然而无论何种断裂准则都与裂纹尖端应力-应变场的分布特征有关。 笔者主要以裂纹尖端应力场的WILLIAMS 级数解和胡克定律为基础,建立了考虑T 应力影响的最大周向拉应变准则,在裂纹尖端应变场分析的基础上,对裂纹扩展规律与岩石材料性质和T 应力的关系进行了研究。
1 裂纹尖端应力场级数解
传统的强度理论假设材料为连续介质,显然不适用于含裂纹结构。 WILLIAMS 建立了以裂纹尖端顶端为原点的极坐标下裂纹尖端应力场(图1)的幂级数展开式,取应力级数解的前2 项,可表示为
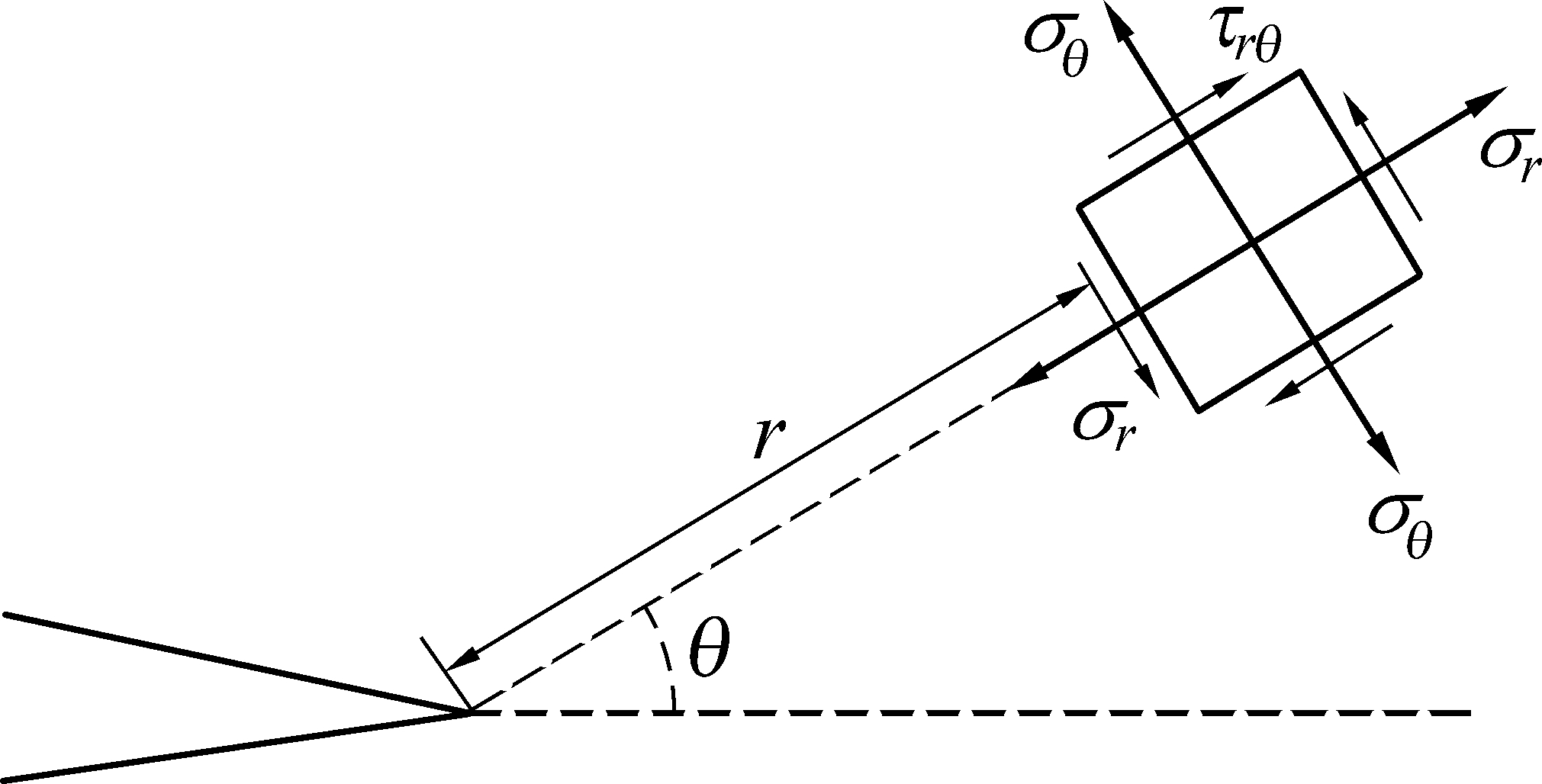
图1 裂纹尖端应力场变量
Fig 1 Stress field variables at crack tip
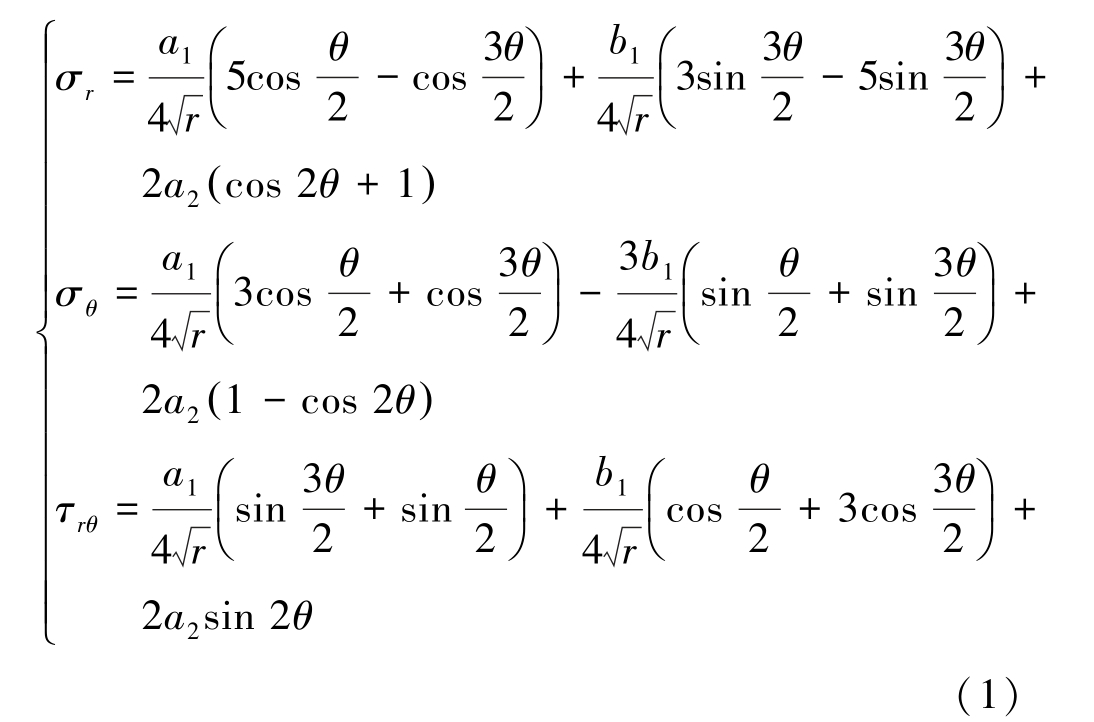
将式(1)改为以应力强度因子和T 应力表示的常见形式为
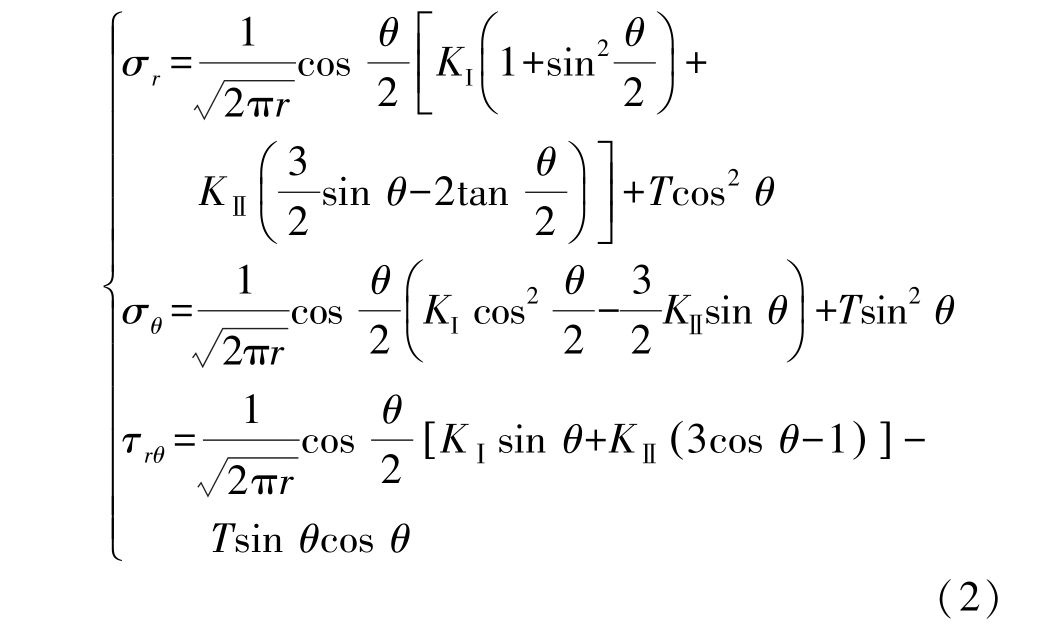
根据胡克定律可知,在极坐标下裂纹尖端各应变分量可表示为

式中: σr、σθ、τrθ 分别为裂纹尖端径向应力、周向应力和剪应力,MPa;a1、b1为无量纲系数;r 为裂纹尖端半径,mm;θ 为裂纹尖端夹角,(°);εr、εθ、γrθ 分别为裂纹尖端径向应变、周向应变和剪切应变;KⅠ,KⅡ分别为Ⅰ型和Ⅱ型断裂韧性,即临界应力强度因子,MPa·![]() ;T 为平行于裂纹方面的应力分量,即T 应力,MPa;E 为材料弹性模量,MPa;μ 为泊松比。
;T 为平行于裂纹方面的应力分量,即T 应力,MPa;E 为材料弹性模量,MPa;μ 为泊松比。
2 最大周向应变裂纹扩展准则
对于线弹性材料,最大周向应变理论认为:①裂纹起裂发生在裂纹尖端径向沿周向应变εθ 最大的方向上;②根据周向应变εθ取得极大值εθmax的条件确定裂纹扩展方向θ0;③断裂发生在沿裂纹尖端径向距离rc 处且周向应变εθ超过临界值εc。 上述条件中,rc和εc是材料的固有属性。 根据上述条件,最大周向裂纹扩展应变准则的数学表达式为
以无限大平板内含长度为2d 的裂纹为研究对象,平板纵向分布均匀载荷σ,横向载荷为kσ,k 为横向载荷系数,裂纹倾角为β,如图2 所示。 在该模型中应力强度因子及T 应力表达式为
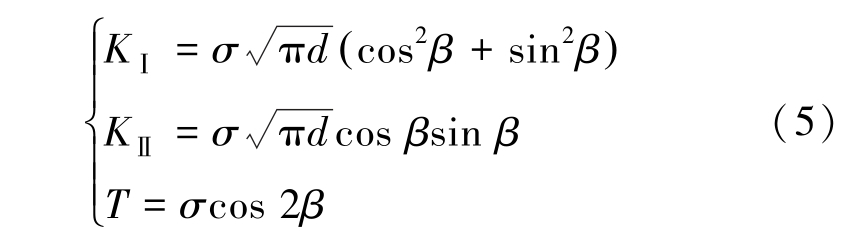
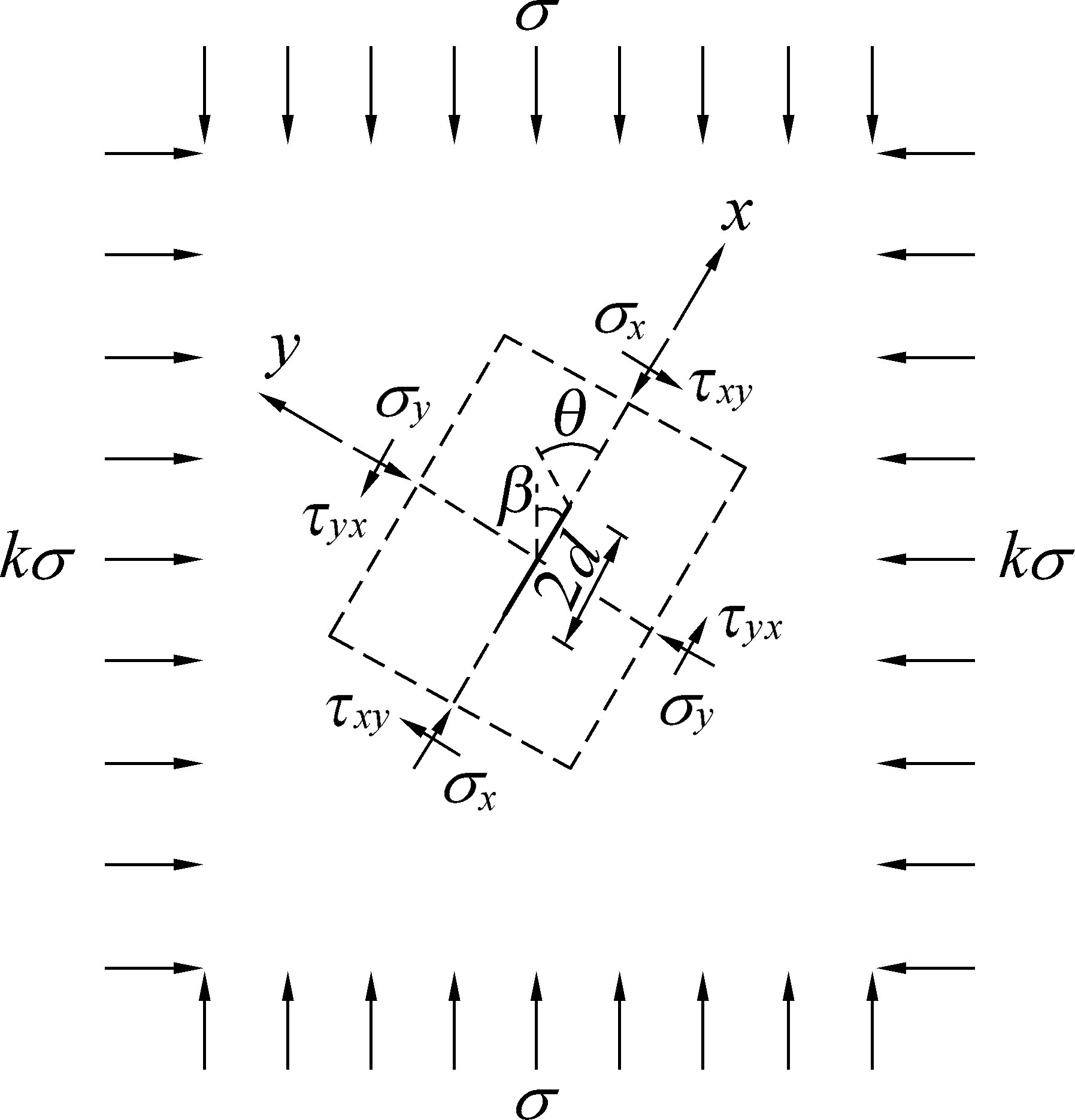
图2 无限大平板内含倾斜直裂纹
Fig.2 An angled crack in a biaxial compressive infinite plate
σx、τxy—沿x 方向的正应力、剪应力;σy、 τyx—沿y 方向的正应力、剪应力
为方便下文讨论,引入无量纲特征距离α 为
将式(3)、式(5)和式(6)代入式(4)可得裂纹起裂判别依据:
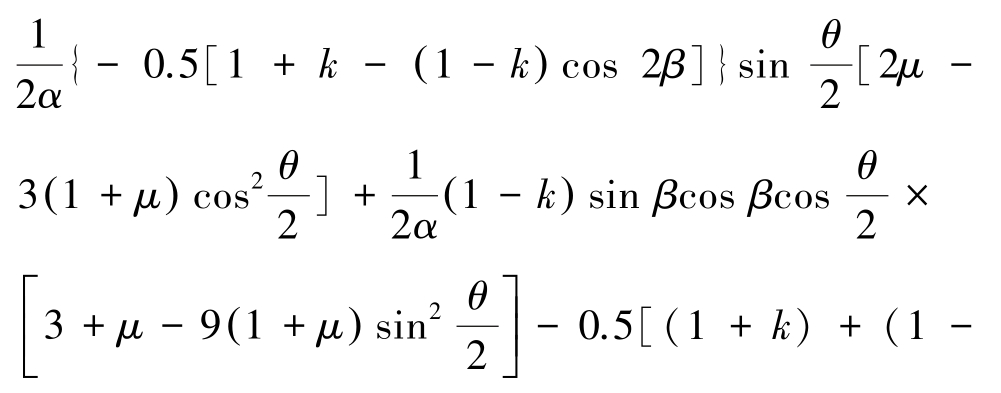
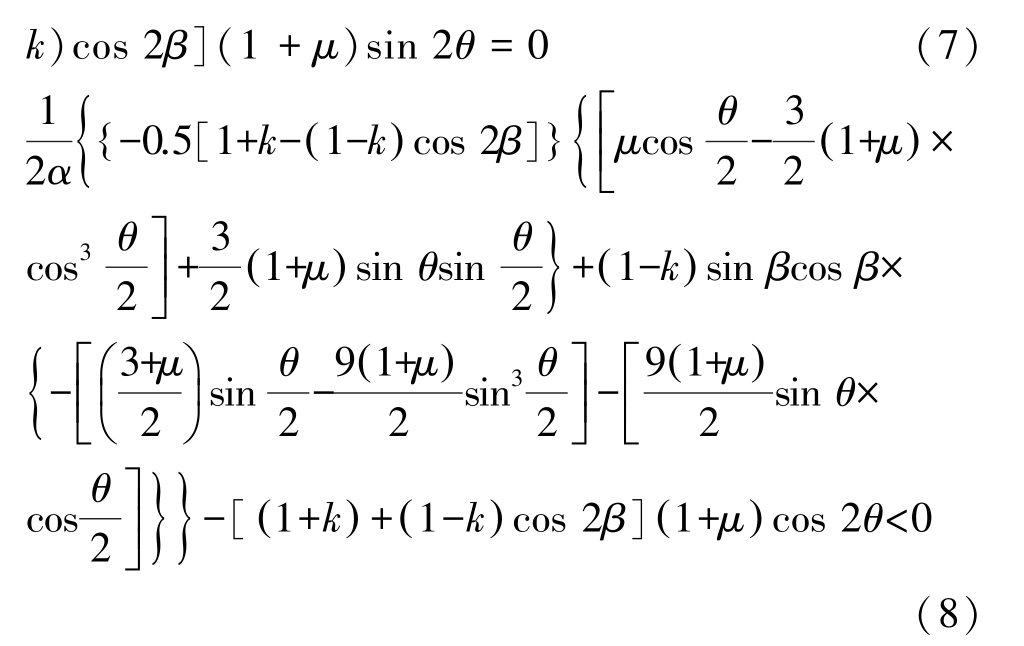
根据式(7)和式(8)即可得到泊松比、无量纲特征距离、裂纹倾角及围压系数等因素对脆性材料断裂行为的影响。
3 最大周向应变裂纹扩展准则解析
3.1 裂纹尖端应变场
以无限大平板内含裂纹模型为例,取纵向载荷σ =10 MPa,横向载荷系数k =0,弹性模量E =20 GPa,泊松比μ=0.2,并假设无量纲特征距离α=0.5,将上述参数代入式(3)中,可得考虑T 应力的裂纹尖端周向应变分布,计算得到裂纹倾角分别为15°和60°时,裂纹尖端夹角-90°~90°内周向应变曲线,将不考虑T 应力的周向应变值列于图中进行对比,结果如图3 和图4 所示。
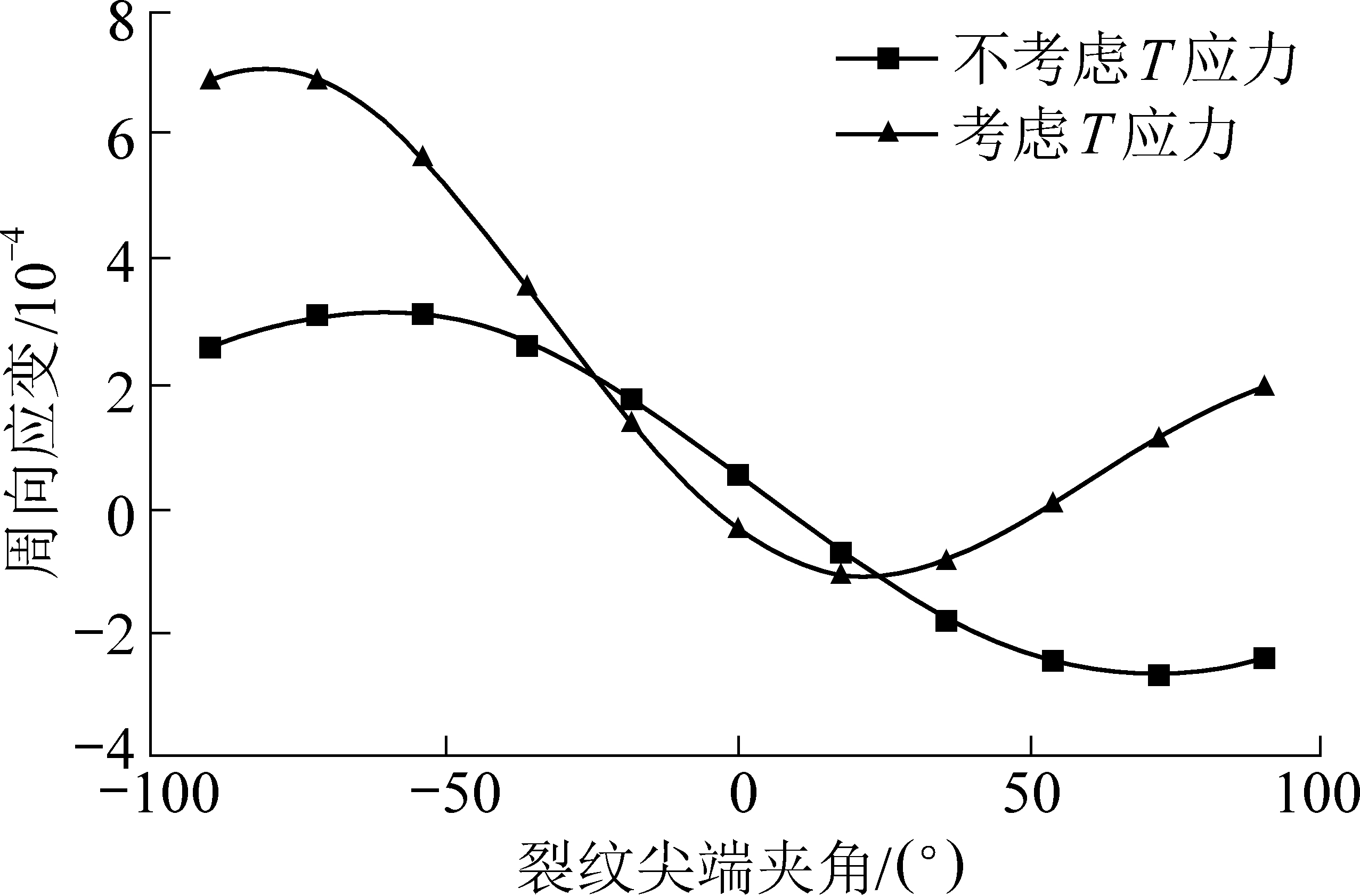
图3 裂纹倾角为15°时尖端周向应变分布
Fig.3 Crack tip circumferential strain distribution when crack dipping angle is 15°
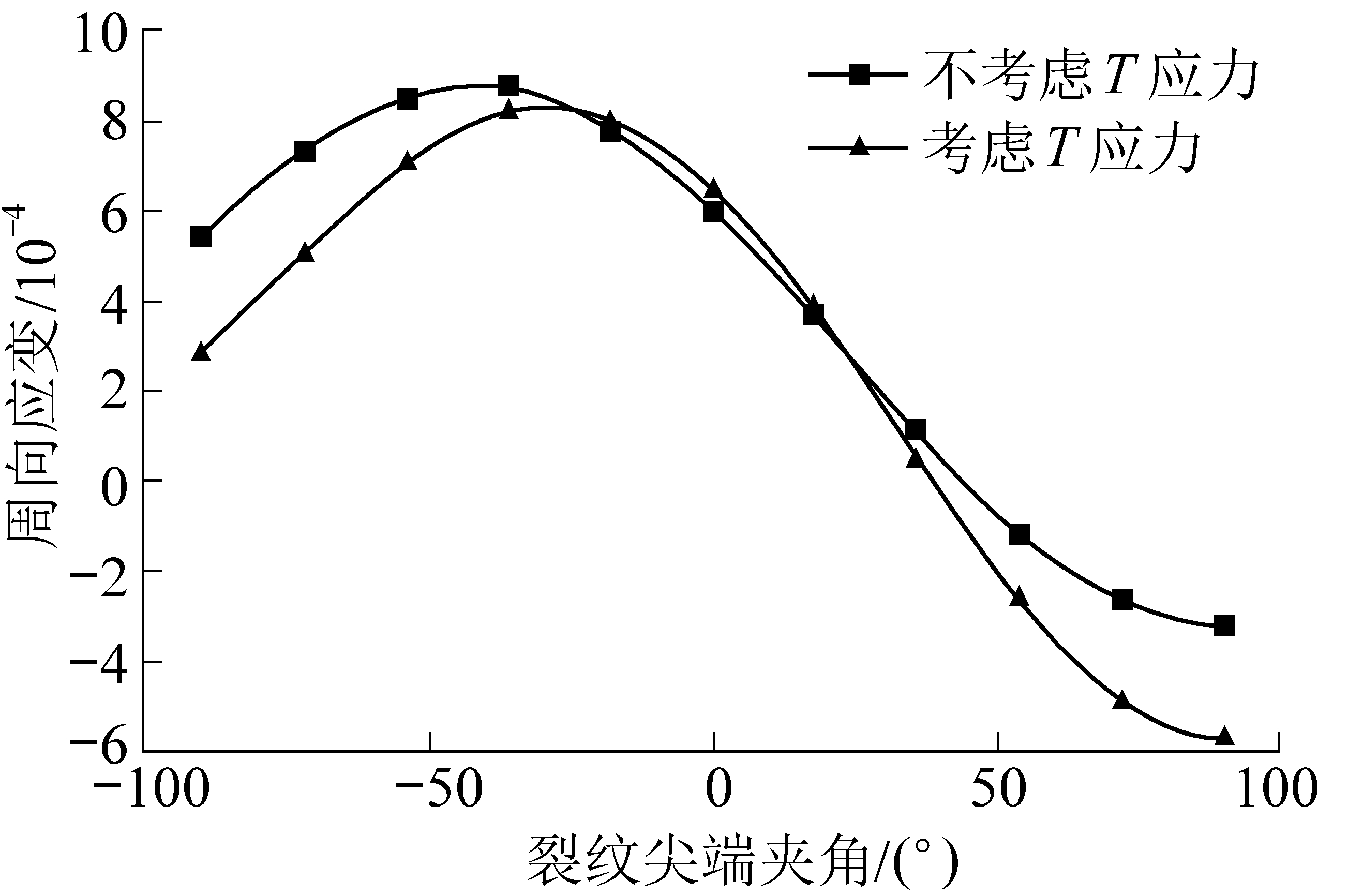
图4 裂纹倾角为60°时尖端周向应变分布
Fig.4 Crack tip circumferential strain distribution when crack dipping angle is 60°
由图3 和图4 可知,考虑T 应力后,裂纹尖端周向应变分布产生显著变化,且周向应变取得极值的裂尖角度,即裂纹初始起裂角同样发生改变,若忽略T 应力,会得出错误的裂纹尖端应变场分布特征,进而得到带有很大误差的裂纹初始起裂角。
3.2 T 应力对裂纹起裂角的影响
将3.1 节无限大平板内含裂纹模型参数代入式(3)中,可得不同裂纹倾角情况下,沿裂纹尖端旋转1 周的周向应变曲线,计算结果如图5 所示。
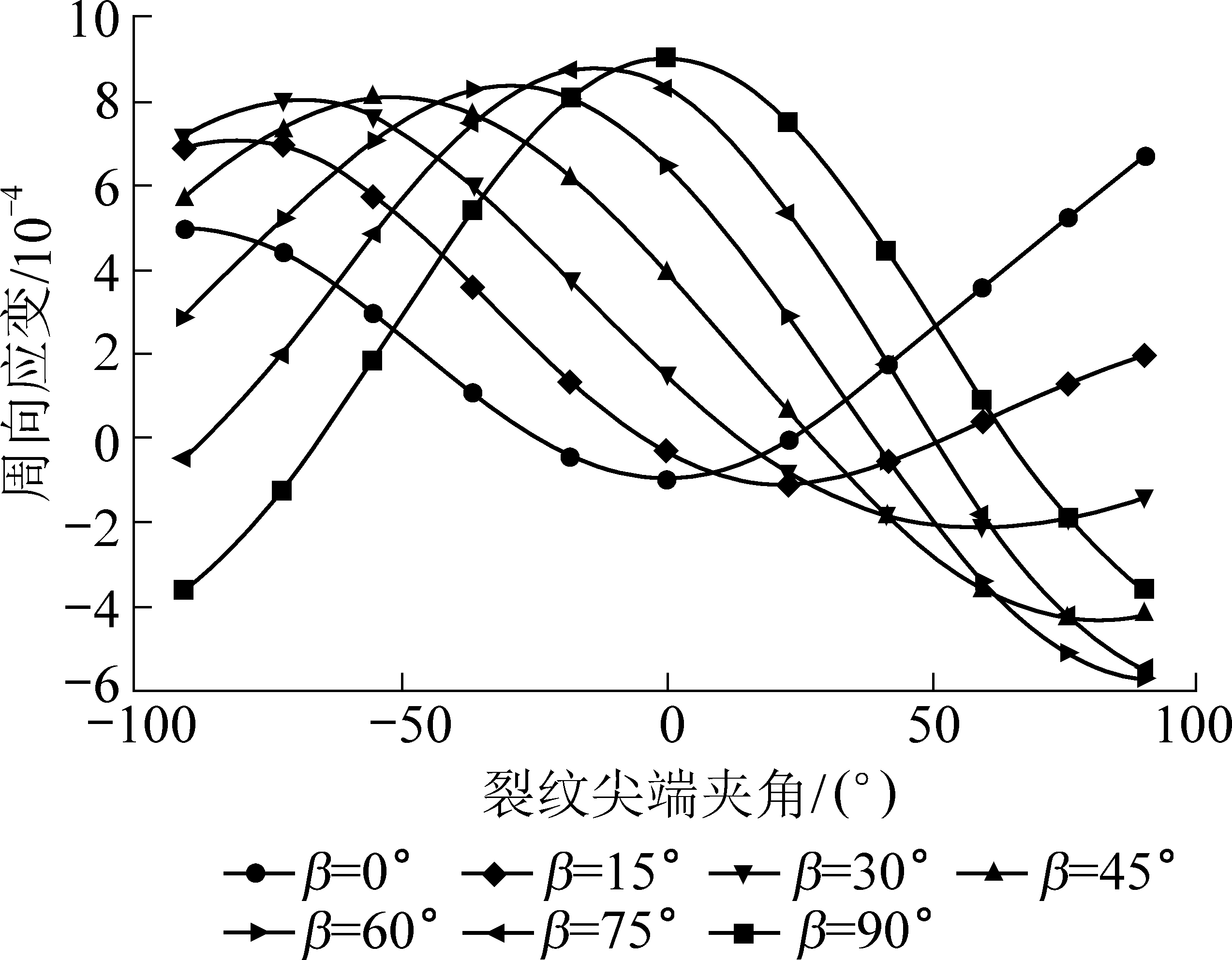
图5 不同裂纹倾角下裂纹尖端周向应变分布
Fig.5 Circumferential strain distribution at crack tip with different dip angles
提取不同裂纹倾角下的裂纹尖端周向应变最大值对应的角度,即为不同裂纹倾角时材料的初始起裂角,进而可以得到最大周向应变准则预测的裂纹起裂角随裂纹倾角的变化规律,如图6 所示。 由图6 可知,裂纹起裂角均随着裂纹倾角的增大而减小,当裂纹倾角为0 时,不考虑T 应力的最大周向应变准则预测的裂纹起裂角为66°,而考虑T 应力的预测结果为90°;当0°<β<45°时,若不考虑T 应力,预测结果偏小,当45°<β<90°时,预测结果偏大。
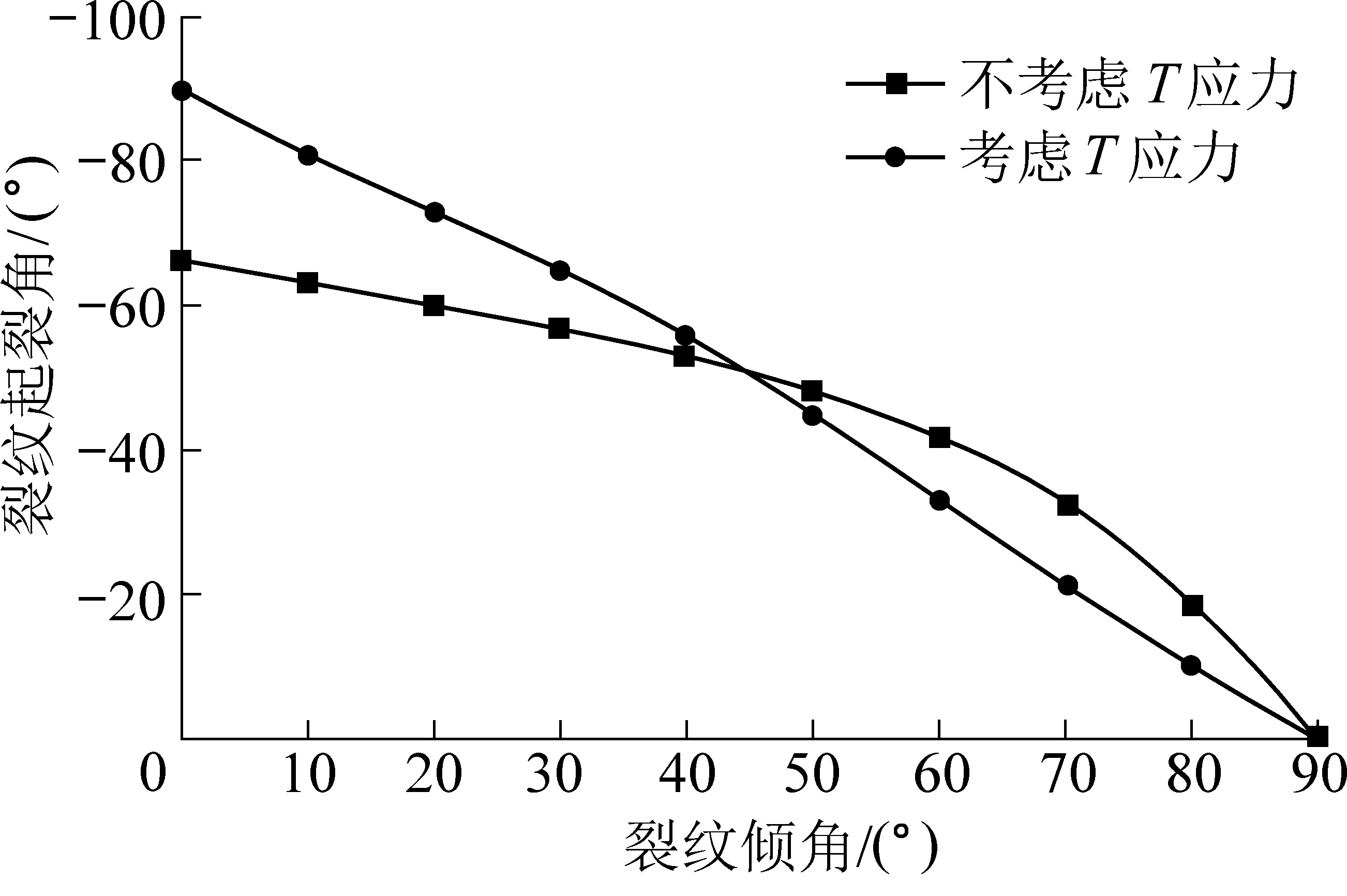
图6 裂纹起裂角与裂纹倾角的关系曲线
Fig.6 Relation curves between critical angle and crack orientation angle
3.3 无量纲特征距离对裂纹起裂角的影响
同样,假设μ=0.2,可得不同无量纲下的裂纹起裂角随裂纹倾角的变化规律,如图7 所示。 当裂纹倾角为0°时,不同无量纲条件下,考虑T 应力的最大周向应变准则预测的裂纹起裂角均为-90°;当0°<β<45°时,裂纹起裂角预测结果随α 的增大而增大,且对裂纹倾角的变化更加敏感;当45°<β<90°时,裂纹起裂角预测结果随α 的增大而减小,但随裂纹倾角的增大,裂纹起裂角的变化幅度逐渐减小。
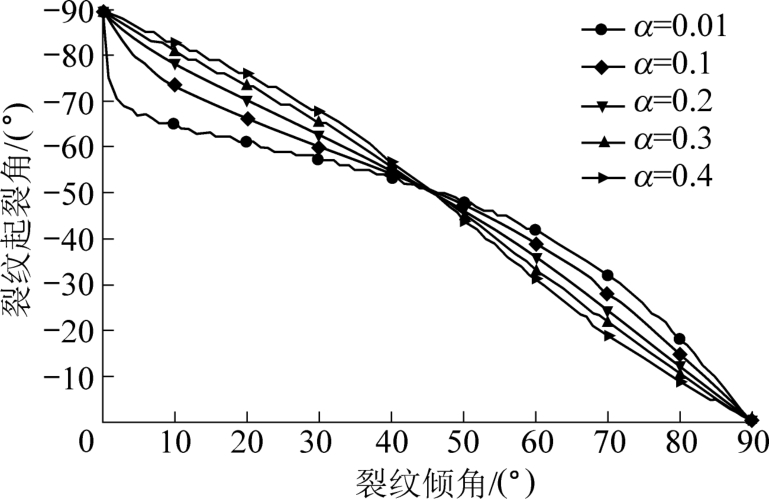
图7 无量纲特征距离对裂纹起裂角的影响
Fig.7 Effect of dimensionless feature distance on crack initiation angle
4 最大周向应变裂纹扩展准则验证
T 应力和α 对裂纹起裂角有重要影响,采用考虑T 应力的最大周向应变准则判断岩石裂纹的断裂特征能够弥补基于应力的裂纹扩展判别准则的不足。 为验证最大周向应变准则的有效性,将不考虑T 应力的最大周向应变准则的起裂角预测值、不同α 时的预测值及WILLIAMS 和EWING[18]不同裂纹倾角的裂纹起裂角试验结果进行对比(图8)。
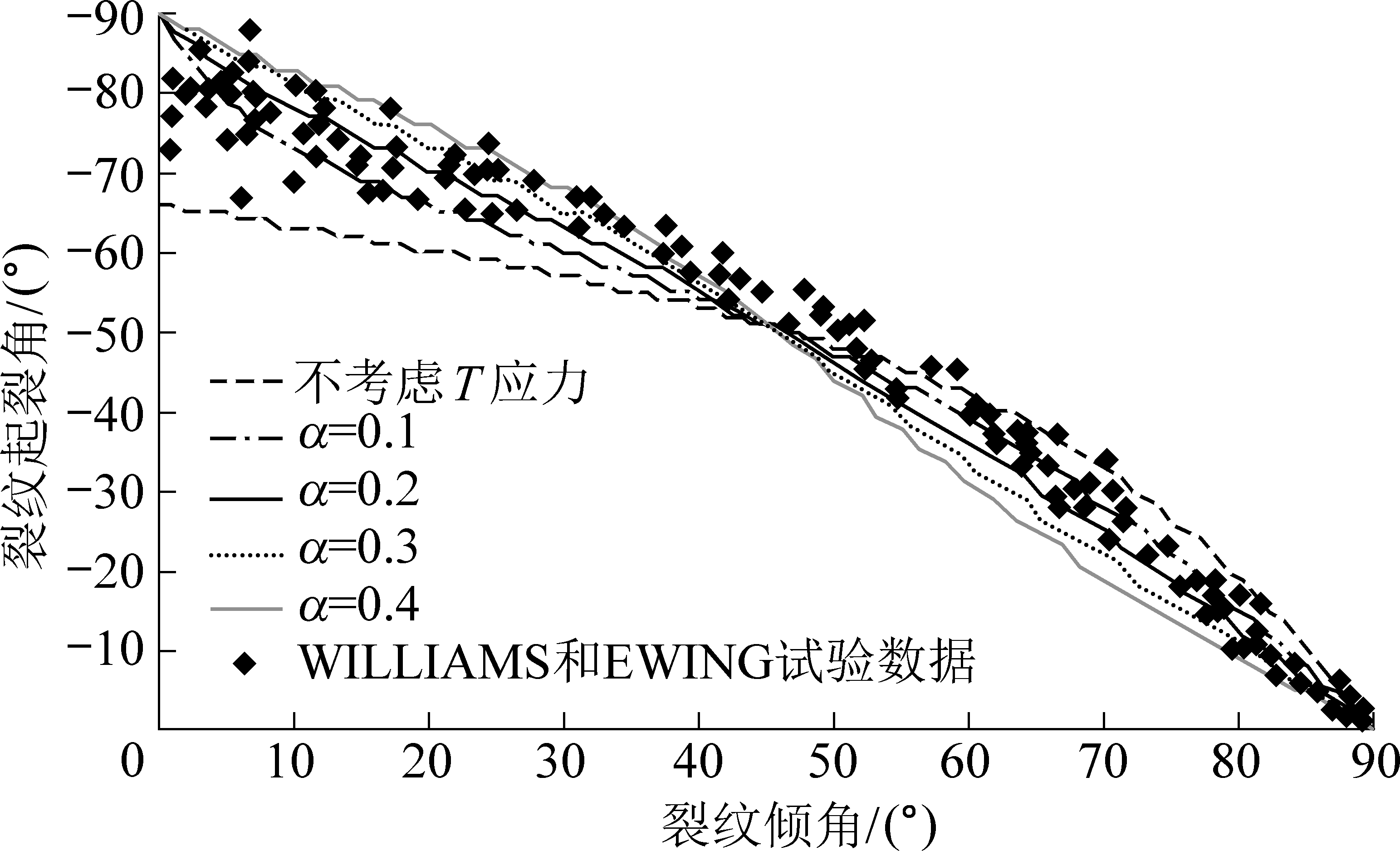
图8 岩石裂纹起裂角随裂纹倾角的变化曲线
Fig.8 Curve of initiation angle and crack orientation angle
聚甲基丙烯酸甲酯材料(PMMA)具有良好的均质性和硬脆性,可排除材料性质对试验结果的影响。WILLIAMS 和EWING 将该材料制成含倾斜裂纹的平板,开展了不同裂纹倾角的拉伸试验,所用设备为WE300 型万能试验机试验过程采用位移控制,加载速率为0.01 mm/min,保证裂纹的扩展始终处于准静态状态,得到不同裂纹倾角平板的初始起裂角的试验数据如图8 所示。 由图8 可知,考虑T 应力修正之后的最大周向应变准则预测值与试验数据更加吻合,且预测结果基本分布在无量纲参数为0.1 ~0.2。 若不考虑T 应力的影响,理论预测值与试验结果存在很大误差,当β<45°时,预测值偏小,当β>45°时,预测值偏大,且裂纹倾角越小,误差越大;当裂纹倾角较大时,Ⅰ型断裂占主导地位,此时T 应力较小,裂纹扩展主要受奇异项应力强度因子控制,因此,不考虑T 应力的预测值与试验结果误差较小,而当裂纹倾角较小时,Ⅱ型断裂占主导地位,T 应力偏大,裂纹扩展受T 应力和应力强度因子的共同作用,T 应力的影响不可忽略,因此误差偏大。
5 结 论
1)当裂纹倾角为0 时,不考虑T 应力的最大周向应变准则预测裂纹起裂角为66°,而考虑T 应力后预测结果为90°;当45°<β<90°时,裂纹起裂角预测结果随α 的增大而减小;当0°<β<45°时,裂纹起裂角预测结果随α 的增大而增大,且对裂纹倾角的变化更加敏感。
2)不考虑T 应力的最大周向应变准则预测值存在很大误差,且在II 型断裂占主导地位时,误差更大;考虑T 应力后,预测值与试验数据更加吻合;T 应力的加入使裂纹尖端应力场解析式对裂纹尖端应力分布的描述更加精确,因而提高了对裂纹扩展特征预测精度;脆性材料裂纹扩展受到裂纹尖端应力强度因子及常数项T 应力的共同控制。
3)考虑T 应力的最大周向应变准则描述了I 型和II 型断裂应力强度因子、断裂韧性KⅠ和KⅡ、T 应力以及临界裂纹扩展区半径和泊松比对裂纹扩展的影响,弥补了基于应力的裂纹扩展判别准则的不足,研究结果可为水力压裂、煤层开采等岩土工程中的裂纹扩展问题提供理论支撑和指导。
[1] 郦正能, 张纪奎. 工程断裂力学[M]. 北京:北京航空航天大学出版社, 2012.
[2] ERDOGAN F, SIH G C. On the crack extension in plates under plane loading and transverse shear[J]. Journal of Basic Engineer⁃ing, 1963, 85(4):527.
[3] SIH G C. Strain-energy-density factor applied to mixed mode crack problems[J]. International Journal of Fracture, 1974, 10(3):305-321.
[4] PALANISWAMY K, KNAUSS W G. Propagation of a crack under general, in-plane tension[J]. International Journal of Fracture Mechanics, 1972, 8(1):114-117.
[5] KHAN S M A,KHRAISHEH M K. A new criterion for mixed mode fracture initiation based on the crack tip plastic core region[J]. In⁃ternational Journal of Plasticity, 2004, 20(1):55-84.
[6] 王 超,朱哲明,刘宏杰. 裂纹起裂角预测方法研究[J]. 四川大学学报(工程科学版), 2015, 47(2):28-35.WANG Chao, ZHU Zheming, LIU Hongjie. Study on predicting crack initiation angle[J].Journal of Sichuan University (Engineer⁃ing Science Edition), 2015,47(2):28-35.
[7] 任 利, 朱哲明, 谢凌志,等. 复合型裂纹断裂的新准则[J].固体力学学报, 2013, 34(1):31-37.REN Li, ZHU Zheming, XIE Linzhi,et al. New fracture criterion for mixed mode cracks[J].Journal of Mechanics of Solids, 2013,34(1):31-37.
[8] 董 晗. 单轴压缩下岩石斜裂纹扩展规律研究[D].重庆:重庆大学, 2016.
[9] 蒋玉川, 徐双武, 陈 辉. 脆性材料复合型裂纹的断裂准则[J]. 工程力学, 2008, 25(4):50-54.JIANG Yuchuan, XU Shuangwu, CHEN hui. The fracture criterion of the mixed-mode cracks in brittle material′s[J]. Engi⁃neering Mechanics, 2008,25(4):50-54.
[10] 赵艳华, 陈 晋, 张 华. T 应力对Ⅰ-Ⅱ复合型裂纹扩展的影响[J]. 工程力学, 2010, 27(4):5-12.ZHAO Yanhua, CHEN Jin, ZHANG Hua. Effect of T stress on crack propagation for I-II mixed mode loading[J].Engineering Mechanics,2010,27(4):5-12.
[11] 刘 津. T 应力对混凝土断裂韧度的影响[D].大连:大连理工大学, 2014.
[12] AYATOLLAHI M R,ALIHA M R M. On the use of brazilian disc specimen for calculating mixed mode I-II fracture toughness of rock materials[J]. Engineering Fracture Mechanics, 2008, 75(16):4631-4641.
[13] 周绍青, 郭少华, 李显方. T 应力对岩石断裂韧度及扩展路径的影响[J]. 中南大学学报自然科学版, 2009, 40(3):797-802. ZHOU Shaoqing, GUO Shaohua, LIXianfang. T-stress′s impact on rock′s fracture toughness and propagation path[J].Journal of Central South University (Science and Technology),2009,40(3):797-802.
[14] LARSSON S G,CARLSSON A J. Influence of non-singular stress terms and specimen geometry on small-scale yielding at crack tips in elastic-plastic materials[J]. Journal of the Mechanics &Physics of Solids, 2009, 21(21):263-277.
[15] COTTERELL B,RICE J R. Slightly curved or kinked cracks[J].International Journal of Fracture, 1980, 16(2):155-169.
[16] FLECK N A, HUTCHINSON J W,SUO Z. Crack path selection in a brittle adhesive layer[J]. International Journal of Solids &Structures, 1991, 27(91):1683-1703.
[17] TVERGAARD V, HUTCHINSON J W. Effect of, ja:math, on mode I crack growth resistance in a ductile solid[J]. International Journal of Solids & Structures, 1994, 31(6):823-833.
[18] WILLIAMS J G, EWING P D. Fracture under complex stress-The angled crackproblem[J]. International Journal of Fracture Me⁃chanics, 1984, 26(4):346-351.
