0 引 言
坑道钻探是煤炭安全高效开采地质保障的重要手段，随着近年来煤矿智能化发展，钻探技术也在不断探求精准化、智能化发展的途径［1-3］。 钻探过程中的钻柱动力学是基础理论问题，由于含煤地层的非连续性、非均质性和钻头回转切削机械破岩方式等因素，钻进过程中钻具的纵振、横振和扭振相互叠加耦合，给钻具的使用寿命和钻进精准控制带来不利影响，但同时其动力响应信号可有效表征钻探过程，与钻速、转矩、钻压、转速等常规随钻参数［4-8］共同为地层信息预测提供重要数据。 对钻进过程动力特性的深入研究对于煤矿井下坑道钻探施工中的智能探查具有重要意义［9-11］。
钻柱动力学一直是钻井工程力学的重点和难点，国内外学者结合钻井实际开展了大量卓有成效的动力特性方面的研究。 MORADI 等［12］采用金相分析和有限元计算相结合的方法对钻柱振动特性和失效特征进行了分析。 GUPTA 等［13］在考虑切削力和转矩对钻柱轴扭耦合振动影响的基础上，提出可提高钻进系统稳定性的技术条件。 刘清友等［14］基于钻井系统动力学行为理论，开展了非线性系统的数值求解方法研究。 朱才朝等［15］在考虑随机载荷作用下，建立了典型工作状态下钻柱系统耦合非线性动力学模型。 刘永升等［16］建立了斜直井中钻柱非规则运动的4 自由度非线性动态模型，进一步认识了斜井段和水平段的钻柱工况。
与钻井系统中的超大长径比的大柔性钻柱系统不同，以巷道锚固孔为代表的小口径（≤50 mm）短钻深（≤15 m）的井巷工程钻孔的动力学规律表现出自身的特点。 由于原始沉积作用和后期构造作用造成含煤地层特性差异较大，加之岩石钻进破碎过程本身的复杂非线性，导致虽然煤矿井下锚固孔施工相对快速简单，但仍无法依据成熟的力学理论准确描述钻进动力过程。 近年来一些学者采用数值模拟方法对煤矿井下PDC（Polycrystalline Diamond Compact）钻头钻进过程进行了数值模拟分析。 孟传明［17］采用弹塑性煤岩损伤模型对钻进破岩过程进行仿真，获得了钻头的阻力载荷及破岩特性等数据。张幼振等［18］应用有限元仿真对孔底煤岩应力变化和钻头动力响应特征进行了分析。 文献［19-20］基于煤巷顶板锚固孔钻进过程中钻杆振动机理，利用数值模拟方法，分析了不同强度岩石条件下的振动响应特征。 由此可知，数值模拟中约束限制条件多，对设置的边界和载荷条件敏感，通用性不强。 笔者在分析钻柱动力学理论基础上，运用解析法对动载响应条件下的钻具压入、切削和振动过程分别进行分析，建立振动数学解析模型，并以有限元仿真为计算验证手段，进一步分析了钻头载荷钻进过程中的变化规律，最后在实钻试验中完成了动力响应信号提取与识别，为深入研究煤矿井下智能钻探技术和提高钻探质量提供了理论基础与技术途径。
1 钻柱系统动力学模型
1.1 钻柱系统动载受力分析
在含煤地层锚固孔施工过程中，钻杆、钻头等组成的钻柱系统承受着自重、给进阻力、转矩、阻尼、钻杆与孔壁接触碰撞力及钻杆与煤岩摩擦阻力等综合作用，不仅会产生纵向、横向、扭转振动，还可能产生耦合振动。 为进行钻柱系统在含煤地层施工中的动载受力分析，可对相关条件进行简化和假设［21-22］：①含煤地层为弹塑性体；②钻具为绝对刚体；③钻具振动时仅考虑粘滞阻力；④钻头为两翼弧角PDC 内凹锚杆钻头，钻头端部始终保持与岩石接触；⑤钻杆与孔壁间的碰撞为弹性碰撞，钻孔轴线与钻具轴线重合。 钻柱系统动载受力分析如图1 所示。
由图1 可知，钻柱系统施工过程中，转速为n，钻速为v，由于钻柱系统承受钻机提供的给进力FT、转矩MT和自身重力Fg 近似为恒定值，所以钻柱系统受力分析主要研究地层作用的动载轴向力Fa、动载切向力Fb和转矩Md。
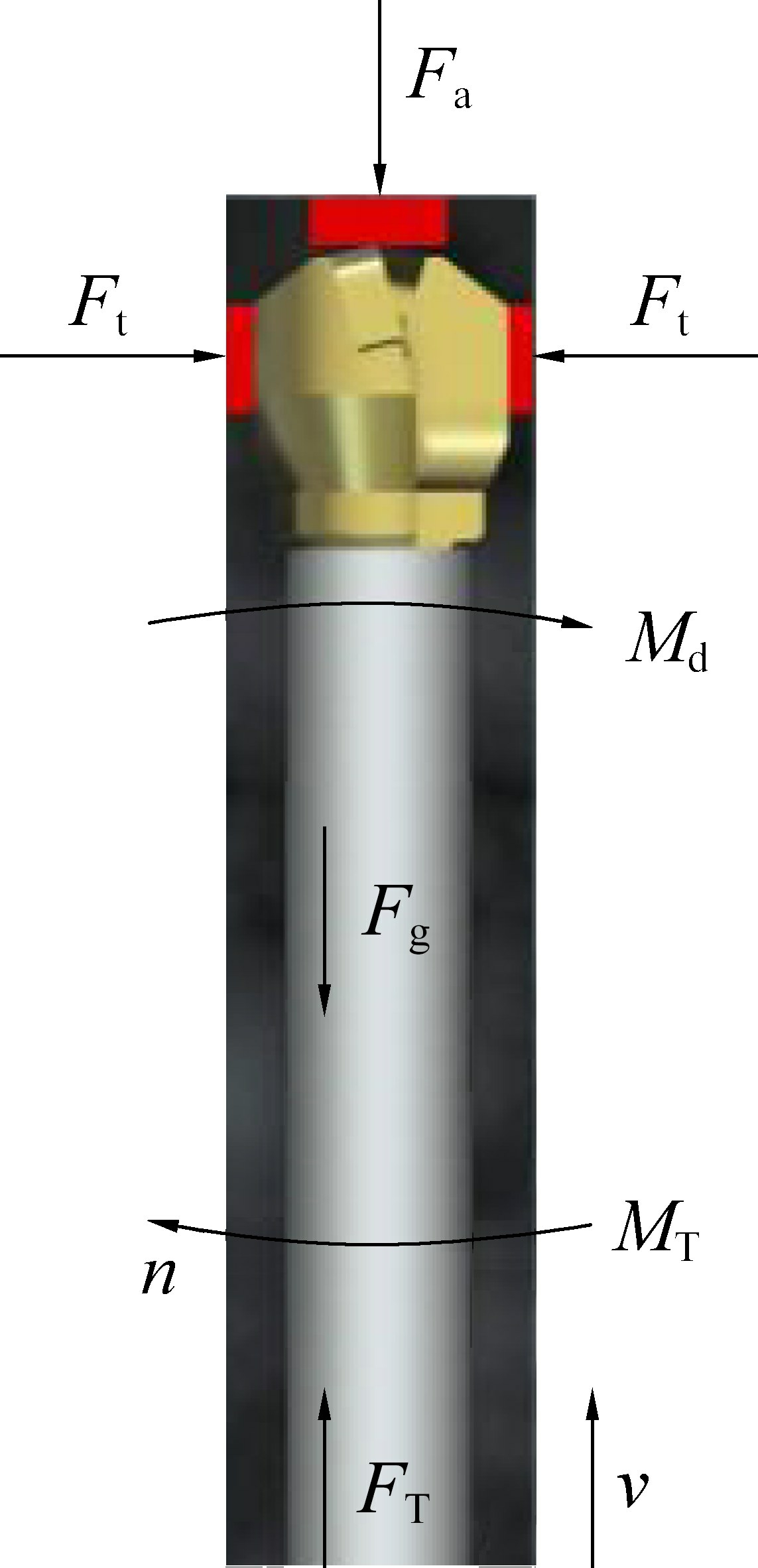
图1 钻柱系统动载受力分析示意
Fig.1 Schematicof dynamic load analysis of drill string system
1）地层作用的动载轴向力Fa 。 在静力加载下，当钻头压入含煤地层深度为d 时，根据斜镶圆柱体PDC 钻头垂直压入岩石的受力状态分析［23］，可得轴向压入面积为
式中：θ 为切削前角，（°）；R 为钻头切削齿半径，mm。
则地层在压入过程中作用在钻头上的静载轴向力Fc 为
式中，σb 为岩石抗压强度，MPa。
根据岩石波动力学，在动载条件下，考虑钻速v的影响，岩石的力学性质随应变速率的变化而变化［24］。 当应变速率小于某一临界值时，其动应力近似与钻速v 成正比，与岩石波速c 成反比，动态弹性模量与静态弹性模量变化不大，根据动应力计算方法可以得出地层作用的动载轴向力Fa 表示为
式中：E 为岩石弹性模量，MPa；c 为岩石波速，km/s；η 为压入黏度系数。
2）地层作用的动载切向力Fb。 根据传统切削力计算方法可得岩层在钻头切削面上的静切向力为
式中：σt 为切削应力，MPa； S′ 为切削面积，mm2； f为应力分布系数，与切削前角有关； τJ 为岩石抗剪强度，MPa；φ 为剪切角，（°）。
与岩石直接接触切向面是垂直面的投影面，即
由于PDC 钻头每个切削齿在单次切削过程中切除相当于1/2 的圆柱体积的岩石，该体积的截面积为顶角180°、深度H 的扇形，重心位置距顶点的距离为
，若将切削体看成整体，则其转动惯量J为
，得出其动量矩L 为
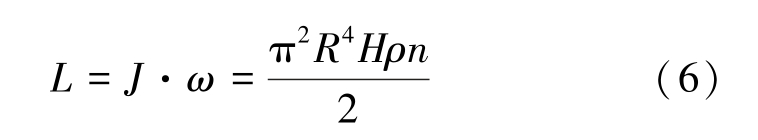
对单个切削齿的首末段应用动量矩定理，即
式中：w 为角速度，rad/s；t 为切削时间，s； ρ 为岩石密度，kg/m3；FM为动载合力；dM为合力距。
可得动载合力FM 为
即地层作用的动载切向力Fb 可表示为
3）地层作用的转矩Md。 忽略钻柱系统的弯曲变形和与孔壁的摩擦作用，可以得出地层作用的扭矩Md 为
式中：G 为钻具的剪切弹性模量，MPa；A 为钻具的截面积，m2；δ 为扭转角度，（°）；dx 为钻柱系统轴向微元端。
依据含煤地层力学测试结果［25］，以典型煤层锚固孔钻进为例进行分析，岩石抗压强度σb 为11.5 MPa，岩石抗剪强度τJ 为1.2 MPa，钻头切削齿半径R 为5.5 mm，压入黏度系数η 为0.65，切削前角θ 为15°，剪切角φ 为24°，转速n 为120 r/min。 得到的钻柱系统在煤层的动载受力情况如图2 所示。
由图2 可知，在典型煤层中，动载轴向力和切向力均随压入深度的增大而增加，幅值区间为0.18 ～0.31 kN；作用力曲线与右侧Y 轴交点为静力加载条件下的岩层作用力，动载轴向力和切向力均随钻速的增大而增加，但整体变化相对较小，幅值区间为0.17～0.29 kN。
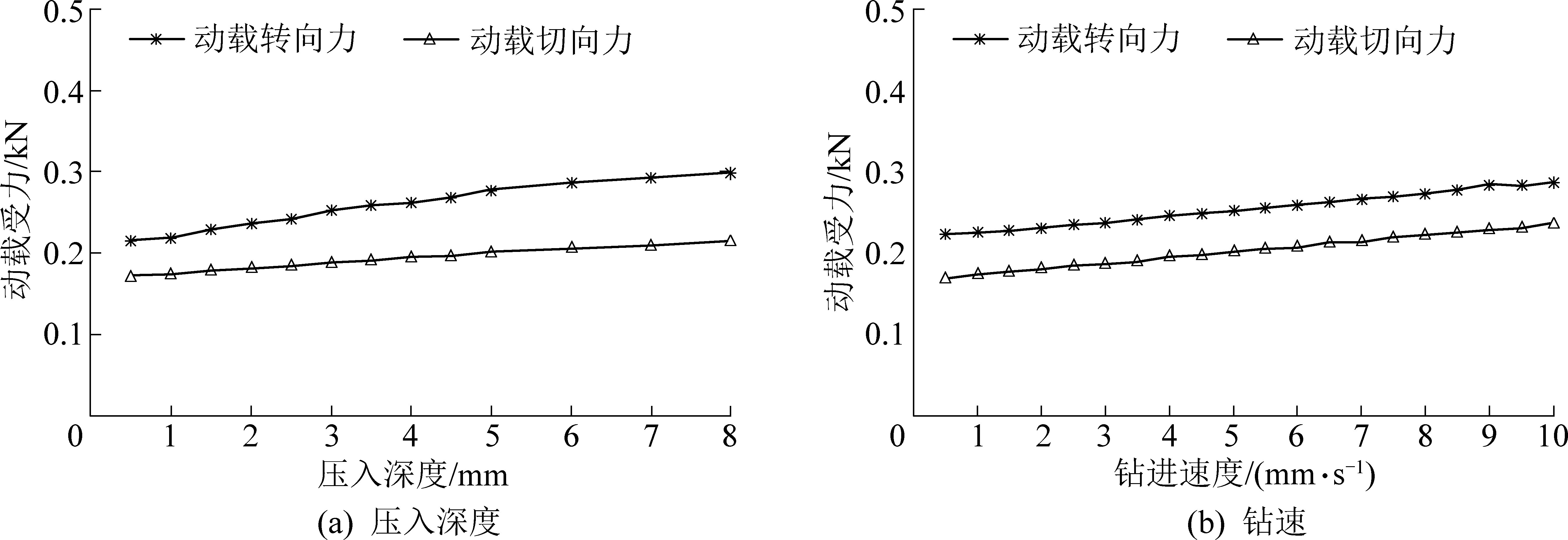
图2 典型煤层动载受力分析
Fig.2 Dynamic load analysis of typical coal seam
1.2 振动数学解析模型
通过分析钻柱系统在地层中的动载受力状态，可建立钻柱系统的动力学振动模型。 将整个钻柱系统沿其轴线离散化成有限个空间梁单元，动力学模型可以通过应变、惯性、阻尼以及作用力等虚功离散单元来构建，并将钻柱系统的轴向位移、切向位移和扭转角度离散化，建立的钻柱系统振动动力学模型如图3 所示。 图中表示钻柱系统在钻进过程中受到地层动载作用力，在反弹的同时还会发生可恢复的弹性形变，即产生横振、纵振和扭振。 k2 为系统连接刚度，c2 为系统阻尼，mn 为第n 个单元质量，k1n为第n 个单元连接刚度，c1n为第n/个单元阻尼，Ftn为第n 个单元切向力，Mdn为第n 个单元转矩。
式中：M 为整体质量矩阵；D 为整体阻尼矩阵；Ke为弹性刚度矩阵；Kg为几何刚度矩阵；x 为节点的X 向整体位移矢量；y 为节点的Y 向整体位移矢量；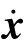
为节点的X 向整体速度矢量； 
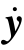为节点的Y 向整体速度矢量；x··为节点的X 向整体加速度矢量；y··为节点的Y 向整体加速度矢量； Ip 为微元段截面极惯性矩；δ 为节点的扭转角度矢量；
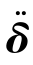为节点的扭转角加速度矢量。
根据边界条件和初始条件可以对振动数学解析方程组进行数值求解，得出钻柱系统的振动加速度解析表达式为
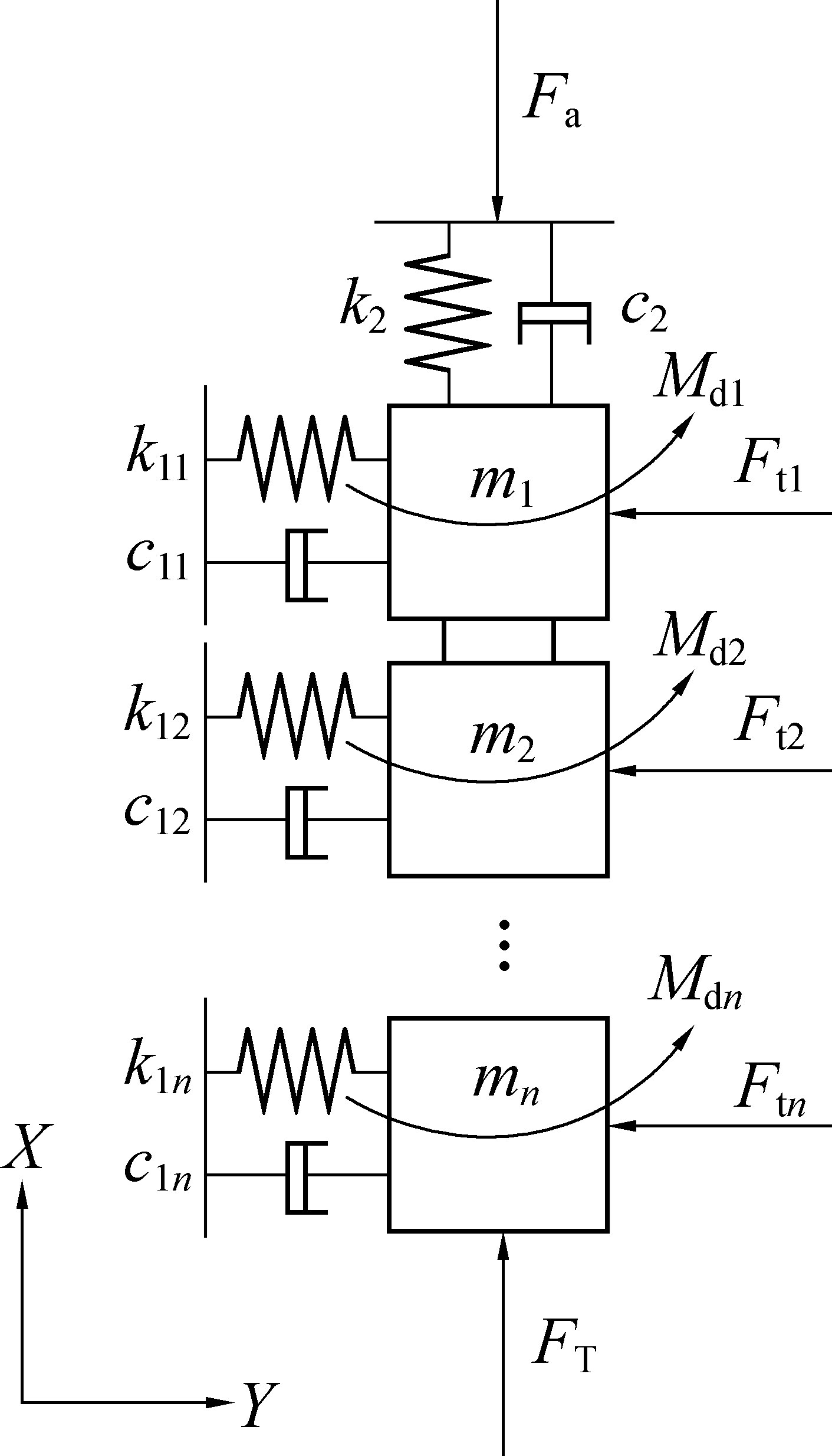
图3 钻柱系统振动动力学模型
Fig.3 Vibration dynamic model of drill string system
从式（15）—式（17）中可以得出，当x，t 为确定参数且钻探设备参数及动力条件不变时，钻柱系统振动加速度主要由钻速v、压入深度d 和地层特性决定。 结合煤矿巷道锚固孔回转钻进的工程背景，钻柱系统主要结构参数如下：
利用达朗伯原理可以解决该模型中非自由质点系的动力学问题，保证作用在每个质点的主动力、约束力和惯性力保持平衡，即建立的横振、纵振和扭振数学解析方程分别见式（12）—式（14）。
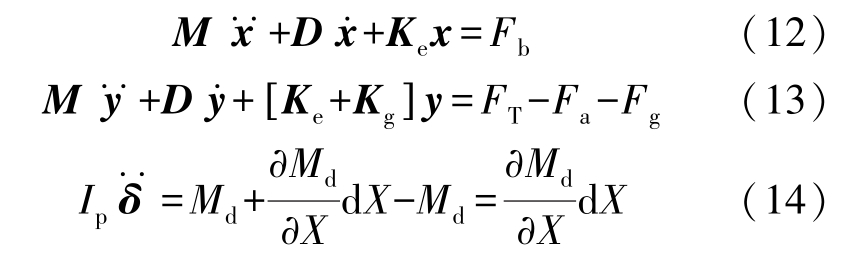
钻具总长度l/m 15
钻具密度ρ/（kg·m-3） 7 801
钻具阻尼ci/（N·s） 0.001
极惯性矩IP/ m4 1.536×10-6
钻具的剪切模量G/（N·m-2） 7.94×1010
由于锚固孔钻柱系统施工深度通常不超过15 m，钻柱系统总长度相对较小，则钻柱系统各质点转速相对稳定，扭转振动加速度稳定在0.01 rad/s2，数值较小且稳定，外界影响因素变化对其影响相对较小，在下文研究中不予考虑。
通过分析振动数学解析模型，含煤地层锚固孔施工中横向和纵向振动加速度是衡量含煤地层钻孔施工的重要信息。
当外界条件确定时，钻探施工参数中的钻速、钻压以及钻柱系统横向和纵向振动加速度可作为识别地层信息的指标，钻柱系统振动数学解析模型为进一步的数值仿真与实钻试验奠定了理论基础。
2 钻柱系统力学特性有限元仿真
2.1 仿真模型建立
通过ABAQUS 软件建立钻柱系统有限元分析模型，研究锚杆钻头在钻进典型含煤地层时的载荷变化规律。 在数值仿真中设置4 种典型岩样，分别为：①砂岩岩样；②煤层岩样；③均匀分布圆形孔洞的砂岩（以下简称孔洞砂岩）；④碎软煤样。 其中，后2 种岩样特别考虑空穴发育地层钻进和碎软煤层顺层钻进的工程背景。
锚杆钻头及岩样均采用SOLID 164 实体单元建模，以支持岩样的非线性特征。 锚杆钻头选用ø28 mm PDC 钻头，钻头体上焊接2 个ø13.44 mm×8 mm的复合片；立方体岩样尺寸为350 mm×350 mm×350 mm。 对PDC 钻头下端复合片附近以及岩样预破碎区域进行网格细化。 PDC 钻头采用四面体网格离散，其下端部网格尺寸为0.2 mm，上端部网格尺寸为0.5 mm；岩样形状规则，采用六面体网格离散，钻进区域150 mm×150 mm×350 mm 区域网格尺寸为0.5 mm，其余位置网格尺寸为1.5 mm，数值仿真三维模型如图4 所示。 特别考虑的孔洞砂岩模型与之后开展的实钻试验相一致，在岩石上均匀分布5×5个ø28 mm×350 mm 圆柱形孔洞，方向垂直于钻头钻进方向，如图4b 所示。
由于锚杆钻头的强度和硬度远高于岩样，因此钻头采用刚体材料模型，忽略其变形，以缩短计算时间。 弹塑性损伤剑桥本构材料模型综合考虑了材料硬化和软化的特点，能够很好地反映岩石在外载作用下的变形和损伤特性，因此岩样采用弹塑性损伤剑桥本构材料模型表示，当岩样体积变形达到其临界状态塑性常体积变形值时，岩样单元失效。 钻头和岩样的主要材料参数见表1。 由于碎软煤样失效应变极小，仿真时通过随机抽取若干个单元（单元数占据仿真岩体的80%），并赋予表1 中相应的参数加以表征。
钻进动态模拟计算中，设置岩样固定不动，约束其底端面及外周面的自由度，锚杆钻头以120 r/min的转速绕其中心轴线回转，并以8.3 mm/s 的速度向上钻进岩石。 对岩样四周施加非反射边界条件，已消除边界反射波的影响，模拟无限大的地层。 钻头与岩样之间设置侵蚀接触，保证岩样被破碎删除后其余的单元依然能够考虑接触。
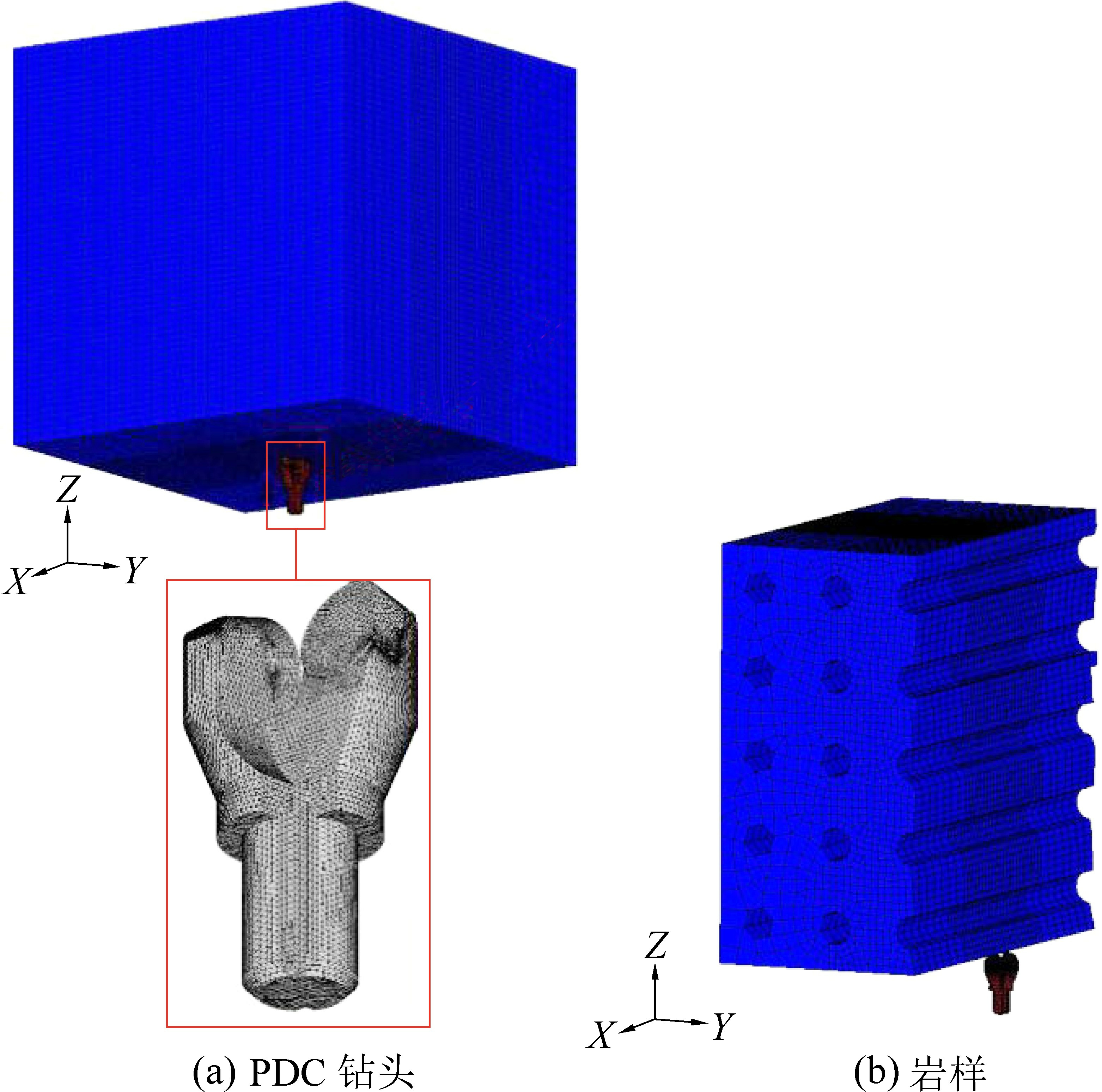
图4 PDC 钻头与岩样网格划分模型
Fig.4 Gird partition model of inner cone PDC bit and rock
表1 岩样与钻头材料参数
Table 1 Material parameters of rock and drillbit
量/GPa 泊松比 屈服极限/MPa弹性模 黏聚力/MPa内摩擦角/（°）砂岩岩样 2.76 2.45 0.25 0.98 27.50 24煤层岩样 1.39 0.43 0.35 0.15 1.80 20碎软煤样 1.18 0.35 0.30 0.05 1.20 25 PDC钻头3.56 8900.07 — — —
2.2 仿真结果分析
仿真应用有限元显式求解计算，钻进中钻头所受的轴向载荷是钻进破碎岩层时孔底岩层的反馈，径向载荷主要是钻柱维持正常保直钻进时孔壁岩层的反馈。 采用数据后处理软件对模拟结果进行统计分析，可以得出锚杆钻头分别钻进上述4 种岩样时钻进轴向载荷和径向载荷随时间变化曲线如图5、图6 所示。
分析图5 和图6 可知：①锚杆钻头钻进砂岩岩样、煤层岩样、孔洞砂岩和碎软煤样4 种典型岩样的平均轴向载荷分别为3 920.20、262.48、1 101.96、62.74 N。 虽然钻进孔洞砂岩时轴向载荷跳动较大，但平均值仍是砂岩岩样钻进时最高；碎软煤样较煤层岩样轴向载荷相差明显。 ②锚杆钻头钻进砂岩岩样、煤层岩样、孔洞砂岩和碎软煤样4 种典型岩样的平均径向载荷分别为142.74、22.60、526.32、3.17 N，径向载荷主要维持钻进平衡，钻进完整岩样的数值都在轴向载荷的10%以下，但钻进孔洞砂岩时的数值接近50%，整体曲线变化规律与轴向载荷类似。 ③锚杆钻头回转钻进岩石，随着岩石块体发生剪切崩碎，轴向载荷与径向载荷整体呈不规则跳跃变化。 ④煤层岩样钻进平均轴向载荷的仿真结果为262.48 N，参考图2 典型煤层动载受力分析图，在相同钻速条件下解析计算值为271.13 N，误差率为3.29%，达到设计要求。 同理可对砂岩岩样、孔洞砂岩和碎软煤样进行动载解析计算，并与仿真结果进行比较，结果基本保持一致。
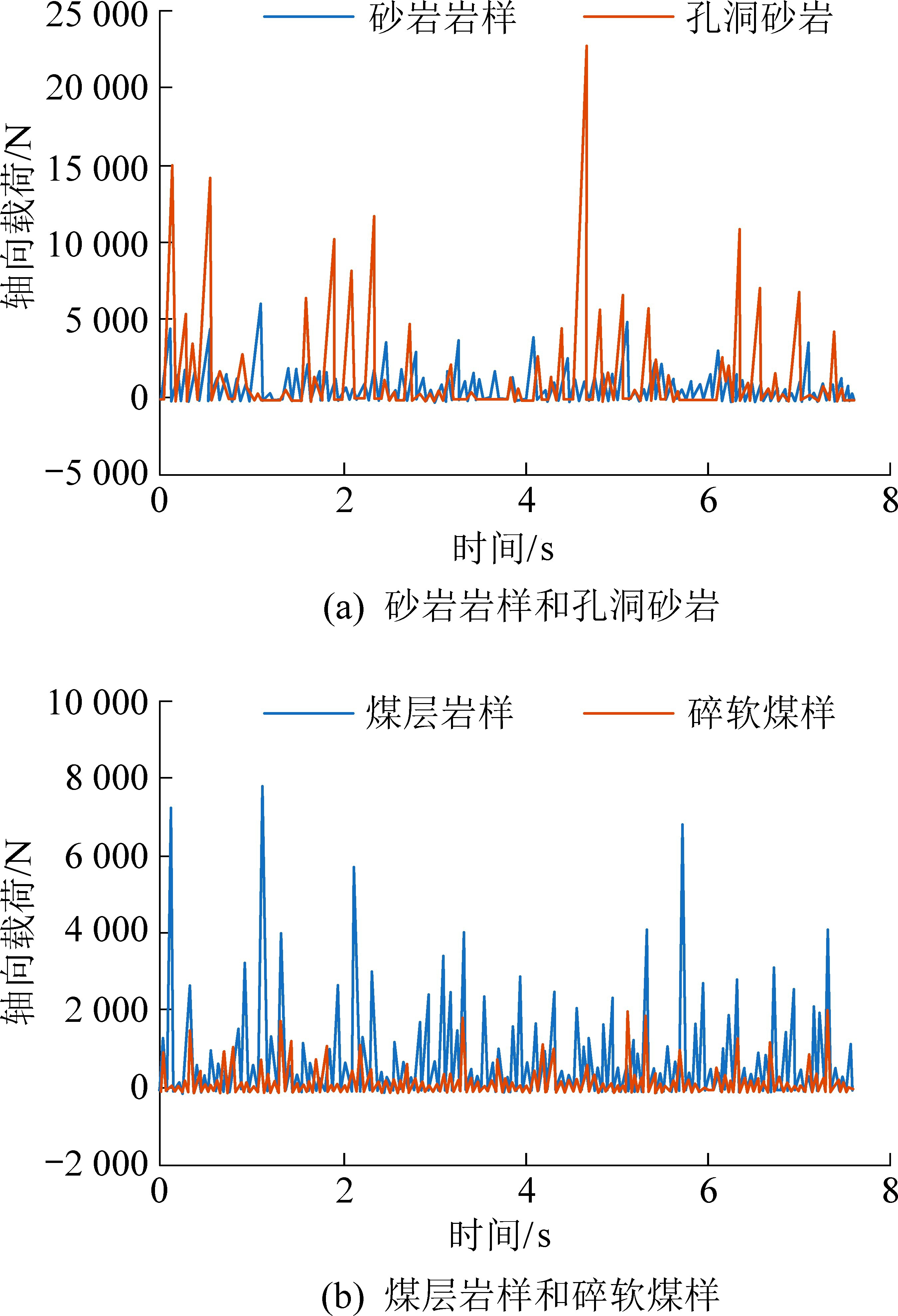
图5 轴向载荷变化曲线
Fig.5 Curve of axial load changing
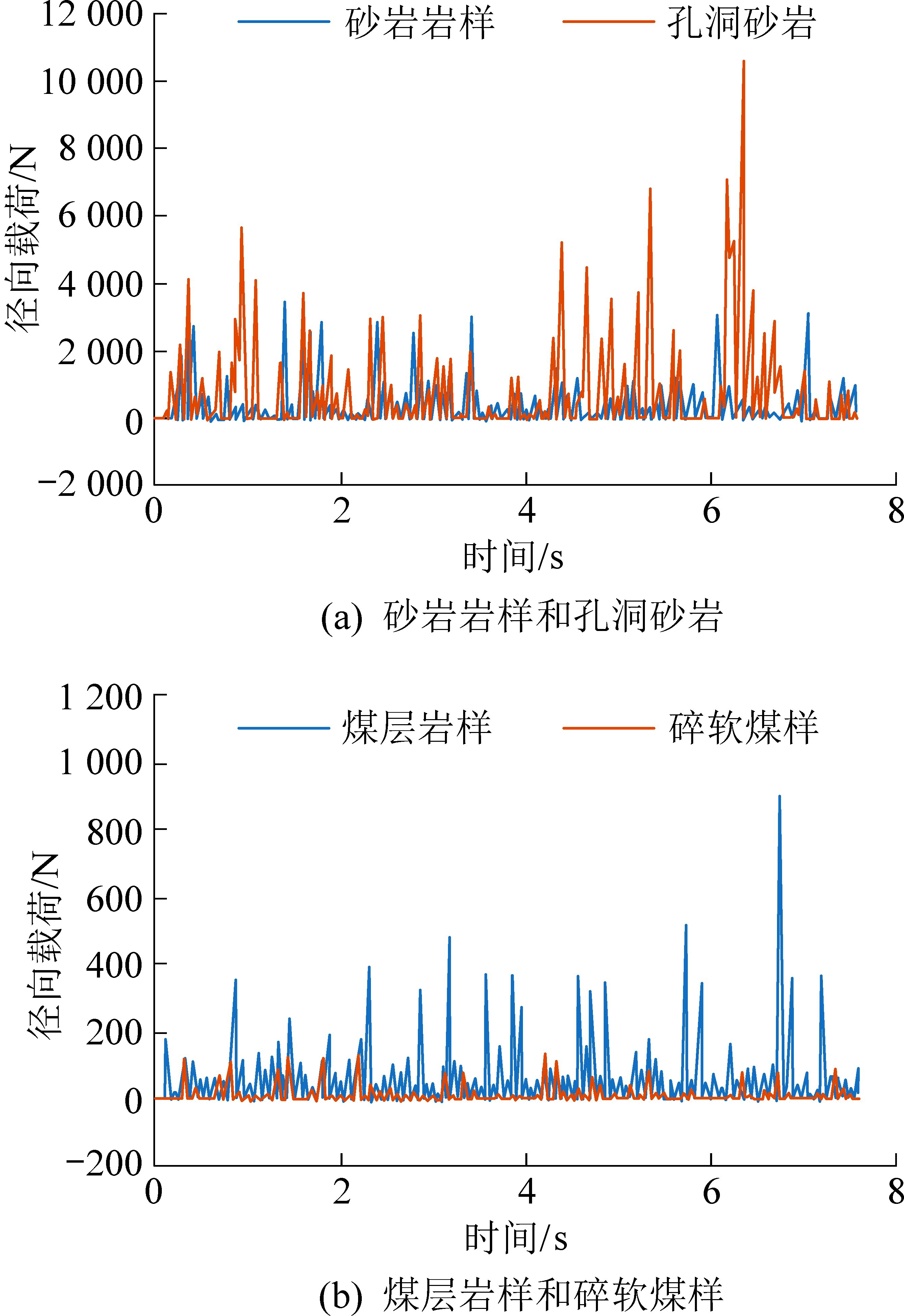
图6 径向载荷变化曲线
Fig.6 Curve of radial load changing
锚杆钻头钻进孔洞砂岩时纵向加速度随时间变化曲线如图7 所示。 钻头开始接触岩石并钻进碎岩时，加速度不断增加并产生较大幅值的振动变化；随着钻头钻入中间孔洞，加速度骤然降低，并趋于平缓。 根据加速度曲线剧烈变化能够判断钻头是否钻进孔洞，从而有效识别岩石特性变化。
图7 孔洞砂岩钻进纵向加速度变化曲线
Fig.7 Curve of acceleration of longitudinal vibration withhole sandstone drilling
根据有限元仿真结果，锚杆钻头的工作载荷面对强度不同的岩样时差别明显，这与解析结果相一致；针对空穴发育地层和碎软煤层顺层钻进的特殊钻进工况，锚杆钻头的载荷与加速度变化可用来指导现场钻进时地层的快速辨识。
3 实钻试验
3.1 试验条件与方法
钻进试验台由主机、泥浆泵、动力泵站、控制台以及各种附件组成，具有钻机电液控制，钻进参数实时监测功能，钻进试验系统如图8 所示。 其中，控制模块、数据采集模块与显示屏之间采用CAN 总线通信。 为监测振动信号，在动力头主动钻杆外部粘接了高精度陀螺仪、加速度计和地磁场传感器的BWT901 型传感模块，根据安装位置，钻杆纵向振动在z 向表现，横向振动分解为横截面x，y 两分量研究。 试验时钻机动力头直接驱动钻杆回转钻进，使用清水作为冲洗液来清除孔底岩屑和冷却钻头，钻进工艺参数可通过液压系统调节。 试验给定初始转速120 r/min，钻压0.8 MPa，泵量10 L/min。
图8 钻进试验系统示意
Fig.8 Schematic of drilling test system
根据相似材料模拟条件要求预制4 种试验岩样（图9），岩样材料选用复合硅酸盐水泥、中砂和粉煤渣，按照一定的比例在自然温度、湿度条件下养护浇筑成型，岩样尺寸为350 mm×350 mm×400 mm，同时利用LAW-1000 型电液伺服万能试验机对岩样进行了力学测试，并通过监测数据分别得到标准岩样的单轴抗压强度，保持与仿真模型一致。 孔洞砂岩岩样在整体砂岩岩样上通过等距离钻进，翻转90°后可预制完成。 碎软煤样采用圆柱状模具，煤样取自韩城矿区二叠系的山西组3 号煤层，岩石坚固性系数f 为0.1 ～0.3，煤体结构为碎粒煤和糜棱煤，用硅酸盐水泥浆浇注后静置养护完成。
3.2 试验结果分析
试验中采集频率为100 Hz，得出的典型岩样钻进纵向振动加速度信号如图10 所示。 由图10 可知：①钻进砂岩岩样时，采集到振动加速度幅值区间为-4.41～4.41 m/s2，钻进煤层岩样时的振动加速度幅值区间为-1.46～1.46 m/s2，而碎软煤样的振动加速度幅值区间为-0.275 ～0.275 m/s2，且三组信号的包络均比较平稳；②钻柱在碎软煤层的试样中回转钻进时，由于介质比较松软，各方向外界力使钻头平稳钻进，钻柱产生的振动信号幅值明显较小；③钻柱在砂岩试样中钻进时，硬度较大，所造成的钻柱振动会增大，且会产生幅值较大的瞬间高频脉冲信号。所以，利用振动信号的加速度幅值可初步判别所处典型岩样类别。
图9 4 种岩样示意
Fig.9 Schematic of four rock specimens
钻入孔洞砂岩时纵向与横向的响应信号变化规律如图11 所示。 开始钻进岩样时，产生幅值较大的瞬间高频脉冲信号，之后振幅趋于平缓，如图11a 中Ⅰ区域所示；钻入孔洞时，可见幅值的包络线有所降低，如图11a 中Ⅱ区域所示，然后再次钻入非空介质，产生幅值较大的脉冲。 岩样中共有5 个等距的孔洞，由图11 可知相应振幅较大的峰值点，对应刚钻入岩样非空层的振动信号。 峰值点的时间间隔基本均匀相等，且与试验过程中记录的介质层突变的时间点一致，说明实钻中通过振动时域信号的幅值变化，可有效识别钻入岩体空穴分布的情况。
锚固孔钻进中钻柱振动的主要震源为钻头破碎岩石产生的振动，钻柱与孔壁接触的影响较小，传递震源振动的过程中，钻柱传播效应很强。 当地层的岩性和构造发生变化时，会在幅值和变化规律上相应的产生变化。
图10 典型岩样钻进纵向振动加速度信号
Fig.10 Acceleration of longitudinal vibration signal
4 结 论
1）针对煤矿巷道顶板锚固孔钻进施工情况，完成了钻柱系统在含煤地层施工中的动载受力分析，得到了地层作用的动载轴向力和切向力的解析表达式，并分析了其变化规律。
2）基于有限单元法，利用达朗伯原理建立了非自由质点系的动力学模型，包括横振、纵振和扭振的数学解析方程组，并结合巷道支护工程参数计算可知，钻柱系统的横向和纵向振动加速度是钻孔施工中衡量含煤地层特性的重要指标。
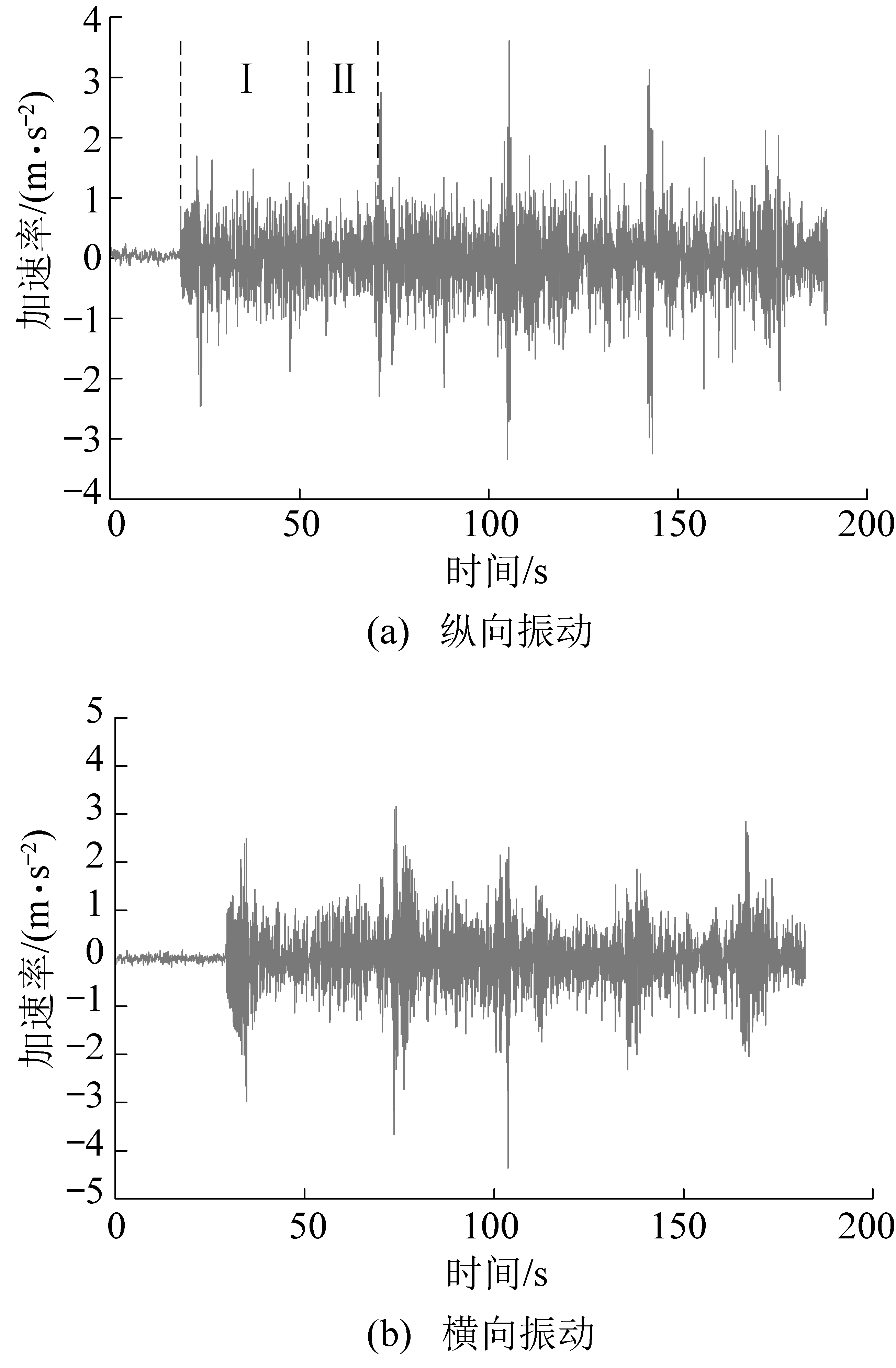
图11 孔洞砂岩钻进振动加速度信号
Fig.11 Acceleration of longitudinal vibration signal
3）通过建立砂岩岩样、煤层岩样、孔洞砂岩和碎软煤样等4 种典型岩样有限元模型，仿真分析得到锚杆钻头分别钻进4 种岩样时轴向载荷、径向载荷和加速度变化曲线，典型煤层轴向载荷仿真结果与解析解基本一致，并与岩石特性变化之间存在必然联系。
4）实钻试验结果表明，含煤地层锚固孔施工中振动加速度实时监测可有效识别典型含煤地层，尤其对于空穴发育地层和碎软煤层顺层钻进的特殊钻进工况时，识别效果良好。 下一步将结合高维钻进参数、地层图像等信息继续深入探索含煤地层岩性的精准识别，提高实用性，以期为煤矿井下巷道地层信息智能探测提供技术支撑。
［1］ 彭苏萍，孟召平. 矿井工程地质理论与实践［M］. 北京：地质出版社2002.
［2］ 袁 亮. 煤炭精准开采科学构想［J］. 煤炭学报， 2017， 42（1）：1-7.YUAN Liang. Scientific conception of precision coal mining［J］.Journal of China Coal Society， 2017， 42（1）：1-7.
［3］ 石智军，姚 克，姚宁平，等. 我国煤矿井下坑道钻探技术装备40 年发展与展望［J］.煤炭科学技术， 2020，48（4）：1-34.SHI Zhijun， YAO Ke， YAO Ningping， et al. Years of development and prospect on underground coal mine tunnel drilling technology and equipment in China［J］.Coal Science and Technol⁃ogy， 2020， 48（4）：1-34.
［4］ 王 琦， 秦 乾， 高 松， 等. 数字钻探随钻参数与岩石单轴抗压强度关系［J］. 煤炭学报. 2018， 43（5）： 1289-1295.WANG Qi， QIN Qian， GAO Song，et al. Relationship between pa⁃rameters while drilling and uniaxial compressive strength of rock［J］. Journal of China Coal Society， 2018， 43 （5）： 1289-1295.
［5］ 李 宁， 李 骞， 宋 玲. 基于回转切削的岩石力学参数获取新思路［J］. 岩石力学与工程学报， 2015， 34（2）： 323-329.LI Ning， LI Qian， SONG Ling. A new way of obtaining rock me⁃chanics parameters based on rotary cutting［J］. Chinese Journal of Rock Mechanics and Engineering， 2015， 34 （2）： 323-329.
［6］ 岳中琦. 钻孔过程监测（DPM）对工程岩体质量评价方法的完善与提升［J］. 岩石力学与工程学报，2014，33（10）：1977-1996.YUE Zhongqi. Improvement and improvement of engineering rock mass quality evaluation method by drilling process monitoring（DPM） ［ J］. Chinese Journal of Rock Mechanics and Engineering， 2014， 33 （10）： 1977-1996.
［7］ WANG Qi， GAO Hongke， YU Hengchang， et al. Method for measuring rock mass characteristics and evaluating the groutingreinforced effect based on digital drilling［J］. Rock Mechanics and Rock Engineering， 2019， 52（3）： 841-851.
［8］ YASAR E， RANJITH P G， VIETE D R. An experimental investi⁃gation into the drilling and physico-mechanical properties of a rock-like brittle material［J］. Journal of Petroleum Science and Engineering， 2011， 76（3）： 185-193.
［9］ 张幼振，徐信芯，阚志涛. 煤矿坑道回转钻进动力学研究现状与展望［J］. 煤炭科学技术， 2019， 47（1） ： 145-151.ZHANG Youzhen， XU Xinxin， KAN Zhitao. Research status and tendency on underground rotary drilling dynamics in coal mine［J］. Coal Science and Technology， 2019， 47（1）： 145-151.
［10］ 杨晓峰，康 勇，王晓川. 岩石钻掘过程钻头受力动力学解析模型［J］.煤炭学报， 2012， 37（9） ： 1596-1600.YANG Xiaofeng， KANG Yong， WANG Xiaochuan. Analytical dynamic model of the drill bit in rock drilling ［J］. Journal of China Coal Society， 2012， 37（9）： 1596-1600.
［11］ 张幼振， 张 宁， 邵俊杰， 等. 基于钻进参数聚类的含煤地层岩性模糊识别［J］. 煤炭学报， 2019， 44（8）：2328-2335.ZHANG Youzhen， ZHANG Ning， SHAO Junjie， et al. Fuzzy identification of coal-bearing strata lithology based on drilling parameter clustering［J］. Journal of China Coal Society， 2019，44（8）： 2328-2335.
［12］ MORADIS，RANJBARK. Experimental and computational failure analysis ofdrillstrings ［J］. Engineering Failure Analysis，2009，16（3）：923-933.
［13］ GUPTA SUNIT K， WAHI PANKAJ. Tuned dynamics stabilizes an idealized regenerative axial-torsional model of rotary drilling［J］. Journal of sound and vibration， 2018， 412：457-473.
［14］ 刘清友， 孟庆华， 庞东晓.钻井系统动力学仿真研究及应用［M］. 北京：科学出版社，2009.
［15］ 朱才朝，冯代辉，陆 波， 等.钻柱结构与井壁岩石互作用下系统耦合非线性动力学研究［J］.机械工程学报，2007，43（5）：145-149.ZHU Caichao， FENG Daihui， LU Bo， et al. Nonlinear study on dynamic action of integrated drill string-well rock system［J］.Journal of Mechanical Engineering， 2007，43（5）：145-149.
［16］ 刘永升，高德利，王镇全，等.斜直井眼中钻柱横向动态运动非线性模型研究［J］. 振动与冲击，2017， 36（24）：1-6.LIU Yongsheng， GAO Deli， WANG Zhenquan， et al. Study on nonlinear model of lateral dynamic motion of drill string in inclined straight hole［J］. Journal of Vibration and Shock，2017，36 （24）： 1-6.
［17］ 孟传明. 锚杆钻头破岩过程建模及仿真分析［J］. 煤炭科学技术，2013，41（10）：90-92.MENG Chuanming. Simulation analysis on rock cutting process of roof bolter bit［J］. Coal Science and Technology，2013，41 （10）：90-92.
［18］ 张幼振， 石智军， 邵俊杰. 煤矿巷道锚固孔钻进动力学仿真分析［C］/ /中国地质学会探矿工程专业委员会. 第十八届全国探矿工程（ 岩土钻掘工程） 技术学术交流年会论文集. 北京：地质出版社， 2015.
［19］ 刘少伟，付孟雄，张 辉，等.煤巷顶板锚固孔钻进钻杆振动机理与特征分析［J］. 中国矿业大学学报，2016，45（5）：893-900. LIU Shaowei， FU Mengxiong， ZHANG Hui，et al. Vibration mechanism and characteristics analysis of drill rod when drilling roof bolt hole［J］. Journal of China University of Mining ＆ Tech⁃nology，2016，45（5）：893-900.
［20］ 付孟雄，刘少伟，范 凯，等.煤巷顶板锚固孔钻进钻杆振动特性数值模拟研究［J］. 采矿与安全工程学报，2019，36（3）：473-481.FU Mengxiong，LIU Shaowei，FAN Kai，et al. Numerical simula⁃tion research on vibration characteristics of drill rod when drilling roof bolt hole［J］. Journal of Mining ＆ Safety Engineering，2019，36（3）：473-481.
［21］ JAMAL ROSTAMI， SAIR KAHRAMAN， ALI NAEIMIPOUR，et al. Rock characterization while drilling and application of roof bolter drilling data for evaluation of ground conditions［J］. Journal of Rock Mechanics and Geotechnical Engineering， 2015，7（3）：273-281.
［22］ 崔新霞，谭长均. 钻削机构与煤岩互作用系统耦合动力学研究［J］. 振动与冲击，2014，33（16）：97-104.CUI Xinxia， TAN Changjun. Coupling vibration of a drilling sys⁃tem with interaction between drilling mechanism and coal rock［J］. Journal of Vibration and Shock，2014，33（16）：97-104.
［23］ 李田军. PDC 钻头破碎岩石的力学分析与机理研究［D］.武汉：中国地质大学，2012.
［24］ 李夕兵. 岩石动力学基础与应用［M］. 北京：科学出版社，2014.
［25］ 孟召平，彭苏萍，傅继彤.含煤岩系岩石力学性质控制因素探讨［J］.岩石力学与工程学报，2002， 21（1）： 102-106.MENG Zhaoping，PENG Suping， FU Jitong. Study on control factors of rock mechanics properties of coal bearing formation［J］.Chinese Journal of Rock Mechanics and Engineering， 2002，21（1）： 102-106.
