0 引 言
煤层气作为一种清洁经济能源,其开采与利用一直备受关注[1]。 煤是一种多孔介质,孔裂隙是煤层气的储存和迁移通道。 煤岩孔裂隙网络具有典型的分形特征[2],其孔隙表面的变形、孔隙率及其大多物理性质均具有分形特征。 目前应用分形理论与煤岩的物性研究结合,可获得煤岩孔裂隙发育程度及其分布情况的定量信息。 高尚等[3]将液氮吸附法和压汞法相结合研究煤岩孔隙结构特征,并分别计算其分形维数。 邹俊鹏等[4]利用电子扫描数字图像对低阶煤的矿物含量、微裂隙发育情况及其形态特征进行了研究。 LIU 等[5]分析SEM 图像研究孔裂隙结构,发现多孔介质孔隙度与分形维数和渗透率均呈正相关关系。 许江等[6]研究发现煤岩变质程度与外部孔隙发育呈正相关关系。 YU 等[7]利用电子显微镜研究砂岩孔隙的几何特征及其分形参数,验证多孔介质的图像处理和分形是研究渗透率的一种有效方法。
为更准确地对煤层气开采过程中煤岩渗透率演化规律进行定量分析,国内外学者进行了大量试验与理论研究。 SEIDLE 等[8]提出以火柴棍模型解释煤岩渗透率与有效应力的关系,得到煤岩渗透率经验模型。 胡耀青等[9]发现煤岩的渗透系数随煤岩所受体积应力的增加而减小,随孔隙压力的增大而增加。 P&M 模型[10]和S&D 模型[11]是目前最有代表性的渗透率模型,基于此,LU 等[12]考虑三轴应力条件下的有效应力和基体吸附变形,建立不同边界条件下煤渗透性演化模型,并导出模型的5 个形式,通过现场数据对其进行验证。
综上所述,笔者选取贵州六盘水矿区煤岩,分别开展电镜扫描试验与孔隙压力升高的煤岩渗流试验,以研究煤岩孔裂隙结构分形特征及渗透特性。利用盒维数法[13]计算分形维数以表征煤岩表面复杂程度,基于恒定有效应力的渗流试验条件,以考虑分形效应的煤岩初始渗透率为中间桥梁,构建考虑孔裂隙分形特征的煤岩渗透率模型,通过试验验证其合理性,为深部煤层气开采和瓦斯灾害防治提供重要的理论支撑。
1 考虑孔裂隙分形特征的渗透率模型
1.1 渗流分形理论
通过分形几何建立考虑微观结构参数的煤岩渗透率模型,以分析孔裂隙微观结构对宏观渗透率的影响。 煤岩属多孔介质,其孔径分布中具有典型的分形特征,其孔隙累积数N 与孔隙直径η 服从如下的分形幂律关系[14]
式中:Df为孔裂隙分形维数;ηmax 为最大孔隙直径,μm;L 为直径尺度,μm。
对式(1)进行微分可得
式(2)给出了在η 和η+dη 区间里的孔隙数量,其中-dN>0。 从最小孔隙直径ηmin到最大孔隙直径ηmax的孔隙累计数Nt可由下式所得
由式(2)和式(3)可得
煤岩中气体运移通道也具有分形特征,可表示为[15]
式中:DT为迂曲度分形维数;L0是毛细管通道的直线长度,μm;Lt(η)是直径为η 毛细管通道的实际长度,μm,其中,Lt(η)不小于L0。 根据Hagene—Poi⁃seulle 方程,流体通过多孔介质煤岩中毛细管通道流量[16]q(η)可表示为
式中:Δp 为气体压力差,MPa;μ 为流体的动力黏性,Pa·s。
通过煤岩横截面积A 的总流量Q 为

煤岩属多孔介质,其ηmin/ηmax<10-2,式(7)可化简为
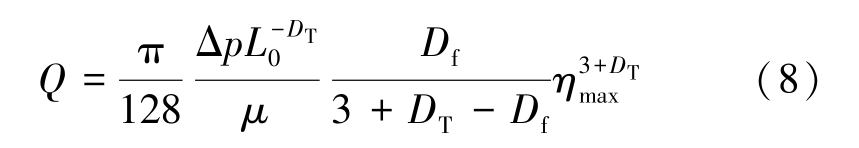
因而,煤岩初始渗透率可表示为
横截面中的孔可以被认为是具有不同直径η的圆。 此时总孔的横截面积Ap表示为
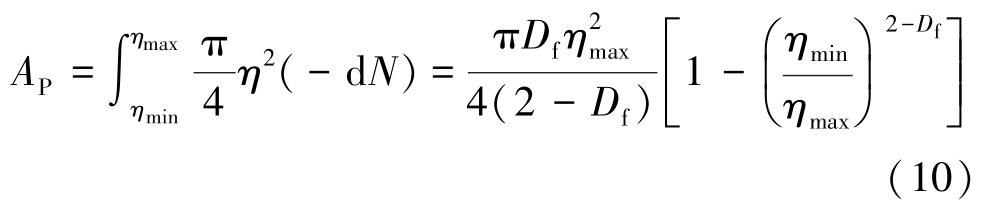
煤岩横截面积A 可表示为
式中:φ 为煤岩孔隙率。
将式(10)、式(11)代入式(9),则煤岩初始渗透率与孔裂隙分形维数的关系可表示为
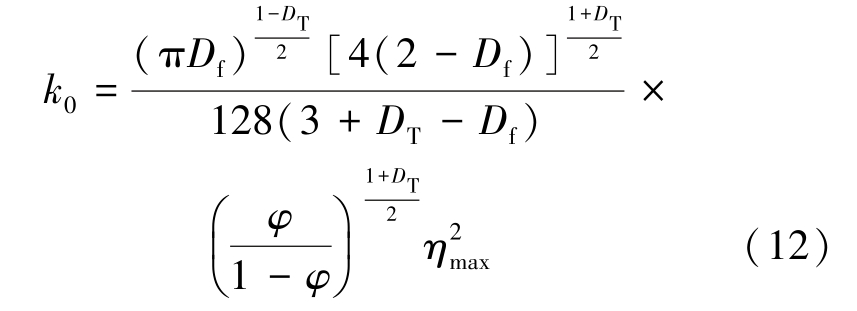
1.2 改进的渗透率模型
在三轴应力条件下进行瓦斯抽采,煤岩处于弹性变形阶段,考虑有效应力和煤基质膨胀变形的渗透率方程可表示为[12]
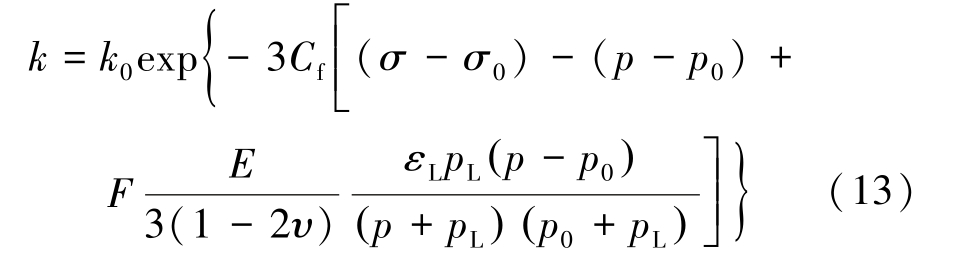
式中:F 为修正因子,取值0.255[17];E 为弹性模量,MPa;σ 为有效应力,MPa;σ0为初始有效应力,MPa;p 为孔隙压力,MPa;p0 为初始孔隙压力,MPa;Cf 为裂隙压缩系数,MPa-1;εL 为最大膨胀变形量,约为0.013;υ 为泊松比,取值0.2(四角田煤矿)、0.23(松河 煤 矿、 木 冲 沟 煤 矿); pL 为 吸 附 常 数, 取值1.57 MPa[18]。
其中,裂隙压缩系数Cf[19]可以表示为
式中:Cf0为初始裂隙压缩系数,MPa-1;α 为孔隙压力导致的裂隙压缩系数下降率,MPa-1。
煤岩孔隙率较低,微孔的含量较多,在气测过程中导致渗透率较理论值偏大。 考虑滑脱效应的渗透率k 为[17]
式中:ka 为煤岩绝对渗透率,10-3 μm2;b 为滑脱因子。
恒定有效应力条件下,存在(σ-σ0)-(p-p0)=0,进一步考虑滑脱效应影响,将式(13)代入式(15)得
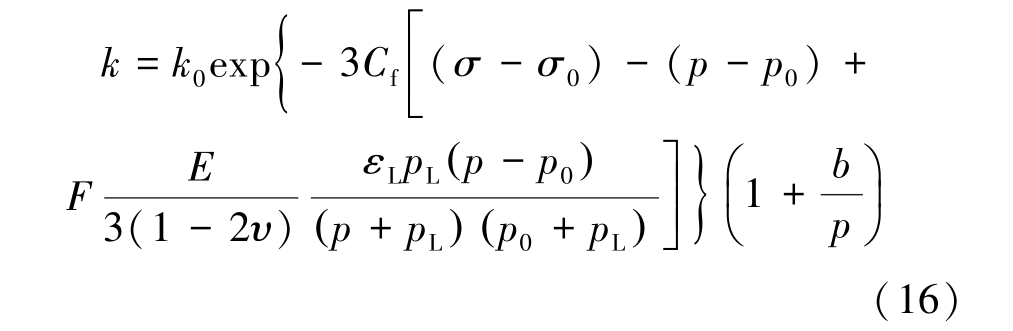
煤岩中的气体运移通道可近似为直线,即DT =1,将式(12)、式(14)代入式(16)可得考虑孔裂隙分形特征的煤岩渗透率模型为
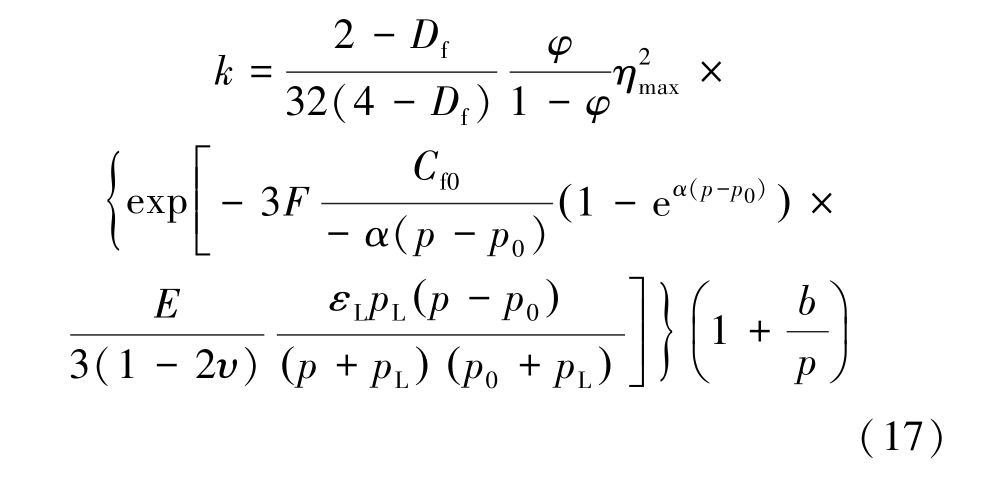
2 考虑煤岩孔裂隙结构的渗流试验
2.1 试样制备
为研究贵州六盘水矿区煤岩孔裂隙结构特征及渗透特性,选取煤岩为六枝矿区四角田煤矿7 号煤层、盘江矿区松河煤矿3 号煤层及水城矿区木冲沟煤矿8 号煤层的煤岩。 利用5E-MACIII 红外快速煤质分析仪对煤岩进行工业分析,均为变质程度较高的烟煤。 将取回的煤岩利用粉碎机粉碎,取一部分原煤块作为电镜扫描试验;另取一部分煤粉将其制成ø50 mm×100 mm 的煤样,用于孔隙压力升高的渗流试验。
2.2 电镜扫描
采用TESCAN VEGAⅡ型自带能谱扫描电镜,对六盘水矿区3 个煤层煤岩进行电镜扫描试验,得到不同放大倍数下能够清楚观察孔隙及裂隙结构的图像,分析煤岩的微观孔裂隙结构及其分布情况。电镜扫描时,应选择煤岩中平整的新断面作为观察面。 为保证效果,对样品进行真空镀膜处理,然后抽至真空。
2.3 三轴渗流试验
采用自主研制的出口端正压三轴渗流装置[20],进行恒定有效应力条件下孔隙压力升高的渗流试验。 试验中选取纯度为99.99%的CH4作为试验气体,通过改变轴压和围压来保持恒定平均有效应力为2.00 MPa,以消除应力影响。 将恒温水浴固定为30 ℃,出口瓦斯压力0.10 MPa,通过控制进口瓦斯压力改变孔隙压力,试件中的孔隙压力变化:0.35 MPa→0.55 MPa→0.75 MPa→0.95 MPa→1.15 MPa→1.35 MPa→1.55 MPa→1.75 MPa→1.95 MPa。 详细试验步骤见文献[17]。
3 试验结果及分析
3.1 SEM 图像
通过对六盘水矿区煤岩的电镜扫描,得到其在500、2 000、5 000 倍放大水平下的SEM 图像(图1)。

图1 煤岩表面扫描电镜图(5 000×)
Fig.1 Electron microscopy of coal rock surface(5 000×)
由煤岩SEM 图可知:四角田煤矿7 号煤层煤岩结构较致密,孔裂隙发育良好,具有2 条清晰的宽度较大的裂隙,并伴有大量交叉微裂隙及孔隙发育,孔裂隙间相互贯通,煤岩结构破坏严重。 松河煤矿3号煤层煤岩有1 条平行的宽度较大裂隙,结构致密,周围少见孔裂隙分布。 木冲沟煤矿8 号煤层煤岩整体为致密块状,无明显孔裂隙。 3 个煤矿煤岩孔裂隙结构存在明显差异,在相同的放大水平下出现形状、大小和长度各异的孔隙及裂隙,说明各煤岩的连通性存在差异。
3.2 煤岩偏光、分形分析
煤岩是一种分形体,其孔裂隙结构特征为统计规律上的自相似性。 借助分形理论可将图形图像用数字图像表征。 将四角田煤矿7 号煤层SEM 图像(图2a)导入偏光分析软件,得到煤岩孔裂隙结构如图2b 所示。 调整好该软件的正确标尺后,通过软件自动计算煤岩孔隙率[6]及孔隙半径。 将偏光得到的煤岩孔裂隙结构图导入分形软件,得到孔裂隙边界图,白色部分代表处理得到的孔裂隙边界如图2c所示。 依据盒维数计算原理,对孔裂隙边界图进行分析。 盒子的尺寸范围为8~32,调整参数即可获得盒维数。
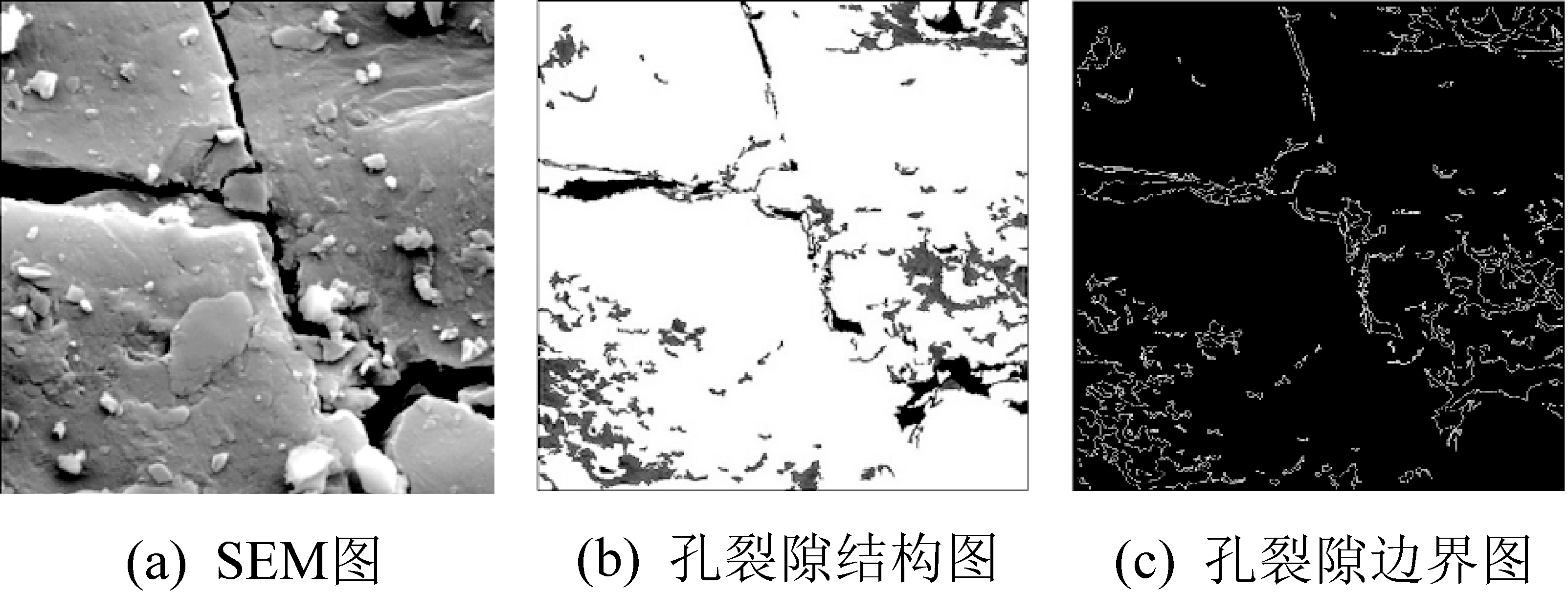
图2 四角田煤矿7 号煤岩孔裂隙分析过程示意(5 000×)
Fig.2 Crack analysis process of No.7 coal hole in Sijiaotian Coal Mine(5 000×)
在放大500、2 000、5 000 倍时,煤岩分形维数由大到小的顺序均为四角田煤矿7 号煤层煤岩、木冲沟煤矿8 号煤层煤岩、松河煤矿3 号煤层煤岩。 分形维数可以从侧面反映煤岩孔裂隙的发育情况[21]。四角田7 号煤层煤岩分形维数最大,表明其孔裂隙发育情况最为复杂,这与电镜扫描试验结果相符。 由煤岩孔隙率测试结果与上述煤岩表面孔裂隙分布分形维数分析可知,孔隙率与煤岩分形维数呈正相关关系。因此,分形维数可以很好地表征孔裂隙发育程度。
3.3 不同孔隙压力下的煤岩渗透特性
为探讨煤岩孔裂隙与渗透率之间的内在联系,根据上述试验方案进行渗流试验。 煤岩渗透率随孔隙压力的变化曲线如图3 所示。
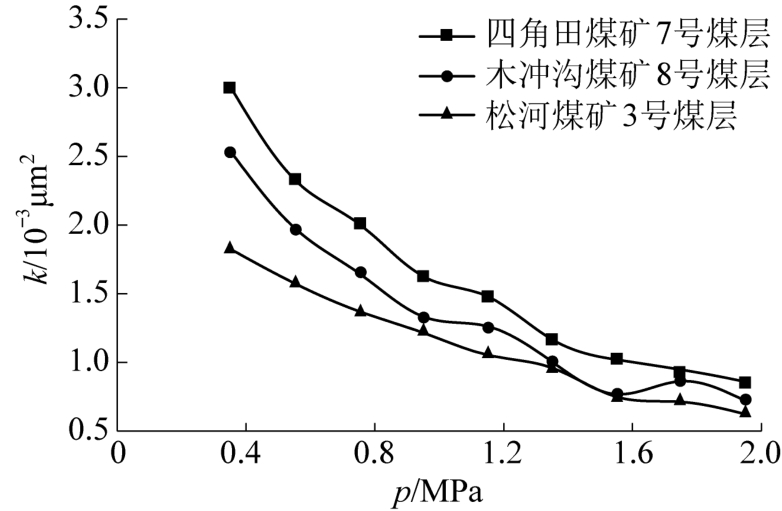
图3 煤岩渗透率随孔隙压力的变化关系
Fig.3 Curves of permeability of coal rock as a function of pore pressure
由图3 可知:在相同的孔隙压力下其渗透率存在明显差异,原始孔裂隙结构发育制约着渗透率的大小。 当有效应力恒定时,煤岩渗透率随孔隙压力升高呈先急剧降低后趋于平缓的趋势。 对渗透率演化规律进行探讨可知:一方面低孔隙压力下,煤的吸附作用较强,煤岩骨架发生内向吸附变形。 孔隙压力升高时吸附能力加强,孔裂隙吸附瓦斯层增厚,导致煤基质膨胀,使得瓦斯渗流通道变小。 另一方面孔隙压力较低时滑脱效应显著,随孔隙压力增大滑脱效应减弱,煤岩渗透率逐渐降低。 此外,随着孔隙压力的增大,煤的吸附作用趋于平衡,煤岩骨架膨胀变形也逐渐减小。
4 煤岩渗透率模型验证
为验证考虑分形特征的煤岩渗透率模型的合理性,将煤岩孔隙率φ、最大孔隙直径ηmax、分形维数Df代入式(12)可得煤岩初始渗透率k0。 进一步将所测的恒定有效应力、不同孔隙压力下的渗透率试验值和初始渗透率k0代入改进模型(式(17))。 同时与恒定有效应力下的渗透率模型LU 模型[12](式(13))进行对比。 不同渗透率模型与试验值对比曲线如图4 所示,两者模型参数见表1。
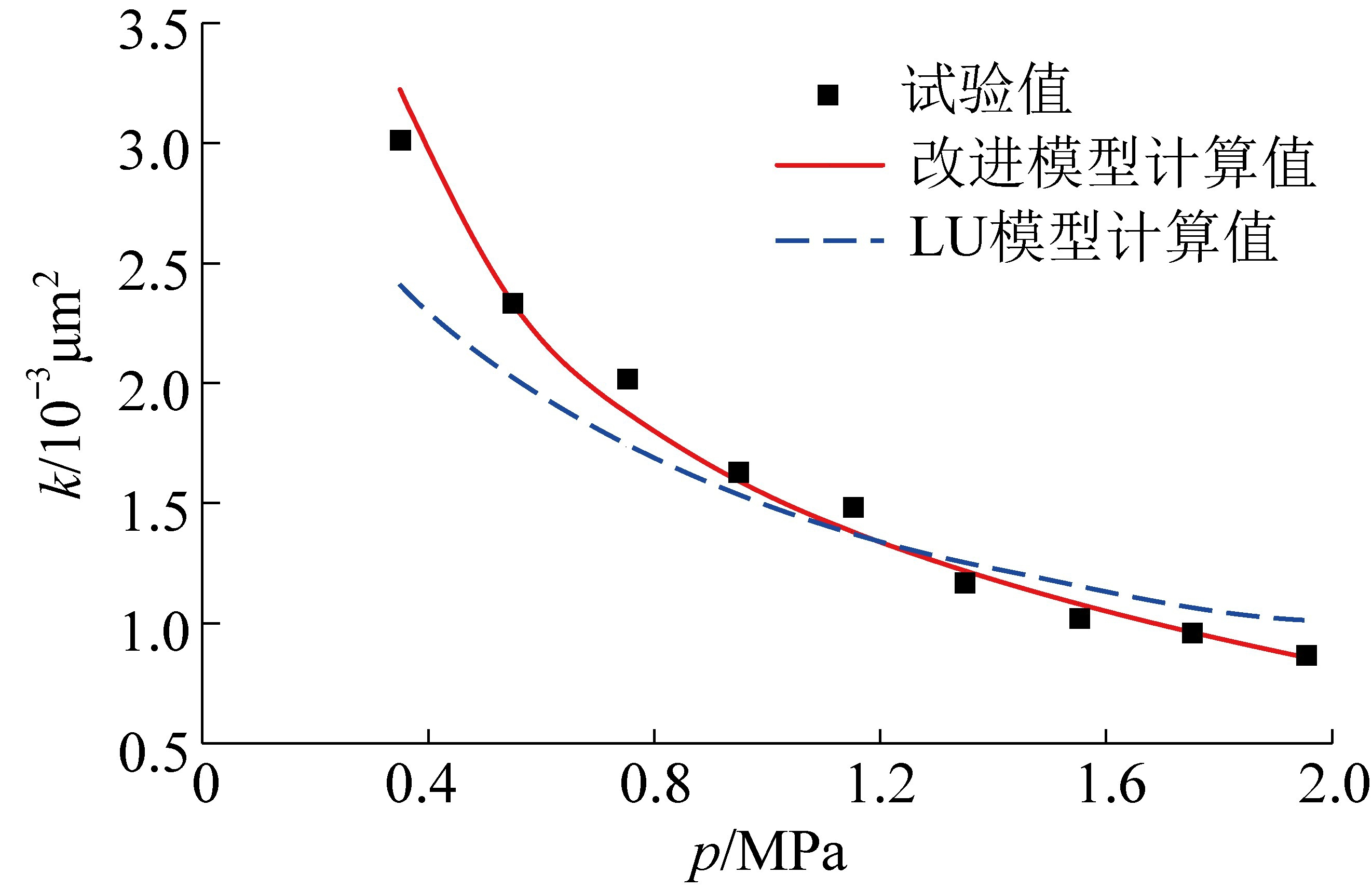
图4 四角田煤矿7 号煤层不同渗透率模型对比曲线
Fig.4 Comparison curves between different permeability models and experimental values in Sijiaotian No.7 coal seam
表1 模型参数对比
Table 1 Comparison of model fitting parameters

煤岩来源四角田煤矿7 号煤层木冲沟煤矿8 号煤层松河煤矿3 号煤层LU 模型参数Cf =1.667 2 Cf =1.311 0 Cf =1.166 9 γ=12.56% γ=12.57% γ=13.80%Cf0 =0.001 0 Cf0 =0.171 3 Cf0 =0.000 4改进模型参数a =0.578 1 a =0.966 0 a =2.856 5 b=0.495 6 b=0.995 4 b=2.340 1 γ=3.83% γ=5.57% γ=9.60%
由图4 和表1 可知:考虑孔裂隙分形特征的煤岩渗透率模型计算出的曲线与试验所测结果吻合得更好,且能很好反映恒定有效应力下孔隙压力与渗透率的变化关系。 而LU 模型未考虑孔裂隙分形维数以及滑脱效应,煤岩渗透率随孔隙压力变化不明显。 所建模型中分形理论可定量描述煤岩孔裂隙分布,为煤岩有效渗透率计算提供更加精确的方法,平均绝对误差γ 进一步表明改进渗透率模型的适用性。 因而,考虑孔裂隙分形特征的煤岩渗透率模型无论是理论机理的适用性还是对试验点的匹配方面都更加适用。
5 结 论
1)六盘水矿区煤岩孔裂隙连通性良好,具有明显的分形特征,且煤岩孔隙率与分形维数呈正相关关系。 当煤岩表面孔隙分布越复杂时分形维数越大,此时煤岩表面含有较多数量的微孔和大孔,良好的孔隙发育情况,有助于瓦斯在煤层间的储存与运移。
2)恒定有效应力条件下,随着孔隙压力升高,煤基质产生膨胀变形滑脱效应逐渐降低,此时煤岩渗透率呈先急剧降低后趋于平缓的趋势。 受孔裂隙结构影响,在相同孔隙压力条件下,原始孔裂隙结构发育不同,其渗透率也存在明显差异。
3) 建立了考虑孔裂隙分形特征的渗透率模型,所得渗透率计算值与实测值吻合度较高。 分形维数表征煤岩表面孔裂隙发育的复杂情况,孔隙度、渗透率与分形维数均呈正相关关系。
[1] HUANG Q,LIU S,WANG G,et al.Coalbed methane reservoir stimulation using guar-based fracturing fluid: a review[J].Journal of Natural Gas Science and Engineering,2019,66:107-125.
[2] JI W,SONG Y,JIANG Z,et al.Fractal characteristics of nanopores in the Lower Silurian Longmaxi shales from the Upper Yan⁃gtze Platform,south China[J].Marine and Petroleum Geology,2016,78:88-98.
[3] 高 尚,王 亮,高 杰,等.基于分形理论的不同变质程度硬煤孔隙结构试验研究[J].煤炭科学技术,2018,46(8):99-106. GAO Shang,WANG Liang,GAO Jie,et al.Experimental study on pore structure of hard coal with different metamorphism based on fractal theory[J].Coal Science and Technology,2018,46(8):99-106.
[4] 邹俊鹏,陈卫忠,杨典森,等.基于SEM 的珲春低阶煤微观结构特征研究[J].岩石力学与工程学报,2016,35(9):1805-1814.ZOU Junpeng,CHEN Weizhong,YANG Diansen,et al.Study on microstructure characteristics of low-rank coal in Hunchun based on SEM[J].Chinese Journal of Rock Mechanics and Engineering,2016,35(9):1805-1814.
[5] LIU K,OSTADHASSAN M,GENTZIS T,et al.Image analysis of the pore structures:An intensive study for Middle Bakken[J].Journal of Natural Gas Science and Engineering,2019,61:32-45.
[6] 许 江,袁 梅,李波波,等.煤的变质程度、孔隙特征与渗透率关系的试验研究[J].岩石力学与工程学报,2012,31(4):681-687.XU Jiang,YUAN Mei,LI Bobo,et al.Experimental study of rela⁃tionships between metamorphic grade,pore characteristics and per⁃meability of coal[J].Chinese Journal of Rock Mechanics and Engi⁃neering,2012,31(4):681-687.
[7] YU Q,DAI Z,ZHANG Z,et al.Estimation of sandstone permeability with SEM images based on fractal theory[J].Transport in Porous Media,2018,126:701-712.
[8] SEIDLE J P,JEANSONNE M W,ERICKSON D J.Application of matchstick geometry to stress dependent permeability in coals[R].SPE Rocky Mountain Regional Meeting,Wyoming,1992.
[9] 胡耀青,赵阳升,杨 栋,等.煤体的渗透性与裂隙分维的关系[J].岩石力学与工程学报,2002,21(10):1452-1456.HU Yaoqing,ZHAO Yangsheng,YANG Dong,et al.Relationship between permeability and fractal dimension of coal mass[J].Chinese Journal of Rock Mechanics and Engineering,2002,21(10):1452-1456.
[10] PALMER I,MANSOORI J.How permeability depends on stress and pore pressure in coalbeds:a new model[R].SPE Reserv.Eval.Eng.1998,1:539-544.
[11] SHI J Q,DURUCAN S.Drawdown induced changes in permeability of coalbeds:A new interpretation of the reservoir response to primary re⁃covery[J].Transport in Porous Media,2004,56(1):1-16.
[12] LU S,CHENG Y,LI W.Model development and analysis of the e⁃volution of coal permeability under different boundary conditions[J].Journal of Natural Gas Science and Engineering,2016,31:129-138.
[13] PIECHACZEK M,MIANOWSKI A.Coke optical texture as the fractal object[J].Fuel,2017,196:59-68.
[14] 郁伯铭.多孔介质输运性质的分形分析研究进展[J].力学进展,2003,33(3):333-346.YU Boming.Progress in fractal analysis of transport properties of porous media[J].Advances in Mechanics,2003,33(3):333-346.
[15] CHEN X,YAO G.An improved model for permeability estimation in low permeable porous media based on fractal geometry and modified Hagen-Poiseuille flow[J].Fuel,2017,210:748-757.
[16] PENG X,YU B.Developing a new form of permeability and Kozeny-Carman constant for homogeneous porous media by means of fractal geometry[J].Advances in Water Resources,2008,31(1):74-81.
[17] 李波波,杨 康,徐 鹏,等.力热耦合条件下煤岩渗透率模型研究[J].中国安全科学学报,2017,27(6):139-144.LI Bobo,YANG Kang,XU Peng,et al.Study on permeability model of coal and rock under thermal and thermal coupling condi⁃tions[J].China Safety Science Journal,2017,27(6):139-144.
[18] WU Y,LIU J S,CHEN Z W,et al.A dual poroelastic model for CO2 - enhanced coalbed methane recovery [ J]. International Journal of Coal Geology,2011,86(2/3):177-18.
[19] CONNELL L D,MAZUMDER S,SANDER R,et al.Laboratory characterisation of coal matrix shrinkage,cleat compressibility and the geomechanical properties determining reservoir permeability[J].Fuel,2016,165:499-512.
[20] 李波波,杨 康,袁 梅,等.不同温度下孔隙压力对煤岩渗流特性的影响机制[J].地球科学,2017,42(8):1403-1412.LI Bobo,YANG Kang,YUAN Mei,et al.Mechanism of pore pres⁃sure on coal flow seepage characteristics at different temperatures[J].Earth Science,2017,42(8):1403-1412.
[21] YAO Y,LIU D,TANG D,et al.Fractal characterization of seepagepores of coals from China:An investigation on permeability of coals[J].Computers and Geosciences,2009,35(6):1159-1166.
