0 引 言
我国煤层瓦斯含量丰富,瓦斯作为非常规天然气资源,具有极大的开采潜力和价值[1-2]。 然而,瓦斯也是煤矿动力灾害发生的主要因素之一,且其产生的温室效应为CO2的22 倍。 因此,煤层瓦斯抽采不仅可以降低煤矿瓦斯等温室效应气体的排放,而且还能降低与瓦斯相关的动力灾害事故的发生[3]。煤岩渗透率是研究煤层瓦斯抽采、优化钻孔布置及提高瓦斯抽采率的关键指标之一[4-5]。
国内外学者对煤岩渗透率进行了大量相关的试验、理论及数值模拟研究,提出了相关的渗透率模型,并对渗透率模型进行验证或应用。 文献[6]基于弹性理论最早提出了考虑瓦斯吸附应变和瓦斯压力的渗透率模型。 基于此,文献[7-8]建立了指数函数型的渗透率模型(S&D 模型)。 文献[9]从应变角度构建了煤岩体渗透率和孔隙率的立方函数式(P&M 模型)。 文献[10]构建了考虑瓦斯吸附变形影响的渗透率模型(C&B 模型),且在特定条件下此模型还可转化为S&D 或P&M 模型。 文献[11-13]假设煤岩体是双孔介质,分别对煤岩基质孔隙系统与裂隙系统建立了各自的孔(裂)隙率与(基质、裂隙)渗透率模型。 目前,比较经典的渗透率模型绝大部分以煤储层或煤层气开采为研究背景,且大部分都是基于上覆应力恒定、单轴应变及弹性变形的假设,从孔隙率变化(或应变变化)和应力状态变化的2 个角度建立。 而煤体实际的赋存处于三向应力状态,在煤矿开采扰动下,应力与瓦斯压力的变化对于煤体裂隙及渗透率的影响是不能忽略的。 基于煤层气储层为研究背景所建立的渗透率模型已不能很好地反映三向应力作用下煤体的渗流变化规律。 因此,在实际的煤矿地下开采过程中除了需要考虑瓦斯压力对煤体渗透率的影响外,需探讨三向应力作用下煤体的渗透率演化规律。
笔者将煤岩的结构进行简化,从应变的角度分析了瓦斯压力和三向应力作用对煤体裂隙变形及渗透率的影响,分别建立瓦斯压力-裂隙耦合和三向应力-裂隙耦合影响下煤体的渗透率演化模型,并结合前人的试验数据对构建的渗透率模型进行验证,以期为煤与瓦斯共采提供理论指导。
1 瓦斯压力-裂隙耦合对煤体渗透率影响分析及模型建立
1.1 瓦斯压力-裂隙耦合对煤体渗透率影响分析
国内外学者在瓦斯对煤体渗透率演化的作用及影响机理方面进行了大量试验研究和理论分析,主要从瓦斯压力和煤体基质吸附膨胀变形2 个方面分析。 目前国内外学者广泛接受的观点为:瓦斯压力的变化引起煤体有效应力的变化及煤体基质吸附膨胀变形,从而引起煤体渗透率的变化,这两者对煤体渗透率的影响处于相互竞争的关系。 大量的试验及工程案例表明,在恒定外部应力条件下煤体渗透率随瓦斯压力的增大呈现“V”型演化规律,这正是瓦斯压力和吸附变形相互影响造成的。 一方面,随着瓦斯压力的增加,煤体所受有效应力减少,煤体裂隙的开度增加,从而引起渗透率增加;另一方面,煤体基质的吸附膨胀变形随着瓦斯压力增大而增大,从而对裂隙产生挤压,引起裂隙宽度的减小,造成煤体渗透率的减小。 所以瓦斯压力对煤体渗透率的影响效果取决于占据主导地位是有效应力还是吸附变形。
1.2 基于瓦斯压力-裂隙耦合的煤体渗透率模型构建
煤体是由煤体基质和其内部的孔裂隙系统组成,其中煤体基质又包括骨架和其内部的孔隙[11-13]。 对煤体的结构进行简化(图1)。 假设煤体为各向同性弹性体,煤体基质被正交的节理裂隙均匀分割成正方体型单元体,煤体基质单元体的初始宽度为a0,均匀裂隙的初始宽度为b0。
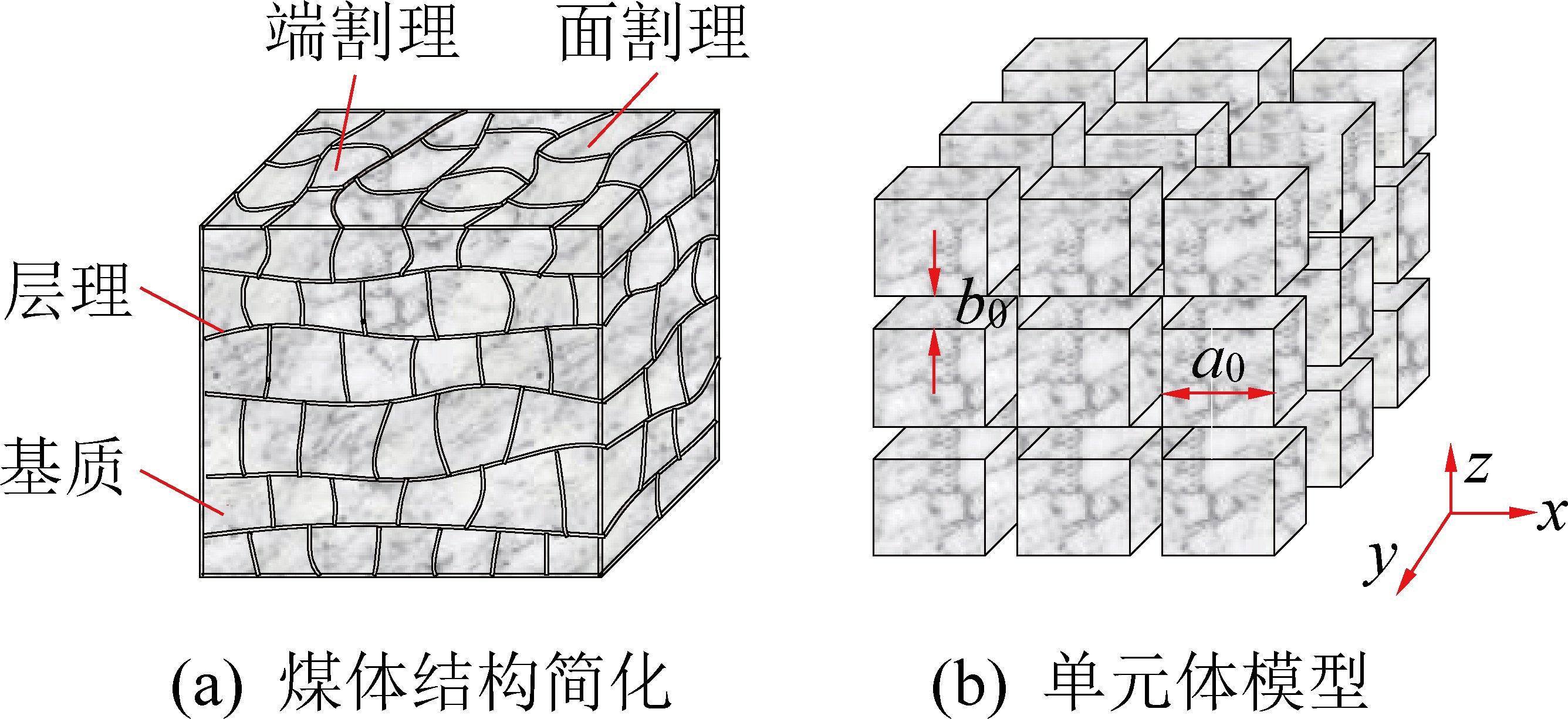
图1 煤体结构简化及单元体模型
Fig.1 Simplified coal structure and unit cell model
以图1 中红色虚线框所示的单元为研究对象。煤体内部裂隙的变形包含由瓦斯压力引起的变形和由煤体基质的吸附膨胀所引起的变形[6]。 故裂隙的宽度变化可表示为:
式中:Δbf、Δbs分别为瓦斯压力和煤基质吸附作用引起的裂隙宽度的变化量,m。
在恒定外部应力条件下,Δbf可表示为[14]
式中:Δpf为瓦斯压力变化量,MPa;En为裂隙弹性模量,MPa。
煤体基质吸附膨胀变形不仅对裂隙变形产生影响,还会引起煤体体积的膨胀。 因此,将煤体基质吸附膨胀变形全部等同于裂隙的压缩变形势必会高估吸附作用对煤体渗透率的影响,与试验数据产生较大的出入。 基于此,文献[15]考虑了煤体吸附过程中煤体基质与裂隙之间的变形关系,将煤体基质吸附膨胀变形划分为内膨胀变形和外膨胀变形2 个部分,只有内膨胀变形对裂隙宽度产生影响从而影响渗透率的变化,从而进一步完善和揭示了煤体基质吸附变形对渗透率的影响机理。 文献[16]用内膨胀系数FI来表征煤基质内膨胀应变与总吸附膨胀应变的比值,在此采用同样的做法来表征吸附对裂隙宽度的影响,故Δbs 表示为
式中:Δεs为吸附体应变的变化量,%;a 为煤基质单元体边长尺寸,m。
根据孔隙率的定义,煤岩裂隙的孔隙率φf可表示为[17]
式中,b 为煤基质体间的裂隙宽度,m。
化简式(8),由于b<<a,为简化运算,可以略去b 的高阶项,可得
再结合煤体基质吸附膨胀变形满足Langmuir吸附平衡方程,可得
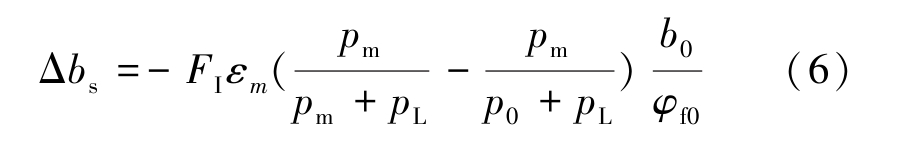
式中:pm为吸附瓦斯压力,MPa;p0为初始瓦斯压力,MPa;φf0为煤体初始裂隙孔隙率;εm 和pL 为等温吸附变形常数。
结合式(1)、式(2)和式(6),可以得到瓦斯作用下煤体裂隙宽度的变化量为
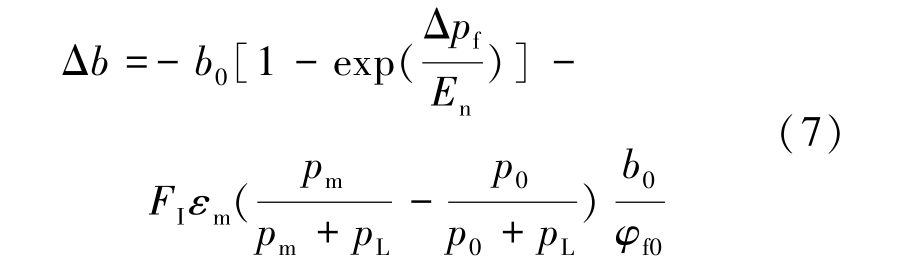
煤体的渗透率k 与裂隙宽度之间的关系为[17]
其中:ξ 为单位横截面积煤的裂隙长度之和(或裂隙曲率),m-1。 ξ 随应力变化程度远小于裂隙宽度变化程度,因此可假设ξ 值基本保持不变。 将式(8)进行变换可得
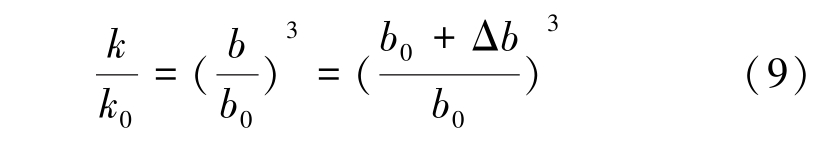
式中,k0为煤体初始渗透率,m2。
将式(7)代入式(9)可得基于瓦斯-裂隙耦合的煤体渗透率模型表达式为
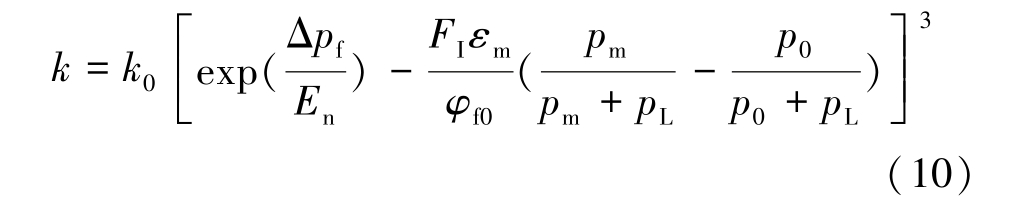
1.3 基于瓦斯压力-裂隙耦合的煤体渗透率模型验证
通常将内膨胀系数FI 看成常数来进行计算。在此,仍将FI作为常数,采用文献[18-19]的试验数据对建立的模型进行验证,模型所需的参数见表1,裂隙弹性模量En和文献[19]试验中pL和εm的数值通过模型匹配试验数值而得到。 煤岩渗透率测试试验均在瓦斯吸附平衡状态下进行,即在该过程中裂隙瓦斯压力与孔隙瓦斯压力相等。 模型的计算值与试验数据的对比结果如图2 所示,可以看出模型计算值与试验数据吻合度较高,验证了模型的可靠性,也说明在恒定外部应力条件下,内膨胀应变系数可以看成常数。
表1 模型参数
Table 1 Model parameters
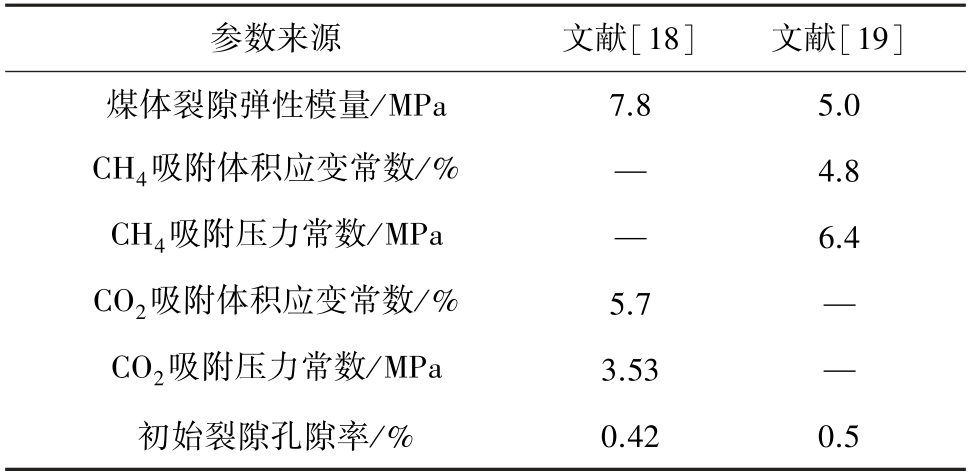
参数来源 文献[18] 文献[19]煤体裂隙弹性模量/MPa 7.8 5.0 CH4吸附体积应变常数/% — 4.8 CH4吸附压力常数/MPa — 6.4 CO2吸附体积应变常数/% 5.7 —CO2吸附压力常数/MPa 3.53 —初始裂隙孔隙率/% 0.42 0.5
由图2 可知,在煤体渗透率随瓦斯压力变化降至最低点之前,吸附作用占据主导地位,煤体基质吸附膨胀变形对渗透率的影响大于有效应力,随着瓦斯压力的增大,煤体渗透率逐渐减小;而在煤体渗透率最低点之后,有效应力占据主导地位,有效应力对渗透率的影响大于煤体基质吸附膨胀变形,随瓦斯压力增大,煤体渗透率增大。
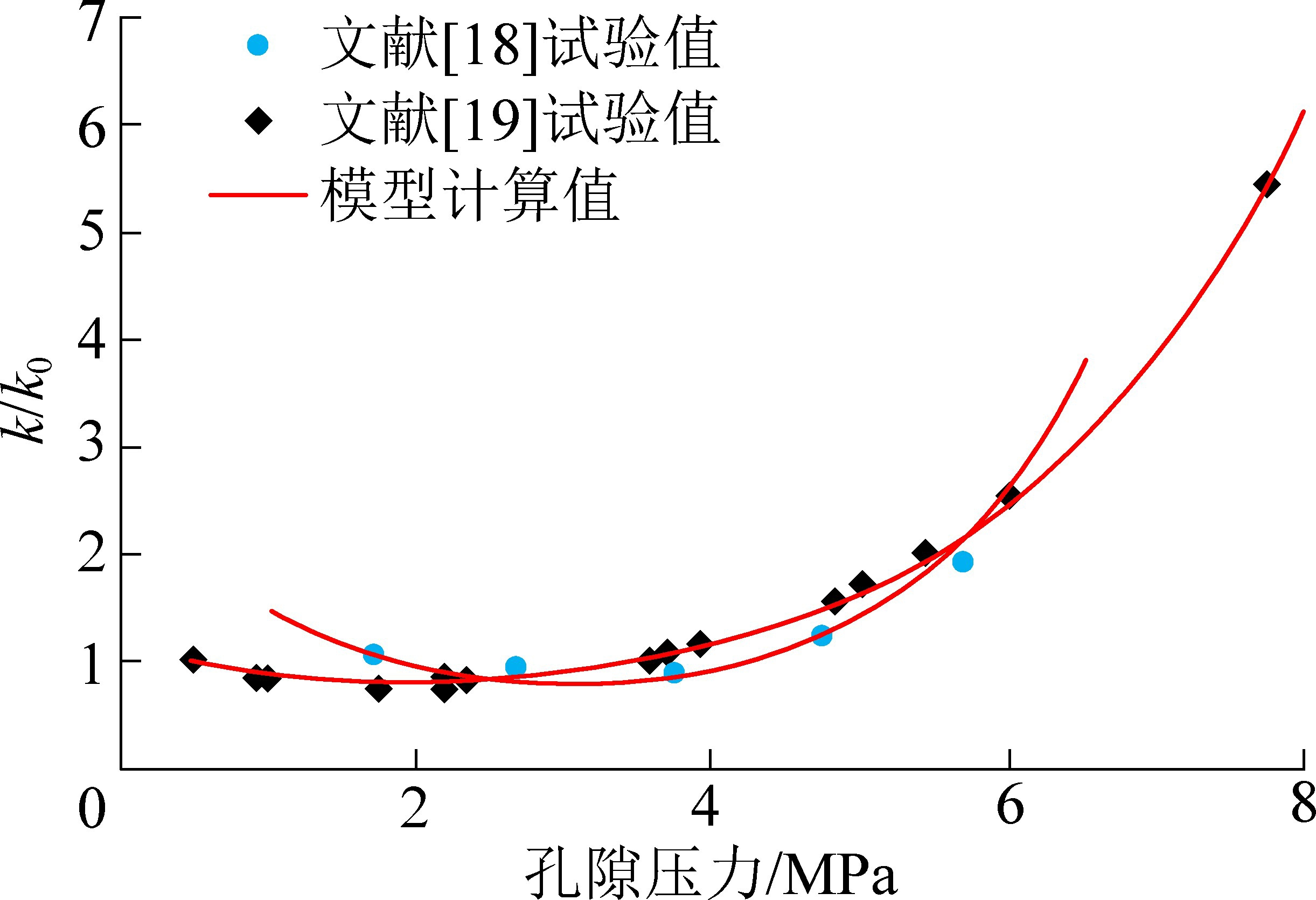
图2 模型计算值与试验值对比
Fig.2 Comparison of calculated values and experimental values of the models
2 应力-裂隙耦合对煤体渗透率影响分析及模型建立
2.1 应力-裂隙耦合对煤体渗透率影响分析
煤层渗透率-应力关系与裂隙岩体渗透率-应力关系相似[20],可借鉴岩石力学领域在三向应力作用下裂隙岩体渗流-应力耦合方面的研究成果。 在三向应力作用对裂隙岩体渗流的影响方面,国内外学者做了大量研究,从不同的思路和方法考虑三向应力对裂隙岩体渗流的影响,建立了裂隙宽度与渗透率或渗透系数之间的数学表达关系式,但对于侧向应力对裂隙变形的影响效果仍未形成统一的认识。 总体而言,针对考虑侧向应力对裂隙变形影响的做法可以归结为2 类,一类是将侧向应力等效为裂隙的法向应力直接作用于裂隙[21-22],另一类则是考虑应力引起基质岩块的变形与岩体的变形之间的关系求得裂隙的变形[23-24]。
2.2 基于应力-裂隙耦合的煤体渗透率模型构建
对于将侧向应力等效为法向应力这一做法,文献[25]通过简化模型并基于理论分析与推导得到侧向应力仅会引起法向应力方向的法向变形,并不会产生沿法向应力方向的等效应力,直接将侧向应力等效为法向应力的做法有待商榷和考证。 更多学者则从弹性力学的角度出发,尝试根据裂隙岩体变形与基质岩块变形之间的变化关系来反映裂隙的变化。 单裂隙岩体在三向应力作用下的变形情况如图3 所示,岩体由基质岩块和裂隙组成,则岩体的变形、基质岩块变形及裂隙的宽度变化之间的变化关系满足:
式中:Δεw、Δεg分别为岩体应变的变化量和基质岩块应变的变化量。
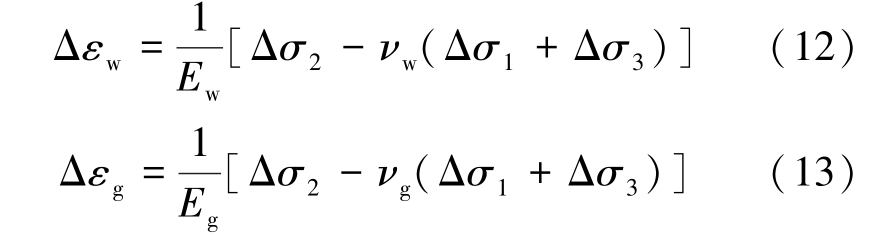
式中:Ew、Eg 分别为岩体和基质岩块的弹性模量,MPa;Δσ1、Δσ2 和Δσ3 为3 个方向应力的变化量,MPa;νw、νg分别为岩体和基质岩块的泊松比。
由孔隙率的定义,单裂隙岩体满足
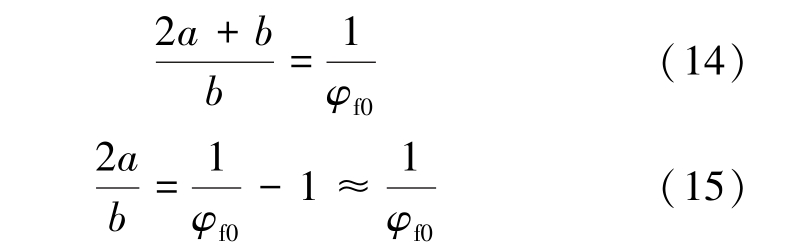
将式(12)—式(15)代入式(11)得
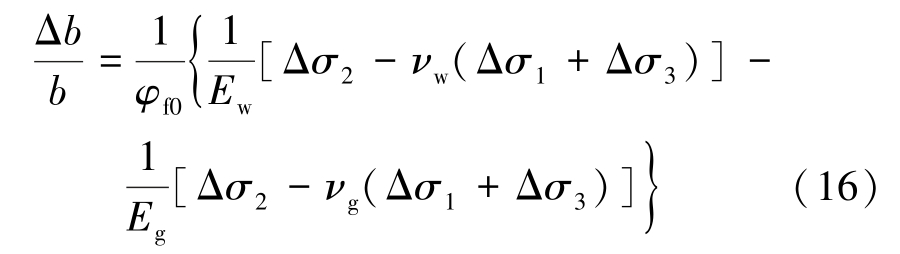
从形式上看,裂隙的变形由岩体与基质岩块的泊松比和弹性模量4 个力学参数来决定。 对此,部分学者为了简化运算认为νg =νw,则式(16)可写为
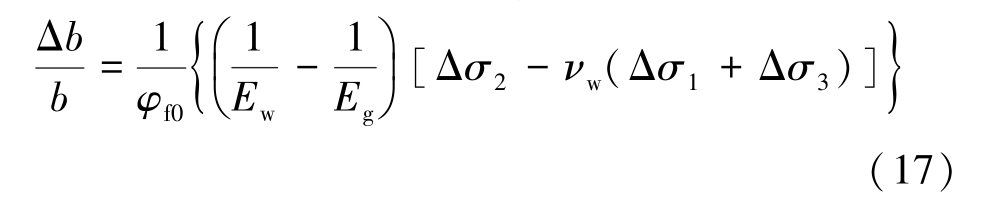
根据式(9)可得单节理岩体的渗透率表达式:
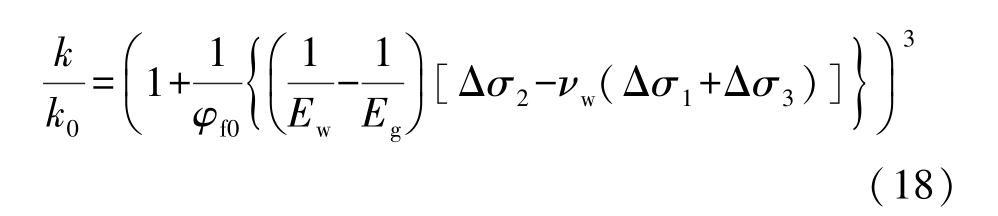
式(18)简化νg =νw后会使法向应力不变,仅在侧向应力作用下,出现随侧向应力增大和渗透率增大的情况,显然不符合实际的渗流规律。 如文献[26]推导了与式(18)相似的煤体渗透率模型,用该模型验证煤岩常规三轴压缩渗流试验时,在弹性阶段出现实际渗透率减小而理论计算渗透率增大的情况。 由于煤体裂隙宽度的变化对围压的敏感性大于轴压,围压和轴压在相同的变化量下,围压对裂隙变形的影响占据主导作用,煤体泊松比与煤体基质泊松比之间的差异引起的变化可以忽略;在三轴压缩试验中,煤岩在弹性阶段均表现为随轴向应力的加载其径向变形受压膨胀增大而渗透率降低,轴向应力作用下煤岩变形情况可简化为图4;可以看出煤体基质的泊松比大于煤体的泊松比,渗透率的变化正是由煤体泊松比与煤体基质泊松比之间的差异对裂隙宽度产生影响所造成的,此时这两者之间的差异是不能忽视的。 所以式(18)不能描述常规三轴压缩下煤体的渗透率变化。
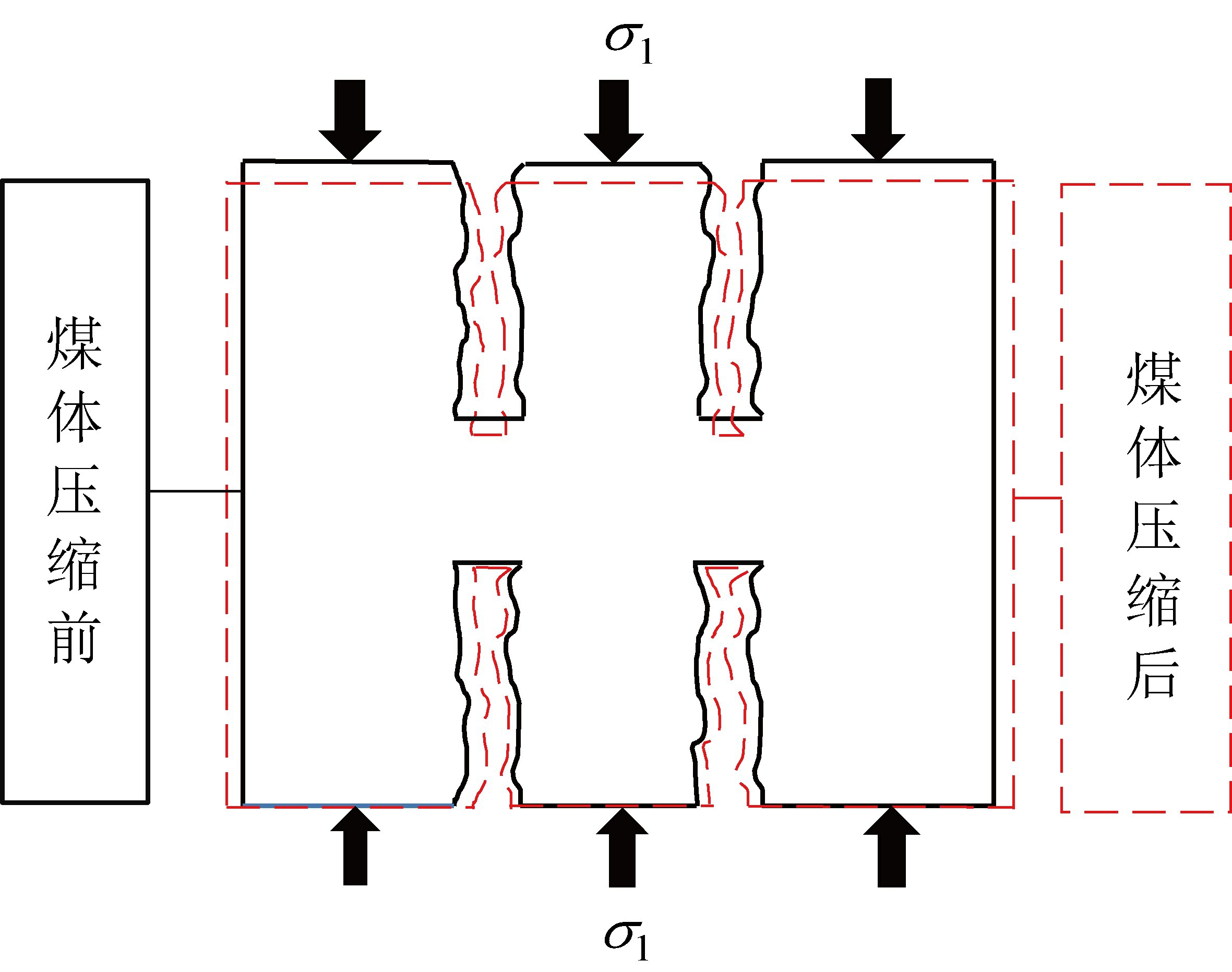
图4 侧向应力作用下煤体变形情况
Fig.4 Coal deformation under axial stress
侧向应力作用下,煤体骨架变形一部分用于向外膨胀,表现为煤体的法向膨胀变形,另一部分向裂隙方向膨胀,引起裂隙的压缩变形(图4)。 由于轴向应力作用于煤体,造成煤体骨架膨胀挤压裂隙,与煤体吸附瓦斯引起的内膨胀变形相似,可采用分析瓦斯压力对煤体裂隙变形影响的方法来考虑三向应力的影响。
定义裂隙变形压缩为负、膨胀为正。 首先探讨侧向应力对如图3 所示的单裂隙煤体变形的影响,在侧向应力作用下煤体骨架向内膨胀变形引起的裂隙宽度变化量为
式中:α 为煤体骨架的内膨胀系数,α∈(0,1)。
将式(15)代入式(19),可得
另一方面,根据式(2)可以得到在法向应力作用下,裂隙的宽度与裂隙法向变形之间的关系为
式中,εn为裂隙法向应变。
侧向应力作用对裂隙变形的影响机理是否与法向应力相同,即侧向应力作用下煤体裂隙的宽度与煤体骨架的内膨胀变形是否也满足同样的关系。 在此,可假设侧向应力与法向应力两者的作用机理相同,可以得到裂隙的宽度与煤体基质内膨胀变形的关系为
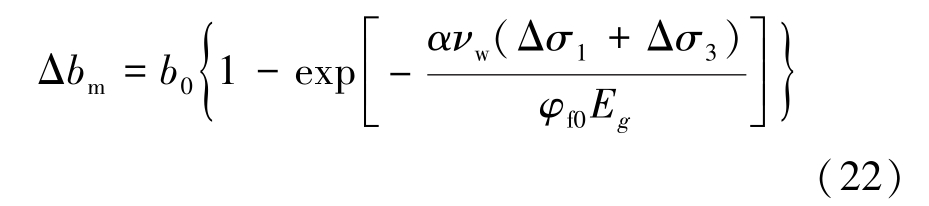
为便于比较式(20)和式(22)的区别,将式(20)中煤体骨架向内膨胀变形与裂隙变形关系命名为线性关系,将式(22)命名为指数型关系。 根据式(9)可得侧向应力作用下煤体渗透率随这2 种变形关系的表达式为
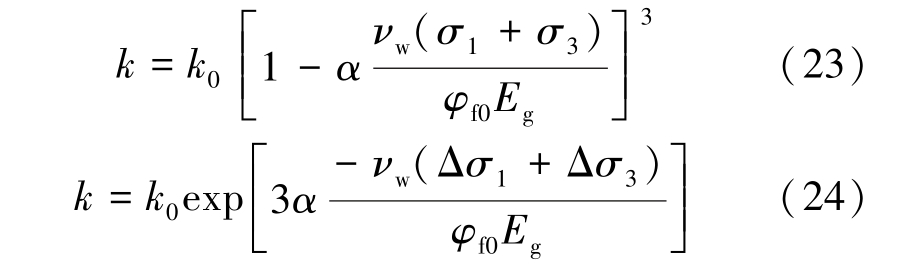
2.3 基于应力-裂隙耦合的煤体渗透率模型验证
三轴压缩渗流试验数据[26]如下:
轴压10 MPa 渗透率/10-3 μm2 0.193 931
轴压20 MPa 渗透率/10-3 μm2 0.125 842
轴压30 MPa 渗透率/10-3 μm2 0.070 472
轴压40 MPa 渗透率/10-3 μm2 0.052 854
对建立的线性关系和指数型关系进行验证,如图5 所示,可以看出,在轴压加载初期,2 种关系能较好地反映试验数据的变化,渗透率均随着轴压的增加而降低;但在轴压加载至30 MPa 后,线性关系逐渐偏离试验数据,并且随轴压的增加,偏差越来越大,这说明采用线性关系在高应力情况下会夸大轴压对裂隙变形的影响;而指数型关系在描述试验数据的变化规律上优于线性关系,能更好地描述侧向应力对裂隙变形的影响,同时也说明侧向应力对裂隙变形的作用机理与法向应力是相同的。
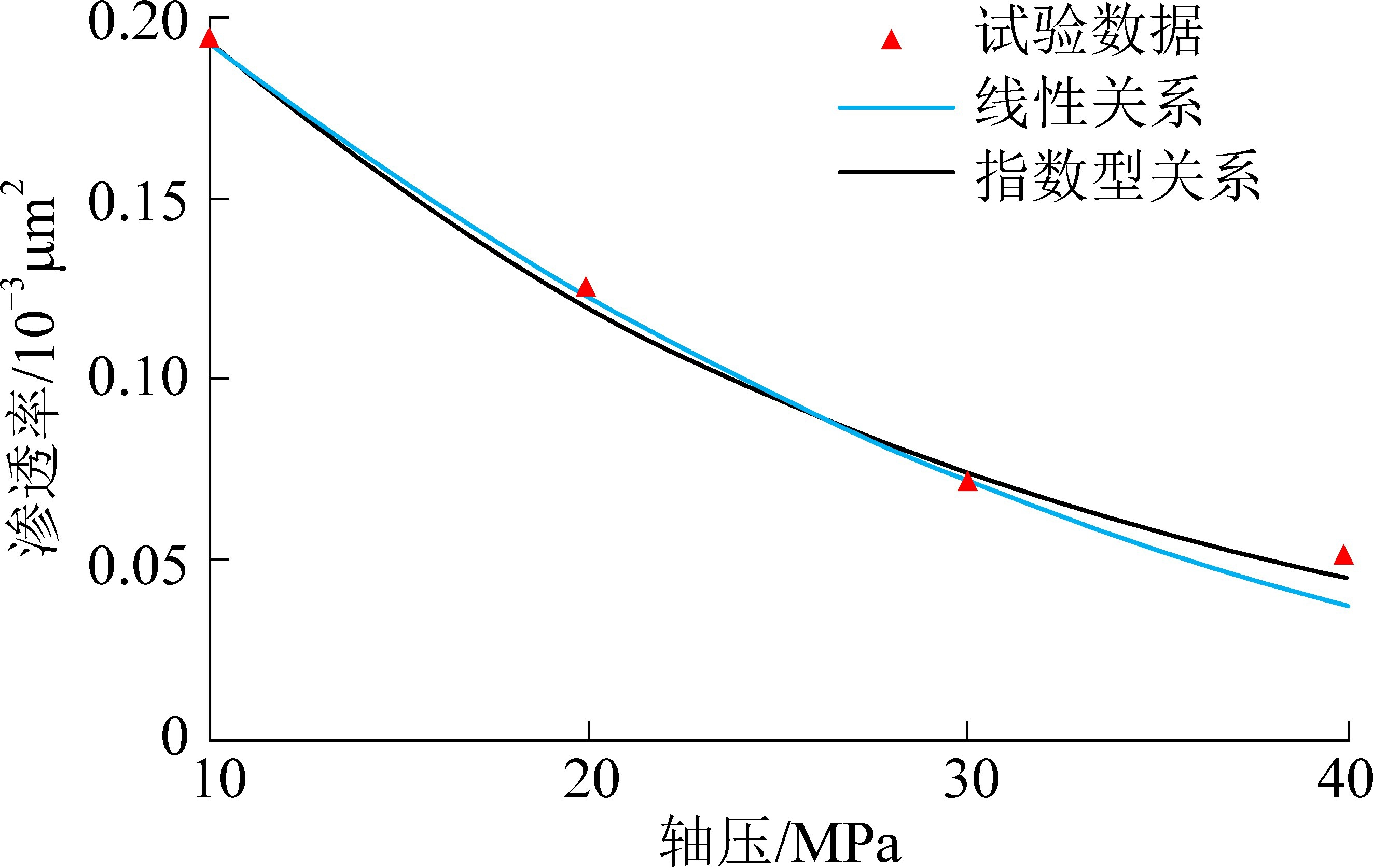
图5 线性关系和指数型关系与试验结果对比
Fig.5 Comparison of linear and exponential relationships with experimental results
在三向应力作用下,煤体裂隙的宽度受法向应力与侧向应力作用下煤体骨架内膨胀所引起的裂隙法向变形的影响,则
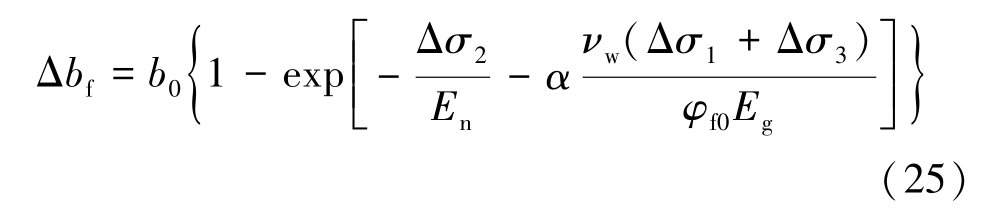
根据式(13)可得到三向应力作用下单一裂隙煤体的渗透率表达式为
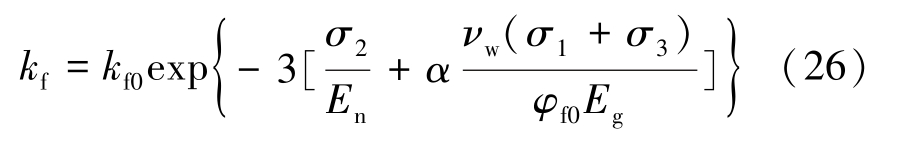
式中,kf0为初始裂隙渗透率,m2。
结合式(11),对于图1 所示的煤体任意方向的渗透率可以表示为
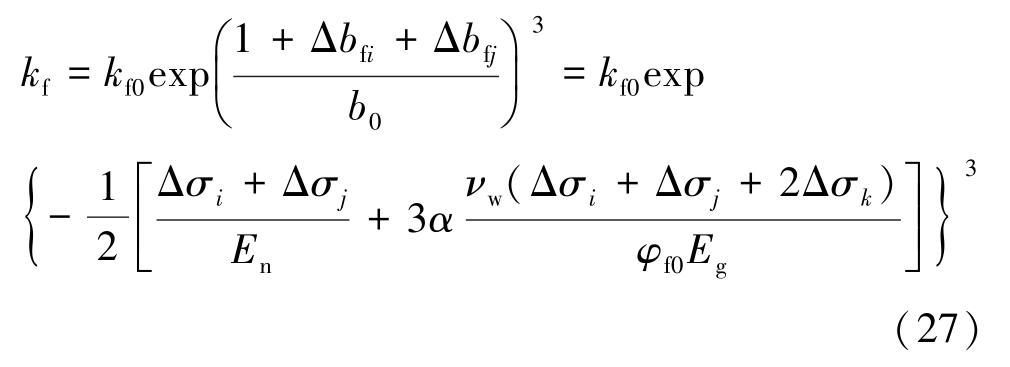
其中:Δbfi和Δbfj分别为i 和j 方向上的应力引起的裂隙宽度变化量,m;Δσi、Δσj和Δσk分别为i、 j 和k方向上主应力的变化量,MPa,其中下标i、j 和k 为3个相互正交的方向。
文献[27]基于真三轴应力-渗流耦合系统,进行了一系列三向应力和水压耦合作用下单节理花岗岩渗流试验,如图6 所示,采用其所给出的试验数据对推导的公式进行验证。 由于该试验中采用变化的水压进行渗流试验,需要考虑水压的影响,对式(27)进行修改得
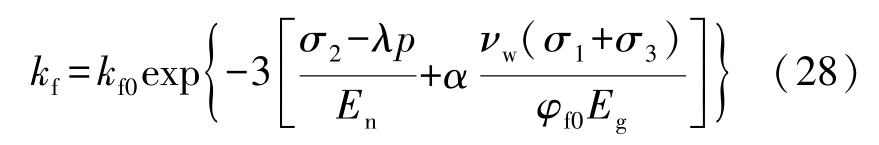
式中:λ 为biot 系数;p 为水压,MPa。
将试验数据中的水压p 和3 个方向主应力σ1、σ2、σ3及kf作为已知参数变量输入到1stOpt 软件进行全局优化非线性拟合,求得拟合公式中的未知参数。 考虑到高围压下可能会使得裂隙产生闭合而无法恢复,对渗透率的变化产生影响,在此只选择围压为3~10 MPa 的数据进行拟合,同时与采用有效应力形式的拟合表达式进行对比。 采用式(28)和有效应力计算得到拟合表达式分别为
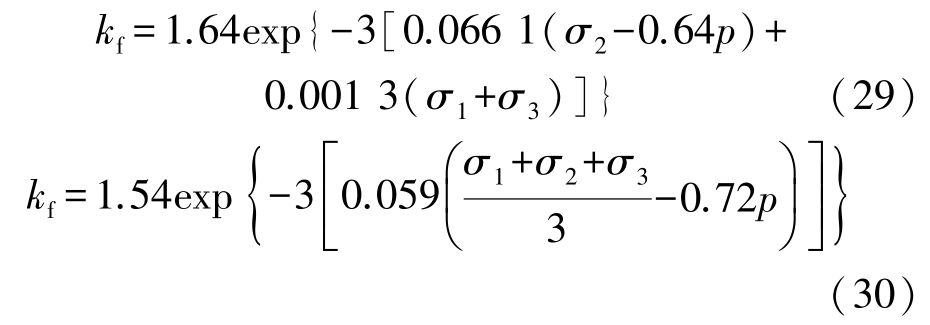
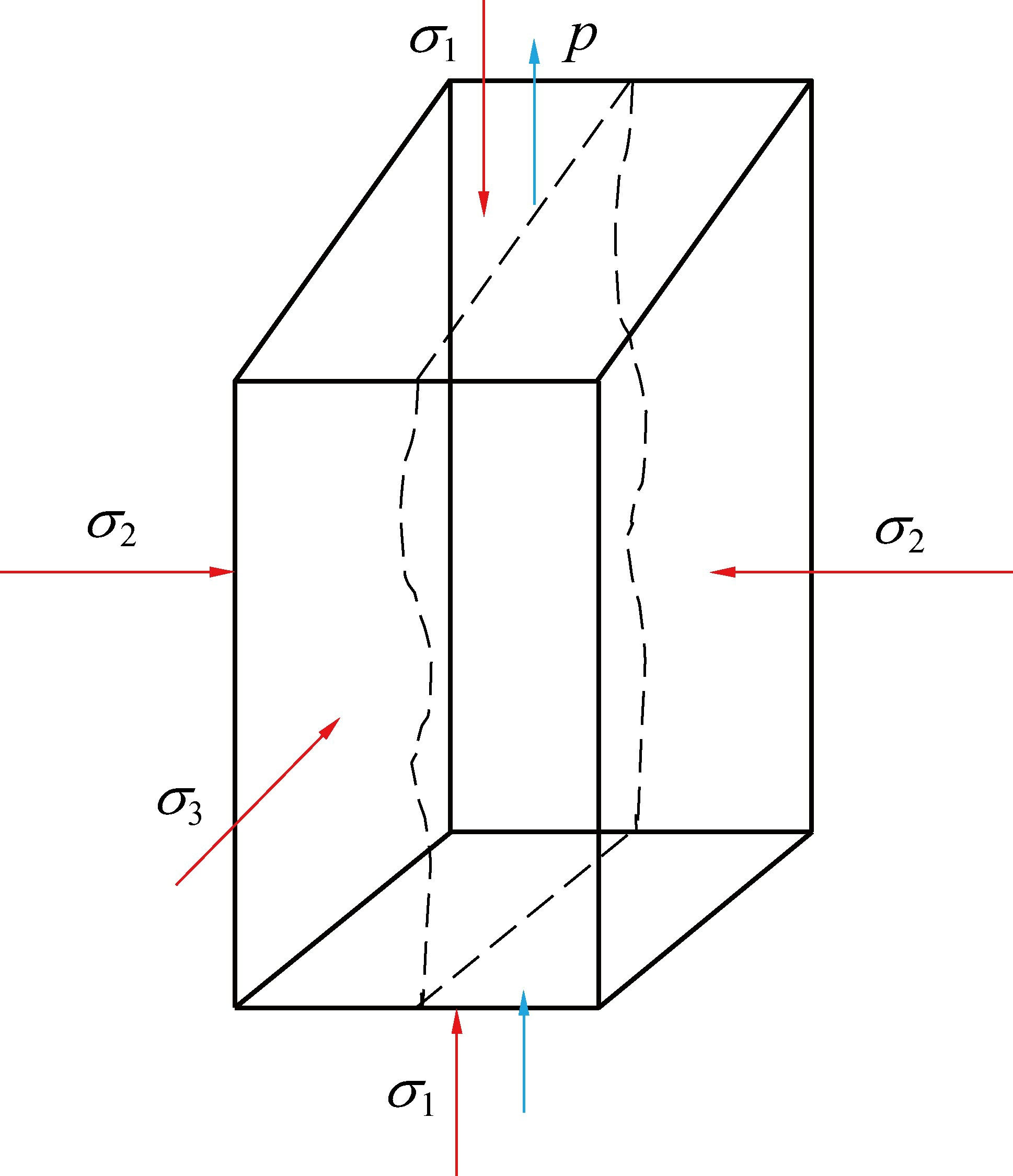
图6 三向应力和水压作用下试件受力示意[27]
Fig.6 Stress schematic of specimen under three-dimensional stress and water pressure
采用式(29)和式(30)得到的拟合值与试验值进行对比,相较有效应力公式拟合值,式(29)拟合得到的结果与试验值更加接近。 根据拟合结果,采用有效应力形式进行拟合的相关系数为0.85,而采用式(29)进行拟合的相关系数为0.97,证明式(29)在反映渗透率与三向应力和水压耦合之间的关系上是合理的。 根据上述拟合表达式, 法向应力对裂隙变形的影响系数约为侧向应力的50 倍,这说明裂隙对法向应力σ2的敏感性远大于侧向应力σ1和σ3。 由于采用有效应力将3 个应力的作用等效,扩大了侧向应力对裂隙变形的影响,不能很好反映裂隙变形对各个方向应力的敏感性,造成了计算值与试验值的偏差。
3 结 论
1)将煤体的结构简化为立方体模型,分析了瓦斯压力引起的裂隙变形与煤体基质吸附变形引起的裂隙变形对渗透率的影响,基于裂隙宽度与渗透率的关系推导了瓦斯作用下煤体的渗透率模型,并采用前人的试验数据进行了验证。
2)侧向应力对裂隙变形的影响与煤体吸附所引起的内膨胀变形相似,均通过改变煤体骨架向裂隙内部膨胀影响裂隙的变形;通过试验数据验证了侧向应力和法向应力对煤体渗透率的影响机理相同,建立了三向应力作用下煤体的渗透率模型。
3)结合前人的试验数据,进行了全局优化非线性拟合,与基于有效应力的模型相比,所建立的模型与试验数据拟合度较好,验证了所建立模型的合理性,并发现裂隙对法向应力的敏感性远大于侧向应力。
[1] 谢和平,周宏伟,薛东杰,等.我国煤与瓦斯共采:理论、技术与工程[J].煤炭学报, 2014,39(8):1391-1397.XIE Heping,ZHOU Hongwei,XUE Dongjie,et al.Theory,technology and engineering of simultaneous exploitation of coal and gas in China[J].Journal of China Coal Society,2014,39(8):1391-1397.
[2] 李波波,王 斌,杨 康,等.煤岩孔裂隙结构分形特征及渗透率模型研究[J].煤炭科学技术,http:/ /kns.cnki.net/kcms/detail/11.2402.TD.20200214.1309.006.html.LI Bobo,WANG Bin,YANG Kang,et al.Fractal characteristics and permeability model of coal hole fracture structure[J].Coal Science and Technology.http:/ /kns.cnki.net/kcms/detail/11.2402.TD.20200214.1309.006.html.
[3] 段敏克.真三轴采动影响下结构异性煤岩多场耦合响应机制及瓦斯运移规律研究[D].重庆:重庆大学,2020.
[4] DUAN Minke,JIANG Changbao,GAN Quan,et al.Experimental in⁃vestigation on the permeability,acoustic emission and energy dissi⁃pation of coal under tiered cyclic unloading[J].Journal of Natural Gas Science Engineering,2020,73:103054.
[5] DUAN Minke,JIANG Changbao,XING Huilin,et al.Study on dam⁃age of coal based on permeability and load-unload response ratio under tiered cyclic loading[J].Arabian Journal of Geosciences,2020,13(6):250.
[6] GRATY I.Reservoir engineering in coal seams:Part 1-The physical process of gas storage and movement in coal seams[J]. SPE Reservoir Engineering,1987,2(1):28-34.
[7] SHI J Q,DURUCAN S.Drawdown induced changes in permeability of coalbeds:A new interpretation of the reservoir response to primary recovery[J].Transport in Porous Media,2004,56(1):1-16.
[8] SHI J Q,DURUCAN S.A model for changes in coalbed permeability during primary and enhanced methane recovery[J].SPE Reservoir Evaluation & Engineering,2005,8(4):291-299.
[9] PALMER I,MANSOORI J.How permeability depends on stress and pore pressure in coalbeds:a new model[J].SPE Reservoir Evalua⁃tion & Engineering,1998,1(6):539-544.
[10] CUI X,BUSTIN R M.Volumetric strain associated with methane desorption and its impact on coalbed gas production from deep coal seams[J].AAPG Bulletin,2005,89(9):1181-1202.
[11] LIU J S,CHEN Z W,ELSWORTH D,et al.Evolution of coal per⁃meability from stress-controlled to displacement-controlled swell⁃ing conditions[J].Fuel,2011,90(10):2987-2997.
[12] CHEN Z W,LIU J S,ELSWORTH D,et al.Roles of coal hetero⁃geneity on evolution of coal permeability under unconstrained boundary conditions[J].Journal of Natural Gas Science and Engi⁃neering,2013,15:38-52.
[13] WANG J G,LIU J S,KABIR A.Combined effects of directional compaction,non-Darcy flow and anisotropic swelling on coal seam gas extraction[J].International Journal of Coal Geology,2013,109-110:1-14.
[14] 常宗旭,赵阳升,胡耀青,等.三维应力作用下单一裂缝渗流规律的理论与试验研究[J].岩石力学与工程学报,2004,23(4):620-624.CHANG Zongxiu,ZHAO Yangsheng,HU Yaoqing,et al.theoretic and experimental studies on seepage low of single fracture under 3D stresses[J].Chinese Journal of Rock Mechanics and Engi⁃neering,2004,23(4):620-624.
[15] LIU H H,RUTQVIST J.A new coal-permeability model:internal swelling stress and fracture-matrix interaction[J].Transport in Porous Media,2010,82(1):157-171.
[16] 臧 杰.煤渗透率改进模型及煤中气体流动三维数值模拟研究[D].北京:中国矿业大学(北京),2015.
[17] DUAN Minke,JIANG Changbao,GAN Quan,et al.Study on per⁃meability anisotropy of bedded coal under true triaxial stress and its application[J].Transport in Porous Media,2020,131(3):1007-1035.
[18] PINI R,OTTIGER S,BURLINI L,et al.Role of adsorption and swelling on thedynamics of gas injection in coal[J].Journal of Geophysical Research:Solid Earth,2009,114(B4):B04203.
[19] WANG S,ELSWORTH D,LIU J.Permeability evolution in frac⁃tured coal:the roles of fracture geometry and water-content[J].International Journal of Coal Geology,2011,87:13-25.
[20] HARPALANI S,SCHRAUFNAGEL A.Measurement of parameters impacting methane recovery from coal seams[J].International Jour⁃nal Mining Geology Engineering,1990,8:369-384.
[21] 赵阳升,杨 栋,郑少河,等.三维应力作用下岩石裂缝水渗流物性规律的实验研究[J].中国科学E 辑:技术科学,1999,29(1):82-86.ZHAO Yangsheng, YANG Dong, ZHEN Shaohe, et al.Experimental study on physical properties of water seepage in rock fracture under three-dimensional stress[J].Chinese Science E:Technical Science,1999,29(1):82-86.
[22] 刘才华,陈从新.三轴应力作用下岩石单裂隙的渗流特性[J].自然科学进展,2007,17(7):989-994.LIU Caihua,CHEN Congxin.Seepage characteristics of single rock fracture under triaxial stress[J].Advances in Natural Science,2007,17(7):989-994.
[23] 张金才,王建学.岩体应力与渗流的耦合及其工程应用[J].岩石力学与工程学报,2006,25(10):1981-1989.ZHANG Jincai,WANG Jianxue.Coupled behavior of stress and permeability and its engineering applications[J].Chinese Journal of Rock Mechanics and Engineering,2006,25(10):1981-1989.
[24] ZHANG J,STANDIFIRD WB,ROEGIER JC,et al.Stress-de⁃pendent fluid flow and permeability in fractured media:From lab experiments to engineering applications[J].Rock Mechanics and Rock Engineering,2007,40(1):3-21.
[25] 孔 洋,朱珍德,阮怀宁.三向应力作用下节理岩体渗流-应力耦合特性[J].岩土力学,2018,39(6):2008-2016.KONG Yang,ZHU Zhende,YUAN Huaining.Stress-seepage cou⁃pling characteristics of jointed rock mass under three principal stresses[J].Rock and Soil Mechanics,2018,39(6):2008-2016.
[26] 李 波.受载含瓦斯煤渗流特性及其应用研究[D].北京:中国矿业大学(北京),2013.
[27] 尹立明,郭惟嘉,陈军涛.岩石应力-渗流耦合真三轴试验系统的研制与应用[J].岩石力学与工程学报,2014,33(S1):2820-2826.YIN Liming,GUO Weijia,CHEN Juntao.Development of true tri⁃axial rock test system of coupled stres-seepage and its application[J].Chinese Journal of Rock Mechanics and Engineering,2014,33(S1):2820-2826.
