0 引 言
螺旋钻机作为一种可以高效安全地回采露天矿最终境界下端帮压煤的矿山机械,已经在德国和澳大利亚有着广泛且成功的应用[1]。螺旋钻机运用螺旋钻杆开采出1排或多排的水平钻孔,从端帮的邻空面回采压煤且无需支护,适用于使用单一的露天或井工开采方法难以回采或者经济效益不理想的情况。目前国内学者对螺旋钻机开采端帮煤炭的研究多集中在对多层螺旋钻孔的采场稳定性研究,且研究方法大多为利用数值模拟软件分析比较不同方案中参数的合理性。曾钱帮等[2]运用数值模拟的方法,研究了螺旋钻机不同的钻孔开采顺序对采场稳定性的影响。研究表明:层间不同开采顺序对煤柱稳定性影响较大,而同层内的钻孔开挖顺序对煤柱稳定性影响不明显;黄侃等[3]运用数值模拟方法对螺旋钻机开采下不同水平孔间煤柱宽度及垂向隔层的不同排布方式对采场稳定性的影响进行了研究。研究表明:由于采场间垂向隔层为煤柱提供了侧向应力,所以在煤柱优化设计时需要考虑采场间的垂向隔层厚度;程国明等[4-5]对特厚煤层条件下采用螺旋钻机开采细长窄煤柱时,煤柱的破坏过程进行了数值模拟。研究表明:螺旋钻机开采所引起的煤柱内应力分布以及破坏方式与条带式分布不同。
鉴于以往鲜有对单层螺旋钻孔参数设计的研究,且未兼顾压力拱这一采场中的“小结构”对围岩内应力分布状态、关键层以及永久隔离煤柱内应力集中程度的影响。笔者以矿山实例为背景对单层螺旋钻孔设计参数进行研究,基于压力拱理论分析数值模拟结果,选出最优开采方案,希望为螺旋钻机开采边坡煤设计方案提供依据。
1 钻孔周围应力分布特征
螺旋钻机开采单层钻孔与条带开采在开采形式上相近,都可以简单概括为采出一个条带后留设一个条带,如此往复。留设的条带煤柱能承载上覆岩层的载荷,保证地表移动和变形的均匀且可控。2种开采方式在开采过程中,相邻采空区间煤柱内应力变化曲线有如下相同点:①在未进行开采时,煤体受上覆岩层均布荷载作用;②当煤柱一侧开采结束后,煤柱一定范围内形成支承压力带及局部塑性区;③煤柱两侧均开采结束后,若煤柱能保持稳定状态,则煤柱所受垂直应力呈马鞍型分布,煤柱两侧存在一定宽度的塑性破坏区,煤柱中出现弹性核区;④在周围其他采硐开采的影响作用下,煤柱两侧塑性破坏区逐渐扩展,弹性核区中心应力达到煤柱极限强度,核区应力变化曲线进入平台期,此时是煤柱失稳破坏的临界状态,若弹性核区中心应力稍有上升煤柱将迅速失稳[6]。突变理论可以指导条带煤柱的参数设计[7-8],即建立支承煤柱的尖点突变方案,导出极限状态下非弹性区在煤柱中的占比,判定煤柱宽度是否合理。基于以上相同点,突变理论也适用于螺旋钻机回采露天矿端帮压煤的煤柱参数设计,但需要确定一种定义相邻钻孔间煤柱有效宽度的方法。不同于矩形断面硐室,圆形钻孔内最大切向应力发生在孔的两帮中点和顶底的中部。钻孔上形成的压力拱将拱顶上方压力传递至两侧拱脚处,由于围岩在发生破坏时首先沿着压力拱塌落,而钻孔拱顶本身就接近最佳硐形,所以钻孔周围煤岩破坏主要发生在钻孔两侧,参数设计时无需考虑钻孔拱顶破坏问题。
2 开采关键参数
2.1 相邻钻孔间煤柱宽度
2.1.1 孔间煤柱有效宽度
规则煤柱的有效宽度容易确定,但对于相邻圆形钻孔间这种不规则煤柱的有效宽度笔者提出一种方法:相邻螺旋钻孔间煤柱可以看作无梁楼盖设计中上下端带有斜柱帽的房柱。无梁楼盖是一种建筑结构,其特点为无主梁和次梁的板柱结构体系。柱帽具有实际作用:较宽的斜柱帽能减小顶板柱帽及跨中位置处的弯矩[9],房柱对顶板中弯矩的影响主要来自斜柱帽,中柱则负责承担载荷,这与钻孔周围的应力分布规律相吻合。由于煤柱强度随煤柱最大内切圆直径的增加而增强[10-11],所以对于相邻钻孔间煤柱,其有效宽度应为中柱最大内切圆直径。如图1所示,其中a为煤柱的有效宽度(简称为孔间煤柱宽度)。
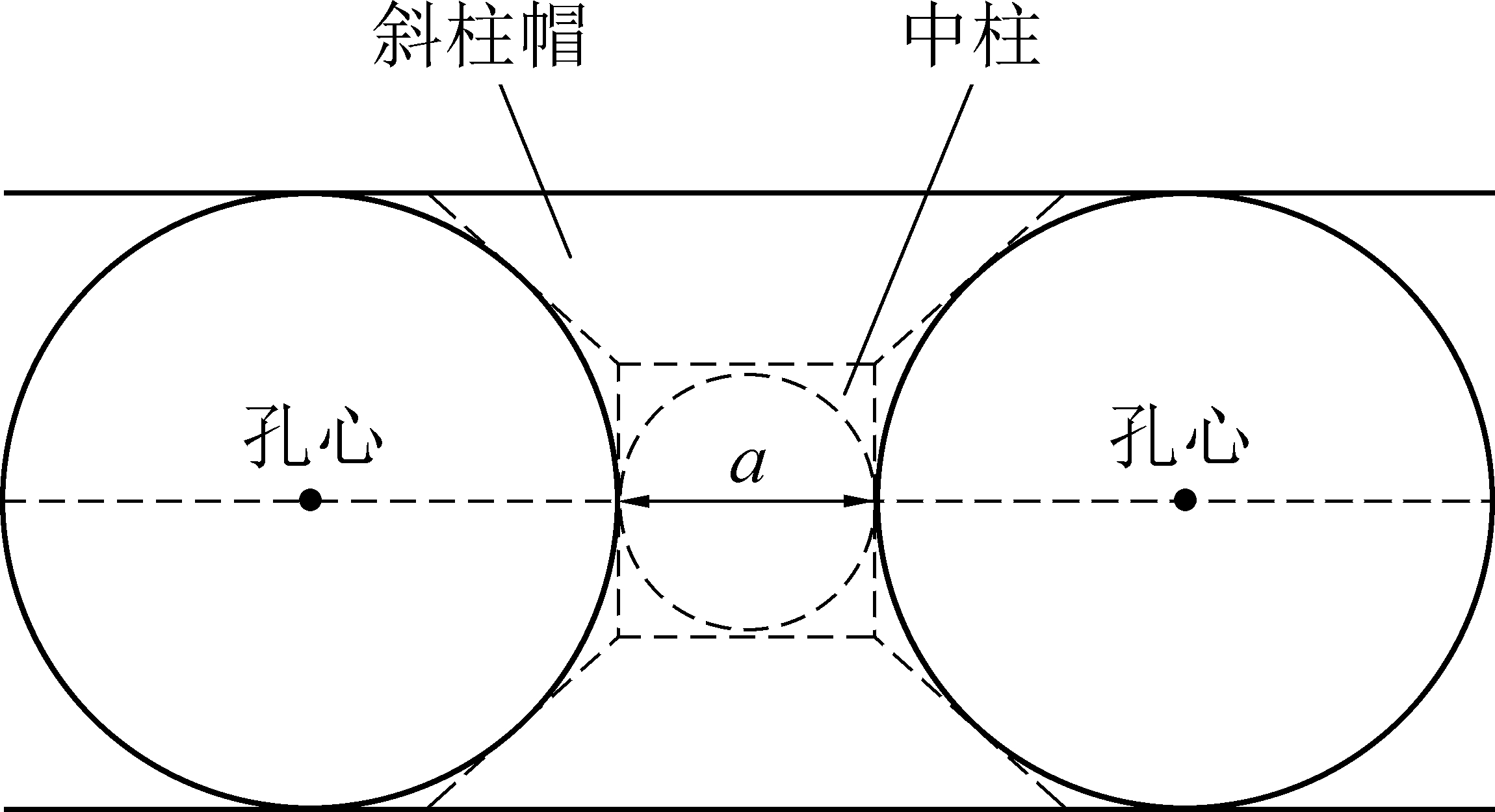
图1 相邻钻孔间煤柱有效宽度
Fig.1 Effective width of pillar between adjacent boreholes
2.1.2 采场稳定性判定标准
王东等[7]基于尖点突变理论得到了突变分叉集方程:
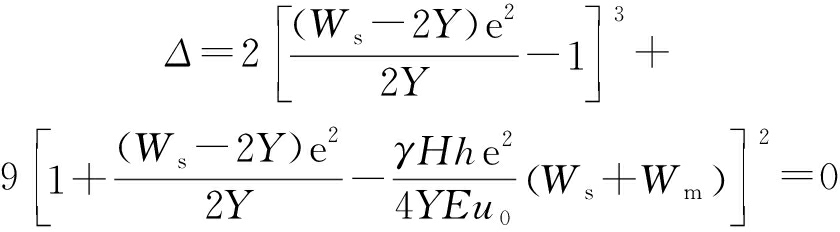
(1)
式中:Δ为系统分叉集控制方程;Ws为煤柱宽度;Wm为采硐宽度;Y为煤柱屈服区宽度;E为煤柱的弹性模量;H为上覆岩层的平均厚度;γ为容重;h为煤层厚度;u0为峰值载荷下煤柱的变形。
式(1)表明:当Δ<0时,系统会发生突变,即支承煤柱屈服区宽度2Y与煤柱宽度Ws之比大于0.88时,煤柱将发生突变失稳。根据有效支承区域理论,即煤柱支承着自身上部和间隔相邻煤柱平分的上覆岩层重力[12]。孟达等[13]对房柱式开采采场稳定性进行了相似材料模拟试验并得出结论:当采场中间煤柱失稳垮落瞬间,相邻煤柱所承载的有效支承区域载荷增加1倍,每次垮落都导致基本顶承载的载荷成倍增加,而且相邻煤柱由破坏前的轴心受压转化为偏心受压,逐步从小偏心受压到大偏心受压,从而导致基本顶连续破坏,产生连锁反应,最终导致整体切冒。所以确保采场中点处煤柱的稳定是保障钻孔群及边坡稳定的重要前提。选取采场中点处煤柱为监测煤柱(若采场中孔间煤柱数量为奇数,则选取中点处煤柱;若采场中孔间煤柱数量为偶数,则选取中点处2根煤柱),以监测煤柱中屈服区宽度与煤柱有效宽度的比值是否大于0.88为判定采场稳定性的标准。
2.2 钻孔数量
ANWAR[14]研究认为当相邻隧道间距较小时,2个隧道上方形成1个压力拱;当间距较大时,各自形成独立的压力拱,如图2所示。随着相邻采空区数量的增多,原本各自独立的压力拱形成1个大压力拱,拱脚前移,拱顶高度增加,围岩内应力集中程度增加。当应力集中程度大于顶板岩层的承载能力,上覆岩层沿压力拱轮廓发生破坏。同时,根据岩层控制的关键层理论[15],主关键层对直至地表的岩层活动起控制作用。所以同一水平上相邻钻孔数量不能过多。
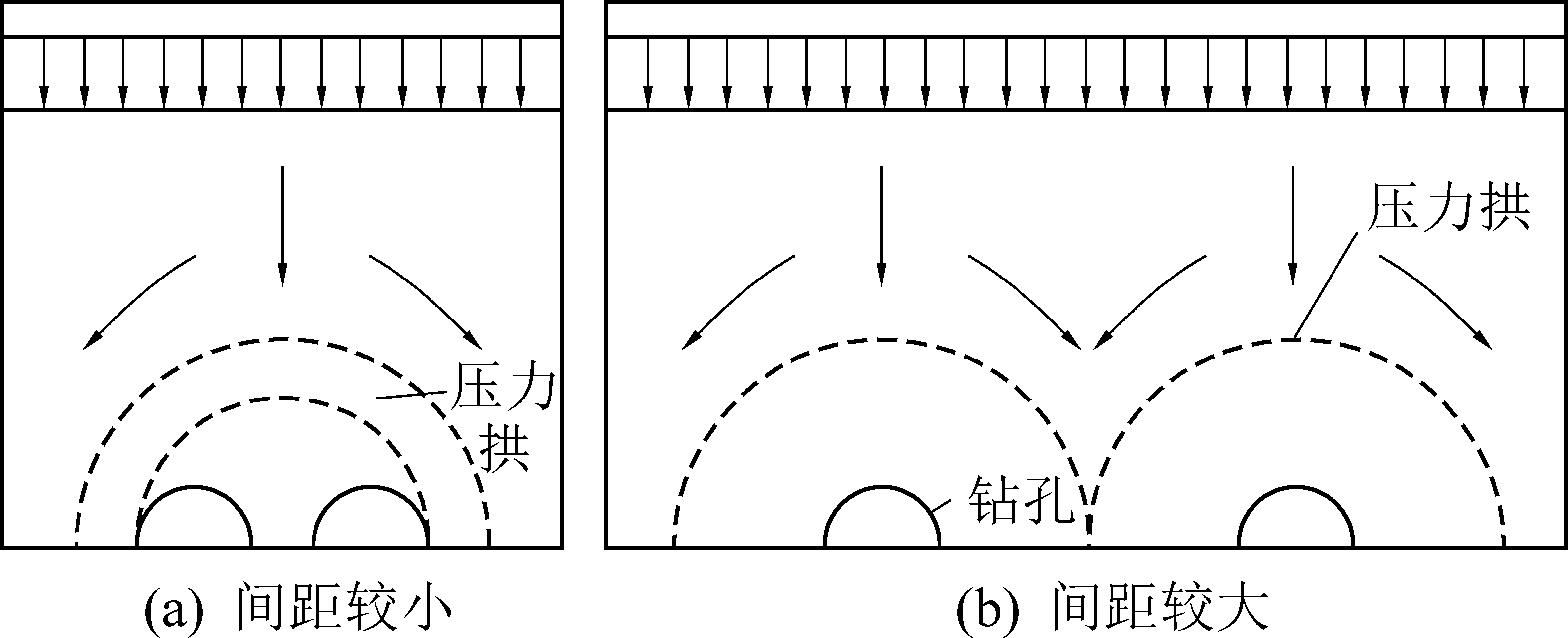
图2 相邻隧道压力拱
Fig.2 Adjacent tunnel pressure arch
2.3 永久隔离煤柱宽度
螺旋钻机开采边坡煤钻孔排布参数可以看作多孔之间相互影响问题。孔周边的应力集中系数K可以表示为
K=σ′/σ
(2)
其中:σ′为孔间煤柱内部应力峰值;σ为原岩应力。应力集中系数一方面随着D与B之比增大而增大(D为孔径,B为孔周边的间距),另一方面又受同一水平上孔的数量影响。显然,孔的数量越多,孔周边的应力集中系数越大[15]。
而合理宽度的永久隔离煤柱可以有效地减小相邻钻孔群之间的相互影响。当钻孔上独立的压力拱形成一个更大的压力拱时,永久隔离煤柱实际上为压力拱的拱脚处,拱脚处的应力状态受压力拱传递的不稳定载荷的集中程度影响。在埋深、钻孔直径不变的情况下,钻孔数量愈多、相邻钻孔间煤柱宽度愈小,拱脚处的应力集中系数愈大。隔离煤柱增加了相邻钻孔群间距,有效地分隔了相邻工作面垮落空间的横向贯通和纵向扩展,隔开了相邻工作面上覆岩层沉降曲线[16]。定义孔周边应力集中系数K在永久隔离煤柱中点处等于1时,永久隔离煤柱宽度为最优值。
3 钻孔排布数值模拟
3.1 工程概况
某露天矿开采后,在边坡下有大量的压煤,应用其他采煤方法很难将这部分煤采出,故采用螺旋钻机将部分压煤采出。煤层坡面角60°,南北走向倾角较小,可认为是近水平煤层。边坡上覆岩层最小厚度20 m,最大厚度130 m。煤层平均厚度5 m,顶板为粉砂岩、细砂岩,底板以泥岩为主,煤层全区发育,煤层结构简单。螺旋钻机对端帮煤层露头进行单水平顺序钻孔回采,钻头最大直径1.2 m,钻孔与钻孔之间留设隔离煤柱,采出一系列钻孔后留设一段永久隔离煤柱。
压力拱高度与关键层高度有如下关系:压力拱发育至关键层后若关键层破断则基于破断位置重新起拱,若不破断则拱顶位于关键层附近[17]。所以,同一水平相邻钻孔数量应保证在压力拱发育至关键层后,拱内围岩应力集中小于顶板围岩的承载能力,避免拱内围岩破坏导致关键层下围岩离层引起关键层破断。
3.2 正交试验
“正交设计法”是研究与处理多因素试验的一种科学的试验方法。经分析选取相邻钻孔间煤柱宽度、相邻钻孔数量、永久隔离煤柱宽度为3个主要因素,每个因素取3个水平,共设置9次数值模拟试验,绘制L9(34)正交表(表1)。钻孔埋深为固定值,不作为正交试验中的因素,试验方案见表2。
表1 单层钻孔排布各因素水平
Table 1 Single layer drilling arrangement of each factor level
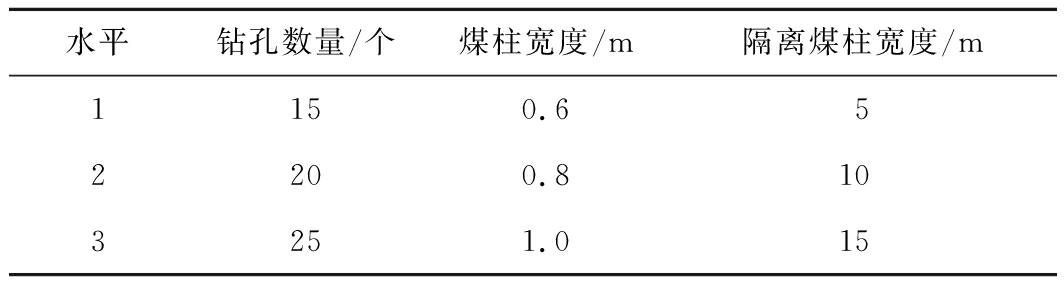
水平钻孔数量/个煤柱宽度/m隔离煤柱宽度/m1150.652200.8103251.015
表2 试验方案
Table 2 Experimental scheme
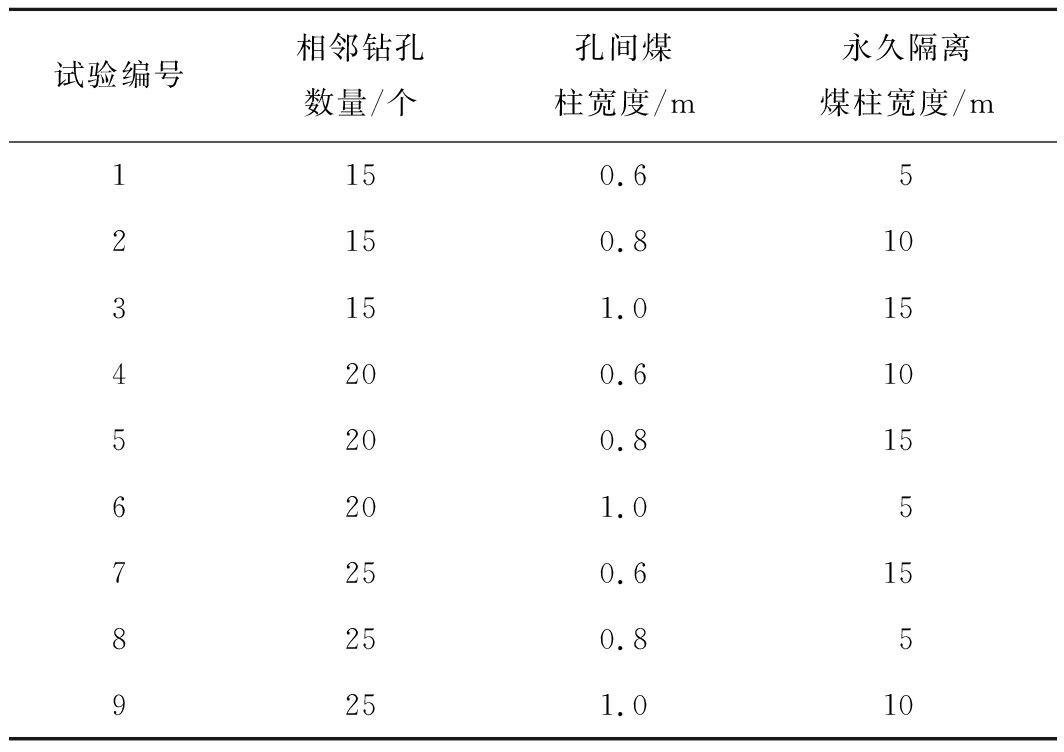
试验编号相邻钻孔数量/个孔间煤柱宽度/m永久隔离煤柱宽度/m1150.652150.8103151.0154200.6105200.8156201.057250.6158250.859251.010
3.3 钻孔模型建立
数值模拟计算主要借助有限差分软件。考虑到钻孔长度可达60 m,并可能进一步增加,且在数值计算的过程中常把该问题视为平面问题求解,所以在数值模拟的过程中将模型简化为三维切片。计算应用摩尔-库仑弹塑性模型,结合采场的实际情况,模型位置选取距钻孔底部1 m处厚度1 m的切片。根据圣维南原理,局部效应的影响可以由足够大的围岩范围消除,取模型高度为煤层厚度的6~7倍。最终模型的尺寸为:120 m×1 m×98 m,共1 623 400个单元。左右和下边界施加位移约束,上边界没有施加约束。模型与应力监测路径如图3所示。

图3 数值模拟模型及应力监测路径
Fig.3 Numerical simulation model and stress monitoring path
3.4 力学参数
通过对取自采场的煤岩样进行单轴抗压、抗拉强度试验以及单轴压缩变形试验并经胡克布朗准则折减后获得了模拟所需要的采矿岩石力学参数,见表3。
表3 煤岩样物理力学试验结果
Table 3 Results of coal physical and mechanical test
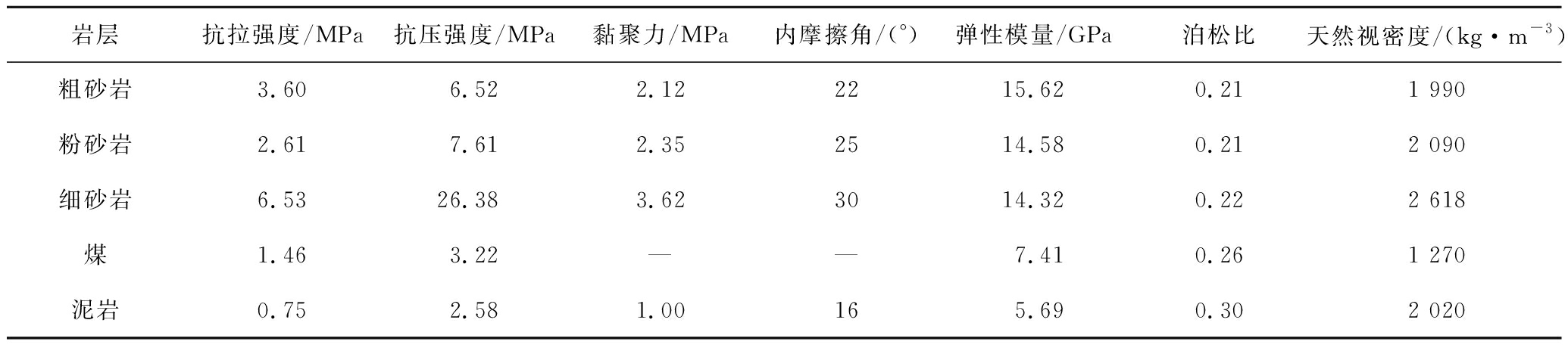
岩层抗拉强度/MPa抗压强度/MPa黏聚力/MPa内摩擦角/(°)弹性模量/GPa泊松比天然视密度/(kg·m-3)粗砂岩3.606.522.122215.620.211 990粉砂岩2.617.612.352514.580.212 090细砂岩6.5326.383.623014.320.222 618煤1.463.22——7.410.261 270泥岩0.752.581.00165.690.302 020
4 钻孔排布模拟结果
由于模拟结果数据较多,无法详尽列出,仅选取9组方案中拱顶路径上的原岩应力与开挖后水平方向和垂直方向应力变化曲线,如图4、图5所示,拱腰路径上应力集中系数见表4。
表4 拱腰路径上应力集中系数
Table 4 Coefficient of stress concentration on arch waist path
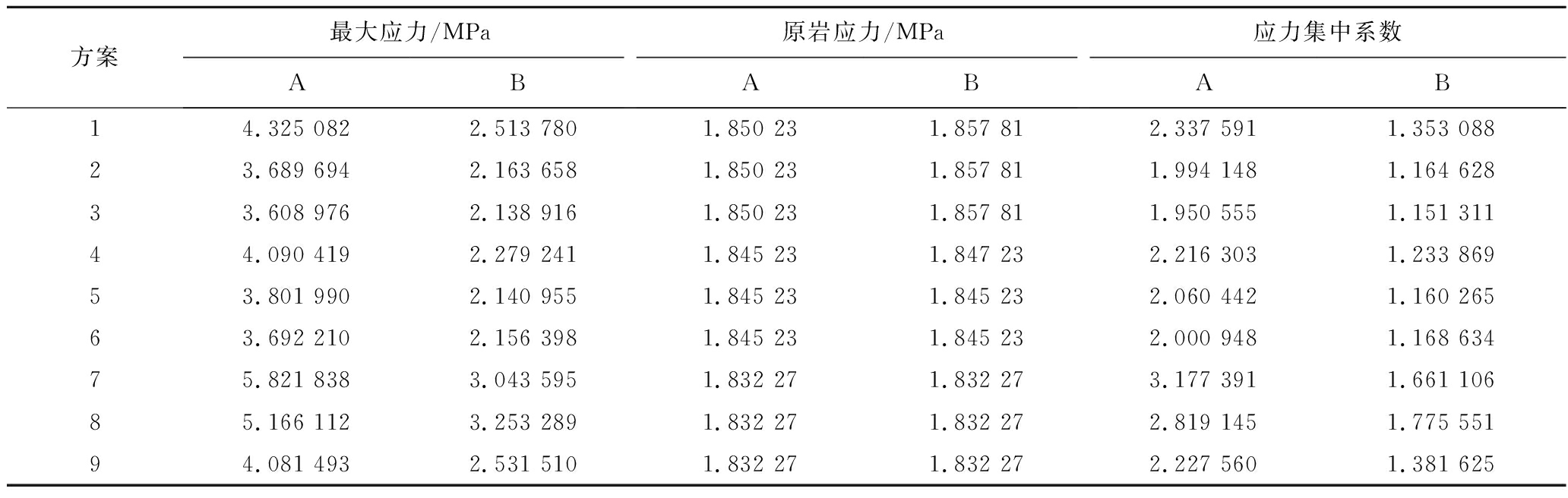
方案最大应力/MPa原岩应力/MPa应力集中系数ABABAB14.325 0822.513 7801.850 231.857 812.337 5911.353 08823.689 6942.163 6581.850 231.857 811.994 1481.164 62833.608 9762.138 9161.850 231.857 811.950 5551.151 31144.090 4192.279 2411.845 231.847 232.216 3031.233 86953.801 9902.140 9551.845 231.845 232.060 4421.160 26563.692 2102.156 3981.845 231.845 232.000 9481.168 63475.821 8383.043 5951.832 271.832 273.177 3911.661 10685.166 1123.253 2891.832 271.832 272.819 1451.775 55194.081 4932.531 5101.832 271.832 272.227 5601.381 625
注:A为模型两侧拱腰路径;B为模型中点拱腰路径。
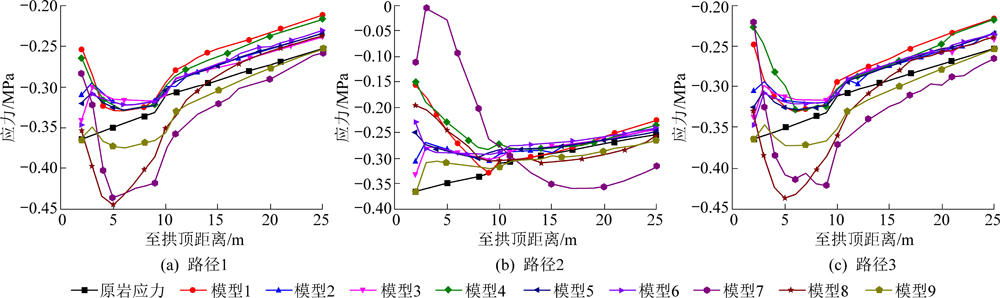
图4 拱顶路径1、2、3上水平应力变化
Fig.4 Horizontal stress variation on vault paths 1,2 and 3
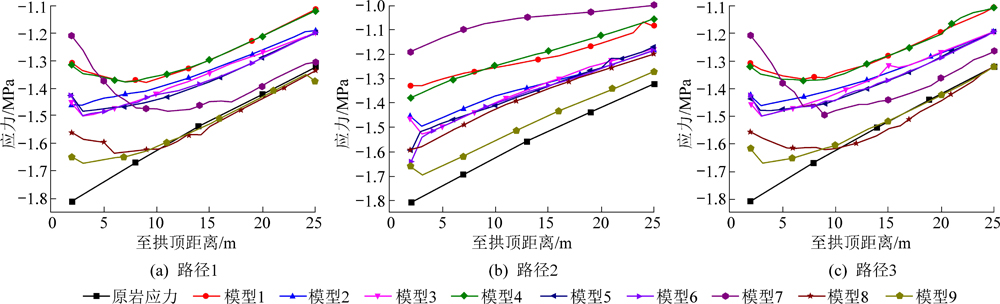
图5 拱顶路径1、2、3上垂直应力变化
Fig.5 Vertical stress variation on vault path 1,2 and 3
随着开采进程的推进,钻孔开采对拱顶监测路径上应力的影响主要反映在:路径1、路径3上原本随埋深增加而增加的水平应力与竖直应力,即拱顶监测路径上的切向应力和径向应力均出现拐点。具体现象为:拱顶监测路径1、路径3上,钻孔周围的切向应力在开挖后沿拱顶监测路径方向先增大,出现切向应力压紧区,后下降并回归至原岩应力水平;沿拱顶监测路径方向,径向应力先增大后减小,在各条拱顶监测路径上,除方案8、方案9外,方案1—方案7中径向应力始终低于原岩应力水平,说明围岩中出现松动区域。
拱腰应力监测路径上的应力集中系数表明,保持钻孔数量不变,孔间煤柱宽度的增加会降低拱脚处的应力集中程度;保持孔间煤柱宽度不变,相邻钻孔数量的增加会提高拱脚处应力集中程度;永久隔离煤柱能有效地减小拱脚处应力集中程度和相邻钻孔群之间的影响。
5 数值模拟结果分析
1)对于拱顶内边界和外边界的确定主要选取如下2个准则:①根据切向应力判定准则,将切向应力σxx由最大值减小到原岩应力水平的点作为压力拱的外边界。该准则反映出钻孔的开挖对周围煤岩的影响范围。②根据拱体内部主应力极值判定准则:钻孔开挖后切向应力由低于原岩应力增加到最大值后又逐渐恢复到原岩应力水平,将切向应力增加到最大值的点作为压力拱的内边界。
由图5可知,在拱顶应力监测路径2上,除方案7外,剩余8组方案中的切向应力均在距钻孔拱顶9 m处增加到最大值,在14 m处由最大值回归至原岩应力水平,即压力拱内边界高度9 m,外边界高度14 m;而方案7中切向应力最大值位于距钻孔拱顶18 m处,距钻孔拱顶25 m处仍未回归至原岩应力水平。在监测路径1和路径3上,方案1—方案6中切向应力在7 m处增加到最大值,在9 m处回归至原岩应力水平,即方案1—方案6压力拱内边界高度7 m,外边界高度9 m;方案8、方案9中切向应力距钻孔拱顶6 m处达到最大值,在14 m附近回归至原岩应力水平,即压力拱内边界6 m,外边界14 m。压力拱将上覆岩体载荷转化为拱的切向应力,并将其传递至两侧永久隔离煤柱,保证回采作业处于应力降低区。根据采场中岩层赋存条件,距钻孔拱顶9~25 m处的粗砂岩层符合关键层标准。除方案7外的所有方案中压力拱外边界均位于关键层附近。由图5可知,在监测路径1和路径3上,仅有方案8、方案9中径向应力在关键层附近回归至原岩应力水平,表明未出现松动区。在监测路径2上,方案9中径向应力与原岩应力差值最小,可知方案9中关键层附近松动区域最小,关键层附近围岩较稳定。
2)9组方案的塑性区分布如图6所示,由于有限差分软件具有动态松弛特性,只有处于平衡状态的单元才有意义,所以将shear-p设为空单元。方案1、方案4、方案7中监测煤柱内塑性区宽度与煤柱的有效宽度比值为93%~100%,远大于临界值88%,表明煤柱内塑性区已贯通,将发生突变失稳。方案2、方案5、方案8中监测煤柱内塑性区宽度与其有效支承宽度比值为55%~60%,未达到临界值,煤柱保持稳定。方案3、方案6、方案9中监测煤柱两帮处存在小范围剪切破裂区,塑性区宽度与煤柱有效宽度比值为36%~40%,远小于临界值,煤柱保持稳定。
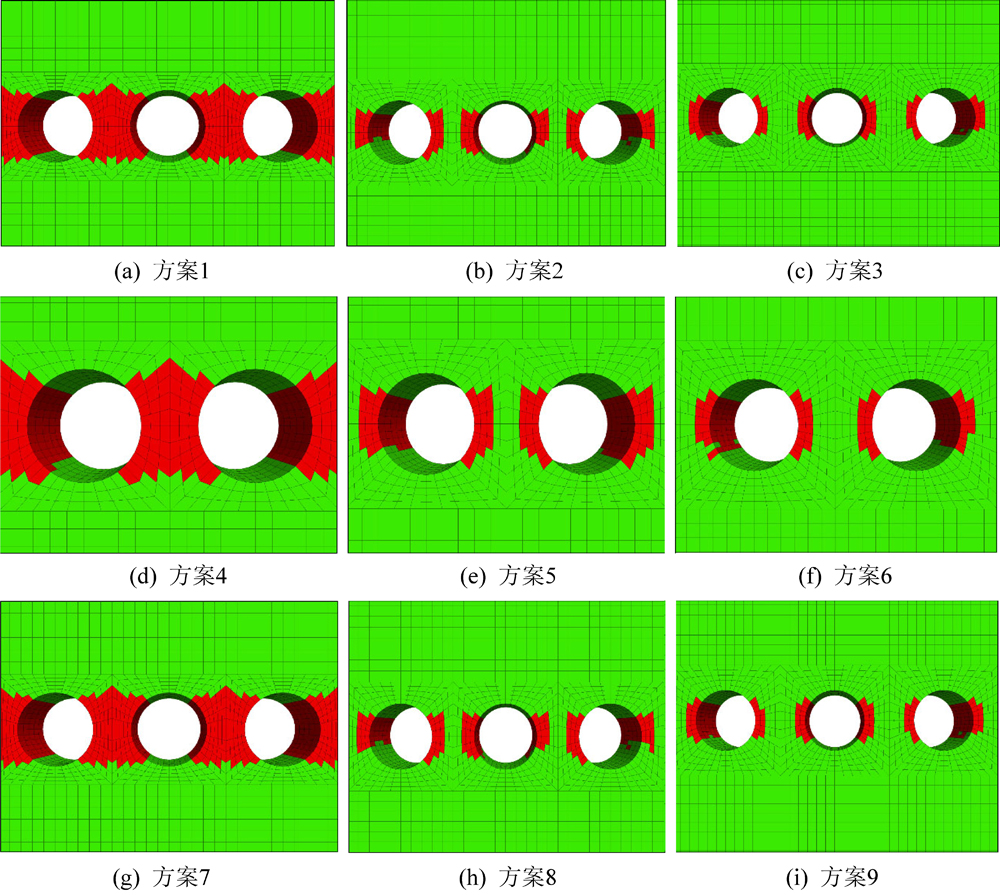
图6 各方案监测煤柱内塑性区分布
Fig.6 Monitor plastic zone in coal pillar
3)对于拱腰处的应力监测路径,径向应力σ′zz=σxx,切向应力σ′xx=σzz。拱腰路径上的压力拱内边界同样适合内部主应力极值确定准则,但不对其进行研究。拱腰路径上压力拱的外边界可以用该路径上的切向应力集中系数确定开挖对周围煤岩内应力大小的影响范围,故选取拱腰路径上切向应力集中系数等于1处为拱腰路径上压力拱的外边界。
由表4可知,在钻孔直径不变的情况下,孔间煤柱宽度的减小和钻孔数量的增加都会使拱脚应力集中系数增大。在拱腰应力监测路径上,切向应力自钻孔群两侧至永久隔离煤柱中点方向先增大后减小,但始终大于原岩应力,说明在拱腰路径上未出现松动区域。除方案7、方案8外,剩余方案中沿拱腰应力监测路径上的切向应力在永久隔离煤柱中点处基本回归至原岩应力水平,表明这7组方案中的永久隔离煤柱能有效地消除相邻钻孔的影响。
6 结 论
1)将压力拱理论、正交试验法与数值模拟相结合,基于压力拱理论分析正交试验所得方案在开采后的数值模拟结果,优选出合理单层钻孔排布方案,从而使参数设计更科学,降低开采作业风险。
2)结合建筑学中无梁楼盖设计理论,提出一种定义相邻圆形钻孔间煤柱有效宽度的方法,即将煤柱分解成由斜柱帽与中柱组成的房柱,该方法适合螺旋钻机开采钻孔参数设计研究。
3)经分析,不同的钻孔排布参数对开采后围岩内的应力分布有不同程度的影响;相邻钻孔数量25个,相邻钻孔间煤柱宽度1 m,永久隔离煤柱宽度10 m,关键层附近松动区域最小、监测煤柱稳定、永久隔离煤柱宽度合理,优于其他方案。但缺少实际开挖所得数据,未对最优方案的合理性进行科学验证。
[1] SCHMID M,KNISSEL W. Highwall mining of coal(part 1):foundation and state of the art of mining systems[J].Surface Mining,2001,53(1):53-62.
[2] 曾钱帮,程国明,刘环宇.到界边坡下螺旋钻机开采顺序对煤柱稳定性的影响研究[J].岩土工程学报,2005,27(7):769-771.
ZENG Qianbang,CHENG Guoming,LIU Huanyu. Study on influence of excavation sequence on the stability of coal pillar under final highwall with auger mining[J].Chinese Journal of Geotechnical Engineering,2005,27(7):769-771.
[3] 黄 侃,程国明.露天矿高边坡钻孔采矿法的参数研究[J].煤炭学报,2004,29(2):164-166.
HUANG Kan,CHENG Guoming.Study on the parameters of highwall auger mining in open pit mine[J]. Journal of China Coal Society,2004,29(2):164-166.
[4] 程国明,黄 侃,王思敬,等.细长窄煤柱破坏机理的数值分析[J].岩土力学,2004,25(2):266-269.
CHENG Guoming,HUANG Kan,WANG Sijing,et al. Numerical simulation of failure mechanism of slender coal pillars[J]. Rock and Soil Mechanics,2004,25(2):266-269.
[5] 程国明,黄 侃,王思敬,等.螺旋钻机开采的力学效应及煤柱稳定性研究[J].岩石力学与工程学报,2004,23(9):1460-1464.
CHENG Guoming,HUANG Kan,WANG Sijing,et al. Study on mechanical effect and coal pillar stability during highwall mining with auger machine[J]. Chinese Journal of Rock Mechanics and Engineering,2004,23(9):1460-1464.
[6] 吴立新,王金庄. 建(构)筑物下压煤条带开采理论与实践[M]. 徐州:中国矿业大学出版社,1994:32-98.
[7] 王 东,姜聚宇,韩新平,等.褐煤露天矿端帮开采边坡支承煤柱稳定性研究[J].中国安全科学学报,2017,27(12):62-67.
WANG Dong,JIANG Juyu,HAN Xinping,et al.Stability of supporting coal pillar for slope highwall mined in lignite surface min[J].China Safty Science Journal,2017,27(12):62-67.
[8] 郭文兵,邓喀中,邹友峰.条带煤柱的突变破坏失稳理论研究[J].中国矿业大学学报,2005,34(1):77-81.
GUO Wenbing,DENG Kazhong,ZOU Youfeng. Study on failure and instability of strip coal pillar by catastrophic theory [J]. Journal of China University of Mining & Technology,2005,34(1):77-81.
[9] 王 迪,杨小平,郑月昱,等.柱帽对无梁地铁车站结构顶板的影响分析[J].建筑结构,2018,48(S1):697-703.
WANG Di,YANG Xiaoping,DENG Yueyu,et al. Analysis of column cap's influence on roof slab of column-free metro station [J].Building Structure,2018,48(S1):697-703.
[10] 彭小沾,崔希民,王家臣,等.基于Voronoi图的不规则煤柱稳定性分析[J].煤炭学报,2008,33(9):966-970.
PENG Xiaozhan,CUI Ximin,WANG Jiachen,et al.Stability analysis of irregular coal pillars based on Voronoi diagram[J].Journal of China Coal Society,2008,33(9):966-970.
[11] CUI Ximin,GAO Yongge,YUAN Debao.Sudden surface collapse disasters caused by shallow partial mining in Datong coalfield,China[J].Natural Hazards,2014,74(2):911-929.
[12] 陈彦龙,吴豪帅.露天矿端帮开采下的支承煤柱突变失稳机理研究[J].中国矿业大学学报,2016,45(5):859-865.
CHEN Yanlong,WU Haoshuai.Catastrophe instability mechanism of rib pillar in open-pit highwall mining[J].Journal of China University of Mining & Technology,2016,45(5):859-865.
[13] 孟 达,王家臣,王进学.房柱式开采上覆岩层破坏与垮落机理[J].煤炭学报,2007,32(6):577-580.
MENG Da,WANG Jiachen,WANG Jinxue. Mechanism on the failure and caving of roof strata in pillar and house mining[J]. Journal of China Coal Society,2007,32(6):577-580.
[14] ANWAR K A. Study on stress rock arch development around dual caverns[D].Nanyang:Technological University,2003.
[15] 钱鸣高,石平五,许家林.矿山压力与岩层控制[M].徐州:中国矿业大学出版社,2010.
[16] 师修昌.浅部隔离煤柱对覆岩运移的控制及其合理留设[J].重庆大学学报,2019,42(10):106-114.
SHI Xiuchang.Control of overlying strata migration by shallow isolated coal pillars and their reasonable setting-up[J].Journal of Chongqing University,2019,42(10):106-114.
[17] 杨达明,郭文兵,于秋鸽.浅埋近水平煤层采场覆岩压力拱结构特性及演化机制分析[J].采矿与安全工程学报,2019,14(2):323-330.
YANG Daming,GUO Wenbing,YU Qiuge.Structural characteris-tics and evolution mechanism of overlying strata pressure arch in shallow and flat seams[J].Journal of Mining & Safety Engineering,2019,14(2):323-330.
