0 引 言
煤粒瓦斯扩散规律对煤与瓦斯共采具有重要意义。一方面可以用来估算煤层瓦斯资源的可采性,即评价煤层瓦斯的运移难度;另一方面,在计算瓦斯含量值时,可用于推算取样过程中的损失瓦斯量,即可提高瓦斯资源总量评价的精确度[1-3]。关于煤粒瓦斯扩散规律国内外研究主要集中在影响因素、模型建立、机理描述和应用实践等方面。其中,在对煤粒内瓦斯的解吸扩散特性进行数学描述时,常以达到吸附平衡态作为前提,在设定外部压力为常数的条件下解出合理的解析解[1]。1975年英国学者CRANK J对提出了定压边界下的单孔扩散模型[4]。基于此,文献[5-6]给出了更适合工程应用的简化单孔扩散模型。之后,单孔模型及其简化模型在工程中得到了大量推广和应用,亦被大量应用于描述试验中瓦斯吸附或解吸的动力学规律[7-9]。
一般而言,煤体扩散试验有吸附扩散试验和解吸扩散试验2种。吸附扩散试验常在密闭空间中进行,以给定合适的初始压力,观察压力降低规律,转而根据气体状态方程来分析瓦斯吸附量随时间的变化情况[10]。此种情形可看为是瓦斯在受限空间中的扩散行为,为定容边界。而解吸扩散试验则常常在开放空间中进行,将解吸罐连接特制的解吸量筒或者流量计来确定不同时刻的瓦斯解吸量[11],此种情形为非受限空间的定压边界。两者所形成的吸附或解吸动力学规律在形态上是相似的,但边界条件却是存在差异的。单孔扩散模型的初衷是用于描述煤粒在恒压解吸条件下的扩散规律[1]。部分文献直接将之用于描述吸附扩散现象,有所欠妥[12-13]。因此,比较吸附扩散过程中2种模型的拟合差异,并对比获得的扩散系数大小,可以对扩散试验设计产生指导作用。另外,在工程应用中,相较于小尺度的煤粒,在描述大尺度的煤体中瓦斯吸附解吸规律时,由定压边界和定容边界得到的2种扩散系数哪个更为科学,也值得探究。
1 试验方法
1.1 样品选取
试验选取山西焦煤集团双柳矿区3号煤层煤样,将块状煤体用粉碎机磨碎,筛分出0.074~0.200 mm粒径煤样10 g用于工业分析,0.20~0.25 mm粒径煤样20 g用于等温吸附试验,1~3 mm粒径煤样约50 g用于吸附试验。
1.2 煤样工业分析
依据国际标准ISO 17246:2010《煤的工业分析》,使用5E-MAG6600工业分析仪对样品工业成分进行测定,煤样组分分析结果见表1。
表1 煤样基本信息
Table 1 Basic information of coal sample
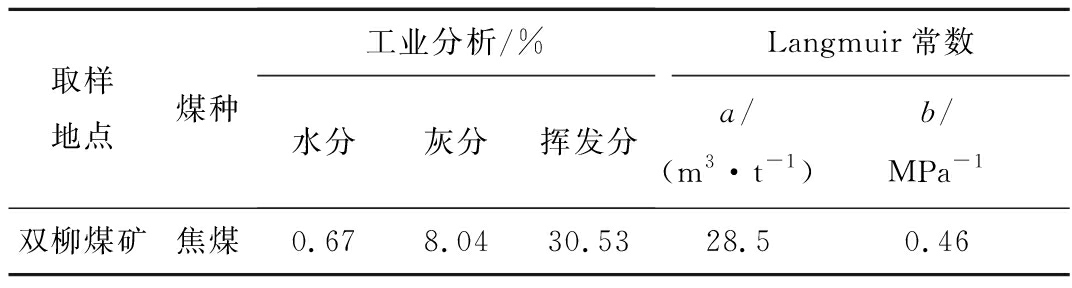
取样地点煤种工业分析/%水分灰分挥发分Langmuir常数a/(m3·t-1)b/MPa-1双柳煤矿焦煤0.678.0430.5328.50.46
1.3 等温吸附试验
等温条件下,煤对瓦斯的吸附符合单分子动力学吸附方程Langmuir方程,即:
L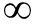
![]()
(1)
式中:L∞为平衡压力为P时的极限吸附量,mL/g;a为吸附常数,表示可燃基的极限吸附瓦斯量,mL/g;b为吸附常数,反映其吸附能的大小,MPa-1;P为瓦斯吸附平衡压力,MPa;A、W分别为煤中的灰分和水分,%。
上述等温吸附方程给出了瓦斯吸附量和平衡压力的关系。测定时,需依据国家标准MT/T 752—1997《煤的甲烷吸附量测定方法(高压容量法)》,对样品进行等温吸附试验,得到煤样的瓦斯吸附常数a值和b值,见表1。
1.4 吸附扩散试验
首先将试筛选好的1~3 mm颗粒煤装入清洁的煤样罐中,并在煤粒上部放入适量的棉花,以防止煤粒在脱气过程中堵塞管路。之后将煤样罐放入60 ℃恒温水浴中进行真空脱气。脱气真空度降至4 Pa后,将煤样罐转移至30 ℃恒温水浴中,待温度平衡后向煤样罐中迅速充入纯度99.9%以上的CH4,分别充至3、4、5 MPa后关闭阀门,然后放入吸附30 ℃恒温水浴中进行吸附平衡试验。间隔一定时间读取煤样罐压力表示数,初期测点应尽量密集,后期可适度加大读点间隔,直至压力表示数不变,即煤样达到吸附平衡状态为止,如图1所示。

图1 试验装置及过程
Fig.1 Experimental device and process
2 试验结果与分析
2.1 受限空间内瓦斯压力降低规律
在不同时间对进行吸附平衡过程中的瓦斯压力进行监测,如图2所示。从图2可以发现,不同初始压力条件下,煤样经过不同时间才能达到压力上的平衡态,且压力降低呈现初期快速,后期慢速的对数函数形式。初始压力为3、4和5 MPa条件下的平衡压力分别为2.36、3.30和3.90 MPa。另外,平衡时间随着初始压力增大而呈增加趋势,初始压力5 MPa的曲线大约在120 h 后才完成平衡。究其原因,主要是由于双柳煤样特殊的半开孔孔隙结构引起[14-15]。
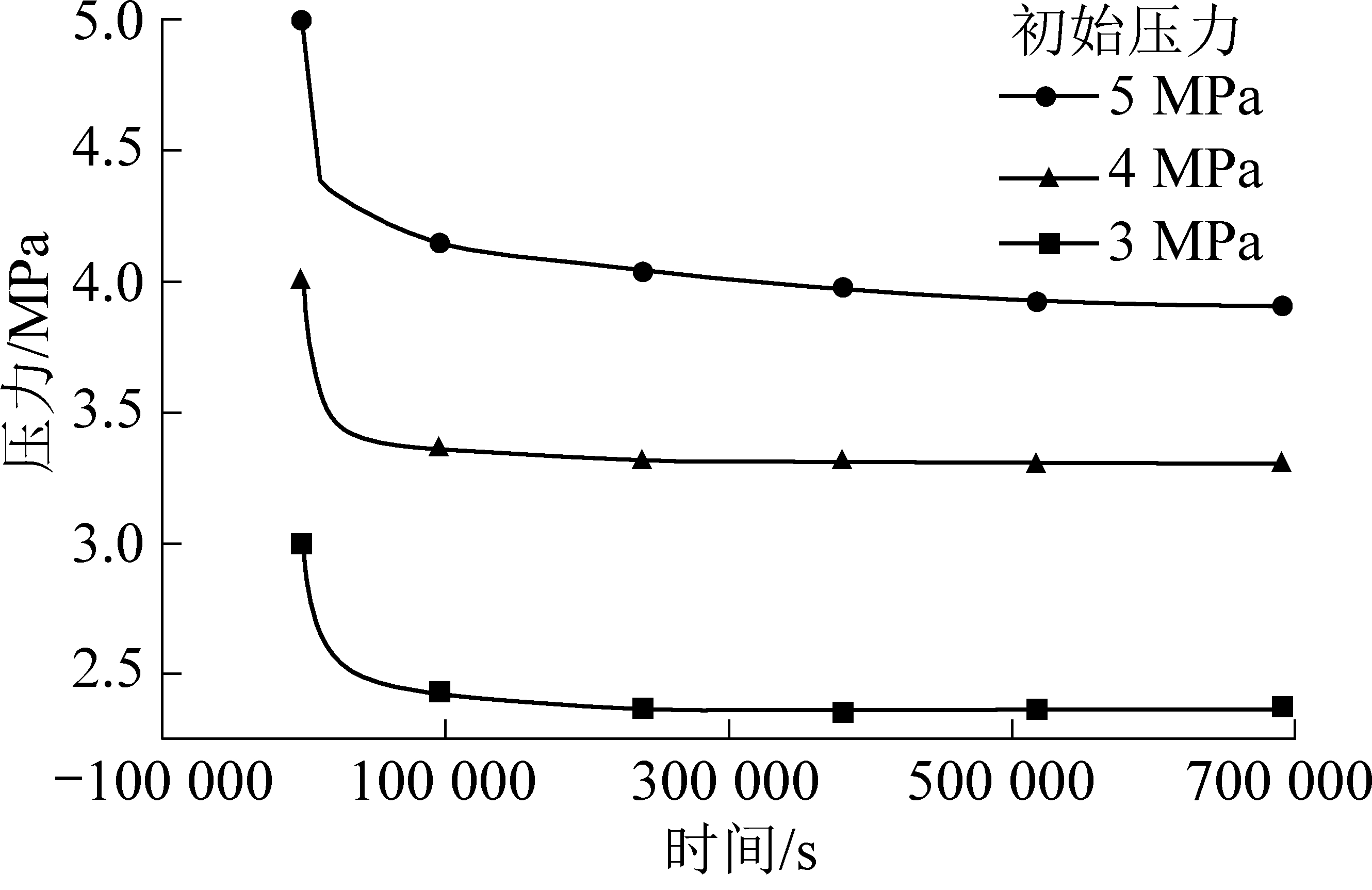
图2 瓦斯压力降低曲线
Fig.2 Attenuation curve of gas pressure
多孔吸附剂的吸附可以分为3个基本过程:①吸附质分子在吸附剂表面的薄液层中扩散;②吸附质分子在吸附剂粒子内扩散;③吸附质分子吸附在吸附剂粒子表面[16]。对于物理吸附体系而言,第3种过程的速度急快,可以忽略不计。所以在时间尺度上,瓦斯在煤中的吸附解吸过程可近似看做瓦斯在多孔介质中的扩散过程。不同的孔隙结构,所产生的孔壁作用势不同,瓦斯分子表现出的扩散特性也就不同,如图3所示。微孔内孔壁之间距离很近,孔壁产生的作用势重叠,对吸附质分子的作用力比小孔、中孔和大孔要大,瓦斯分子很容易凝聚成微乳状液滴,吸附扩散速度非常小[10]。而对于开放性孔,孔口两端均有瓦斯分子扩散进入,比只有一端进入的半开放性孔达到吸附饱和的时间更短。吸附初期,煤粒孔隙表面与内部存在较大的瓦斯浓度差Δc,同时煤粒外层大孔和中孔较多,产生的壁面势较小,扩散驱动力较大,瓦斯分子可以在孔隙内自由扩散,短时间内压降较大;随之瓦斯分子大量进入微孔中,煤粒表面压力降低,Δc逐步减小,而且孔壁作用势较大,瓦斯分子被壁面势能捕获后难以逃逸,其只能通过表面迁移来进行扩散,扩散难度越来越大,扩散速度也会越来越慢[17-18]。
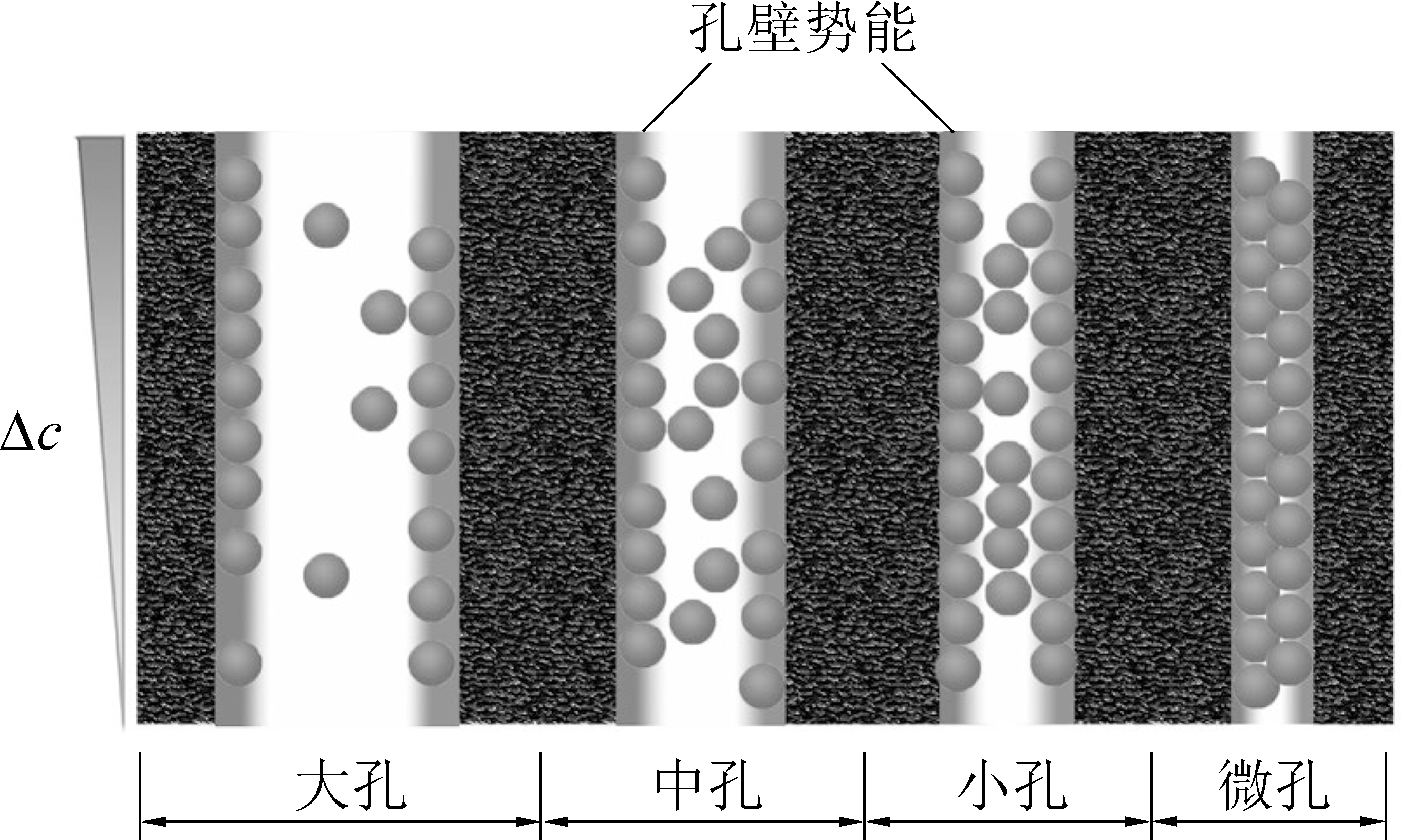
图3 不同孔隙中瓦斯分子的吸附扩散
Fig.3 Adsorption diffusion in pores of coal particles
2.2 受限空间内瓦斯吸附动力学规律
利用真实气体状态方程,可以将压降的数值,转换为煤粒的吸附量。由于试验在恒温水浴中进行,吸附过程中温度不变,由真实气体状态方程PV=znRT,可以推导出:
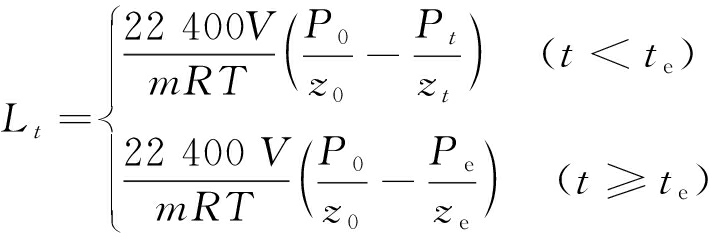
(2)
式中:Lt为t时刻的吸附量,mL/g;P0、Pe、Pt分别为初始时刻、吸附平衡时刻以及t时刻的瓦斯压力,MPa;Z0、Ze、Zt分别为初始时刻、吸附平衡时刻以及t时刻的压缩系数;te为达到吸附平衡状态时所用的时间,min;V为解吸罐来被煤粒占用的体积,mL;m为煤样的质量,g;T为气体温度,K;R为普适气体常数,J/(mol·K)。
式(2)确定了不同吸附时间下煤粒的瓦斯吸附量,如图4所示。与压降曲线特征相似,其瓦斯吸附量在初期上升很快,但增长速率逐渐降低,在平衡时,初始压力为3、4和5 MPa的吸附量分别为7.97、8.72和13.73 mL/g。
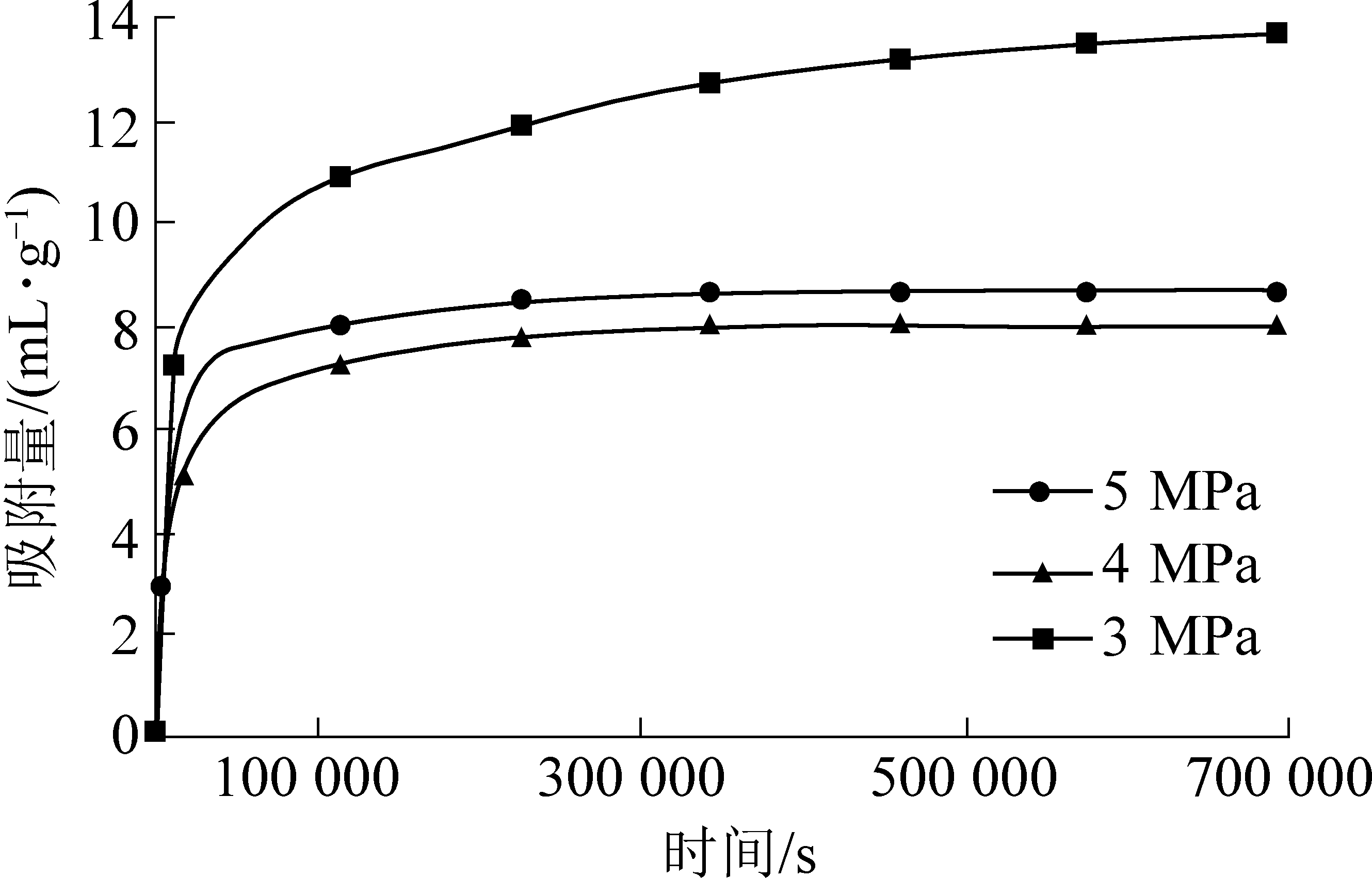
图4 瓦斯吸附扩散曲线
Fig.4 Gas adsorption/diffusion curves
2.3 定压和定容扩散模型适配差异
瓦斯在煤中运移速度的快慢常用扩散系数来表征。对于吸附扩散而言,文献中常用的扩散模型有恒定压力条件的扩散模型和恒定体积条件的扩散模型2种。
1)恒定压力条件。恒定压力条件下,煤粒表面浓度保持为零。其符合常规解吸试实验的边界条件,因而常被用来拟合解吸扩散系数,为狭义上的单孔扩散模型[1]。因其形式相对于定容条件更为简单,故而文献中也有部分学者以此来拟合瓦斯吸附扩散的过程,但从定义上来讲,有所欠妥。
(3)
式中:Mt、M∞分别为t时刻的吸附量和极限吸附量,mL/g;D为表观扩散系数,m2/s;r为扩散距离,m。
2)恒定体积条件。恒定容积条件则要求吸附的空间是限定的,此时相当于表面浓度是随时间变化的。这种边界条件相对于定压环境来说,更为复杂,所以使用的人较少。CRANK[4]曾给出定容条件下三维球形扩散的解析解为
(4)
式中,qn为下述方程的非零根。
(5)
(6)
式中:V为未被煤粒占用的体积,mL;Vc为煤粒的体积,mL;α为都被煤粒占用所体积与煤粒体积之比。
定压和定容条件的模型实际上均为单孔均质假设,亦可称之为广义上的单孔模型。利用式(3)和式(4)分别对3条吸附曲线进行拟合,可以得到不同条件拟合出的扩散系数,如图5所示。

图5 不同扩散模型的拟合差异
Fig.5 Fitting discrepancy of different diffusion models
从图5中可知,对于吸附扩散试验而言,定容条件扩散模型较之定压条件扩散模型拟合效果更好,而这种优势在吸附初期更为明显。图6以初始压力为3 MPa为例,给出了2种模型对试试验数据在吸附初期放大后的拟合情况对比。定容扩散模型由于其与更符合吸附扩散试试验故而拟合效果更好。
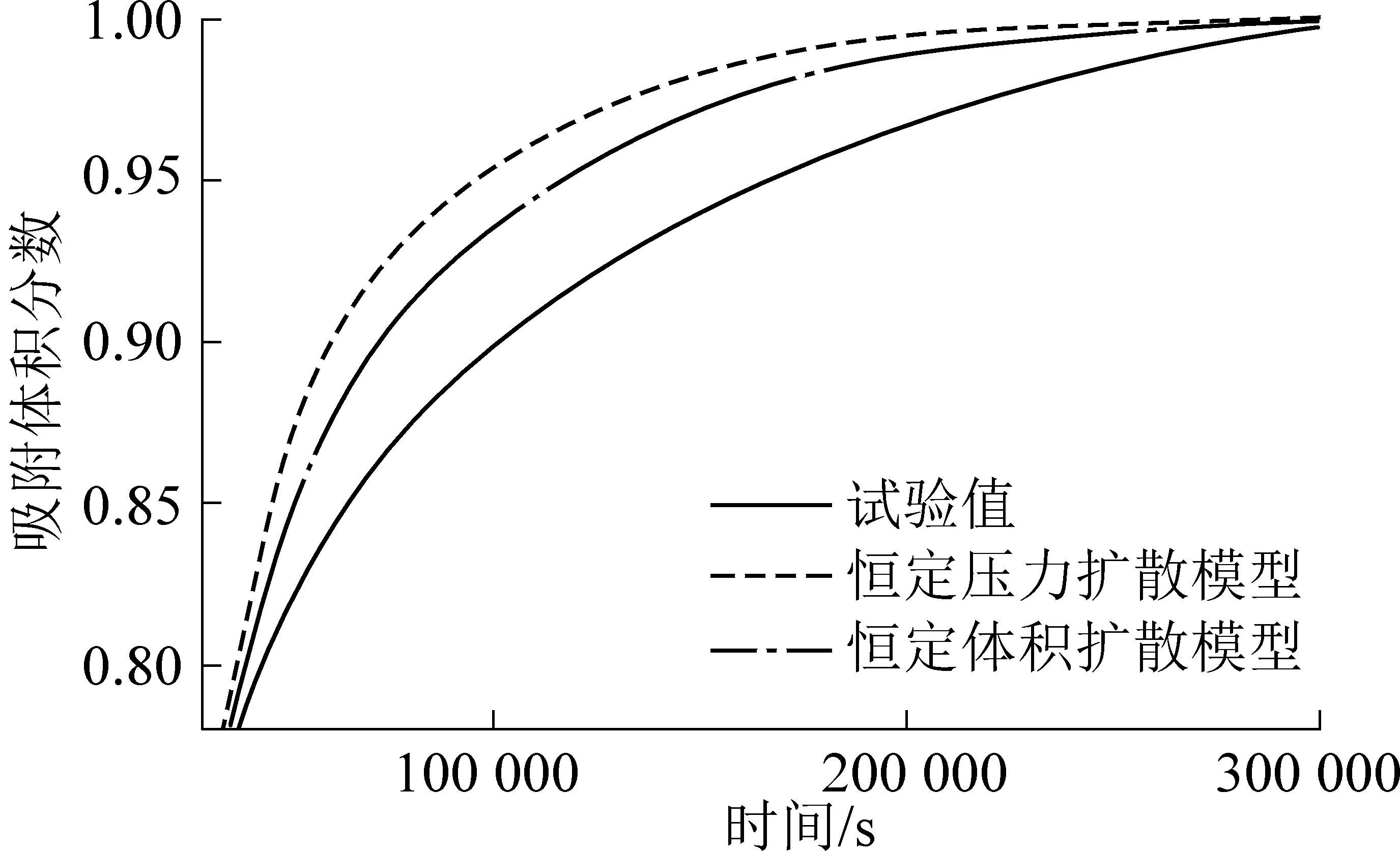
图6 不同扩散模型初期拟合效果对比
Fig.6 Comparison of fitting performance of different diffusion models
另外,2种模型除拟合度上的差异外,拟合得出的扩散系数也存在差异,如图7所示。由于扩散距离r在试验中不可测[19],因此常用有效扩散系数D/r2来体现扩散特性的差异。定压、定容扩散模型拟合得出的有效扩散系数分别为:3.29×10-6 s-1和1.88×10-6 s-1(3 MPa);3.00×10-6 s-1和1.60×10-6 s-1(4 MPa);2.48×10-6 s-1和1.28×10-6 s-1(5 MPa)。两者的比值分别为1.75、1.88和1.94倍,且随着压力的升高而逐渐加大。这表明用定压模型测得的扩散系数较之真正的定容扩散系数要大2倍左右。究其原因,主要是恒定压力的边界给了瓦斯分子一个容易逸散的空间,相较于浓度逐渐升高的定容边界来说,扩散难度更小,扩散系数更大。因此,直接采用定压扩散模型直接去拟合吸附扩散系数是有偏差的。
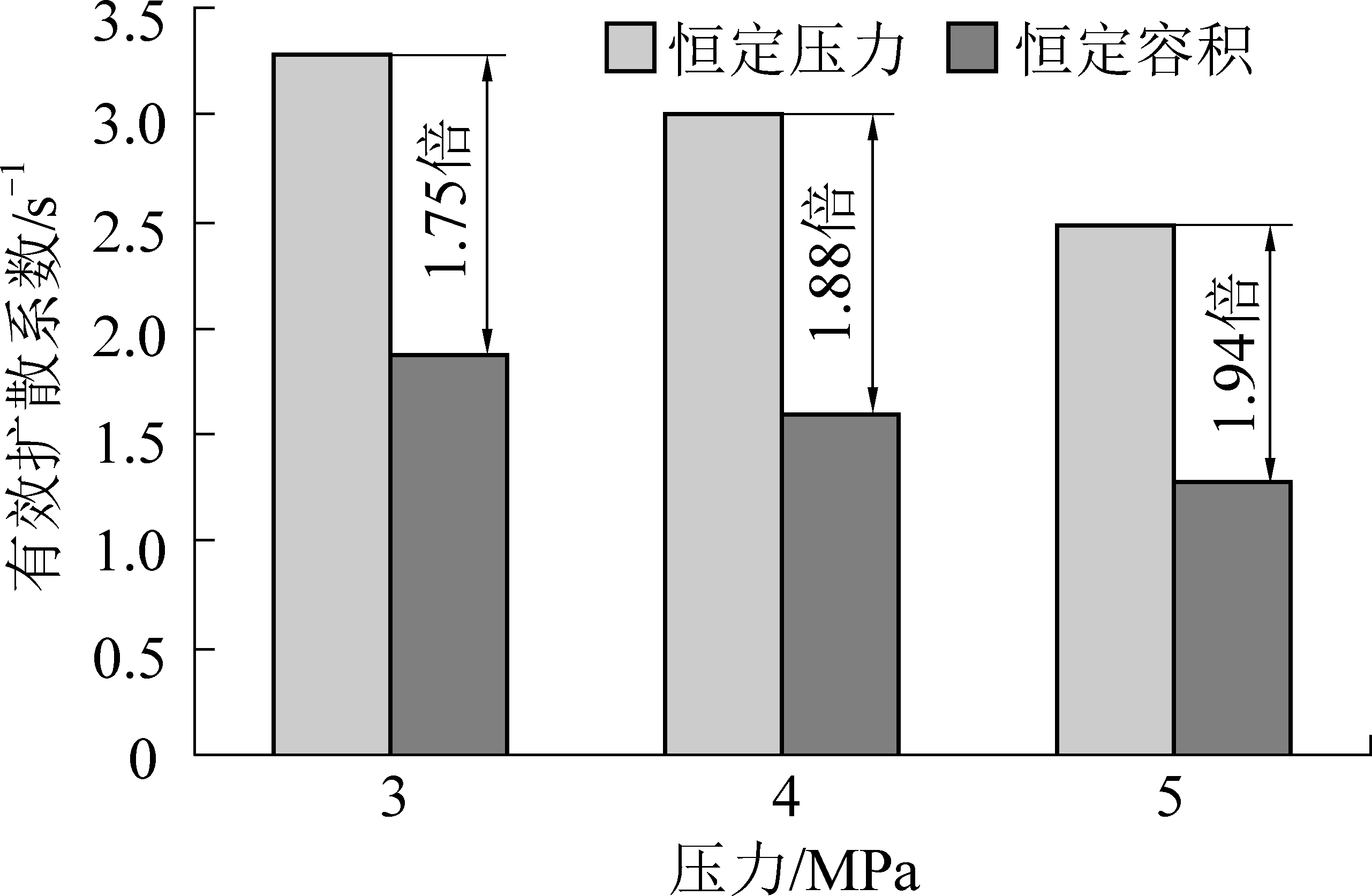
图7 不同拟合模型扩散系数对比
Fig.7 Comparison of diffusion coefficients with different models
2.4 定压定容扩散模型适用工程场景分析
从上述试验结果可知,定压条件的模型对于定容条件的吸附扩散试验有一定的拟合误差。而扩散系数最终用来评价瓦斯含量、瓦斯运移难度等物性参数,对瓦斯灾害治理、温室气体减排及瓦斯能源抽采极为重要。故而需要正确的理解各扩散系数的应用场景。对于实验室的吸附解吸试验而言,如果吸附源或者解吸边界保持压力恒定,则此时可以用定压条件的扩散模型进行动力学表征。而如果在密闭空间中进行吸附或解吸试验,则采用定容扩散模型更为科学。
而在工程中,因煤体距离煤壁或抽采钻孔孔壁距离不同,即距离恒定空气压力或抽采压力边界的距离不同,可以进行定性的类聚分析,如图8所示。对于卸压区内具有高渗率的煤体[20],因其经过应力损伤裂隙空间足够大,可近似认为是大气压力主导的定压边界,适用定压扩散模型;而对于应力集中区,其在某一点存在应力极大值σmax,使得渗透率最小,会近似产生阀门作用[20],对远离工作面的瓦斯形成圈闭效应,故而此区域的扩散系数应采用定容扩散系数来标定;与之相似,原始应力区同样也可用定容扩散系数来标定。以此类推,对于存在低渗区的区域,如断层、褶曲等部位[21],亦可用定容扩散系数来厘定。
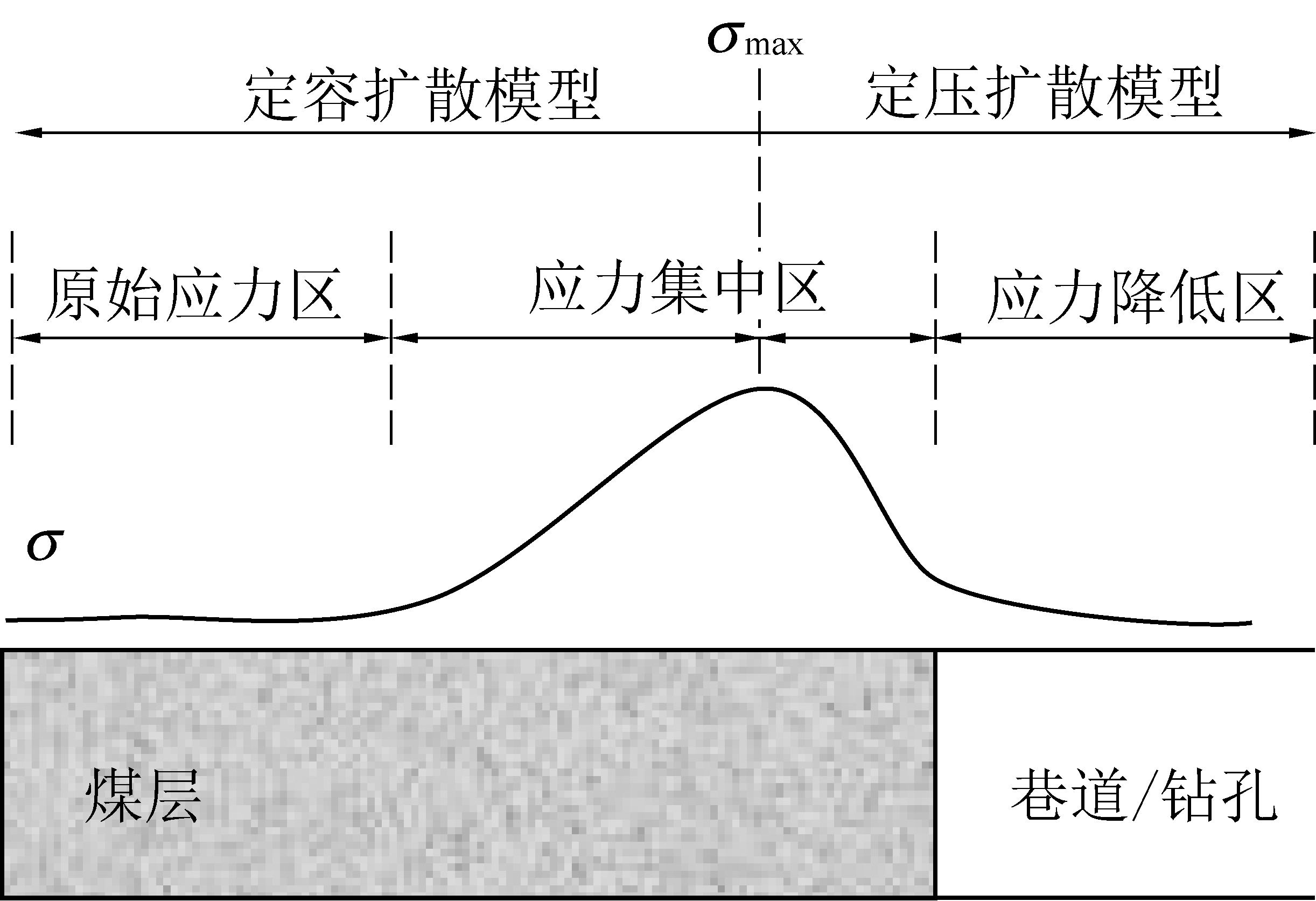
图8 扩散模型应用场景选择
Fig.8 Selection of the applications of different diffusion models
3 结 论
1)定容条件下,试验煤样吸附压力随吸附时间呈对数曲线形式逐渐降低。吸附初期,吸附扩散主要发生在半径较大的孔中,吸附扩散速度大。随之瓦斯分子进入壁面势能增大的微孔中,扩散阻力增大,扩散速度变小。初始压力为3、4和5 MPa条件下的平衡压力分别为2.36、3.30及3.90 MPa,而平衡吸附量分别为7.97、8.72及13.73 mL/g。
2)定容扩散模型更适合描述受限空间的吸附扩散系数。3种不同初始压力下,定压模型测得的扩散系数较之真正的定容扩散系数要分别大1.75、1.88和1.94倍,随着压力增加差异化逐渐增加。
3)定压扩散模型适合描述试验中的定压吸附或者定压解析试验,以及工程中煤层卸压区等高渗区的瓦斯运移规律。定容扩散模型适合描述试验中的定容吸附或者定容解析试验,以及工程中被煤层低渗区隔绝的瓦斯运移规律,如煤层应力集中区和原始应力区的瓦斯运移规律,或断层、褶曲等构造煤发育的部位。
[1] ZHAO Wei,CHENG Yuanping,PAN Zhejun,et al.Gas diffusion in coal particles:A review of mathematical models and their applications[J].Fuel,2019,252:77-100.
[2] 刘彦伟,刘明举.粒度对软硬煤粒瓦斯解吸扩散差异性的影响[J].煤炭学报,2015,40(3):579-587.
LIU Yanwei,LIU Mingju.Effect of particle size on difference of gas desorption and diffusion between soft coal and hard coal[J].Journal of China Coal Society,2015,40(3):579-587.
[3] 李志强,王登科,宋党育.新扩散模型下温度对煤粒瓦斯动态扩散系数的影响[J].煤炭学报,2015,40(5):1055-1064.
LI Zhiqiang,WANG Dengke,SONG Dangyu. Influence of temperature on dynamic diffusion coefficient of CH4 into coal particles by new diffusion model[J].Journal of China Coal Society,2015,40(5):1055-1064.
[4] CRANK J.The mathematics of diffusion[M].Oxford:Oxford University Press,1979.
[5] 杨其銮,王佑安.煤屑瓦斯扩散理论及其应用[J].煤炭学报,1986,11(3):87-93.
YANG Qiluan,WANG Youan.Theory of methane diffusion from coal cuttings and its application [J].Journal of China Coal Society,1986,11(3):87-93.
[6] 聂百胜,郭勇义,吴世跃,等.煤粒瓦斯扩散的理论模型及其解析解[J].中国矿业大学学报,2001,30(1):19-22.
NIE Baisheng,GUO Yongyi,WU Shiyue,et al.Theoretical model of gas diffusion through coal particles and its analytical solution[J].Journal of China University of Mining and Technology,2001,30(1):19-22.
[7] 安丰华,程远平,吴冬梅,等.基于瓦斯解吸特性推算煤层瓦斯压力的方法[J].采矿与安全工程学报,2011,28(1):81-86.
AN Fenghua,CHENG Yuanping,WU Dongmei,et al.Determination of Coal Gas Pressure Based on Characteristics of Gas Desorption [J].Journal of Mining and Safety Engineering,2011,28(1):81-86.
[8] 胡 彪,程远平,王 亮.原生结构煤与构造煤孔隙结构与瓦斯扩散特性研究[J].煤炭科学技术,2018,46(3):103-107,24.
HU Biao,CHENG Yuanping,WANG Liang.Study on porous structure and gas diffusion characteristics of primarystructure coal and tectonic coal[J].Coal Science and Technology,2018,46(3):103-107,24.
[9] BUSCH A,GENSTERBLUM Y.CBM and CO2-ECBM related sorption processes in coal:a review[J].International Journal of Coal Geology,2011,87(2):49-71.
[10] BUSCH A,GENSTERBLUM Y,KROOSS B M,et al.Methane and carbon dioxide adsorption-diffusion experiments on coal:upscaling and modeling[J].International Journal of Coal Geology,2004,60(2):151-168.
[11] 赵 伟.粉化煤体瓦斯快速扩散动力学机制及对突出煤岩的输运作用[D].徐州:中国矿业大学,2018.
ZHAO Wei.Diffusion dynamics of rapid desorption of gas from pulverized coal and its influence on transporting coal and rock in outbursts[D].Xuzhou:China University of Mining and Technology,2018.
[12] YANG Bin,KANG Yili,YOU Lijun,et al.Measurement of the surface diffusion coefficient for adsorbed gas in the fine mesopores and micropores of shale organic matter[J].Fuel,2016,181:793-804.
[13] PILLALAMARRY M,HARPALANI S,LIU S.Gas diffusion behavior of coal and its impact on production from coalbed methane reservoirs[J].International Journal of Coal Geology,2011,86(4):342-348.
[14] ZHAO Wei,CHENG Yuanping,YUAN Meng,et al.Effect of adsorption contact time on coking coal particle desorption characteristics[J].Energy & Fuels,2014,28(4):2287-2296.
[15] 李 惠,王福国,李振,等.六盘水煤田杨梅树向斜主要煤层孔隙结构特征研究[J].煤炭科学技术,2019,47(7):234-243.
LI Hui,WANG Fuguo,LI Zhen,et al.Study on pore properties of main coal seams of Yangmeishu syncline in Liupanshui coalfield[J].Coal Science and Technology,2019,47(7):234-243.
[16] 近藤精一,石川达雄,安部郁夫.吸附科学[M].李国希,译.北京:化学工业出版社,2005.
SEIICHI KONDO,ISHIKAWA,IKUO ABE.Adsorption science[M].LI Guoxi,Trans.Beijing:Chemical Industry Press,2006.
[17] 北川浩,铃木谦一郎.吸附的基础与设计[M].鹿政理,译.北京:化学工业出版社,1983.
KITAGAWA HAO,SUZUKI ICHIRO.The fundamentals and design for adsorption [M].LU Zhengli,Trans.Beijing:Chemical Industry Press,1983.
[18] DEBOER J H.The dynamical character of adsorption [J].Soil Science,1953,76(2):166.
[19] CLARKSON C R,BUSTIN R M.The effect of pore structure and gas pressure upon the transport properties of coal:a laboratory and modeling study.2.Adsorption rate modeling[J].Fuel,1999,78(11):1345-1362.
[20] 安丰华.煤与瓦斯突出失稳蕴育过程及数值模拟研究[D].徐州:中国矿业大学,2014.
AN Fenghua.Preparation and initiation of coal and gas outburst and its numerical modelling study[D].Xuzhou:China University of Mining and Technology,2014.
[21] 琚宜文.构造煤结构及储层物性[M].徐州:中国矿业大学出版社,2005.
JU Yiwen.Tectonic coal structure and its petrophysical features [M].Xuzhou:China University of Mining and Technology Press,2005.
