0 引 言
煤炭是我国的主要能源，在能源消费结构中占比达到60%以上[1]。 过去相当长的时期内煤炭开采属于高强度、粗放型开采，在追求产量增长的同时遗留和浪费了大量优质的煤炭资源，主要包括在多煤层开采过程中未开采的薄煤层、分层开采时为护顶而留的顶煤、中厚煤层开采过程中遗留的顶煤和底煤等。 通过对这些煤炭资源的复采，能有效提高采出率，延长矿井的服务年限[2-3]。 但在复采过程中，原煤层采出后冒落的顶板岩块经压实胶结形成再生顶板[4]。 再次开采扰动诱使顶板煤岩应力重新分布，顶板结构时空演化过程中应力诱导原生裂隙扩展和伴生次生裂隙。 当风流经过回采工作面时便渗入这些空隙形成漏风通道，空气中的氧气对顶板上覆遗煤表面进行缓慢氧化，随着热量的积聚，煤氧复合作用急剧加速，容易导致遗煤自燃，甚至引发瓦斯爆炸。 由于这种自燃是在顶板松散浮煤内部，外部很难检查发现，人们常对再生顶板裂隙漏风煤自然发火关注较少，防范意识较为薄弱。
近年来，广西百色州景煤矿、湖南牛马司铁箕山煤矿、河北省西庞煤矿、四川芙蓉白皎煤矿、吉林省辽源西安煤矿、铁法煤业大明煤矿、皖北煤电钱营孜煤矿等都由于再生顶板裂隙漏风发生不同程度的煤自燃火灾，轻者造成在工作面的大量设备被封闭冻结和回采煤量的大量损失，重者则引发气体爆炸(或气体毒化)，造成人员伤亡[5-7]。 另外我国神东矿区煤层数量多、厚度大，层间距离近。 当前大部分煤矿的上煤层已经采完，正进行的下煤层回采也遇到了由于再生顶板裂隙漏风诱发的复合采空区煤炭自燃问题。 泡沫流体材料因其优良的可泵送性和堆积性，其集堵漏控风、降温隔热、充填加固等应用性能为一体，是再生顶板裂隙漏风封堵及煤自燃防治的有效技术手段[8-10]。 而泡沫流体在再生顶板煤岩裂隙中的扩散规律是注浆施工设计的重要参考依据。
基于此，笔者开展再生顶板裂隙注泡沫流体扩散模型研究并对其施工参数及裂隙参数进行敏感性分析，以期为煤矿井下再生顶板注浆防灭火设计、施工提供一定的理论参考。
1 再生顶板裂隙注泡沫流体工程背景
再生顶板自下而上分为胶结再生带、弱胶结压实带、裂隙带和弯曲下沉带，如图1 所示。 胶结再生带主要成分为泥岩，其强度受结构面控制程度低，受应力时易发生变形和破碎。 巷道新鲜风流经变形破碎后的裂隙通道持续地流入再生顶板内部，为再生顶板裂隙带内遗煤自燃提供了良好的供氧环境。 借鉴采空区自燃“三带”分布规律，距漏风入口处一定距离的氧化带内的遗煤自燃危险性最大[11-13]。 为对再生顶板深部自燃危险区域进行注浆，需使用铺设注浆管的方式使浆液流入裂隙深部。 但再生顶板稳定性差，为避免钻孔附近顶板受力过大而发生垮冒，注浆管的伸入距离只能停留在裂隙带底部区域，因此泡沫流体只能通过裂隙通道间的渗流到达高处自燃危险区域。
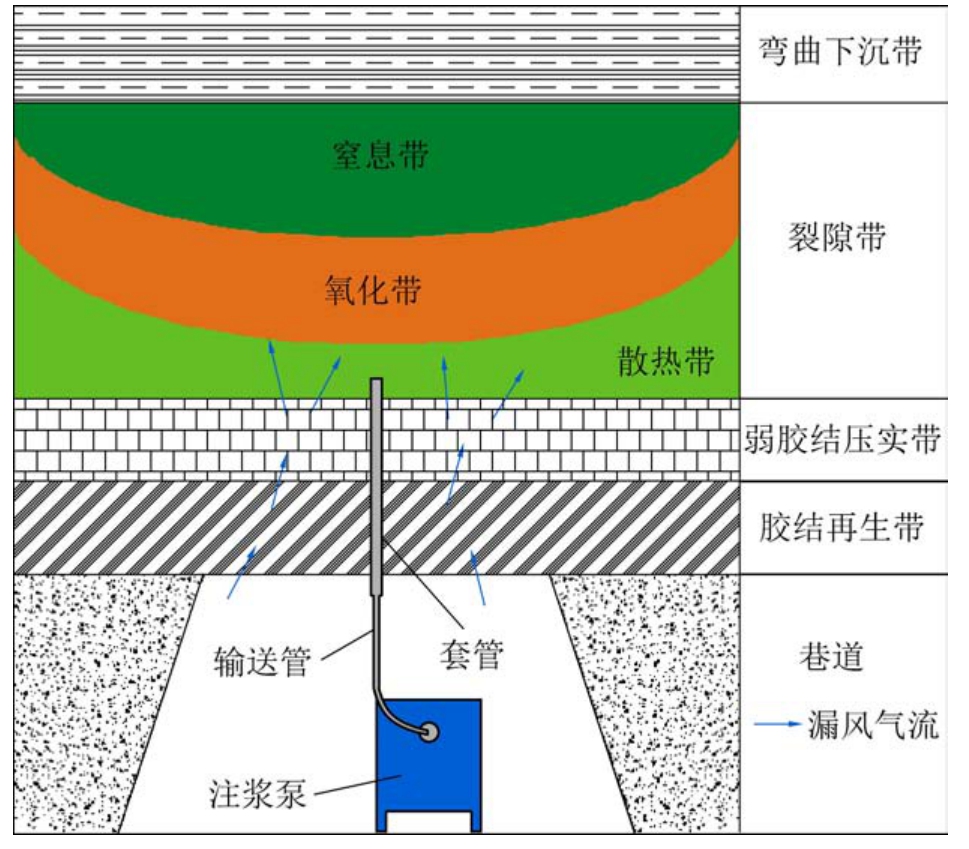
图1 再生顶板注浆示意
Fig.1 Schematic diagram of regenerated roof grouting
2 泡沫流体裂隙扩散数学模型
2.1 基本假设
再生顶板裂隙带属于复杂裂隙网络，裂隙通道分布随机性强，难以定量描述泡沫流体在每条裂隙通道的流动过程。 为研究方便，笔者仅考虑泡沫流体在单裂隙通道内的流动，并作以下基本假设:①泡沫流体视为黏度时变的宾汉流体[14]；②泡沫流体固化前的流变性保持不变；③裂隙物性参数不随注浆过程改变，且壁面光滑满足壁面无滑移条件；④泡沫流体只在裂隙通道内流动，不考虑煤岩基质渗流情况。
2.2 泡沫流体裂隙扩散运动方程
基于以上基本假设，考虑泡沫流体自注浆孔流出后沿裂隙通道径向流动，则泡沫流体流域内任意微元流体受力情况如图2 所示。
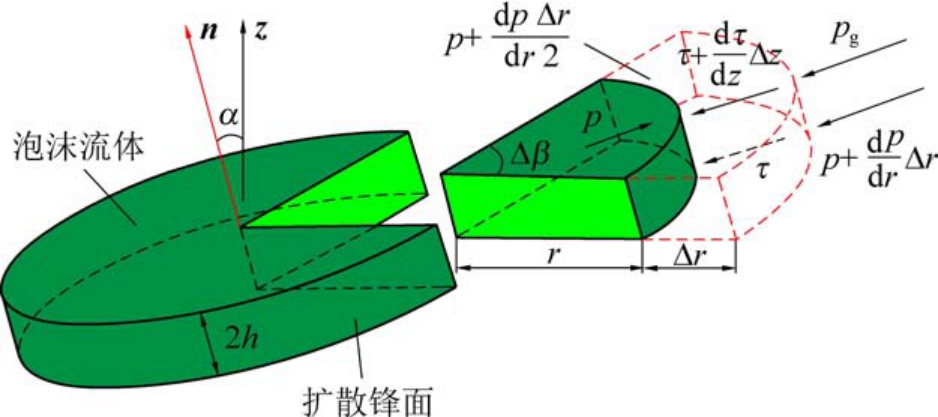
图2 裂隙内浆液扩散及浆液微元体受力示意
Fig.2 Schematic diagram of slurry diffusion in crack and force on slurry microelement body
图中向量n 为浆液流动平面的法向量；向量z为垂直方向向量； h 为裂隙开度的1/2，m。 受裂隙产状及重力影响，泡沫流体的扩散方式可分为趋于重力方向的低位流动和克服重力方向的高位流动。鉴于注浆管伸入距离的限制，泡沫流体将由低位向高位流动，则高位流动过程中微元体的受力平衡关系可由下式表示:
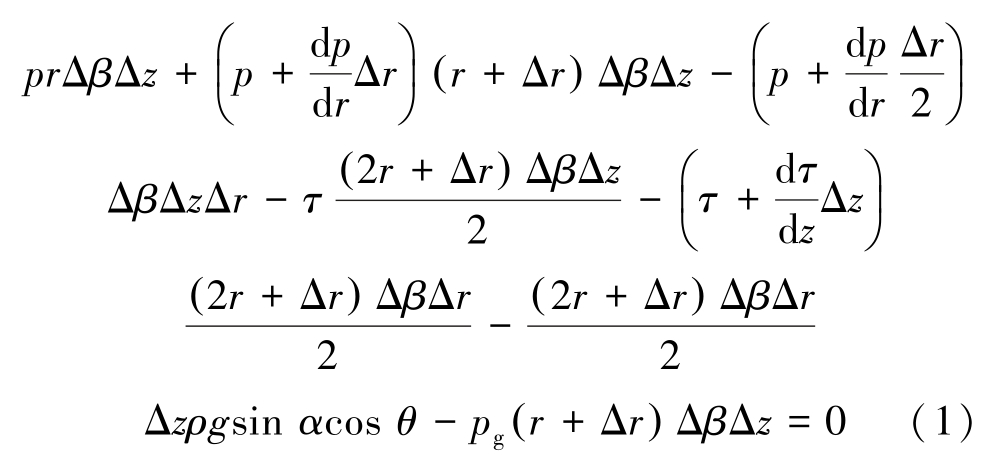
式中:p 为泡沫流体所受压力，Pa；r 为扩散距离，m；Δβ 为注浆孔与扩散增量形成的夹角，°；Δz 为浆液厚度，m；Δr 为扩散半径的增量，m； τ 为剪切应力，Pa； ρ 为密度，kg/m3； g 为重力加速度，m/s2； α 为倾角，(°)； θ 为倾向，(°)； pg 为原生介质压力，Pa。 忽略式中的高阶微量，式(1)可化简为
令
- ρgsin αcos θ-p ，对式(2)在 z 方向g上进行积分，可得:
广义上的Bingham 流体本构方程可表示为:
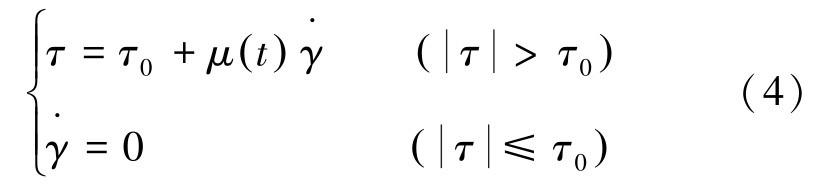
式中:τ0 为屈服应力，Pa；μ (t ) 为黏度时变关系式；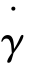
为剪切速率张量。 由于裂隙开度尺寸远小于走向尺寸，根据润滑近似后剪切速率张量可表示为:
泡沫流体黏度时变模型可由下式表示[15]:
式中:a 、 b、 c 均为黏度系数； t 为时间，s。 宾汉流体在流域内存在塞流区，在塞流区内剪切应力为0，流体以塞流速度uc 流动。 假设泡沫流体塞流区在z方向的跨度为2hc ，则泡沫流体截面上剪切应力分布可由下式表示:
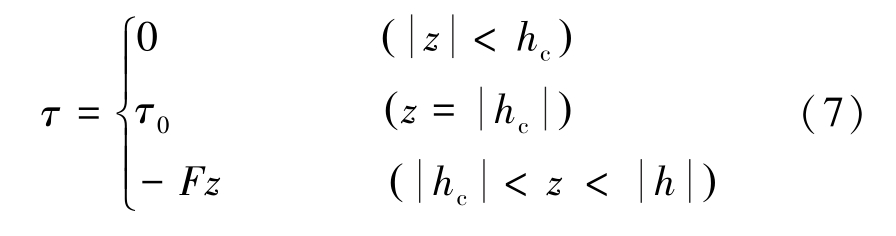
联立式(3)、式(4)、式(5)、式(6)、式(7)可得:
对式(8)在z 方向进行积分并代入壁面无滑移条件
，可得:
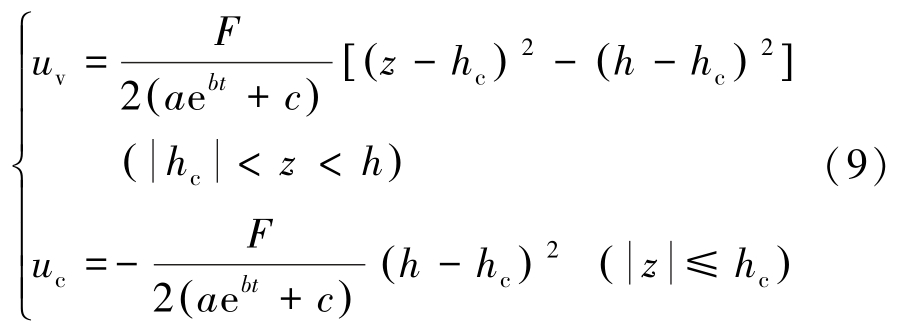
式中: uv 为变速区流速，m/s； uc 为塞流区流速，m/s。 则变速区注浆流量qv 和塞流区注浆流量qc 为
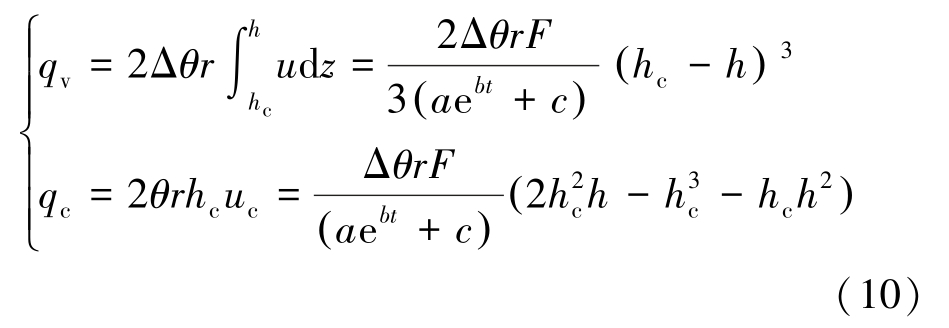
注浆总流量可表示为2 个区域注浆流量之和:
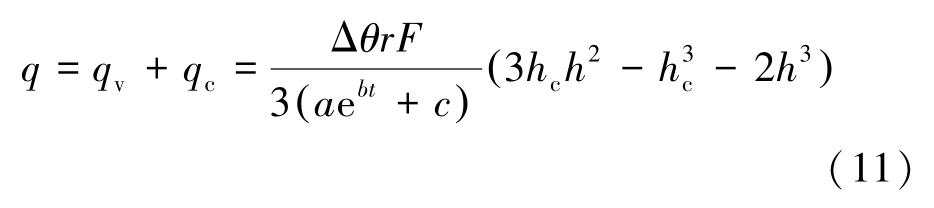
结合式(7)，式(11)可改写为:
屈服应力τ0 远小于流动过程的水力梯度，因此忽略式(12)三阶微量。 式(12)简化并整理为:
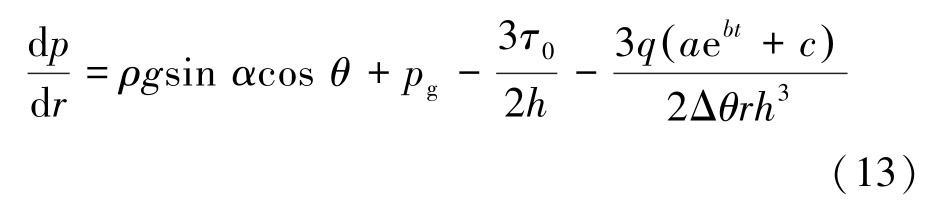
式(13)为泡沫流体微元体流动过程水力梯度与流量关系式。 对式(13)在r 方向进行积分，并代入边界条件
= p0，得到:
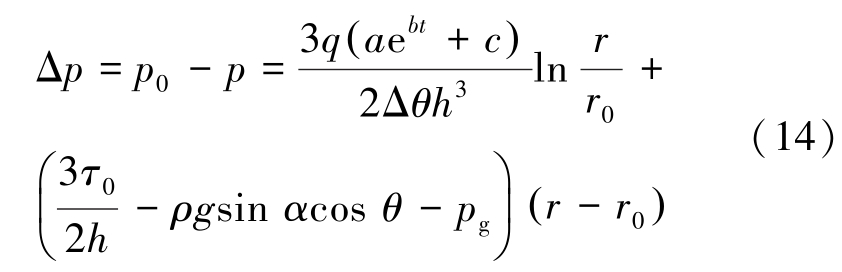
式中:r0 为注浆孔半径，m；p0 为注浆孔处的压力，Pa。 相对于浆液的扩散半径，注浆孔半径可以忽略。 式(14)可简化为
式(15)反映了注浆流量与扩散距离关系。 当压差一定时，注浆总流量与扩散距离呈负相关关系。但注浆流量的监测增加了现场施工成本，在未探明裂隙空间体积的情况下注浆流量不适合作为注浆评估指标。 而扩散距离和注浆时间之间的关系式更符合现场施工的需要[16-17]，因此对式(15)进行变换，得出注浆总流量的表达式:
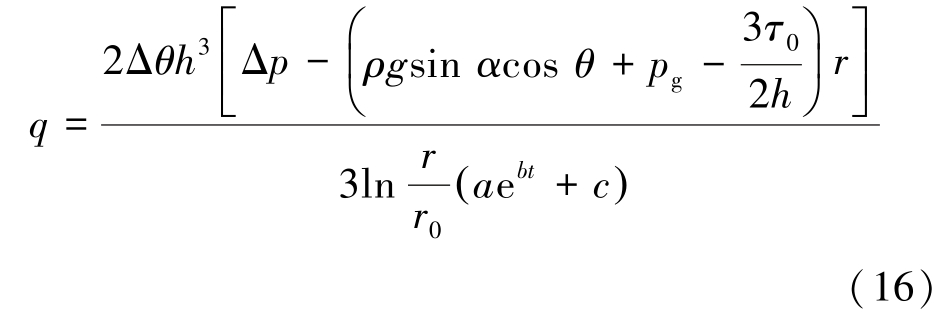
根据质量守恒定律，单位时间内注浆孔注入的泡沫流体体积应等于泡沫流体扩散半径的增量，即
结合式(16)，令
，可得:
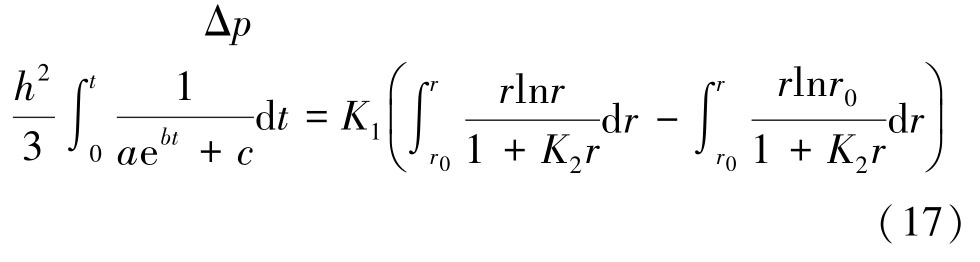
对式(17)等号左右同时积分求解，可得:
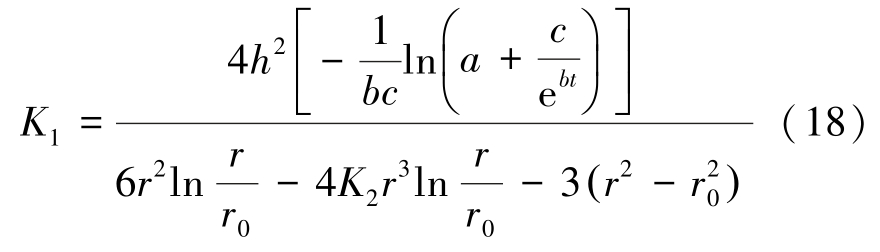
定义黏性特征时间t* 以表征泡沫流体黏度与时间的耦合关系，t* 定义式为
基于以上定义，式(18)可化简整理为
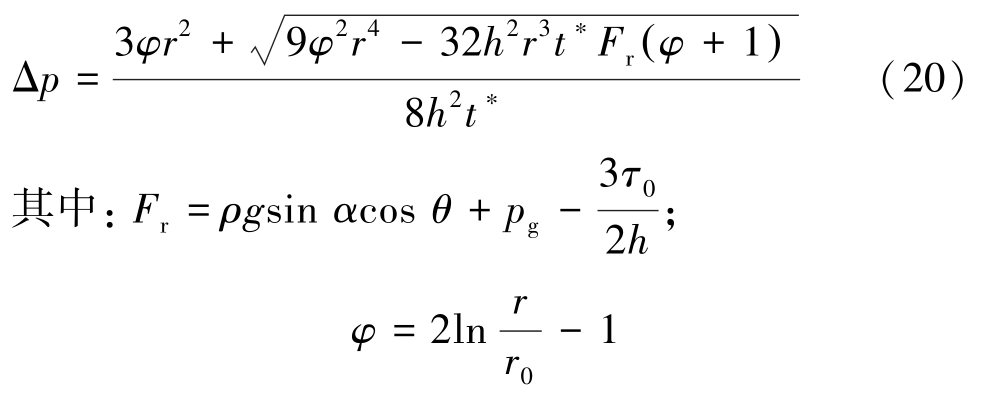
上式即泡沫流体在任意产状裂隙中注浆扩散数学模型，由模型可得出泡沫流体扩散距离的影响因素有施工参数(含注浆压力、注浆孔半径)、裂隙参数(含裂隙开度、倾角、倾向、裂隙原始介质压力)和浆液参数(含屈服应力、黏度、密度)。 式(20)经整理后可得出黏性特征时间表达式:
3 算例验证
为对上述泡沫流体裂隙扩散数学模型的合理性进行验证，建立数值模型如下:①数值模型为 1 m×1 m×6 mm 的倾斜平板裂隙，倾角 30°，倾向60°；②注浆口位于模型中心，施加压力入口边界，注浆压力设置为12 kPa；③出口边界位于模型四周，设施加压力出口边界，出口压力为2 kPa；④上下边界设置为无滑移壁面。 数值模型使用结构化网格进行离散并使用 ANSYS FLUENT 进行数值求解[18-19]；⑤泡沫流体的密度设置为556 kg/m3、屈服应力设置为5 Pa、黏度系数 a、b、c 分别设置为 0.5、0.005、5。 将注浆过程看作对裂隙内介质的驱替过程，假设裂隙内原生介质为空气，初始时刻模型内充满空气，并使用VOF 算法捕捉两相交界锋面。
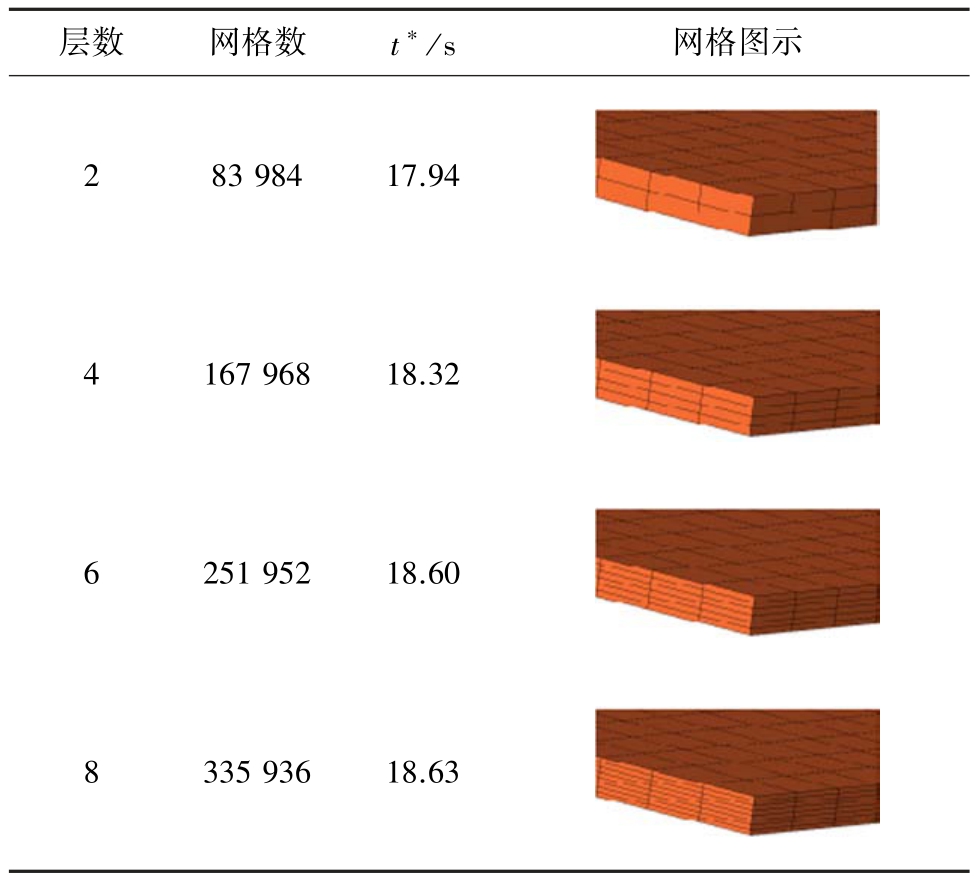
为避免网格数量不同对结果产生的误差，进行了网格无关性验证。 通过改变裂隙开度方向网格层数控制计算域总网格数量。 以泡沫流体扩散到0.3 m 处的黏性特征时间为检验参数，不同网格数量下黏性特征时间见表1。 随着厚度方向网格层数增加，检验参数的相对误差逐渐减小。 当网格层数大于6 层之后，计算结果的相对误差低于2%。 兼顾计算精度和计算资源，采用第3 组网格划分结果进行计算。 数值计算得出泡沫流体扩散流域内压力分布云图如图3 所示。
表1 网格无关性验证
Table 1 Grid independence verification
?
基于图3 的数值结果，提取泡沫流体在不同流动时间时对应的扩散距离和扩散锋面压力代入公式(21)计算出黏性特征时间，并与数值模型计算得出的结果进行对比，得出数值模型与数学模型在不同扩散距离处的黏性特征时间相对误差如图4 所示。
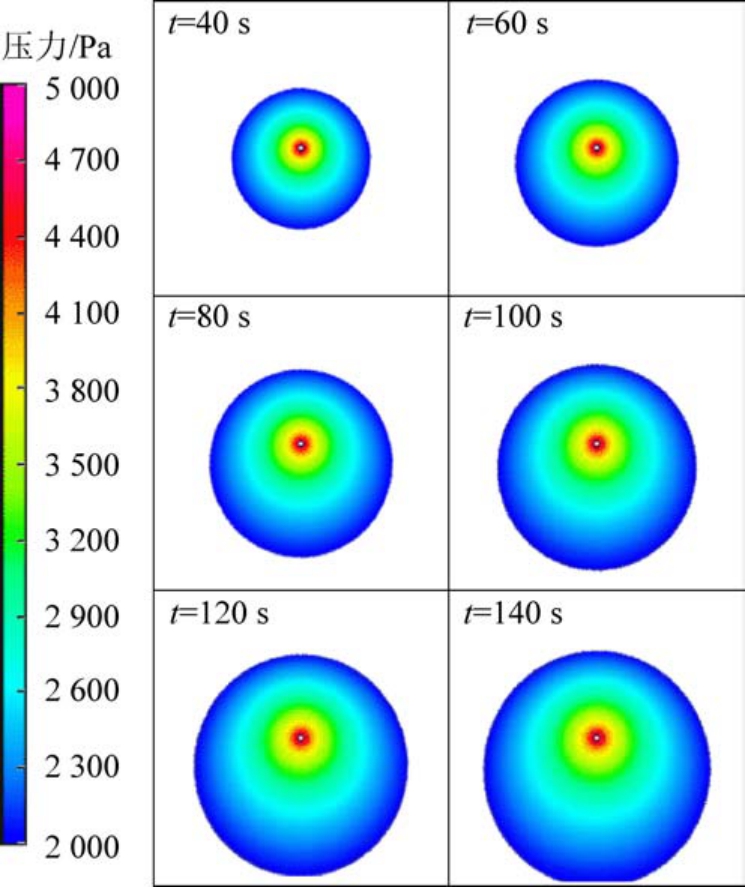
图3 扩散流域内压力分布云图
Fig.3 Pressure distribution in diffusion region
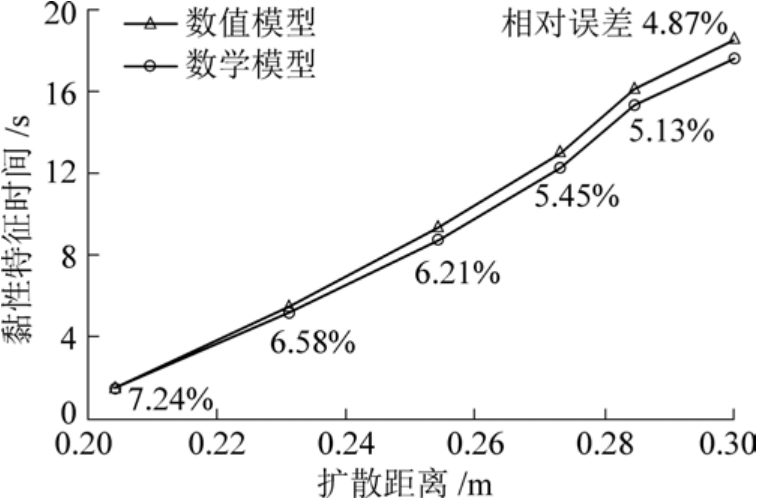
图4 数学模型与数值模型相对误差
Fig.4 Error between mathematical model and numerical model
由图4 可知，数值模型与数学模型得出的黏性特征时间随扩散距离变化规律具有一致性，但数值模型结果均大于数学模型，这是由于解析解在推导时省略了高阶屈服应力及注浆孔半径的影响，导致扩散到相同距离所需要的时间比数值模型所需时间更少。 二者的相对误差随着扩散距离的增加而减小，符合扩散距离越大，注浆孔尺寸影响程度越小的规律。 综上所述，数学模型与数值模型的相对误差均低于10%，表明数学模型具有一定的合理性。
4 参数敏感性分析
根据泡沫流体裂隙扩散数学模型可得泡沫流体扩散距离的影响因素有施工参数(含注浆压力、注浆孔半径)、裂隙参数(含裂隙开度、倾角、倾向、裂隙原始介质压力)和浆液参数(含屈服应力、黏度、密度)。 在现场再生顶板裂隙压注泡沫流体过程中，由于制备好的泡沫流体的浆液参数是固定的，因此下文开展施工参数和裂隙参数的敏感性分析。 黏性特征时间与扩散距离的关系反应了泡沫流体在黏度与时间耦合变化过程中的扩散规律，扩散到相同距离的黏性特征时间越短，表明泡沫流体的扩散能力越强。 因此改变单一参数值，以黏性特征时间为评价指标，探究不同单一影响因素对泡沫流体扩散距离的影响规律。
4.1 施工参数
施工参数中注浆压力与注浆孔半径对泡沫流体扩散距离影响如图5 所示。
由图5a 可知，注浆压力越大，扩散到相同距离的黏性特征时间越小，表明增加注浆压力能提高泡沫流体的扩散距离。 但注浆压力增幅在不同时期对泡沫流体扩散距离的影响不同。 在注浆前期，注浆压力的增加对泡沫流体扩散距离的影响程度较小。而在注浆后期，注浆压力对扩散范围的影响较为显著。 值得注意的是，注浆压力在22 kPa 之后对扩散距离的贡献逐渐降低。 由图5b 可知，扩散到相同距离所需的黏性特征时间随注浆孔半径的增大而减小。 这是因为更大的注浆孔半径提供了更大的流量，使得泡沫流体获得了一个更大的初始注浆速度。
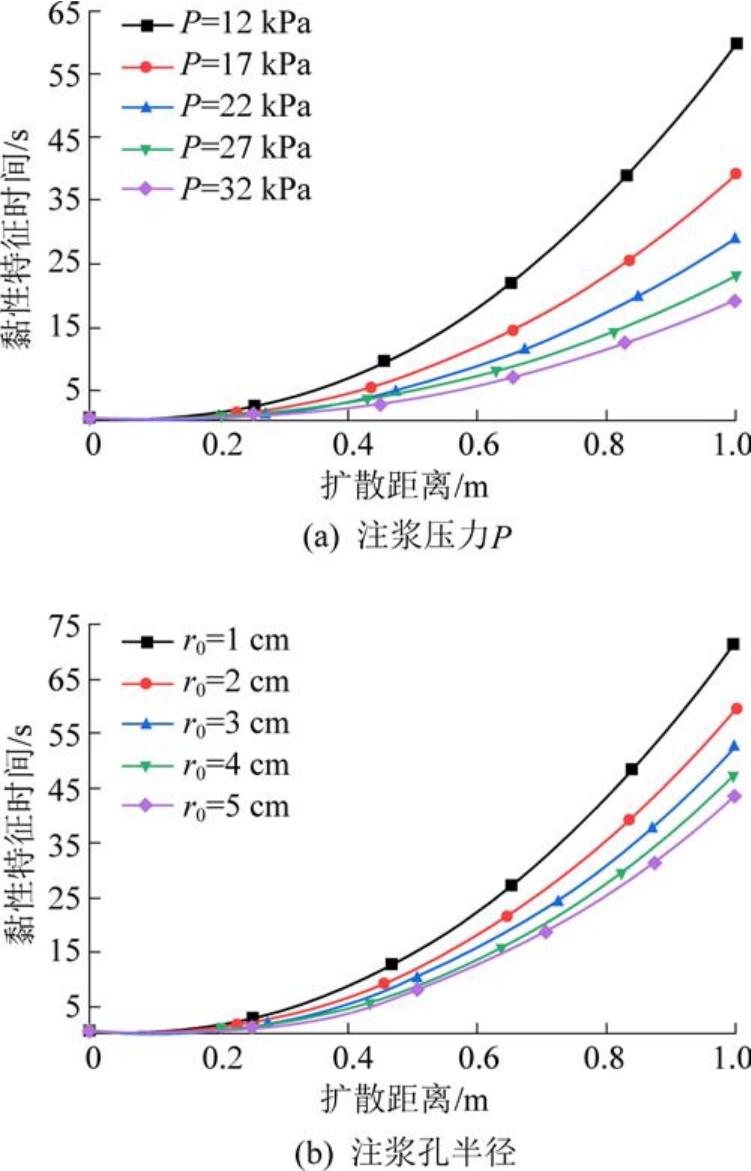
图5 不同施工参数影响下扩散距离随黏性特征时间变化规律
Fig.5 Diffusion distance varies with the characteristic time of viscosity under the influence of different construction parameter
4.2 裂隙参数
裂隙参数中裂隙开度、倾向、倾角及原生介质压力对泡沫流体扩散距离影响如图6 所示。
由图6a 和图6b 可知，倾向和倾角对扩散距离的影响不同。 黏性特征时间随着倾角的增大而增大，但随着倾向的增大而减小。 因为倾角越大，泡沫流体所需克服的重力分量也越大，导致流动过程的阻力也越大，因此在相同黏性时间下扩散距离也越小。 倾向的改变同样也会影响重力在泡沫流体流动方向的分量，但对泡沫流体扩散距离的影响程度较小。 由图6c 可知，原生介质压力越大，扩散到相同距离的黏性特征时间越长。 裂隙注浆过程即是对裂隙中原生介质的驱替过程，因此原生介质压力越大，泡沫流体流动过程所受阻力越大。 由图6d 可知，裂隙开度越大，扩散到相同距离所需的黏性特征时间越小。 裂隙开度在2～4 mm 时黏性特征时间的降幅最大，当裂隙开度超过4 mm 之后黏性特征时间的降幅减小。 当裂隙开度从2 mm 增加到4 mm 时，扩散到1 m 处的黏性特征时间从136 s 下降到34 s，降幅为75%；当裂隙开度从3 mm 增加到6 mm 时，扩散到1 m 处的黏性特征时间从60 s 下降到15 s，降幅同样为75%，表明在裂隙开度变化过程中黏性特征时间的下降速率保持不变。
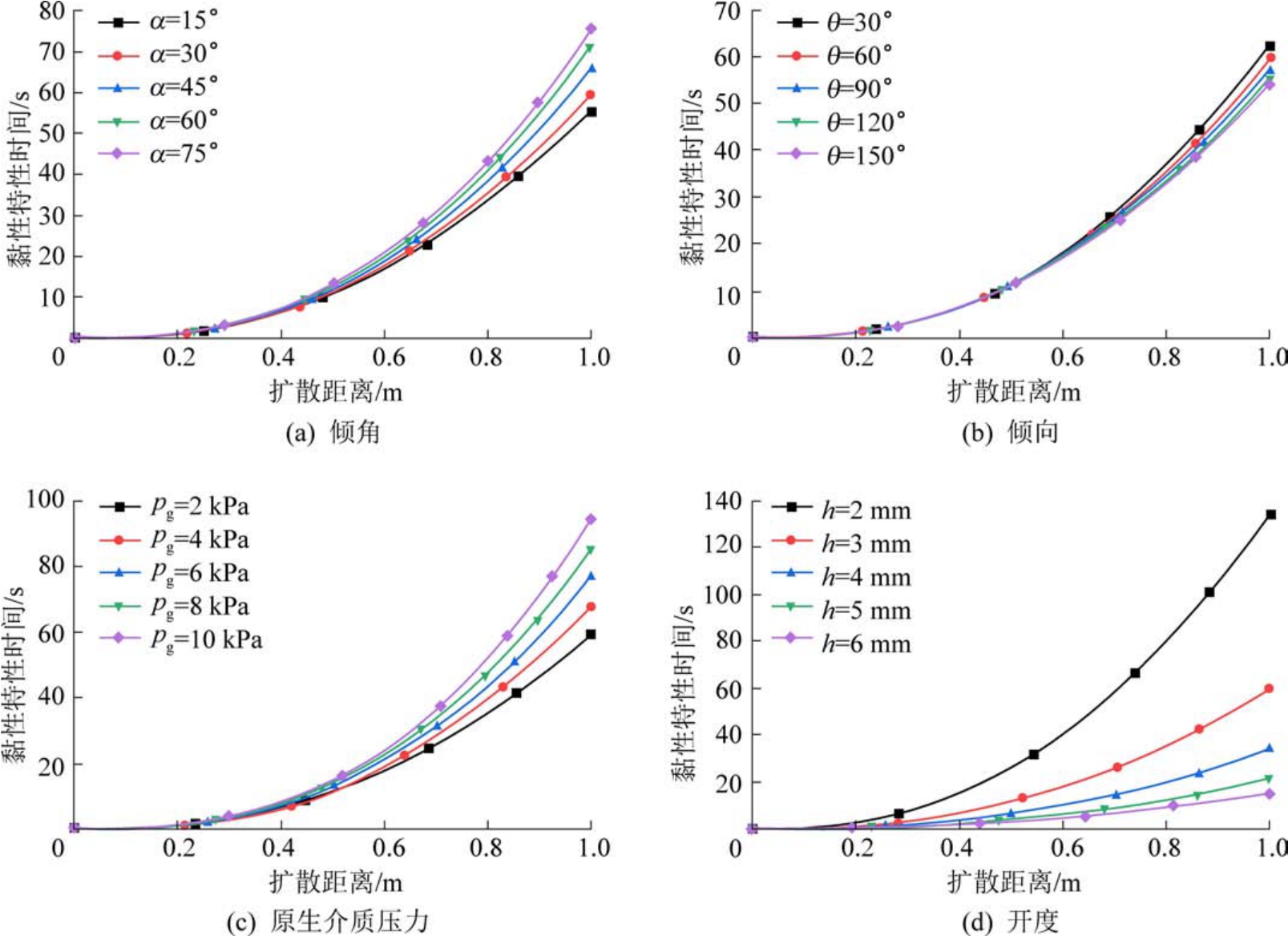
图6 不同裂隙参数影响下扩散距离随黏性特征时间变化规律
Fig.6 Diffusion distance varies with the time characteristic of viscosity under the influence of different fracture parameters
4.3 参数敏感度计算
为了进一步定量分析施工参数及裂隙参数对泡沫流体扩散距离的影响的敏感度，选取流动黏性特征时间15 s 时对应的扩散距离作为评价指标，则敏感度可由式(22)定义[20]:
式中:η 为敏感度；W* 为影响参数发生变化后对应的扩散距离，m； W0 为影响参数在初始值时对应的扩散距离，m；ΔY 为影响参数的变化率，%。 计算出不同参数在(-60%，60%)范围内不同变化率下的敏感度如图7 所示。
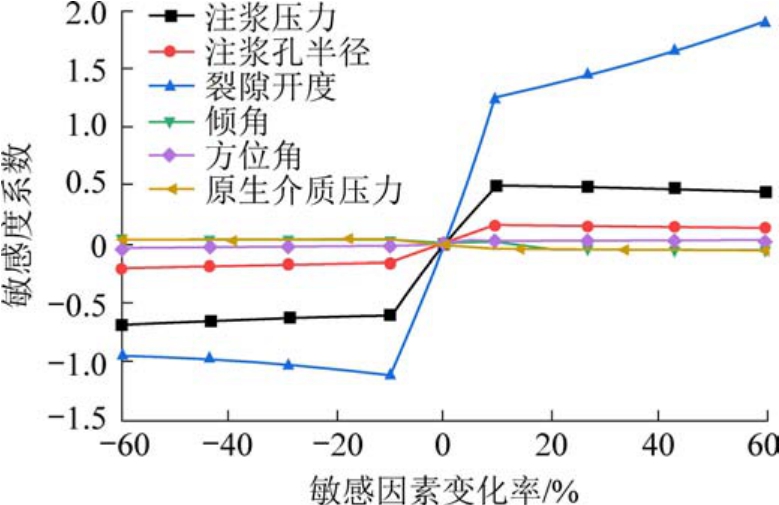
图7 敏感度系数随影响因素变化率变化曲线
Fig.7 Curves of sensitivity coefficient with the change rate of influencing factors
由图7 可知，裂隙开度与注浆压力的敏感度系数随影响因素变化率变化较其他影响因素更为明显。 在变化区间[-10%，10%]之内，各影响参数的敏感度系数随变化率增加幅度大。 当变化率超过10%之后，注浆孔半径与注浆压力的敏感度系数开始出现下降，而裂隙开度敏感度系数仍呈上升趋势。其中倾角的敏感度系数在[10%，20%]区间内出现下降，之后保持不变。 综上所述，敏感度因素变化的合理区间为[-10%，10%]，在其中，裂隙开度对扩散距离影响最大，注浆压力次之，倾角和原生介质压力影响最小。
5 结 论
1)基于再生顶板裂隙注泡沫流体工程背景，开展了泡沫流体在裂隙中的受力和流动分析，推导得出了泡沫流体在含原生介质阻滞作用的任意产状裂隙中的流动扩散数学模型，并基于泡沫流体的黏度时变特性提出了黏性特征时间表达式。
2)采用ANSYS FLUENT 软件构建了泡沫流体在再生顶板裂隙中的扩散数值模型，并模拟得出了泡沫流体裂隙扩散体积分数和裂隙内流域压力分布云图。 基于泡沫流体在不同扩散距离时对应的锋面压力数据，计算数值模型与数学模型在不同扩散距离处的黏性特征时间，其相对误差均低于10%，表明数学模型具有一定的合理性。
3)开展了泡沫流体再生顶板裂隙注浆扩散过程中的施工参数(含注浆压力、注浆孔半径)及裂隙参数(含裂隙开度、倾角、倾向、裂隙原始介质压力)对扩散规律的影响，并定量计算了参数对扩散过程的敏感度，得出裂隙开度对扩散距离的影响最大，注浆压力次之，倾角和原生介质压力影响最小。
[1]袁 亮.我国煤炭资源高效回收及节能战略研究[J].中国矿业大学学报:社会科学版，2018，20(1):4-13.YUAN Liang.Strategies of high efficiency recovery and energy saving for coal resources in china[J].Journal of China University of Mining and Technology:Social Sciences，2018，20(1):4-13.
[2]刘 畅，弓培林，王 开，等.复采工作面过空巷顶板稳定性[J].煤炭学报，2015，40(2):314-322.LIU Chang，GONG Peilin，WANG Kai，et al.Roof stability for repeated mining workface passing through abandoned parallel gateway[J].Journal of China Coal Society，2015，40(2):314-322.
[3]张俊文，赵景礼，王志强.近距残煤综放复采顶煤损伤与冒放性控制[J].煤炭学报，2010，35(11):1854-1858.ZHANG Junwen，ZHAO Jingli，WANG Zhiqiang.Top coal damage and caving characterizes control of residual coal repeated mining adopted longwall top-coal caving in contiguous seams[J].Journal of China Coal Society，2010，35(11):1854-1858.
[4]马文强，王同旭，马紫阳.复采采场再生顶板结构及支架载荷确定[J].岩土工程学报，2017，39(10):1892-1900.MA Wenqiang， WANG Tongxu， MA Ziyang.Structure of regenerated roof and determination of support load in re-mining stope[J].Chinese Journal of Geotechnical Engineering，2017，39(10):1892-1900.
[5]马 威，米楚明，王 祥.西庞煤矿采空区遗煤复采煤层自燃火灾的防治[J].煤矿安全，2010，41(4):31-33.MA Wei， MI Chuming， WANG Xiang.Prevention and control of spontaneous fire in residual coal mining seam in Xipang Coal Mine[J].Safety in Coal Mines，2010，41(4):31-33.
[6]黎经雷，牛会永，鲁 义，等.风速对近距离煤层采空区漏风及煤自燃影响研究[J].煤炭科学技术，2019，47(3):156-162.LI Jinglei，NIU Huiyong，LU Yi，et al.Study on effect of wind speed to air leakage and spontaneous combustion in goaf of contiguous seams[J].Coal Science and Technology，2019，47(3):156-162.
[7]黄 戈，张 勋，王继仁，等.近距离煤层上覆采空区自燃形成机理及防控技术[J].煤炭科学技术，2018，46(8):107-113.HUANG Ge， ZHANG Xun， WANG Jiren， et al.Formation mechanism and prevention technology of spontaneous combustion occurred in overburden goaf in contiguous seams[J].Coal Science and Technology，2018，46(8):107-113.
[8]鲁 义.防治煤炭自燃的无机固化泡沫及特性研究[D].徐州:中国矿业大学，2015.LU Yi.Study on the inorganic solidified foam and its characteristics for preventing and controlling spontaneous combustion of coal[D].Xuzhou:China University of Mining and Technology，2015.
[9]鲁 义，施式亮，王海桥，等.防灭火水泥基泡沫的凝结特性测试新方法及应用[J].材料科学与工程学报，2017，35(6):957-962.LU Yi，SHI Shiliang，WANG Haiqiao，et al.New method to the test setting time of foam cement for mine fire control and its application[J].Journal of Materials Science and Engineering，2017，35(6):957-962.
[10]LU Yi，SHI Shiliang，WANG Haiqiao，et al.Thermal characteristics of cement microparticle-stabilized aqueous foam for sealing high-temperature mining fractures[J].International Journal of Heat and Mass Transfer，2019，131:594-603.
[11]朱建芳，秦跃平，杨小彬，等.采空区自燃理论模型的无因次分析与应用[J].煤炭学报，2016，41(10):2626-2630.ZHU Jianfang，QIN Yueping，YANG Xiaobin，et al.Dimensionless analysis and application on the mathematical model for spontaneous combustion in goaf[J].Journal of China Coal Society，2016，41(10):2626-2630.
[12]关万里.神东矿区采空区遗煤自然发火规律研究[J].煤炭科学技术，2015，43(S2):71-75.GUAN Wanli.Research on residual coal spontaneous combustion law for mine goaf in Shendong Mining Field[J].Coal Science and Technology，2015，43(S2):71-75.
[13]吕英华，任显财，胡海峰.煤矿采空区高温区域分析界定及治理[J].煤炭科学技术，2017，45(S1):94-99.LYU Yinghua，REN Xiancai，HU Haifeng.Analysis and management of high temperature area in mine goaf[J].Coal Science and Technology，2017，45(S1):94-99.
[14]TIAN Zhaojun，LU Yi，LIU Shimin，et al.Application of inorganic solidified foam to control the coexistence of unusual methane emission and spontaneous combustion of coal in the luwa coal mine，China[J].Combustion Science and Technology，2019，1-19.
[15]LU Yi.Laboratory study on the rising temperature of spontaneous combustion in coal stockpiles and a paste foam suppression technique[J].Energy & Fuels，2017，31(7):7290-7298.
[16]柳昭星，靳德武，尚宏波，等.矿区岩溶裂隙岩体帷幕截流注浆参数确定研究[J].煤炭科学技术，2019，47(6):81-86.LIU Zhaoxing，JIN Dewu，SHANG Hongbo，et al.Study on determination of curtain closure grouting parameters of fractured rock mass in karst mining area[J].Coal Science and Technology，2019，47(6):81-86.
[17]郭志文.综采面断层带泥质破碎岩体渗流特性及注浆加固技术研究[D].徐州:中国矿业大学，2019.GUO Zhiwen.Study on seepage characteristics and grouting reinforcement technology of argillaceous broken rock mass in fully mechanized face fault zone[D].Xuzhou:China University of Mining and Technology，2019.
[18]刘 玉，韩 雨，张 强，等.水沙混合物裂隙渗流特性分析[J].煤炭学报，2019，44(3):875-881.TANG Chuanjin，YAO Qiangling，WANG Weinan，et al.Experimental study on damage characteristics of sandy mudstone under the action of water[J].Journal of China Coal Society，2019，44(3):881-889.
[19]董 浩.基于浆液性能控制的岩溶裂隙注浆扩散规律及应用研究[D].北京:北京交通大学，2017.DONG Hao.Study on diffusion law and application of karst fracture grouting based on grout performance control[D].Beijing:Beijing Jiaotong University，2017.
[20]韩 烨.考虑黏度时变性的宾汉姆浆液注浆扩散机理研究[D].青岛:山东大学，2014.HAN Ye.Study on the mechanism of grouting diffusion of bingham grouts with viscosity variation[D].Qingdao: Shandong University，2014.
