0 引 言
煤炭资源深部开采过程中，高应力常引起软岩巷道开挖大变形、支护失效，这些破坏与失效问题很难用经典的围岩弹塑性力学理论来解释。
为了探明深部软岩巷道破坏机制，实现巷道有效支护，控制软岩开挖工程的大变形等问题，学者们开展了大量的研究[1-4]。 为了研究巷道开挖卸荷效应，CARTER 等[5]计算分析了理想条件下长隧洞开挖围岩的瞬态响应；FAKHIMi 等[6]研究了开挖砂岩巷道破裂发育规律；MARTIN 等[7]分析了开挖引起的巷道应力分布规律；孙钧[8]给出了开挖卸荷的当量计算方法；侯公羽等[9]计算了“开挖卸荷”引起的“空间效应”；SENENT 等[10]分析了开挖面支护力低于“临界”或“崩溃”压力的极限值；彭瑞[11]研究了开挖卸荷效应、锚杆支护存在的时机和方式。 为了研究巷道围岩结构性失稳机制，董方庭等[12]提出了松动圈概念，为地下软岩工程的支护方案设计提供依据；康红普[13]提出围岩关键承载结构模型；余伟建等[14]提出了叠加承载拱力学模型。
综上所述，学者们针对深埋巷道开挖失稳研究提出了较多的理论和模型，目前针对围岩承载结构中考虑剪应力、开挖卸荷效应影响鲜有报道。 笔者基于统一强度准则和软岩应变软化模型，在软岩巷道开挖面后方一定范围内，建立围岩卸荷力学模型，考虑开挖卸荷效应，分析巷道开挖对原岩应力阈值、塑性范围、岩层移动规律、支护参数设计的影响；基于围岩次生应力分布特征，提出围岩力学承载结构划分新方法，并结合算例分析岩性软化程度对围岩力学承载结构稳定性的影响。
1 理论模型建立
1.1 基本假设
为便于建立围岩力学模型，采用弹塑性理论分析开挖卸荷作用下软岩巷道围岩变形破坏特征，本文做出如下假设:①围岩为均质且各向同性体；②巷道埋深足够深，且轴向为足够长的等截面柱体，可简化为平面应变问题；③开挖前巷道处于静水压力场；④巷道开挖后，围岩可划分为破碎区(半径Rf)和软化区(半径Rs)。
1.2 基本方程
1.2.1 统一强度准则
在平面应变模型中根据 Levy-Mises 本构关系[15]为
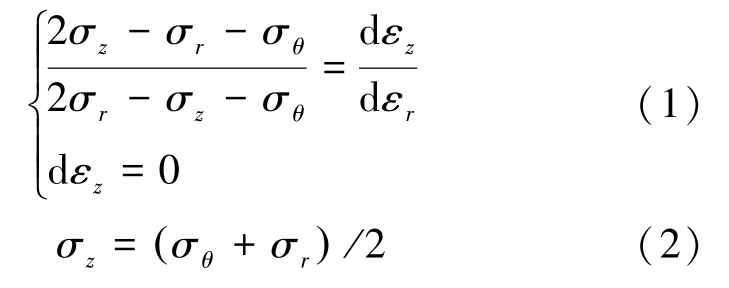
式中: σθ 、 σr 、 σz 分别为巷道围岩中切向、径向和轴向应力；εz 、εr 分别为轴向和径向应变。
经整理得统一强度准则表达式为
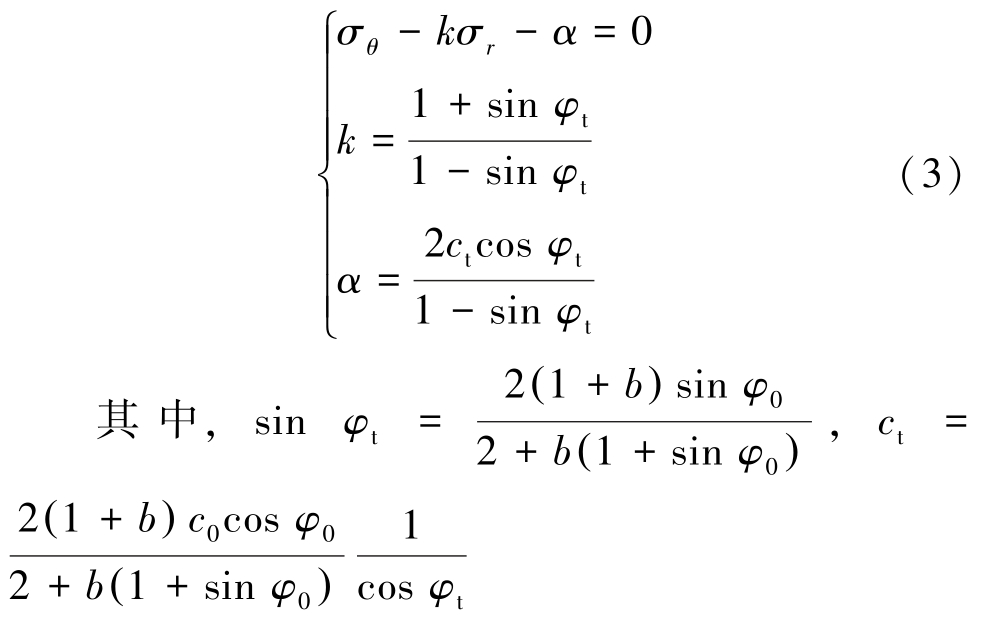
式中:c0为初始黏聚力；φ0为初始内摩擦角；b 为中间主剪应力及其作用面上法向正应力对材料破坏的影响程度，取 0、0.5 和 1.0 时，分别对应 Mohr-Coulomb准则、Von-Mises 准则和双剪准则。
于是，可得软化区、破碎区强度准则表达式为
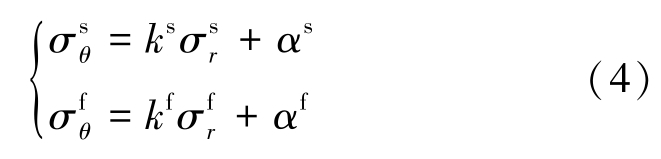
式中:ks 、 αs 、 kf 、 αf 分别为软化区、破碎区围岩抗剪强度参数。 本文中不论是下标或上标s 和f 均分别代表软化区和破碎区的相关参数。
1.2.2 平衡微分方程、几何方程
忽略体积力，平衡微分方程为
考虑平面应变问题，几何方程为
式中:εθ 为切向应变；u 为径向位移；r 为围岩内任意点到巷道中心距离。
1.3 软岩应变软化、扩容本构模型
1.3.1 应变软化模型
在软化阶段，岩石抗剪强度折减表达式为
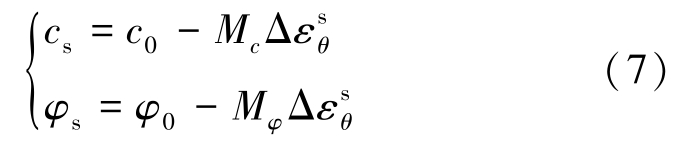
式中:cs为软化区黏聚力；φs为软化区内摩擦角；Mc、Mφ分别为黏聚力和内摩擦角软化模量；Δ εs θ 为软化区切向应变增量。
围岩参数软化模型如图1 所示。
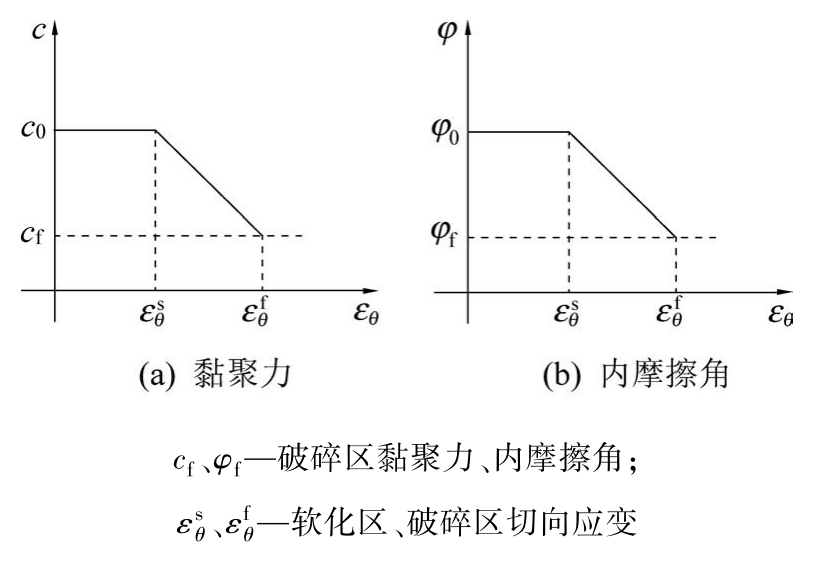
图1 强度参数软化模型
Fig.1 Soften model of strength parameters
1.3.2 体积扩容模型
考虑体积应变不为零，软岩应变关系为
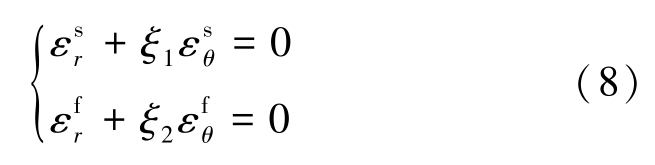
式中:ξ1、ξ2 分别为软化区、破碎区的扩容系数，其之间关系为 ξ1 ≥ ξ2。
依据文献[15]，软化区扩容系数ξ1 定义为
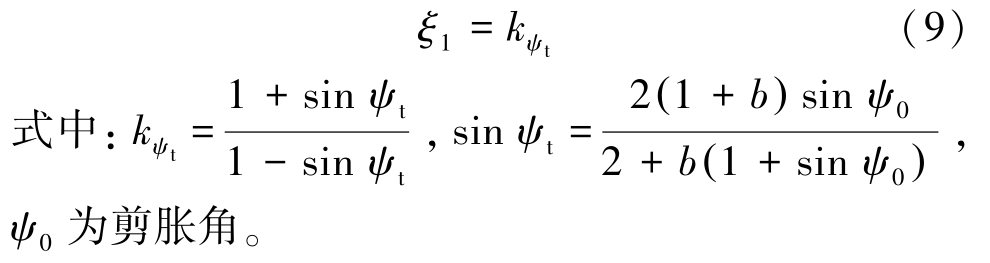
而破碎区扩容系数ξ2 定义为ξ2 =1+μ，μ 介于0.3～0.5 。 因此，一般可取 ξ2 =1.3 ～ 1.5。 岩石应变模型如图2 所示。
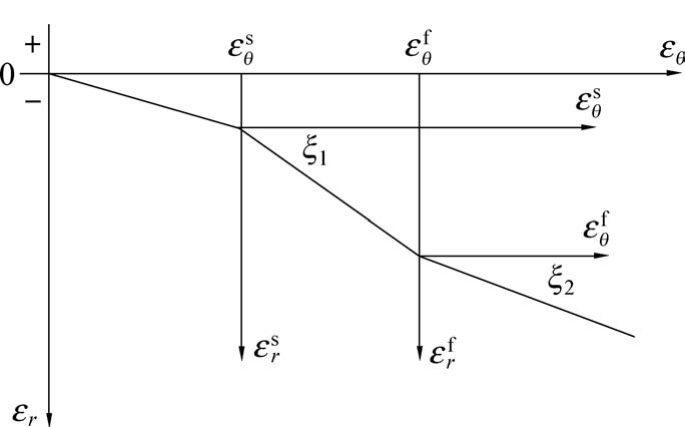
图2 岩石应变模型
Fig.2 Rock strain model
1.4 支护反力
关于弹性区支护反力的存在方式，一直存在一定的争议。 本文采用孙钧院士处理方法，即用虚拟支护阻力
代替支护反力pi ，其中虚拟支护阻力
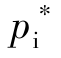是变量，根据文献[8]，可得
式中:p0 为原岩应力，p0=γH，γ 为上覆岩层容重，H为巷道埋深
V 为掘进工作面平均推进速度；
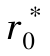为非圆形巷道的当量半径； t 为断面开挖瞬间的起始时间，为一次开挖，取t=1 d。
1.5 开挖卸荷巷道围岩力学模型
软岩巷道开挖后，假定受开挖效应影响的围岩径向范围Rs不大于巷道开挖半径r0 的5 倍，Rf 为破坏区半径，如图3 所示。
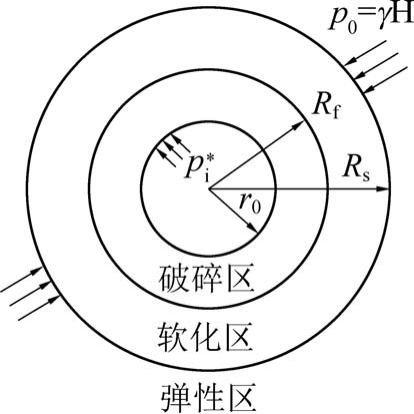
图3 巷道开挖后断面径向力学模型
Fig.3 Radial profile of surrounding rock near excavation face
根据以上假设和基本方程与模型，对卡斯特纳方程进行修正，可得到如式(11)所示的开挖卸荷巷道围岩力学模型为
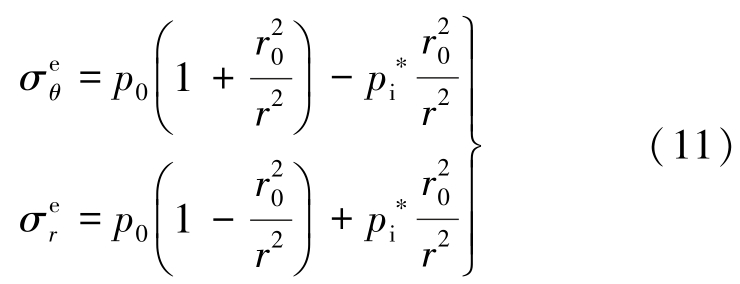
式中
分别为弹性区切向和径向应力；r 为围岩内任意点半径。
1.6 围岩力学承载结构分区
巷道开挖前处于弹性状态，开挖后应力重新分布达到新的力学平衡，在应力重新分布中切向应力变化最明显。 根据切向应力“增加—减小—趋稳”变化趋势，将围岩依次分为浅承载圈、深承载圈和自稳承载圈，并将切向应力集中区定义为主承载圈；同时，考虑剪切破坏是岩石主要的破坏方式，将等效剪应力集中区定义为关键承载圈，如图4 所示。
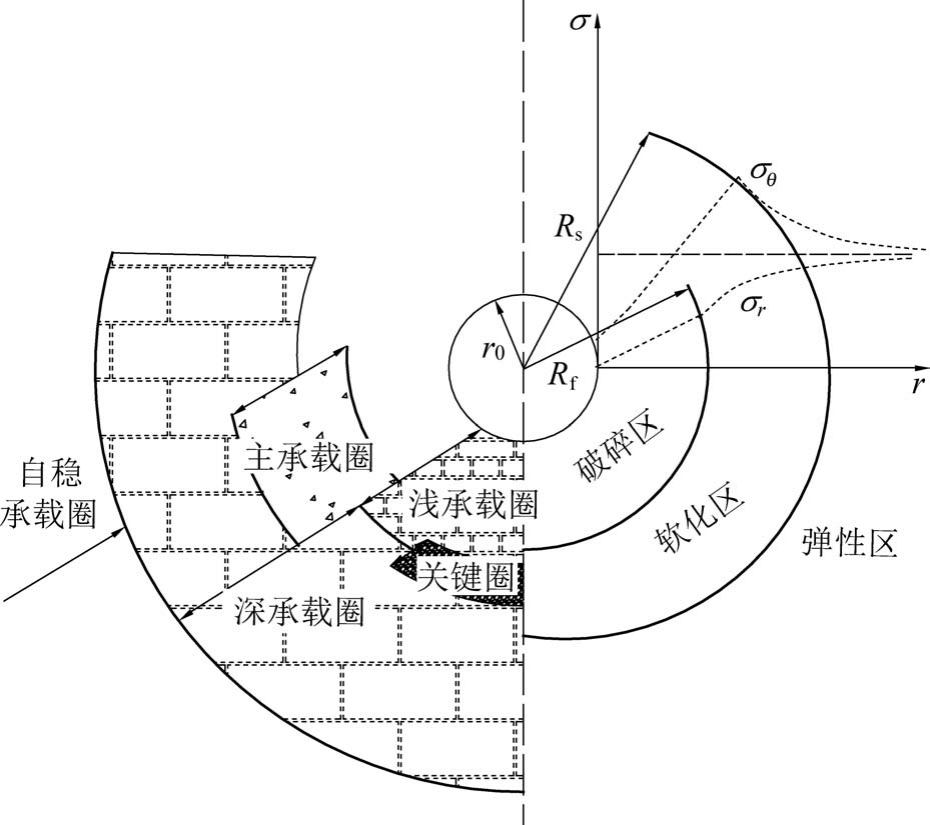
图4 开挖巷道围岩应力承载结构
Fig.4 Mechanical bearing structure of surrounding rock
图4 中浅、深承载圈分别为巷道主动、被动支护区，浅承载圈稳定性较低，是锚杆支护部位，深承载圈锚索补强支护区。 主、关键承载圈影响整个承载结构稳定性，关键承载圈最易破坏点发生在应力峰值点之前，主承载圈承受高应力，转移其承载范围是后期支护主要工作。 在给定环向、轴向、径向三维应力下，可建立等效应力、等效剪应力之间的换算关系式。 在平面应变情况下，根据Levy-Mises 本构关系可知三维应力之间关系为
根据三维流变实验结果和一维蠕变的等时曲线相似的假设，引入有效应力σi 。 在广义平面应变问题中，有σi[16]为
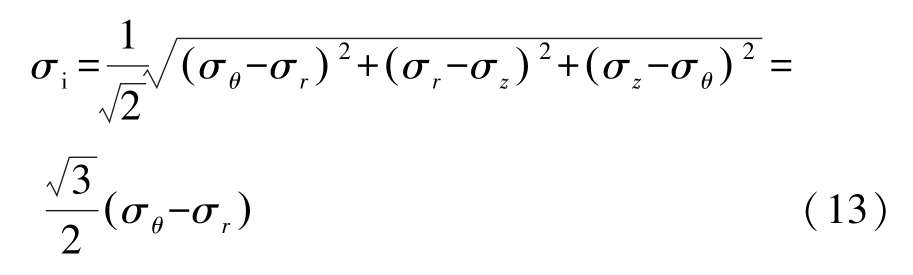
由等效应力与等效剪切应力之间关系，结合式(13)可知复杂应力下等效剪应力表达式为
式中:σi 为有效应力；τi 为等效剪应力。
2 应力场、位移场求解
2.1 围岩屈服应力
根据弹性区的应力解，可得
弹性区径向位移ue 为
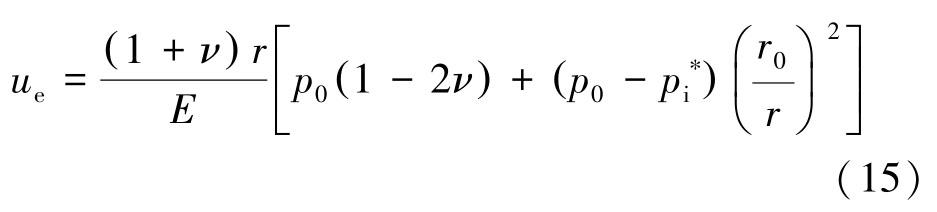
式中:ν 为泊松比；E 为围岩弹性模量。
由于围岩屈服是由于弹性区应力达到屈服应力临界值引起的，所以由式(3)、式(11)联立，可得
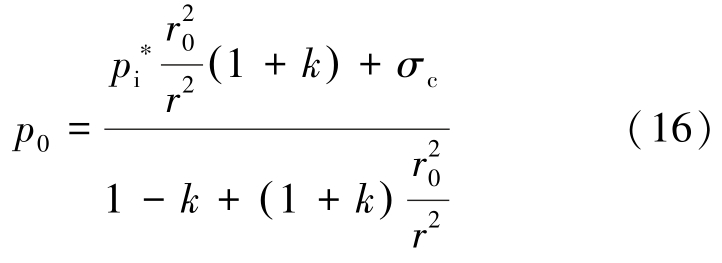
式中:σc 为岩石单轴抗压强度。
巷道围岩在巷道周边r=r0 处开始屈服，其最小值见式(16)，为统一屈服准则下围岩开始屈服时的围岩屈服应力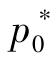
，即
2.2 巷道开挖后围岩位移场
2.2.1 弹性区位移场
根据弹性理论，可知弹性区位移场为
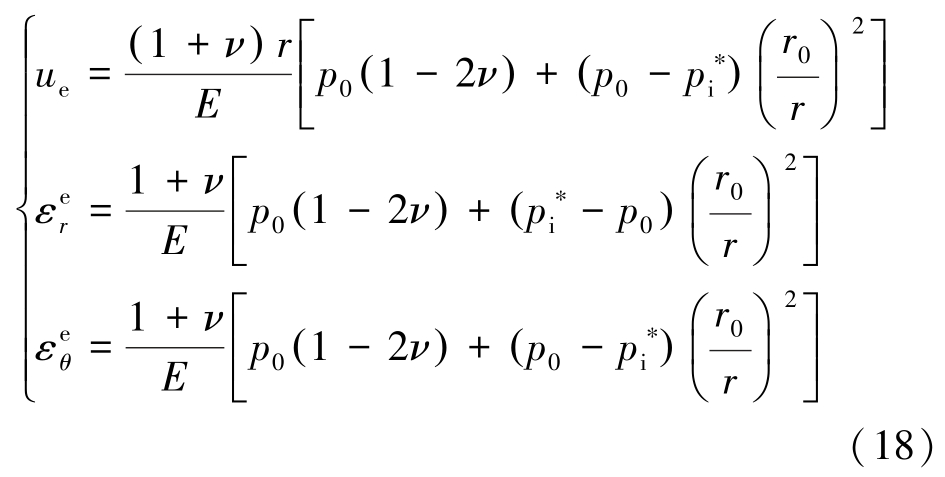
2.2.2 软化区位移场
软化区总应变为弹性极限应变和软化应变增量之和，即
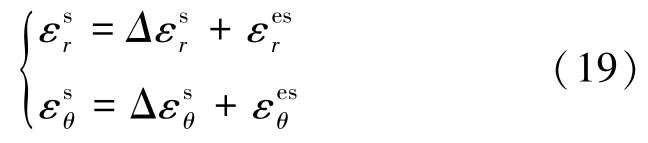
式中
分别为软化区径向、切向应变
分别为弹性区与软化区交界处径向、切向应变。
由式(5)和式(19)可得
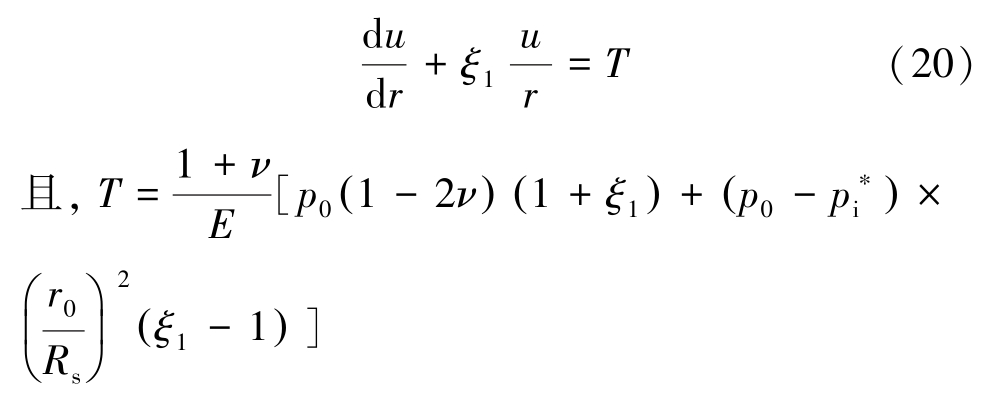
可得软化区位移场参数为
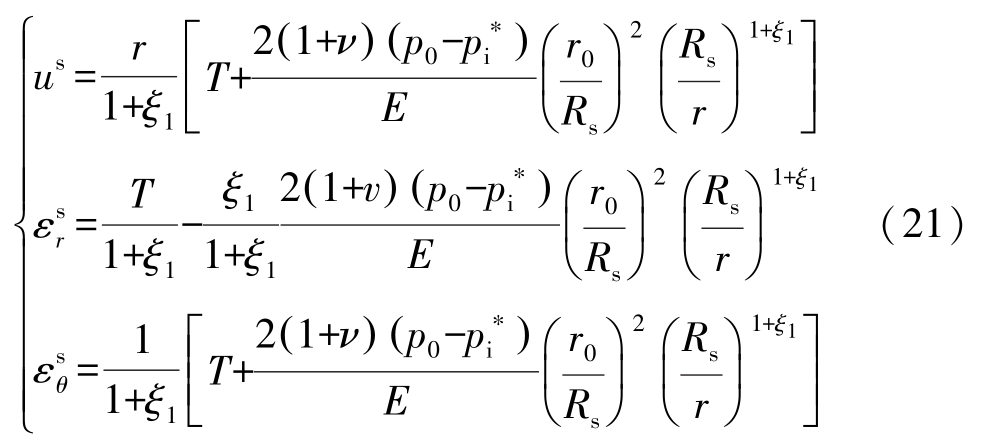
2.2.3 破碎区位移场
同理，得破碎区内总应变为
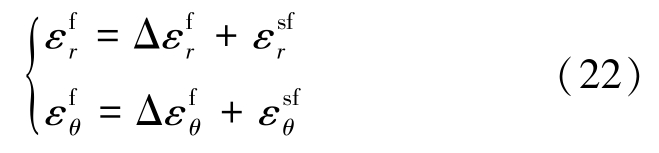
式中
分别为软化区与破碎区交界处径向、切向应变。
根据软化区位移解法，得破碎区位移为
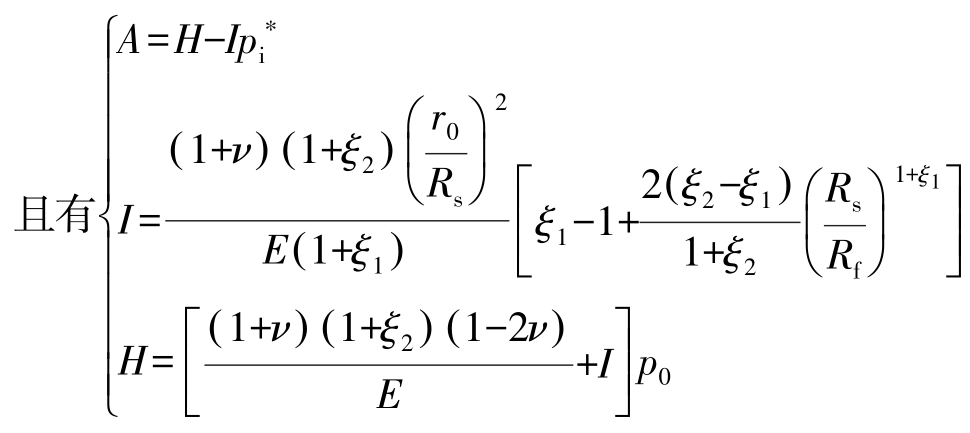
2.3 围岩次生应力场及变形区范围
2.3.1 软化区次生应力场及范围
由边界条件
可知:
由连续条件
可得软化区范围为
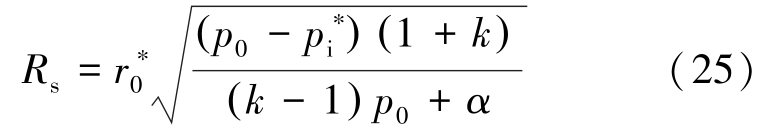
2.3.2 破碎区次生应力场及范围
由边界条件
可知应力为
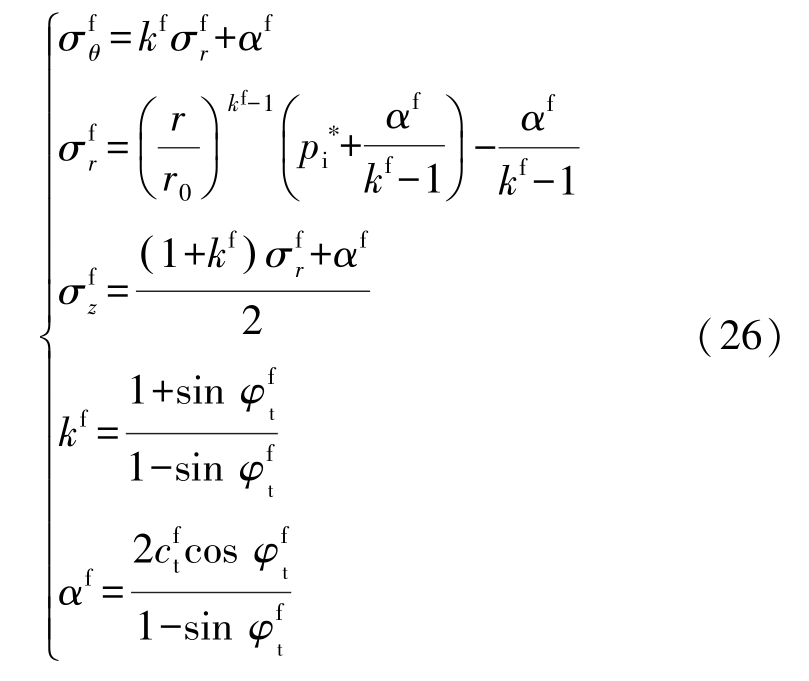
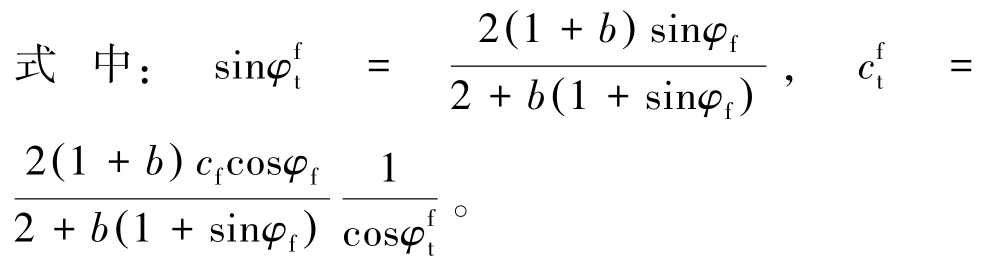
由连续条件 cs = cf 或 φs = φf ，可得
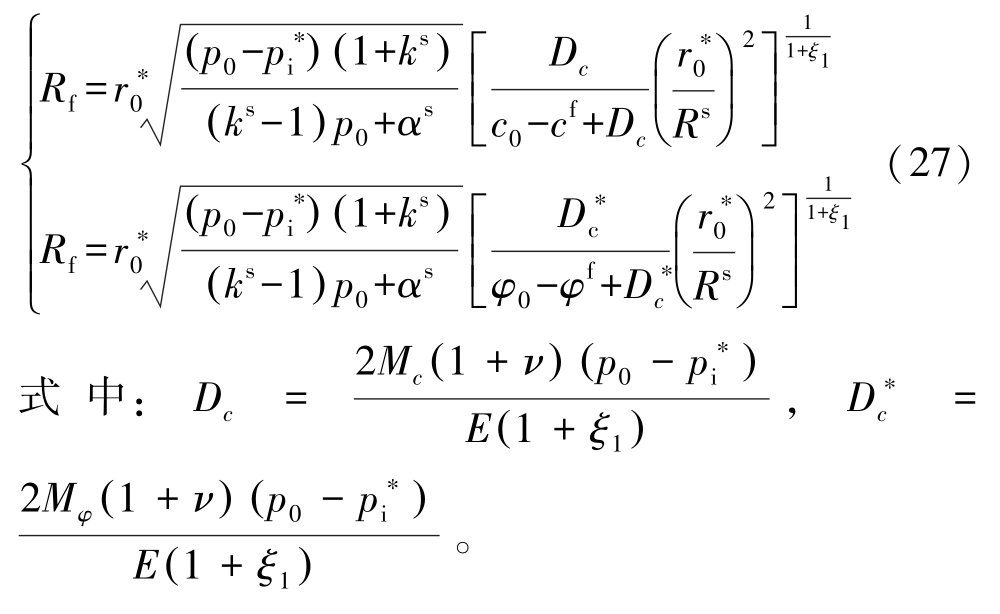
3 软岩巷道开挖围岩力学响应分析
3.1 巷道工程力学参数
某深部软岩巷道围岩为砂质泥岩，平均掘进速度V = 3 m/d。 埋深Η = 952 m，初始黏聚力 c0 =3.5 ΜΡa、内摩擦角 φ0 = 25°，剪胀角 ψ0 = 10°，抗剪强度τs = 15.2 ΜΡa，RMTS 三轴压缩试验获得塑性应变增量平均值
黏聚力、内摩擦角增量的平均值Δc = 0.36 ΜΡa、Δφ = 1.24°，黏聚力、内摩擦角软化模量Mc = 375 ΜΡa、Mφ = 1 385°。
3.2 围岩屈服应力影响因素及分析
3.2.1 围岩力学性质
围岩物理力学性质对巷道开挖后围岩的屈服破坏应力有影响。 依据式(17)和第3.1 中相关的工程力学参数，可以得到不同破坏模型下围岩屈服应力随黏聚力的变化如图5 所示。 同样，可以得到不同破坏模型下围岩屈服应力随内摩擦角的变化如图6所示。
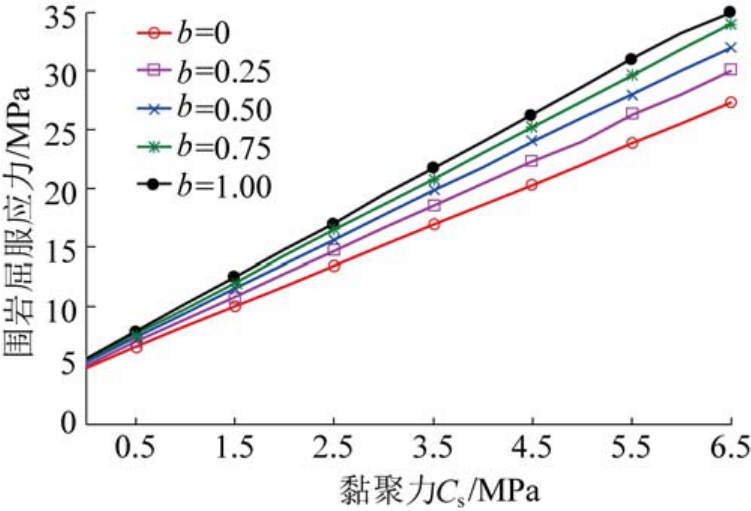
图5 屈服应力受黏聚力影响
Fig.5 Yield stress influenced by cohesion
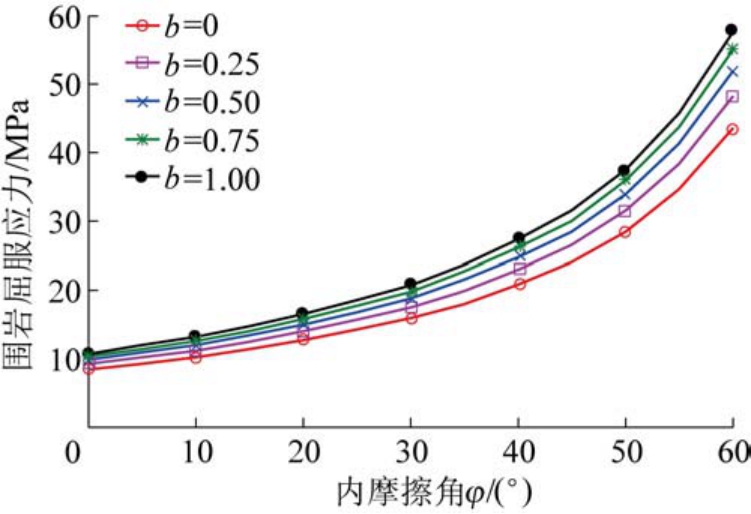
图6 屈服应力受内摩擦角影响
Fig.6 Yield stress influenced by internal friction angle
从图5 和图6 可以看出，巷道围岩屈服应力随着岩石黏聚力和内摩擦角的增大而增大。 说明，黏聚力和内摩擦角小的岩石在同样开挖速度和开挖断面的影响下，越容易达到屈服应力被破坏。
3.2.2 掘进速度
依据式(17)和第3.1 中相关的工程力学参数，可以得到围岩屈服应力随巷道掘进速度的影响如图7 所示。
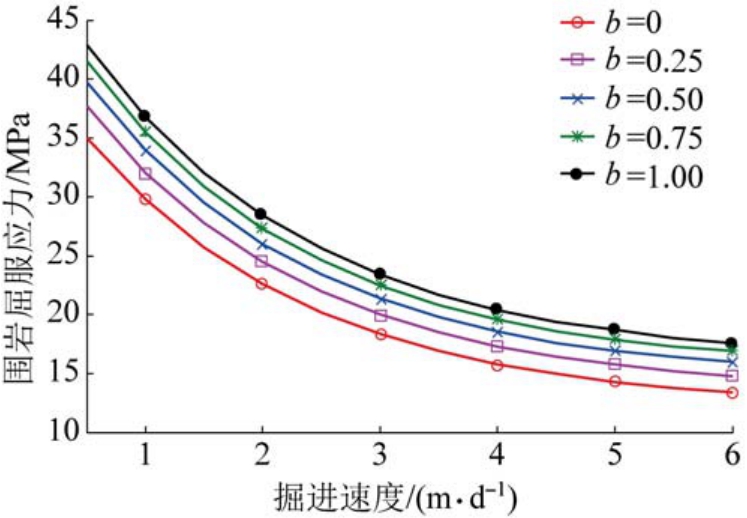
图7 屈服应力受掘进速度影响
Fig.7 Yield stress influenced by excavation speed
由图7 可以看出，围岩屈服应力随着掘进速度的增加而呈非线性的降低，掘进速度越快，围岩越容易达到屈服应力发生破坏。 因此，实际软岩工程中应控制掘进速度，防止因掘进速度过快导致围岩快速达到屈服而影响巷道的稳定性。
从图5—图7 还可以看出，选用不同的岩石破坏准则对岩石屈服应力的计算也有一定的影响，采用广义双剪准则解计算得到的岩石屈服应力最大，Mohr-Coulomb 准则最小。 因而，为了确保巷道开挖工程的安全性和可靠性，建议选择广义双剪准则进行计算。
3.3 围岩破裂区、软化区影响因素及分析
3.3.1 黏聚力、黏聚力软化模量及剪胀角
依据式(25)、式(27)和第3.1 中相关的工程力学参数，可得到软化区范围随黏聚力变化以及黏聚力软化模量分别为200、400 和600 MPa 时碎裂区范围随黏聚力变化的曲线如图8 所示。
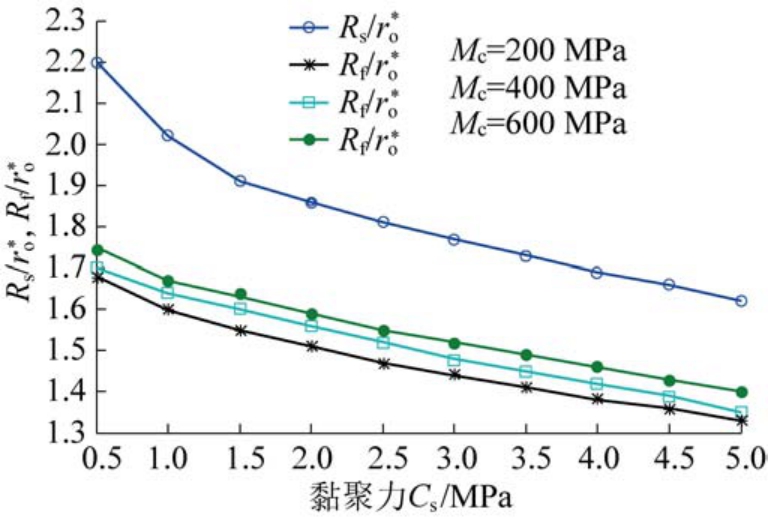
图8 黏聚力及软化模量对软化、破碎区范围影响
Fig.8 Softening and fractured scope vs.cohesion and soften modulus
依据式(25)、式(27)和第3.1 中相关的工程力学参数，可得到软化区范围随黏聚力变化以及剪胀角分别为10°、15°和20°时碎裂区范围随黏聚力变化的曲线如图9 所示。
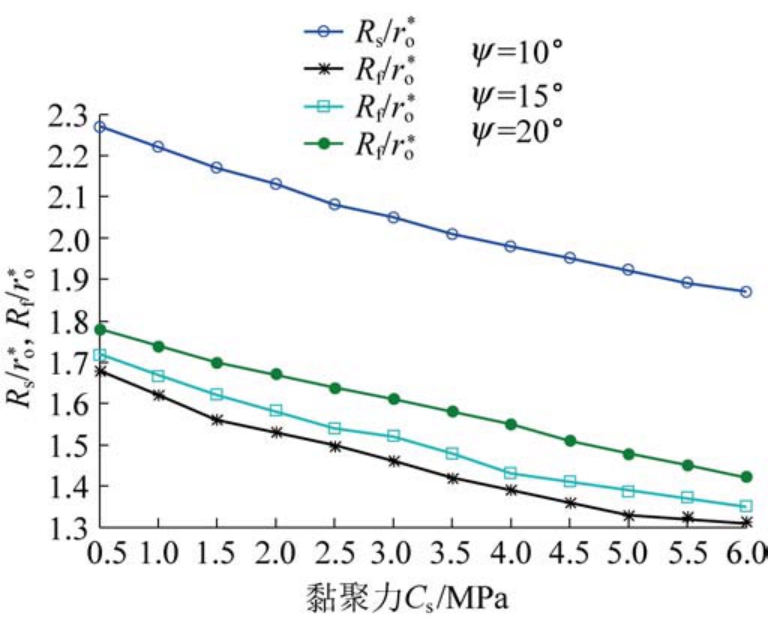
图9 黏聚力和剪胀角对软化区、破碎区范围影响
Fig.9 Softening and fractured scope vs.cohesion and dilation angle
由图8、图9 可知，随着黏聚力增大围岩软化区、破碎区范围减小，初始黏聚力大的软岩巷道其破碎区和软化区范围小，有利于巷道稳定，巷道需要支护的深度小。 在黏聚力一定的情况下，黏聚力软化模量越小或者剪胀角越小，破碎区的范围越小。 巷道开挖后，应及时支护，避免黏聚力软化增加和剪胀角增大导致后期需要支护的巷道范围扩大。
2.3.2 剪胀角、掘进速度和支护参数
依据式(25)、式(27)和第3.1 中相关的工程力学参数，考虑锚杆支护间距×排距分别为1 600 mm×1 600 mm 和800 mm×800 mm，可得到掘进速度分别为2.5、3.5 和4.5 m/d 时，碎裂区范围随剪胀角的变化关系如图10 所示。
由图10 可以看出:①在同样的支护条件和掘进速度下，碎裂区的范围随着剪胀角的增大而增加；②在同样的支护条件和剪胀角下，碎裂区的范围随着掘进速度的增大而增加；③在同样的掘进速度和剪胀角下，裂区的范围随着锚杆支护间排距的减小而减小。 可见，对于软岩巷道而言，为了维护巷道的稳定性缩小支护范围，要控制一定的掘进速度，同时要考虑加密锚杆支护。
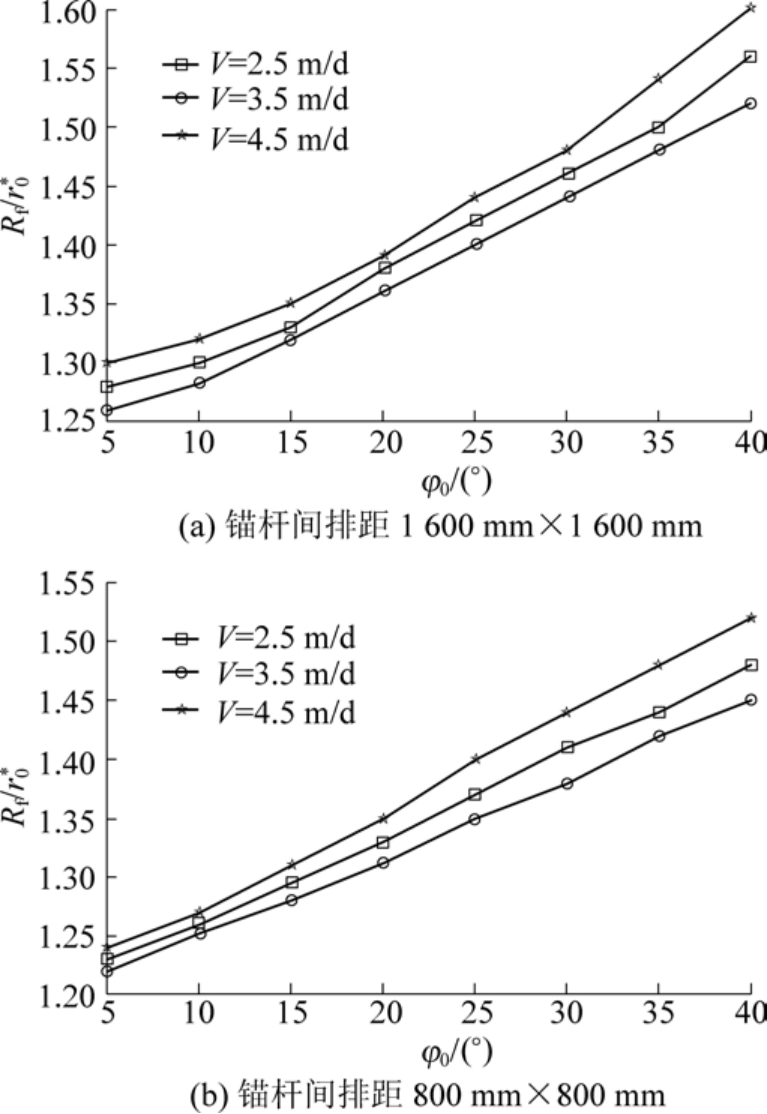
图10 不同掘进速度下破碎区范围随剪胀角变化
Fig.10 Variation of fracture zone range with shear angle under different driving speeds
3.4 围岩软化程度对承载结构的影响
由图5 中围岩力学承载结构划分方法，结合式(13)、式(22)、式(24)中关于弹性区、软化区、破碎区应力解析解，依据第3.1 节相关工程力学参数，可得到岩性软化程度(分为弱软化、中等软化和强软化3 种情况)对围岩力学结构中“主-关键”承载圈的影响见表1。
由表1 可以看出，围岩软化程度对巷道开挖后的承载结构有较大的影响。 随着围岩软化程度增加:①主承载圈和关键承载圈向巷道深部转移且承载范围增大，相比于弱软化围岩，强软化围岩的主承载圈、关键承载圈范围分别增大62.5%和58.62%；②切向应力、轴向应力峰值位置同样向巷道深部转移且应力峰值也随之增大，若弱软化围岩转变为强软化，切向应力、轴向应力峰值分别增大16.67%和31.46%；③关键承载圈中最易失稳点往巷道深部转移，④等效剪应力随之增大。 因此，在软岩巷道开挖工程中，要防止岩石软化导致承载圈承载力增大并向深部转移而导致需要支护的范围增大，支护难度增加。
表1 不同软化程度巷道围岩主承载圈与关键承载圈特征
Table 1 Characteristics of main bearing circles and key bearing circles of surrounding rock under different degrees of softening
围岩软化程度主承载圈关键承载圈范围 应力集中点位置切向应力集中系数轴向应力集中系数 范围 最易失稳点 等效剪应力τi，max/MPa弱软化 1.44r0 ～1.68r0 1.510r0 1.50 0.89 1.48r0 ～1.65r0 1.495r0 15.30中等软化 1.56r0 ～1.92r0 1.605r0 1.68 1.05 1.58r0 ～1.82r0 1.595r0 16.12强软化 1.59r0 ～1.98r0 1.730r0 1.75 1.17 1.61r0 ～1.90r0 1.710r0 16.75
4 结 论
考虑巷道开挖卸荷效应、软岩本构模型影响，通过理论公式推导，给出巷道开挖后不同强度准则下围岩稳定性指标表达式，再根据次生应力场分布规律，将围岩力学承载结构划分为“深-浅-主-关键-自稳”承载圈，得到研究结论如下:
1)软岩巷道开挖后的围岩屈服应力受围岩初始黏聚力、内摩擦角和巷道开挖速度等因素的影响，围岩初始黏聚力、内摩擦角越小，掘进速度越大，围岩越容易达到屈服应力发生破坏。 选用不同的岩石破坏准则对岩石屈服应力的计算也有一定的影响，采用广义双剪准则解计算得到的岩石屈服应力最大，其计算结果偏安全性。
2)围岩破裂区、软化区影响范围受黏聚力、黏聚力软化模量、剪胀角、掘进速度和支护参数等诸多因素影响，为便于巷道稳定，减小巷道支护深度，应及时采取措施避免黏聚力软化增加和剪胀角增大，同时要控制掘进速度，选择合适的低密度锚杆支护。
3)巷道开挖后形成的围岩承载结构受围岩软化程度影响，随着围岩软化程度的增加，主承载圈和关键承载圈的范围、径向应力和轴向应力的峰值随之增大，且向巷道深部转移，软岩巷道需要支护的范围增大，支护难度增加。
[1]文志杰，卢建宇，肖庆华，等.软岩回采巷道底臌破坏机制与支护技术[J].煤炭学报， 2019，44(7):1991-1999.WEN Zhijie，LU Jianyu，XIAO Qinghua，et al.Failure mechanism of floor heave and supporting technology of soft rockroadway[J].Journal of China Coal Society，2019，44(7):1991-1999.
[2]马资敏，郭志飚，陈上元，朱 盛，王 进.深部中厚煤层切顶留巷围岩变形规律与控制研究[J].煤炭科学技术， 2018， 46(2):112-118，242.MA Zimin， GUO Zhibiao， CHEN Shangyuan， ZHUSheng，WANGJin.Study on deformation law and control of surrounding rock in roofcutting gateway retained along goaf in deep medium thick seam[J].Coal Science and Technology， 2018， 46(2):112-118，242.
[3]王卫军，袁 超，余伟健，等.深部大变形巷道围岩稳定性控制方法研究[J].煤炭学报，2016，41(12):2921-2931.WANG Weijun，YUAN Chao，YU Weijian， et al.Stability control method of surrounding rock in deep roadway with large deformation[J].Journal of China Coal Society， 2016， 41(12):2921-2931.
[4]张官禹，赵 龙，尚玉强.软岩巷道底鼓成因分析及关键控制技术研究[J].煤炭科学技术，2019，47(11):63-67.ZHANG Guanyu，ZHAO Long，SHANG Yuqiang.Study on key control technology of floor heave in soft rock roadway[J].Coal Science and Technology， 2019， 47(11):63-67.
[5]罗先启，舒茂修.岩爆的动力断裂判据—D 判据[J].中国地质灾害与防治学报，1996，7(2):1-5.LUO Xianqi， SHU Maoxiu.Dynamic fracture criterion of rock burst:D Criterion[J].The Chinese Journal Of Geological Hazard And Control，1996，7(2):1-5.
[6]FAKHIMI A， CARVALHO F， ISHIDA T， et al.Simulation of failure around a circular opening in rock[J].International Journal of Rock Mechanics and Mining Sciences，2002，39(4):507-515.
[7]MARTIN C D，KAISER P K，CHRISTIANSSON R.Stress instability and design of underground excavations[J].International Journal of Rock Mechanics and Mining Sciences， 2003， 40 (7/8):1027-1047.
[8]孙 钧.岩石流变力学及其工程应用研究的若干进展[J].岩石力学与工程学报，2007，26(6):1081-1106.SUN Jun.Rock rheological mechanics and its advance in engineering applications[J].Chinese Journal of Rock Mechanics and Engineering，2007，26(6):1081-1106.
[9]侯公羽，牛晓松.基于Levy-Mises 本构关系及Hoek-Brown 屈服准则的轴对称圆巷理想弹塑性解[J].岩石力学与工程学报，2010，29(4):765-777.HOU Gongyu，NIU Xiao-song.Perfect elastro-plastic solution of axi-symmetric cylindrical cavity based on Levy-Mises constitutive relation and Hoek-Brown failure criterion[J].Chinese Journal of Rock Mechanics and Engineering，2010，29(4):765-777.
[10]SENENTS， MOLLON G， JIMENEZ R.Tunnel face stability in heavily fractured rock masses that follow the Hoek-Brown failure criterion[J].International Journal of Rock Mechanics and Mining Sciences，2013，60:440-451
[11]彭 瑞，孟祥瑞，赵光明，等.基于增量型本构关系的深埋巷道开挖面附近围岩统一解[J].中国矿业大学学报， 2015，44(3):444-452.PENG Rui， MENG Xiangrui， ZHAO Guangming， et al.Surrounding rock unified solution near deep-buried roadway excavation workface considering incremental constitutive relationship[J].Journal of China University of Mining & Technology，2015，44(3):444-452.
[12]董方庭，宋宏伟，郭志宏.巷道围岩松动圈支护理论[J].煤炭学报， 1994， 19(1):31-32.DONG Fangting，SONG Hongwei，GUO Zhihong.Roadway support theory based on broken rock zone[J].Journal of China Coal Society，1994，19(1):31-32.
[13]康红普.巷道围岩的承载圈分析[J].岩土力学，1996，17(4):84-89.KANG Hongpu.Bearing ring analysis of roadway surrounding rock[J].Rock and Soil Mechanics，1996，17(4):84-89.
[14]余伟健，高 谦，朱川曲.深部软弱围岩叠加拱承载体强度理论研究及应用[J].岩石力学与工程学报，2010，29(10):2134-2142.YU Weijian，GAO Qian， ZHU Chuanqu.Study of strength theory and application of overlap arch bearing body for deep soft surrounding rock[J].Chinese Journal of Rock Mechanics and Engineering，2006，25(7):1304-1308.
[15]赵光明，宋顺成，杨显杰.基于增量本构关系弹塑性分析的无网格伽辽金法[J].中国矿业大学学报，2005，34(4):105-109.ZHAO Guangming，SONG Shunchen，YANG Xianjie.Elementfree Galerkin Method for elastic-plastic analysis based on incremental constitutive equations[J].Journal of China University of Mining & Technology，2005，34 (4):105-109.
[16]陆银龙，王连国，杨 峰，等.软弱岩石峰后应变软化力学特性研究[J].岩石力学与工程学报，2010，29(3):640-648.LU Yinlong， WANG Lianguo， YANG Feng， et al.Post-peak strain softening mechanical properties of weak rock[J].Chinese Journal of Rock Mechanics and Engineering， 2010，29(3):640-648.
