0 引 言
近年来我国城镇建设迅猛发展,建设用地日趋紧张,特别是对于煤炭资源矿业型城市,由于受地下采煤塌陷影响,一些工业与民用建筑物不得不建在采动(空)区之上[1-2]。在采煤塌陷区进行建筑结构设计时,除了考虑常规的荷载和作用之外,还应考虑采动地表变形对于结构的不利影响,即受采动影响的建筑结构必须同时考虑常规荷载和采动作用的双重设计要求。我国从20世纪70年代开始就开展了抗采动变形建筑结构的理论研究和实践工作,陆续建设了低层、多层浅基础型式的抗变形建筑。滕永海等[3-6]研究了采煤塌陷区地基稳定性评价方法和地表移动变形计算方法,通过采取采空区注浆、设置变形缝、加强基础及上部结构强度等综合抗变形技术措施,已在平顶山、开滦、焦作等矿区成功建设了大面积的住宅小区和工业厂房;张俊英等[7-9]对于砖混结构和框架结构的抗变形理论计算方法进行了研究,内容包括煤矸石地基处理技术、滑动层作用分析和上部结构受力体系研究等;夏军武等[10-11]对于采动地基变形、基础(独立基础及条形基础)和上部结构的协同作用机理进行了试验研究,建立了协同作用的力学模型,推导并得出了求解建筑物附加内力、附加变形和地基附加反力的计算公式。上述学者在采动区建筑地基稳定性评价和抗变形设计方面取得了一定理论成果和进行了成功的建筑实践,但其大多是针对采用浅基础的建筑进行的研究,对于受采动作用影响下深基础(桩基础)的抗变形设计理论和方法还需要进一步研究。
随着采动区建筑层数和荷载的增加,为了满足地基承载力和地基变形的要求,建筑物基础也要求相应的采用深基础的结构型式。其中,在高层、中高层民用建筑及荷载较大的工业建筑中,钢筋混凝土灌注桩基础是普遍采用的桩基形式。灌注桩的常规设计主要是根据桩顶荷载(抗震设计时考虑地震作用)进行基桩竖向承载力、水平承载力、桩身抗压承载力和桩身受拉承载力等计算,同时满足有关构造要求,在特殊工程地质条件下还应当考虑软弱下卧层、负摩阻力等的影响[12]。桩的承载力主要与桩身截面尺寸、材料等级、桩周和桩端土性参数、桩顶嵌固形式、桩端支撑条件以及桩身纵向配筋率等有关。
目前,桩基的常规设计理论和方法比较成熟,但在采动区进行桩基设计时尚应考虑采动区的采动变形影响,而在各种采动因素中以地基土体水平变形影响为最主要[13-14]。笔者仅对在桩顶水平力(包括集中力和弯矩)和地基土体水平变形作用下桩的受力特性进行了分析,详细推导了在水平荷载作用下桩的挠曲变形微分方程,将地基土体位移转化为桩顶集中力并与桩顶常规水平力相叠加作为桩顶荷载效应进行桩身承载力计算,为采动区基桩在综合荷载和作用下的设计计算提供了一种思路和方法。
1 基桩受力分析
1.1 水平荷载下桩的工作特性
基桩不仅能够承受竖向荷载,而且能够通过抗弯和抗剪来承担一定的水平荷载。桩基所受水平力一般由地震、风、机械振动等所引起,其对桩基的水平作用力应考虑2个方向的影响。桩顶水平荷载包括水平集中力和弯矩。在水平荷载作用下桩与土相互作用,桩身的水平位移与土的变形相协调。当桩身发生水平变位时,桩周土发生相应的变形而产生抗力。桩的水平承载力即与桩周土体水平抗力大小密切相关,而桩周土体水平抗力大小又与桩的截面尺寸、桩顶约束条件、桩端支承条件、桩周土质条件以及桩的入土深度等因素有关[15-17]。
据基桩的换算深度可将桩分为刚性基桩(αh≤2.5,α为基桩的水平变形系数)和柔性基桩(αh>2.5)。刚性基桩入土较浅,桩的刚度远大于土层的刚度,桩周土体水平抗力较低,桩的水平承载力主要由桩的水平位移和倾斜控制。柔性桩在水平荷载作用下,将形成一段嵌固的地基梁,并在桩身不同深度处产生不同的弯矩值和剪力值。桩身在水平荷载作用下发生挠曲变形,承载力一般由桩顶水平位移和桩身最大弯矩所控制。
水平荷载作用下桩基计算有地基反力系数法、弹性理论法、极限平衡法和数值计算法等。其中,地基反力系数法是我国目前广泛采用的方法之一。地基水平抗力系数有多种计算方法,常用的为“m”法。“m”法符合Winkler地基模型,该模型把桩周土离散为一个个单独作用的弹簧,某一弹簧仅发生与该弹簧作用力成正比的压缩而和其他弹簧无关[18-19]。
当桩受水平荷载作用后,在桩身下某一深度z处的桩侧土水平抗力σx与该点水平位移x成正比,且地基系数kh随深度z呈线性增长,即
σx=khx
(1)
kh=mz
(2)
式中:m为地基土水平抗力系数的比例系数,kN/m4。
1.2 基桩挠曲微分方程
柔性基桩在水平力(水平集中力和弯矩)作用下,在地基土中相应产生抗力,基桩发生挠曲变形。以变形前桩顶形心O为原点,建立坐标系,水平方向为x轴,竖向为z轴,如图1所示。沿桩身取微段dz进行受力分析,各力正方向如图1所标示。图1中,Mz、Vz、Nz分别为桩顶下z处的弯矩、剪力和轴力,dM、dV、dN分别为弯矩、剪力和轴力的增量,pz为线性分布地基土抗力。
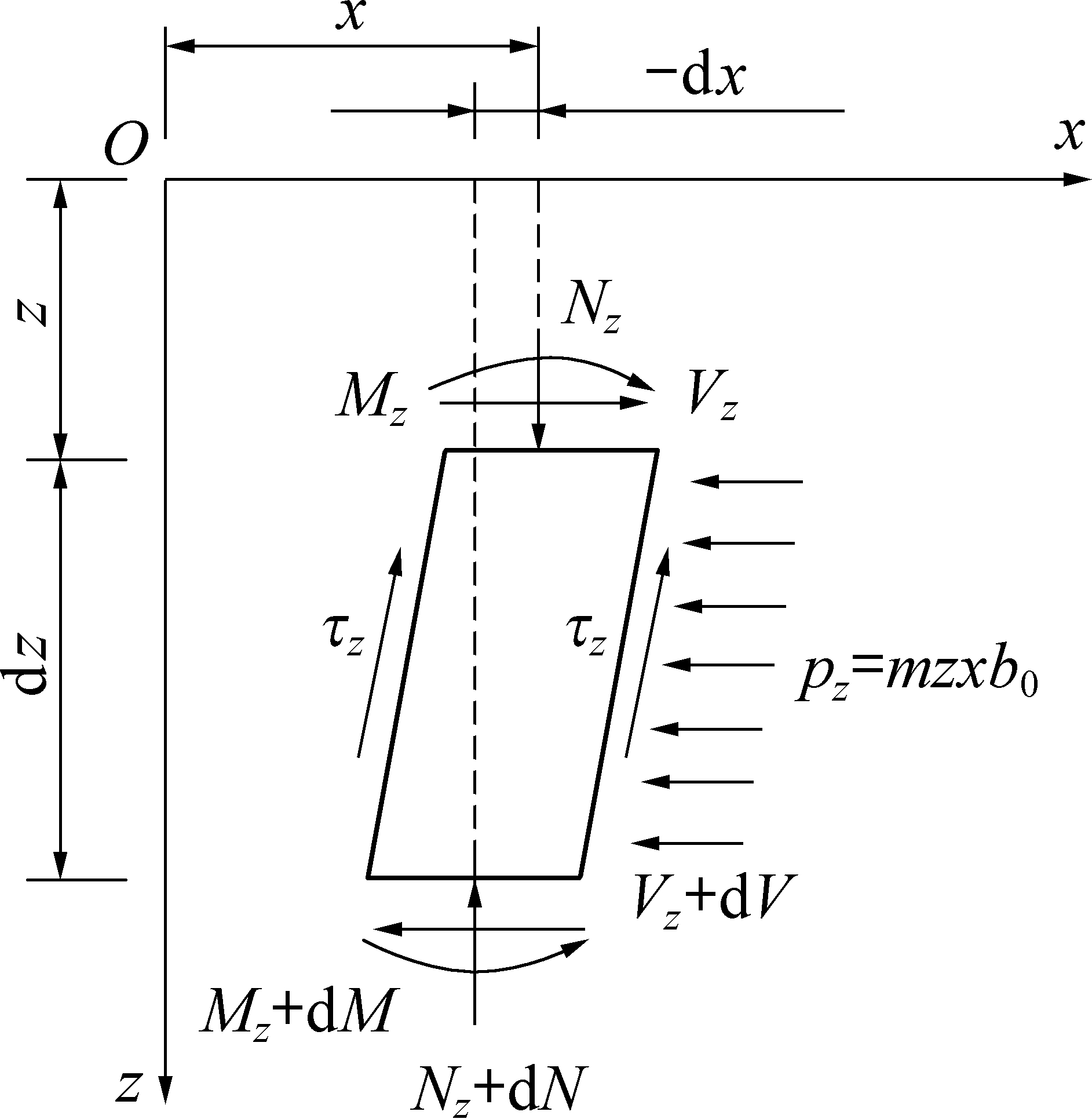
图1 微段受力分析
Fig.1 Stress analysis of micro segment
根据弹性地基梁理论建立桩的挠曲微分方程,推导过程如下:
以微段下端截面中点为矩心建立力矩平衡微分方程,其中,轴力Nz对矩心取矩时力臂应取-dx。沿微段水平方向建立力平衡方程,即
(Mz+dMz)-Mz-Nz(-dx)-Vzdz+pz(dz)2/2=0
(3)
Vz-(Vz+dV)-pzdz=0
(4)
式(3)略去二阶微量后,得
dMz/dz+Nzdx/dz-Vz=0
(5)
对式(5)两侧再次求导有
(6)
式(4)整理后得
![]() =-pz
=-pz
(7)
由高等数学知识知,曲率K与曲率半径ρ(z)成反比,计算式为
(8)
略去二阶微量后,得
K=1/ρ(z)=±d2x/dz2
(9)
并且曲率正负号与所建立坐标系有关。
由材料力学知识可知,桩发生挠曲变形时曲率与弯矩之间存在如下关系为
K=1/ρ(z)=M/EI
(10)
式中:EI为桩的抗弯刚度。
将式 (9)代入式(10)得
d2x/dz2=±M/EI
(11)
将式(7)和式(11)代入式(6),按图1所示坐标系,式(11)右侧应取“+”,可得
(12)
且pz=mzxb0
式中:b0为桩的计算宽度。
由于Nz作用影响很小,忽略Nzd2x/dz2项的影响,式(12)简化整理后
d4x/dz4+α5zx=0
(13)
式中:α为桩的水平变形系数,![]()
采用幂级数求解微分方程式(13),可得在桩长为L的桩顶水平力H0和桩顶弯矩M0作用下桩身深度z处的位移、弯矩和剪力表达式(系数Ax、Bx、AM、BM、AQ、BQ可查有关手册得到[20])分别见式(14)—式(16)。桩身的位移xz、弯矩Mz、剪力Vz和水平抗力σx沿深度的典型分布曲线如图2所示。
位移:![]()
(14)
弯矩:![]()
(15)
剪力:
Vz=H0AQ+αM0BQ
(16)
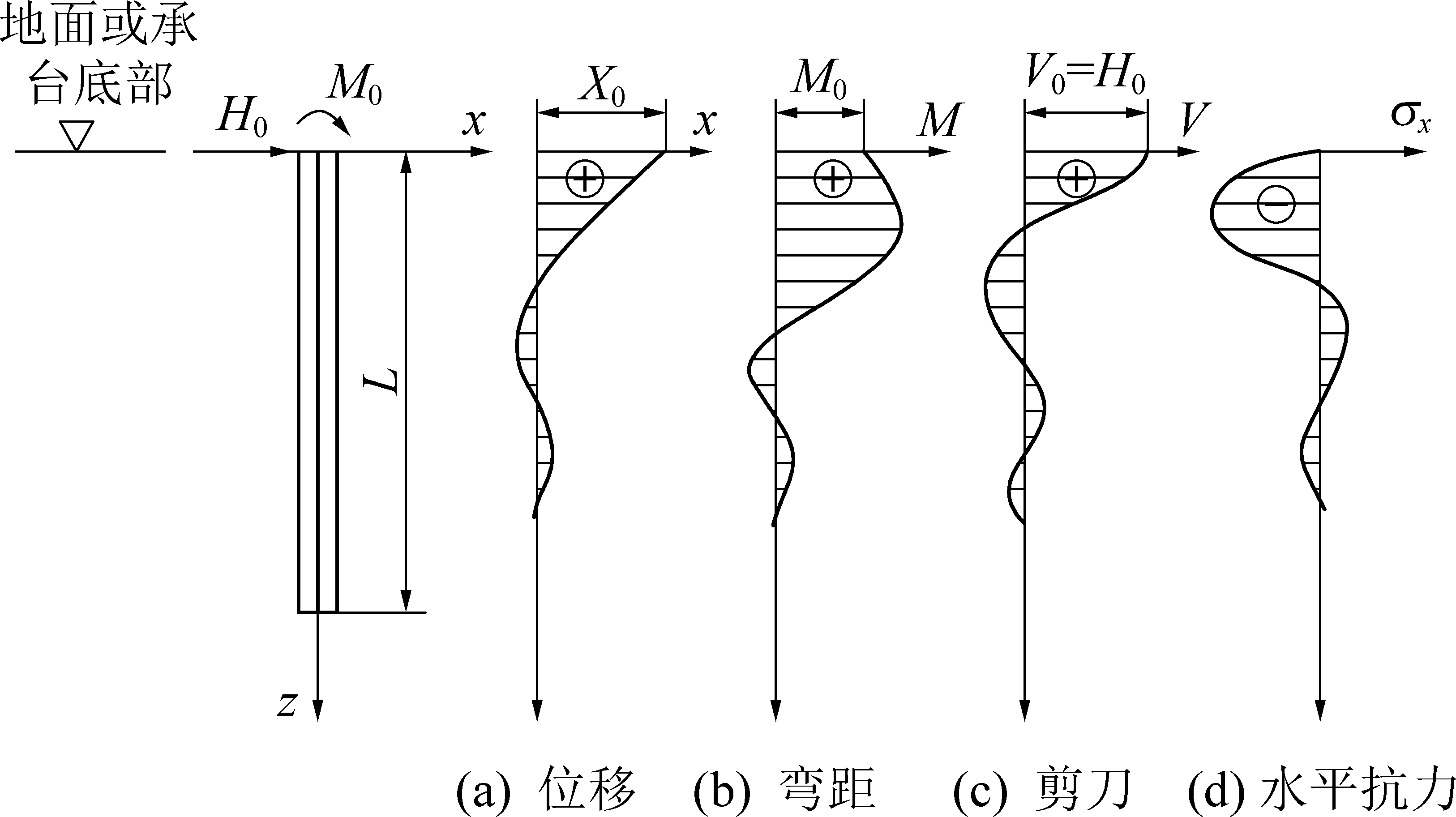
X0—桩顶水平位移;V0—桩顶剪力
图2 水平荷载作用下桩的水平位移及内力
Fig.2 Horizontal displacement and internal force diagram of pile under horizontal load
桩身最大弯矩一般位于桩顶下一定深度,桩身最大弯矩Mmax=CMM0,CM为桩身最大弯矩系数,可查表获得。
1.3 地表水平变形作用下基桩受力特性
在采动影响下地基土体发生水平移动,水平移动引起水平变形(拉伸或压缩)。地基土体水平移动所引起的水平变形是加在桩上最重要的作用力。以拉伸水平变形为例,拉伸水平变形作用下桩基土体水平移动方向及大小如图3所示。对于建筑物的某个独立单元,距该单元对称轴线距离为d的任意一点的地基土体的水平位移Δld是个变量,按式(17)进行计算[21]。
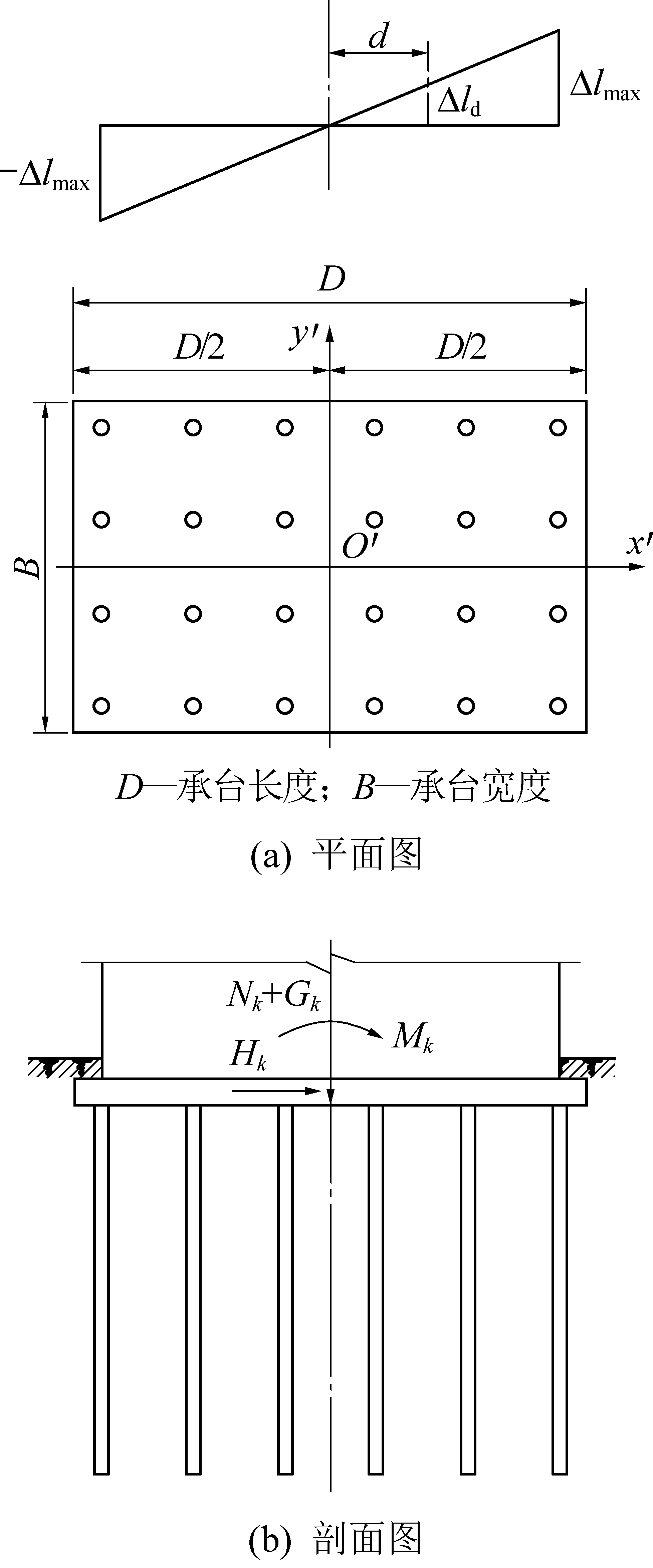
图3 拉伸变形作用下地基土体位移
Fig.3 Displacement of foundation soil under tensile deformation
Δld=m′nεd
(17)
其中,m′为工作条件系数,单元长度大于30 m时,m′=0.7;单元长度为15~30 m时,m′=0.85;单元长度小于15 m时,m′=1;n为超载系数,取1.2;ε为建筑物所在地段内预测的地表最大变形值,并取建筑物一个单元长度内的水平变形为一个常量;d为计算点距建筑对称轴线的距离。
由图3可见,基桩距单元对称轴线越远所承受的土体水平位移的作用力越大,同时,引起的桩中的内力也越大。钢筋混凝土钻孔灌注桩桩顶一般嵌入承台深度较浅,桩顶钢筋仅将主筋深入承台或筏板,很难完成弯矩的传递,因此受力状态类似铰接。在水平力作用下的基桩桩身属于钢筋混凝土受弯构件,需要混凝土和纵向钢筋一起受力才能完成弯矩的传递。
采动区内的基桩设计应遵循的基本原则是尽可能减少桩把水平位移引起的附加内力传递给承台。当建筑单体平面尺寸较长时,可通过设置变形缝将其划分成长度较短单元的方法来减少地基土体的设计移动量。同时,应尽量采用桩顶与承台的柔性嵌固方案,即将桩顶与承台连接处设置成铰接。同时,在承台底与地基土之间设置滑动层可以有效减少地基土体传递给承台的摩擦力,从而减少了承台及上部结构的附加应力。
根据桩顶与承台连接形式不同,桩顶水平位移容许值也不同。当桩顶与承台刚接时,桩顶水平位移容许值为20 mm。当桩顶与承台铰接时,桩顶水平位移容许值为50 mm,另当承台底部设置滑动层时为80 mm[22]。
采动区桩基地基土体在拉伸或压缩水平变形作用下,使基桩相对地基土体产生位移,从而在桩身产生内力。因群桩最外边缘桩所受土体水平作用力最大,故可取群桩最外边缘桩的地基土体移动量作为设计依据。在采动区进行基桩设计时应考虑常规水平力和采动地基土体水平移动下桩基作用力相叠加作为最不利组合进行设计。将地基土体最大位移Δlmax代入式(14),并令M0=0,即可将土体位移转化为等效的桩顶水平集中力为
H′0=Δlmaxα3EI/Ax
(18)
2 基桩桩顶作用效应及承载力
2.1 水平力作用下桩顶作用效应计算
一般建筑物和受常规水平力的建筑群桩基础,其基桩桩顶所受水平力和弯矩可按如下公式进行计算。承台底所受总水平力和弯矩按平均分配给各基桩顶进行考虑。
Hi,k=Hk/n
(19)
Mi,k=Mk/n
(20)
式中:Hk为荷载效应标准组合下,作用于承台底面的水平力;Hi,k为荷载效应标准组合下,作用于第i基桩的水平力;Mk为荷载效应标准组合下,作用于承台底面的弯矩;Mi,k为荷载效应标准组合下,作用于第i基桩的弯矩;n为桩基中的桩数。
2.2 水平力作用下基桩承载力计算
以桩身最大弯矩按受弯构件进行桩身受弯承载力计算,以桩身最大剪力按受剪构件进行桩身受剪承载力计算。桩的受弯承载力由混凝土和纵筋提供,抗剪承载力由混凝土和箍筋提供。同时,钢筋的配置应满足相关规范的构造要求[23-24]。
1)桩身受弯承载力计算式为
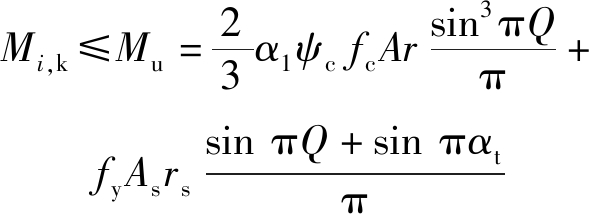
(21)
式中:Mu为桩身抗弯承载力设计值;α1为受弯构件矩形应力图应力取值为混凝土轴心抗压强度设计值时的折减系数;ψc为基桩成桩工艺系数,干作业灌注桩取0.9,泥浆护壁或套管护壁灌注桩取0.7~0.8;fc为混凝土轴心抗压强度设计值;A为桩身截面面积;r为桩身截面半径;fy为纵向主筋抗拉强度设计值;As为纵向主筋截面面积;rs为纵向主筋重心所在圆周的半径;Q为对应于受压区混凝土截面面积的圆心角与2π的比值,由公式
解之得,αt为纵向受拉钢筋截面面积与全部纵向钢筋截面面积的比值为αt=1.25-2Q,当Q>0.625时,取αt=0。
2)桩身受剪承载力计算式为
Hi,k≤Vu=1.971 2ψcftr2+1.6fyvAsvrcos β/s
(22)
式中:Vu为桩身受剪承载力设计值;ft为混凝土轴心抗拉强度设计值;fyv为箍筋抗拉强度设计值;Asv为同一截面内箍筋各肢的全部截面面积;s为箍筋间距;β为箍筋与正截面所成角度。
3 设计算例
钢筋混凝土桩筏基础如图3所示,桩径800 mm,桩长40 m,混凝土为C35,钢筋为HRB335。筏板平面尺寸D×B=17 m×11 m,最外排桩中心距y′轴线距离为7.5 m。筏板底部中心处作用总水平集中力为1 920 kN,总弯矩为2 400 kN·m,总竖向力为6 500 kN。桩的常规设计配筋为纵筋10Φ16,箍筋为螺旋箍筋Φ8。预计建筑所在场地内地表最大水平变形为2 mm/m。地基土水平抗力系数的比例系数m=10 MN/m4。计算在水平力作用下,并考虑采动地表水平变形作用后桩的配筋设计。
根据式(19)和式(20),可得各桩顶水平集中力为
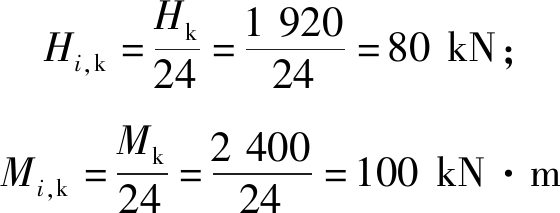
根据式(17)群桩最外侧桩顶处地基土体位移,得
Δlmax=0.85×1.2×2×7.5=15.3 mm
将Δlmax代入式(18),反算土体位移作用下桩顶的等效集中水平力H′0=25 kN;根据式(15)和式(16),得桩身最大弯矩210 kN·m,最大剪力105 kN;按式(21)和式(22),进行抗弯和抗剪承载力计算,根据计算结果,基桩至少需要配置纵筋为10Φ18,箍筋为Φ10。由此可见,在算例所给条件下,考虑地基土体水平变形后,纵筋直径由16 mm增加到18 mm,配筋量增加约26%;箍筋直径由8 mm增加到10 mm,配筋量增加约56%。
4 结 论
1)地基反力系数法为水平荷载作用下钢筋混凝土灌注桩(柔性长桩)内力计算时的常用方法。该方法假定桩侧土水平抗力与该点水平位移成正比,且地基系数随深度呈线性增长。
2)在水平力作用下,桩身最大弯矩位于桩顶下一定深度处,最大剪力位于桩顶处。在地基土体水平变形作用下,群桩最外侧的基桩处土体相对移动量最大,并以此最大移动量作为设计依据。
3)在桩基承台底部设置滑动层可以有效减少地基土体传递给承台及上部结构的摩擦力,减少了承台及上部结构的附加应力,从而间接提高了建筑物的整体抗变形能力。
4)在计算算例所给已知条件下,考虑地基土体水平变形影响下的基桩抗弯和抗剪承载力计算配筋结果表明,考虑地基土体水平变形作用后,桩基的纵筋和箍筋配筋量较常规水平力作用下的配筋量分别增加了约26%和56%。
参考文献(References):
[1] 滕永海,唐志新.老采空区地面建筑技术研究及应用[J].煤炭科学技术,2016,44(1):183-186.
TENG Yonghai,TANG Zhixin.Research and application of ground construction technology in old goaf [J].Coal Science and Technology,2016,44(1):183-186.
[2] 李树志.采煤沉陷区城市建设关键技术研究与应用[J].煤矿开采,2016,21(2):73-77.
LI Shuzhi.Research and application of key technologies for urban construction in mining subsidence area [J].Coal Mining,2016,21(2):73-77.
[3] 滕永海,张俊英.老采空区地基稳定性评价[J].煤炭学报,1997,22(5):58-62.
TENG Yonghai,ZHANG Junying.Foundation stability evaluation of old goaf [J].Journal of China Coal Society,1997,22(5):58-62.
[4] 滕永海.采动过程中地表移动变形计算研究[J].矿山测量,1997(4):17-20,50.
TENG Yonghai.Studyon calculation of surface movement and deformation in mining process [J].Mine Surveying,1997(4):17-20,50.
[5] 滕永海,唐志新,易四海.采煤塌陷区高层建筑地基评价与抗变形技术[J].矿山测量,2016(1):1-6.
TENG Yonghai,TANG Zhixin,YI Sihai.Foundation evaluation and anti deformation technology of high-rise buildings in mining subsidence area [J].Mine Surveying,2016(1):1-6.
[6] 徐 起,朱 伟,滕永海,等.采煤塌陷区上方大型厂房建设技术研究[J].金属矿山,2019(10):153-157.
XU Qi,ZHU Wei,TENG Yonghai,et al.Study on construction technology of large workshop above mining subsidence area [J].Metal Mine,2019(10):153-157.
[7] 张俊英.抗变形砖混、框架结构受力体系研究[J].东北煤炭技术,1996(4):11-14.
ZHANG Junying.Study on the stress system of brick concrete and frame structure with anti deformation [J].Northeast Coal Technology,1996(4):11-14.
[8] 张俊英.滑动层对抗变形框架结构建筑物的作用分析[J].矿山测量,1994(3):29-32.
ZHANG Junying.Analysis of the effect of sliding layer on deformation frame structure buildings [J].Mine Surveying,1994(3):29-32.
[9] 唐志新,黄乐亭,张俊英,等.采动区煤矸石地基分层振动碾压试验[J].土工基础,1997,11(1):17-20.
TANG Zhixin,HUANG leting,ZHANG Junying,et al.Layered vibration rolling test of coal gangue foundation in mining area [J].Soil Engineering and Foundation,1997 ,11(1):17-20.
[10] 夏军武,袁迎曙,董正筑.采动区地基、条形基础与框架结构共同作用机理研究[J].岩土工程学报,2007,29(4):537-541.
XIA Junwu,YUAN Yingshu,DONG Zhengzhu.Study on interaction mechanism of foundation,strip foundation and frame structure in mining area [J].Chinese Journal of Geotechnical Engineering,2007,29(4):537-541.
[11] 夏军武,袁迎曙,董正筑.采动区地基、独立基础与框架结构共同作用的力学模型[J].中国矿业大学学报,2007,30(1):33-37.
XIA Junwu,YUAN Yingshu,DONG Zhengzhu.Mechanical model of interaction of foundation,independent foundation and frame structure in mining area [J].Journal of China University of Mining and Technology,2007,30(1):33-37.
[12] 陈希哲,叶 菁.土力学地基基础[M].北京:清华大学出版社,2013.
[13] 薛玉洁.复合桩基在采空区建构筑物基础中的应用研究[D].徐州:中国矿业大学,2016.
[14] 盛 平,于广云,李小琴.采动区表土水平移动对桩基作用的数值模拟研究[J].煤炭科学技术,2006,34(10):66-69.
SHENG Ping,YU Guangyun,LI Xiaoqin.Numerical simulation of the effect of horizontal movement of topsoil on pile foundation in mining area [J].Coal Science and Technology,2006,34(10):66-69.
[15] 杨建平,朴春德,常鸿飞,等.水平荷载下灌注桩变形分布式检测及承载机制研究[J].岩石力学与工程学报,2014,33(S1):2983-2988.
YANG Jianping,PIAO Chunde,CHANG Hongfei,et al.Study on distributed detection and bearing mechanism of cast-in-place pile deformation under horizontal load [J].Chinese Journal of Rock Mechanics and Engineering,2014,33 (S1):2983-2988.
[16] 常林越,王金昌,朱向荣.水平联合荷载作用下长桩弹塑性解析计算研究[J].岩土工程学报,2010,32(6):916-923.
CHANG Linyue,WANG Jinchang,ZHU Xiangrong.Study on elastic-plastic analysis of long pile under horizontal combined load [J].Chinese Journal of Geotechnical Engineering,2010,32(6):916-923.
[17] 苏 栋,李相崧.水平多向荷载下桩-土相互作用初探[J].岩土力学,2008,29(3):603-608.
SU Dong,LI Xiangsong.Preliminary study on pile-soil interaction under horizontal multi-directional load [J].Rock and Soil Mechanics,2008,29(3):603-608.
[18] 雷建伟,王 盛.按m法计算弹性桩水平位移及作用效应[J].工程建设与设计,2019(24):32-33.
LEI Jianwei,WANG Sheng.Calculation of horizontal displacement and action effect of elastic pile by m method [J].Engineering Construction and Design,2019(24):32-33.
[19] 劳伟康,周治国,周立运.水平推力桩在大位移情况下m值的确定[J].岩土力学,2008,29(1):192-196.
LAO Weikang,ZHOU Zhiguo,ZHOU Liyun.Determination ofm value of horizontal thrust pile under large displacement [J].Rock and Soil Mechanics,2008,29(1):192-196.
[20] 龚晓南.桩基工程手册[K].2版.北京:中国建筑工业出版社,2016:225-309.
[21] 何国清,杨 伦,凌赓娣,等.矿山开采沉陷学[M].徐州:中国矿业大学出版社,1991.
[22] [苏]尤申(А·И·юшин) .采动区建筑物基础设计要点[M] .郭福君,刘树滋 译.北京:煤炭工业出版社,1986.
[23] GB 50010—2010,混凝土结构设计规范[S].
[24] JGJ 94—2008,建筑桩基技术规范[S].
