0 引 言
济宁市城市周边存在多个煤矿的开采,近年来,随着城市建设的快速发展,由2016年所发布的《济宁市城市总体规划(2014—2030年)》[1]中划定的济宁市中心城区规划范围与多个煤矿矿区范围重叠,且这些矿井大部分为生产矿井,因此,确定济宁城市规划区的开采沉陷规律,对指导区域内各矿井后续开采活动与城市建设的协调统一具有重要作用。
自各区域矿井建矿以来,积累了丰富的地表移动变形观测实测资料,各研究者对部分资料进行了整理分析,得出了一些有用的结论。李运江等[2]通过分析鲍店井田西部第四系地层富水性、颜色、岩性、电性特征及厚度等因素进行了第四系上中下组划分,分析了含水层的富水性和隔水层的隔水性对进一步提高开采上限的影响;邵小朋等[3]根据许厂矿物探、钻探和生产过程中的资料,采用地质统计法对断裂构造要素进行统计分析,建立了断层落差与延展长度之间的经验公式,定量分析了断层落差与延展长度之间的关系;吴新庆等[4]通过对钻井数据的统计、沉积相和构造特征的综合分析,研究了许厂煤矿井田内3下煤层的厚度变化特点及其成因;邵小朋等[5]系统的研究分析了许厂煤矿地质构造发育特征,对矿区不同期次构造应力场特征和构造机理进行了探讨;李小明等[6]采用模糊综合评判法对许厂煤矿3下煤层构造进行了分析评价,对矿井高效生产提供了一定指导依据;许东等[7]对济宁矿区1984-2013年的塌陷积水面积进行测算,分析了近30年来济宁采煤塌陷积水区的扩展变化情况;卞景强等[8]分析了东滩煤矿围岩压力监测数据,研究开采时迎头压力变化规律、岩石断裂时的声发射活动特征;李世民[9]以山东田庄煤矿1301工作面为例,采用滑移线场理论和FLAC3D数值模拟方法得出的煤层底板采动破坏深度,并根据垂直应力分布云图解释了煤层底板发生破坏的原因;夏文营[10]对田庄煤矿勘探成果资料和生产资料的对比研究,总结出矿区的煤质变化规律,为合理开发利用资源并优化资源配置提供了依据;葛春等[11]以瓦斯地质理论、煤田地质学为基础,结合岱庄煤矿地质特征以及瓦斯基础测试参数,对该矿煤层瓦斯地质规律进行了分析;赵元强等[12]分析了矿区水文地质条件,根据对矿区不同煤层突水系数的分析计算,分析了不同煤层采动的安全性;王宗胜等[13]综合分析了鲍店煤矿开采沉陷预计参数;谭志祥等[14]探讨了高强度综放开采条件下的地表沉陷变形规律,得到鲍店矿区域沉陷仍符合概率积分法的结论;贺天[15]等分析了济宁三号煤矿重复采动条件下的矿区地表沉陷规律,解算了地表移动变形参数,分析了地表移动情况及影响因素;王永辉等[16]分析得横河煤矿巨厚松散层下煤炭开采引起的地表沉陷变形分布符合概率积分法模型,并据此开展了移动变形分析工作;常西坤[17]以唐口煤矿以研究对象,分析了深部开采覆岩形变及地表移动特征的实验研究;郭振忠等[18]以许厂煤矿为例,用数学方法分析了厚松散层下地表沉陷的特征及岩移参数;陈铃[19]通过获取济宁市煤矿集区最新的GeoEye-1高空间分辨率遥感影像并结合历史资料分析研究区域内地面沉陷产生的灾害情况,为评估各煤矿区的灾害影响提供了大量资料,为分析比较各矿沉降的原因差异提供了真实的数据;刘传富[20]利用双轨D-InSAR技术获取济宁矿区的地面沉降分布以及各沉降区在监测时间段内的沉降量及沉降面积等信息,为治理煤矿区引起的地面沉降情况提供了一定的技术支持与借鉴。
除上述成果外,国内外学者针对济宁城市规划区内各矿井的开采沉陷工作还开展了许多卓有成效的研究工作,成功地指导了煤矿的开采及地表塌陷的治理工作。但是,已有成果的研究范围大部分为仅针对单个煤矿单个工作面开展的,而涉及整个区域的研究成果较少,因此,以济宁城市规划区为研究范围,整理分析区域内各矿井有效实测资料,以期望得到能在范围内推广应用的开采沉陷规律。
1 区域概况
新规划划定的济宁城市规划区范围包括任城区、兖州区,邹城市、曲阜市、嘉祥县等街道和部分乡镇,主要涉及了济宁煤田、兖州煤田和宁阳-汶上煤田三大煤田的23个煤矿,各矿区与城市规划区的分布关系如图1所示。区域中,兴隆庄煤矿为最早投产煤矿,投产时间为1981年。济宁煤田安居煤矿为最晚投产煤矿,投产时间为2015年。按照生产规模划分,除了何岗和太平煤矿为小型煤矿之外,其余煤矿均为中大型煤矿。截至2018年12月,研究区内现有煤矿采空工作面1 982个,采空区埋深170~1 200 m不等,开采煤层厚度0.8 ~10.2 m不等。研究区各矿山以开采3煤、3上煤、3下煤为主,其他还包括2煤、15上煤、16煤、16上煤、17煤;除葛亭煤矿暂无开采规划,其余各矿井均有长、短期开采规划。
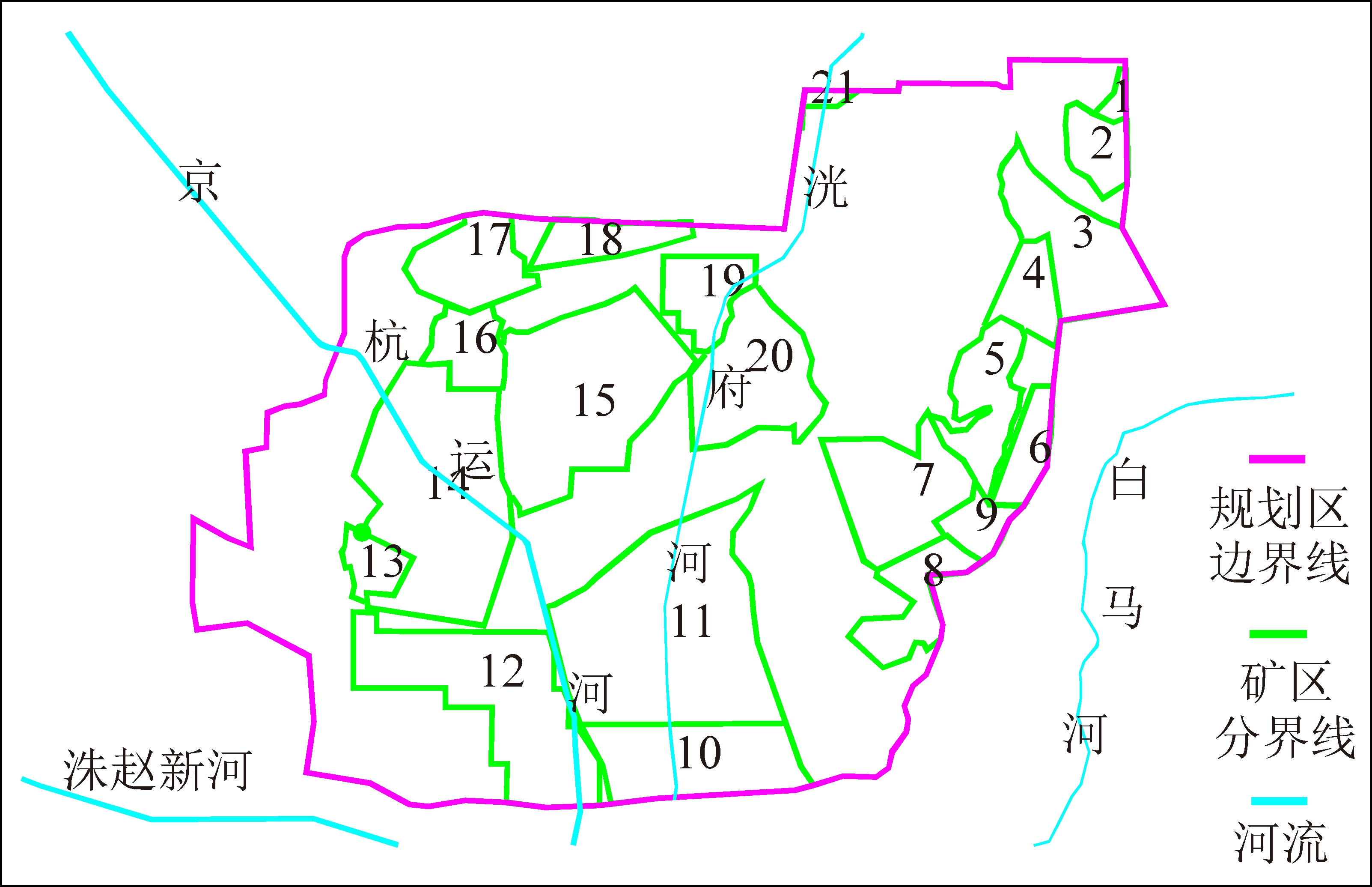
1—21依次为:单家村煤矿、古城煤矿、兴隆庄煤矿、大统一煤矿、 杨村煤矿、鲍店煤矿、田庄煤矿、太平煤矿、横河煤矿、济三煤矿、 济二煤矿、安居煤矿、新河煤矿、唐口煤矿、岱庄煤矿、运河煤矿、 葛亭煤矿、鲁西煤矿、何岗煤矿、许厂煤矿、新驿煤矿
图1 城市规划区与各矿区分布关系
Fig.1 Distribution relationship between urban planning area and mining areas
2 各矿观测资料情况
济宁市规划区域中许多煤矿在不同矿井的生产阶段中均开展了地表开采沉陷观测工作,通过多方资料的收集整理,获取了岱庄煤矿各观测站的综合分析结果和其余13个矿井的20个观测站数据处理结果。其中,各观测站工作面基本情况见表1。
表1 各观测站工作面基本信息
Table 1 Basic information on working
face of observation stations
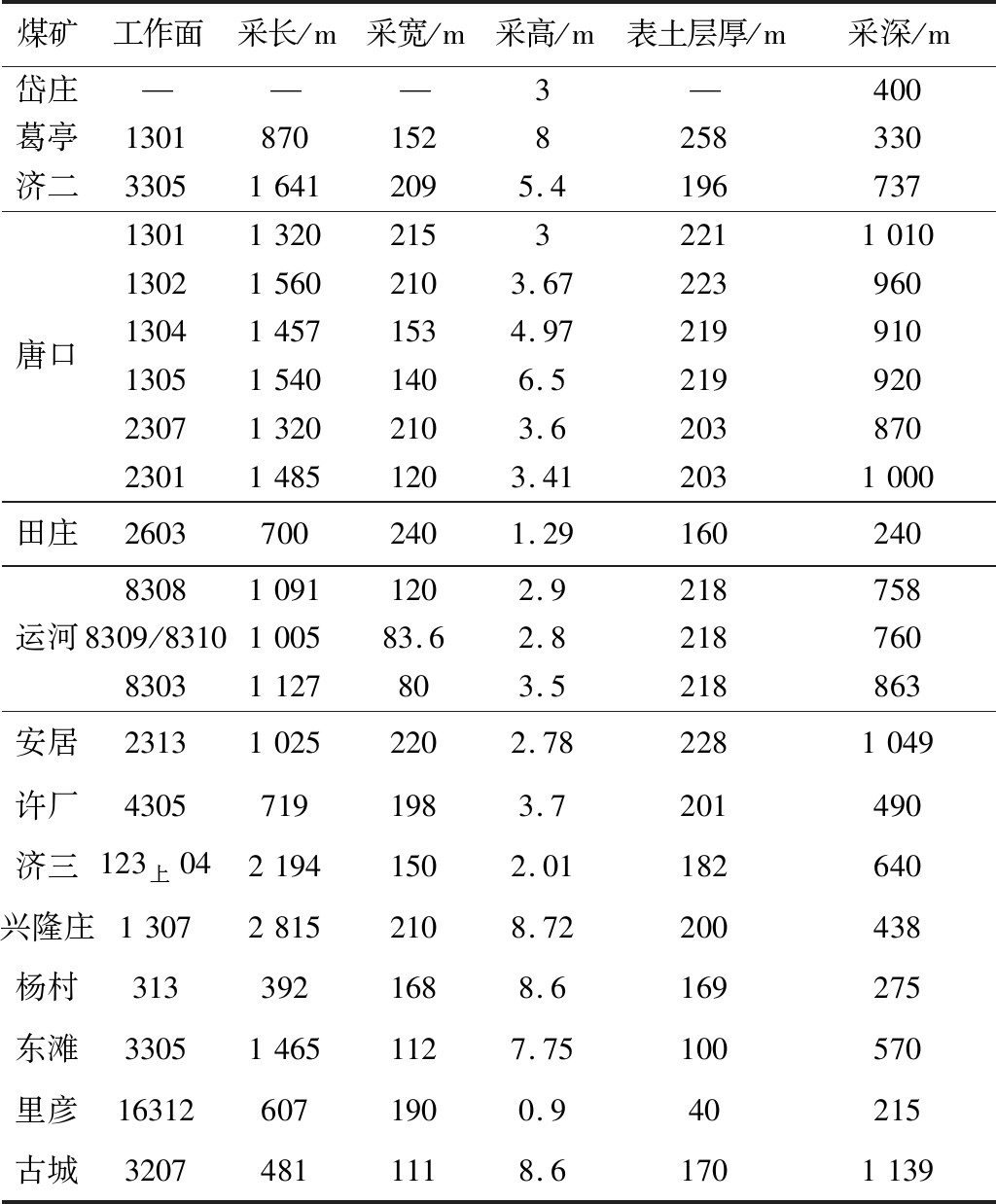
煤矿工作面采长/m采宽/m采高/m表土层厚/m采深/m岱庄———3—400葛亭13018701528258330济二330516412095.4196737唐口1301132021532211010130215602103.67223960130414571534.97219910130515401406.5219920230713202103.6203870230114851203.412031000田庄26037002401.29160240运河830810911202.92187588309/8310100583.62.821876083031127803.5218863安居231310252202.782281049许厂43057191983.7201490济三123上0421941502.01182640兴隆庄130728152108.72200438杨村3133921688.6169275东滩330514651127.75100570里彦163126071900.940215古城32074811118.61701139
求取的概率积分法参数见表2,表中空缺项为由于监测数据的缺失无法获取有效结果。
表2 各观测站工作面概率积分法参数
Table 2 Parameters of probability integral method for working faces of observation stations
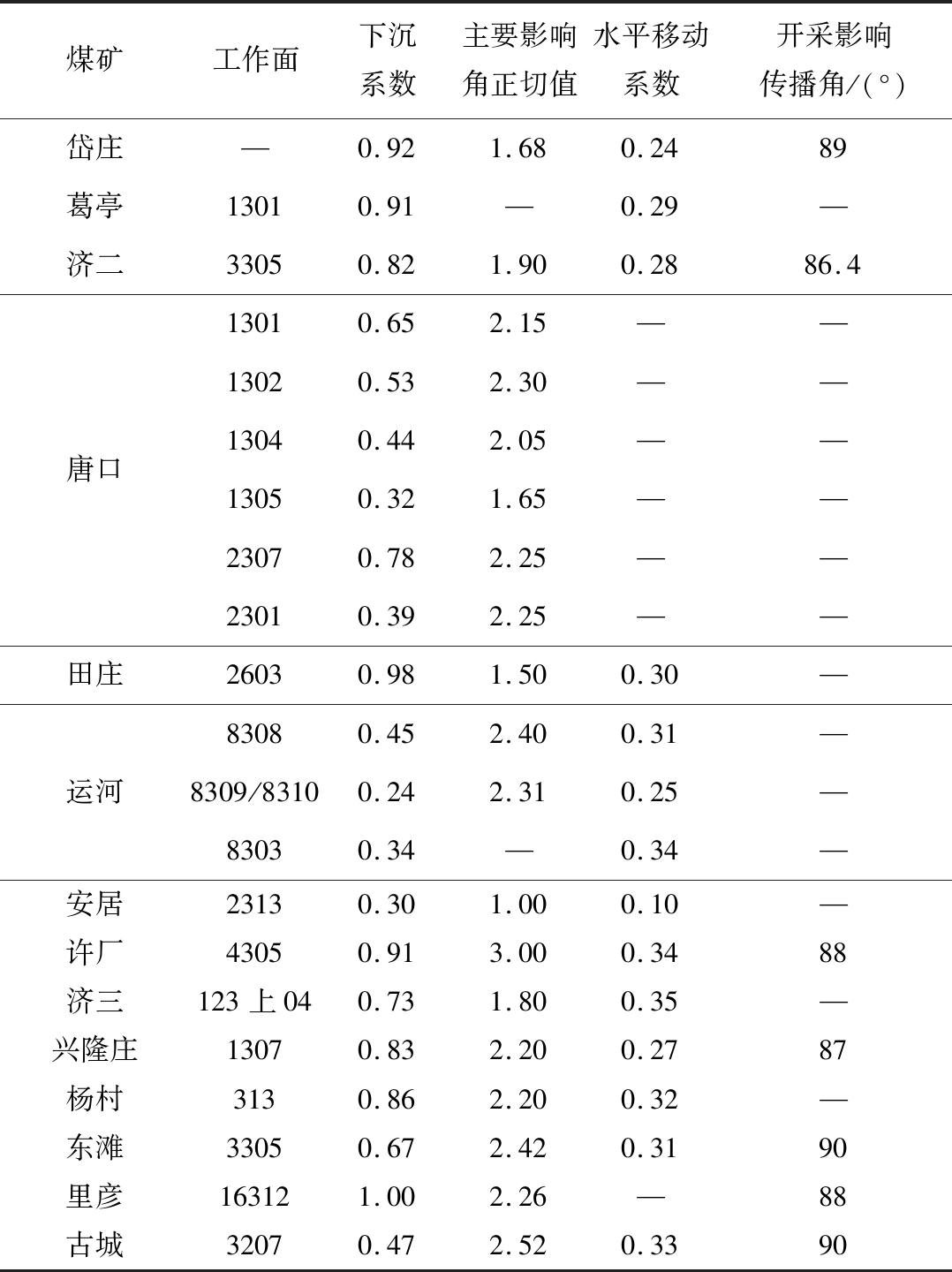
煤矿工作面下沉系数主要影响角正切值水平移动系数开采影响传播角/(°)岱庄—0.921.680.2489葛亭13010.91—0.29—济二33050.821.900.2886.4唐口13010.652.15——13020.532.30——13040.442.05——13050.321.65——23070.782.25——23010.392.25——田庄26030.981.500.30—运河83080.452.400.31—8309/83100.242.310.25—83030.34—0.34—安居23130.301.000.10—许厂43050.913.000.3488济三123上040.731.800.35—兴隆庄13070.832.200.2787杨村3130.862.200.32—东滩33050.672.420.3190里彦163121.002.26—88古城32070.472.520.3390
3 概率积分法参数综合分析
在上述观测资料的基础上,综合分析济宁城市规划区范围内开采沉陷概率积分法参数与表土层厚度、采深、采高、充分采动程度等因素的关系,以获得可在全区范围内推广应用的规律。
3.1 下沉系数
3.1.1 单变量分析
下沉系数与各因素之间的关系如图2所示。
1)表土层厚度:从图2a可知,在表土层厚度为160~228 m时,下沉系数与表土层系数具有良好的强线性关系,即下沉系数随表土层厚度的增加呈现线性减小趋势。其拟合函数为
y=-0.010 52 x+2.634 61,R2=0.591 69
2)开采深度:由图2b可知,下沉系数与开采深度在整体上存在着明显的强线性相关性,随着开采深度的加深,下沉系数对应减小。当开采深度为215~1 139 m时,其拟合函数关系式为
y=-7.3 942 6×10-4x+1.145 57,R2=0.858 05
3)开采高度:从图2c中可知,下沉系数与采高在局部范围内存在二次函数关系,当采高处于0.95~6.45 m时,其拟合函数关系式为

图2 下沉系数随各因素关系
Fig.2 Relationship between subsidence coefficient and each of factors
y=0.016 84x2-0.245 79x+1.217 89,
R2=0.980 33
4)采动程度:由图2d可知,整体上表现出随采动程度的逐渐增大,下沉系数为非线性增加。即:当采动程度处于0.33~0.99时,其拟合函数关系式为y=0.431 74x4+1.841 95x3-5.182 3x2+3.941 72x-0.027 76,R2=0.814 32
3.1.2 多变量综合分析
利用主成分回归法分析表土层厚度、开采高度和开采深度等因素对下沉系数的综合影响。具体选取数据见表3。
表3 参数选取数据
Table 3 Selected data of parameters
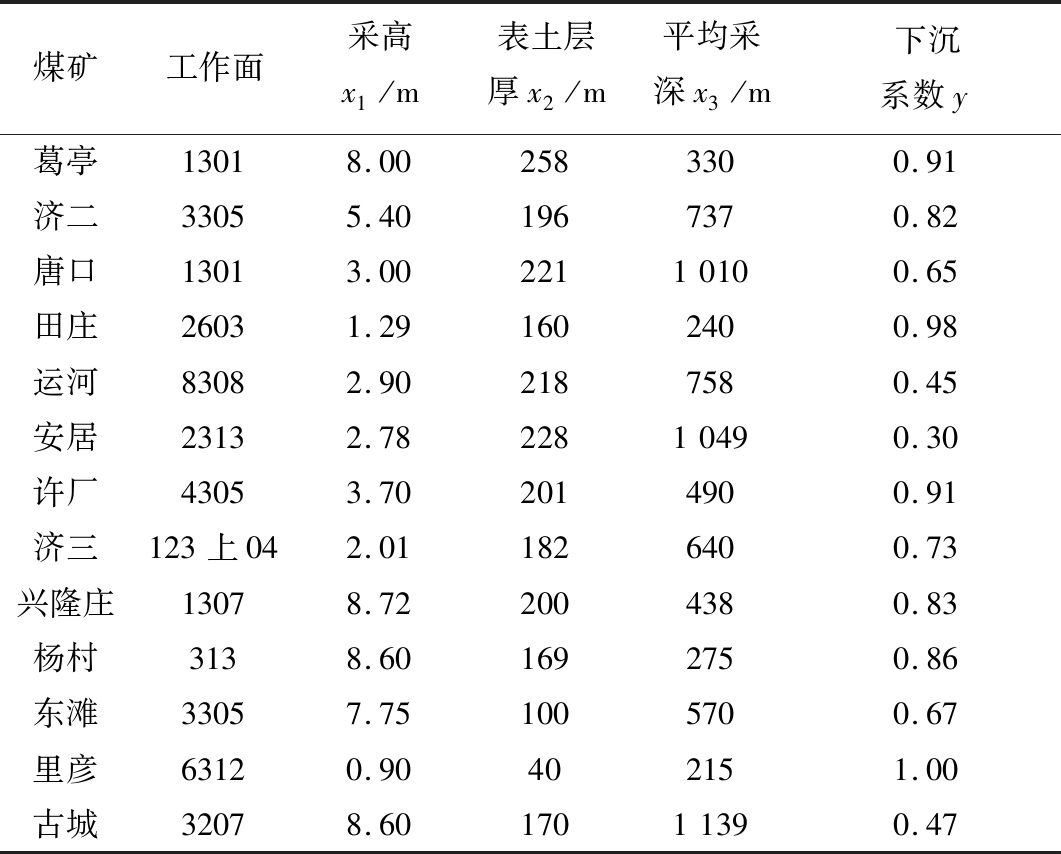
煤矿工作面采高x1/m表土层厚x2/m平均采深x3/m下沉系数y葛亭13018.002583300.91济二33055.401967370.82唐口13013.0022110100.65田庄26031.291602400.98运河83082.902187580.45安居23132.7822810490.30许厂43053.702014900.91济三123上042.011826400.73兴隆庄13078.722004380.83杨村3138.601692750.86东滩33057.751005700.67里彦63120.90402151.00古城32078.6017011390.47
主成分回归分析[21]是将大量相关性很高的变量转化为彼此互相独立或不相关的变量,通过选取主要影响变量作为主成分来进行综合性分析的降维性回归分析方法。
3.1.3 数学模型
设有n个样本,每个样本有p个变量因子:x1,x2,x3,…,xp,得到其原始数据矩阵Xn×p:
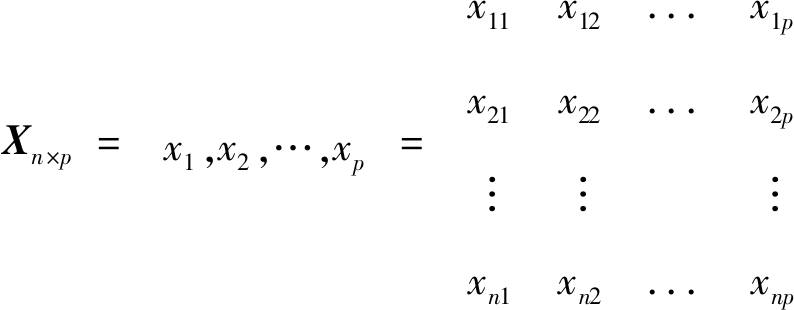
(1)
1)原始矩阵Xn×p标准化变换后得到归一化矩阵Zn×p:
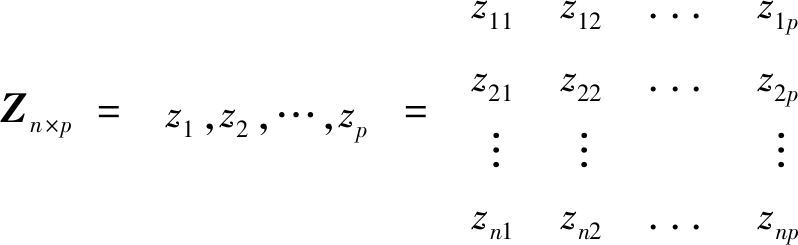
(2)
其中,标准归化阵Zn×p的相关矩阵![]()
2)求解R特征值λi以及对应的特征向量bi为
Rbi=λibi
(3)
3)求取变量主成分向量Ui为
第i主成分ui满足:
(4)
根据特征值贡献度wi选择样本主成分以及对应的特征向量bi,即有
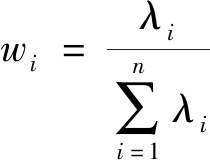
(5)
Ui=Zbi (i=1,2,…,n)
(6)
4)建立主成分因子回归函数模型
对选定j个主成分的特征向量Ui进行单位正交化得向量Ci:Ci=(cx1,cx2,…,cxp),其中Ci满足条件:
(7)
(8)
其中,wi为特征值贡献率;β为方程常数项。式(8)为主成分线性回归方程,计算结果见表4。
表4 归一化变量主成分特征
Table 4 Principal component characteristics of normalized variables
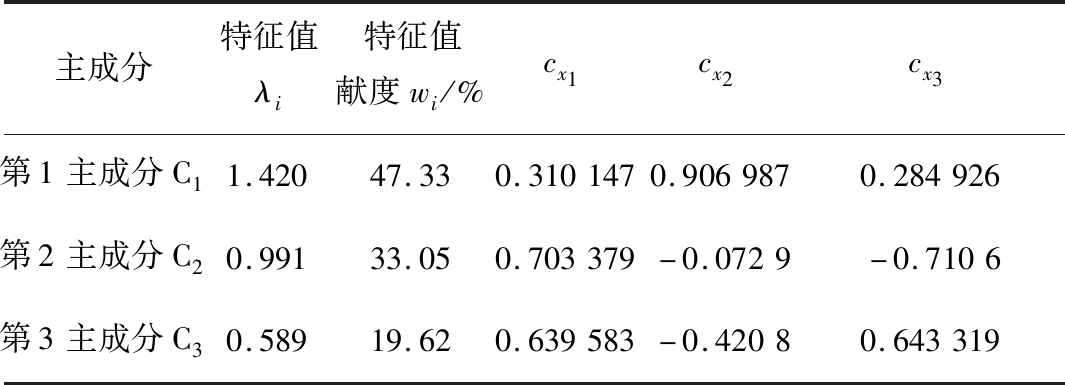
主成分特征值λi特征值献度wi/%cx1cx2cx3第1主成分C11.42047.330.3101470.9069870.284926第2主成分C20.99133.050.703379-0.0729-0.7106第3主成分C30.58919.620.639583-0.42080.643319
表中λ1为标准化相关矩阵的特征值,wi为公式(5)计算得到的特征值贡献度,cx1,cx2 ,cx3分别为各主成分特征向量Ui单位正交化后的向量。
主成分回归计算得其函数模型方程为
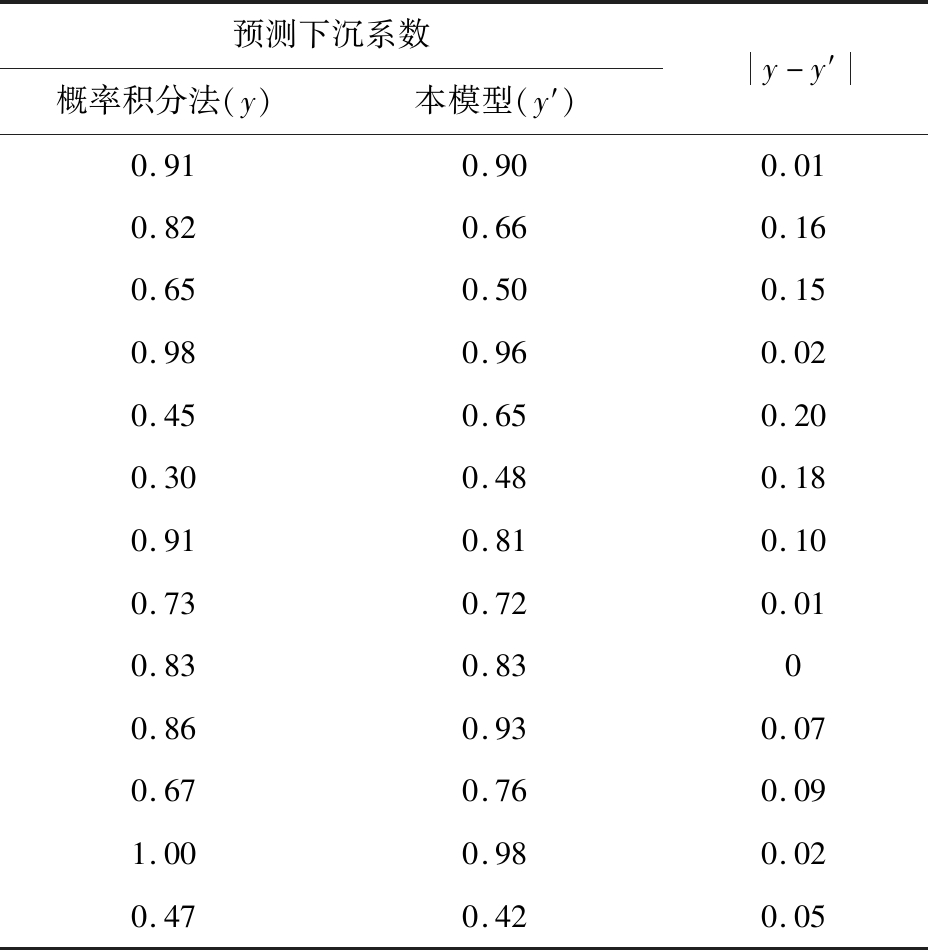
y=-1.4×10-4x1-2.248 5×10-5x2-5.960 2×10-4x3+1.109 7。该回归模型预测与概率积分法预测对比见表5 。
由表5可知:二者之间的最大差值max{|y-y′|}=0.18,中误差σ=0.127 5。所建模型方程与概率积分法模型预测值基本保持一致,该模型将少量影响因子组合一定程度上简化了复杂的概率积分法预测模型。在实际工程项目数据不全的情况下提供了重要的参考价值。并由该综合函数模型分析得各因子对下沉系数的影响依次为:表土层厚度>开采深度>开采高度。与单因子分析所得趋势结论保持一致。
表5 主成分回归法与概率积分法预测结果对比
Table 5 Comparison of prediction results between principal component regression analysis and probability integral method
预测下沉系数概率积分法(y)本模型(y′)y-y′0.910.900.010.820.660.160.650.500.150.980.960.020.450.650.200.300.480.180.910.810.100.730.720.010.830.8300.860.930.070.670.760.091.000.980.020.470.420.05
3.2 水平移动系数
水平移动系数与各因素之间的关系绘制图如图3所示。
1)表土层厚度:水平移动系数主要集中分布在0.25~0.35中。由图3a可知,经统计拟合可知:二者在局部上存在二次函数的关系。即当表土层厚度处于168~228 m时,二者的拟合函数关系式为:y=-5.382 49×10-5x2+0.020 5x-1.002 46,相关系数为R2=0.938 66。
2)开采高度:水平移动系数主要集中分布在0.25~0.35,由图3b可知,在统计范围内,水平移动系数的期望值约为0.31。且整体上呈现出随着开采高度的增加,水平移动系数呈现减小趋势。
3)开采深度:水平移动系数与开采深度无明显统计规律。从图3c可知,当开采深度处于240~863 m时,水平移动系数在0.27~0.35波动。
4)采动程度:水平移动系数与采动程度无明显统计规律。由图3d可知,当采动程度处于0.09~0.61时,水平移动系数基本分布在0.27~0.35。
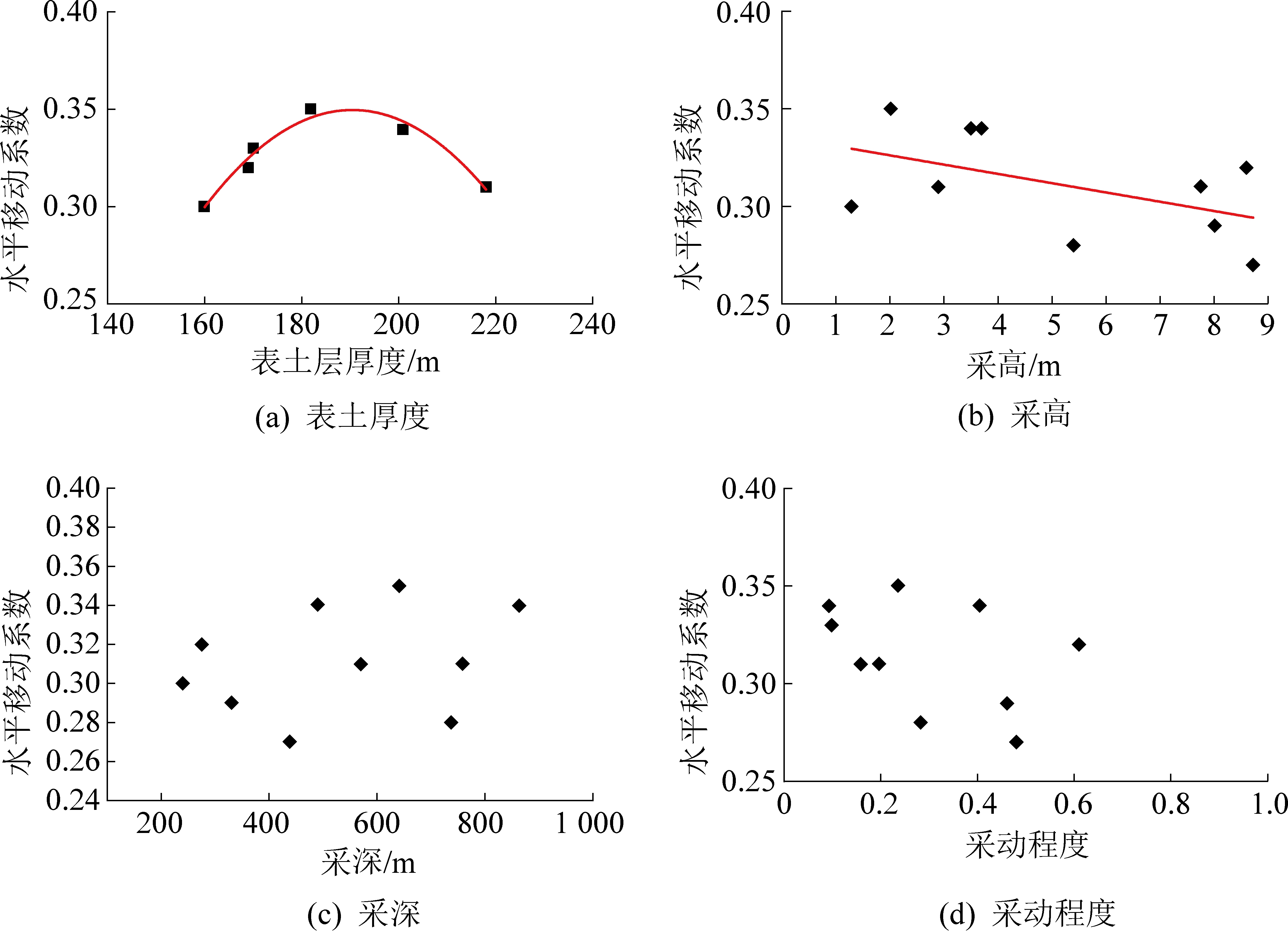
图3 水平移动系数随各因素关系
Fig.3 Relationships between coefficient of horizontal movement and each of factors
3.3 主要影响角正切
主要影响角正切与各因素之间的关系如图4所示。
1)表土层厚度:由图4a可知,主要影响角正切与表土层厚度在局部上呈现出线性相关性。即表土层厚度集中处于160~223 m时,与主要影响角正切
值拟合函数关系式为
y=7.93×10-5x+0.499 91,R2=0.450 73
2)开采高度:从图4b中可知,经过统计拟合后,主要影响角正切与开采高度存在呈现出“波浪”变化形态。即开采高度处于1.42~8.60 m时,拟合函数关系式为
y=-0.003 52x5+0.077 44x4-0.656 97x3+2.356 06x2-3.197 1x+2.917,R2=0.857 9
3)开采深度:由图4c可知,主要影响角随开采深度呈现出线性增长趋势。当开采深度为215~1 139 m时,其拟合函数表达式为
y=4.198 67×10-4x+1.834 83,R2=0.208 44
4)采动程度:由图4d可知,主要影响角与采动程度无明显统计变化规律,经统计得:主要影响角正切值为1.6~2.5。
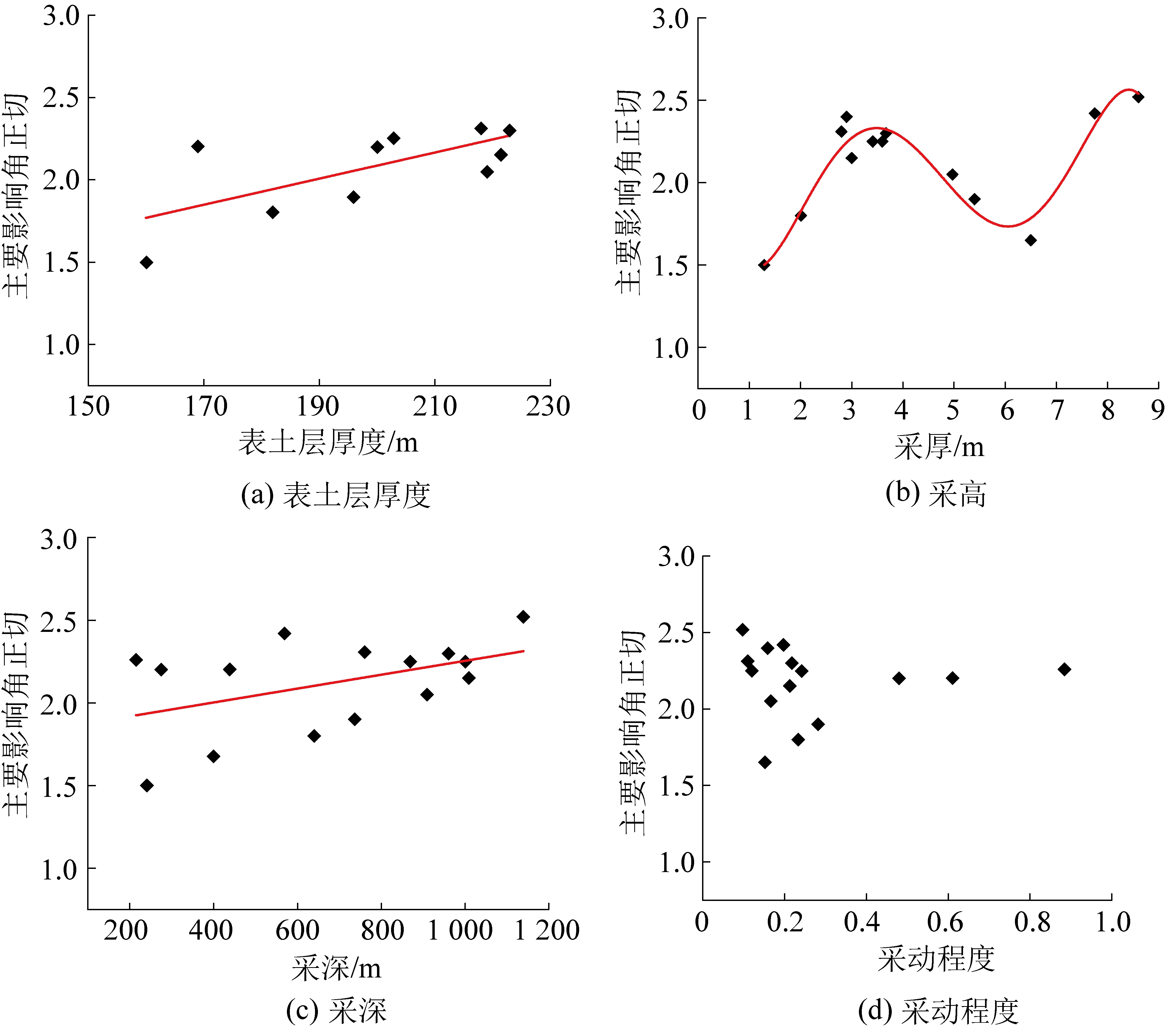
图4 主要影响角正切随各因素关系
Fig.4 Relationships between tangent of main influence angle and each of factors
4 结 论
综合收集整理了济宁城市规划区13个矿井的20条观测站资料,并对所求取的概率积分法参数进行综合分析,获得4条结论。
1)评价区域内下沉系数受到了采动程度和开采深度的明显制约。下沉系数随采动程度增大呈现增大趋势,而随开采深度的增大呈现出减小的趋势。各因子对下沉系数的影响程度上表现为:表土层厚度>开采高度>开采深度。
2)水平移动系数与开采深度、开采高度、表土层厚度和采动程度间没有明显统计相关性。经统计拟合后,水平移动系数与表土层厚度在局部上具有二次函数相关性,且随采高的增加呈现出减小的趋势。
3)主要影响角正切与表土层厚度在局部存在线性相关性。而与开采深度具有一定的线性关系,即开采深度不断增加,主要影响角正切呈现增大趋势。开采高度与主要影响角正切之间存在“波浪”函数关系,但与采动程度无明显相关性。
4)开采影响传播角在本研究区域内比较稳定,处于86.4°~90.0°。
参考文献(References):
[1] 山东省人民政府关于《济宁市城市总体规划(2014-2030年)》的批复:http://www.shandong.gov.cn/art/2017/1/6/art_2259_24212.html.
[2] 李运江,王宗胜,鲁 亮.鲍店井田西部第四系划分及对提高开采上限的影响[J].山东煤炭科技,2014(4):159-161.
LI Yunjiang,WANG Zhongsheng,LU Liang.The Quaternary stratigraphic division in western Baodian mining field and to improve the influenc [J].Shandong Coal Science and Technology,2014(4):159-161.
[3] 邵小朋,徐旭东,南莹浩.许厂煤矿断裂构造规律研究[J].华北科技学院学报,2017,14(4):19-23,51.
SAHO Xiaopeng,XU Xudong,NAN Yinghao.Study on fault structure of Xuchang coal mine [J].Journal of North China Institute of Science and Technology,2017,14(4):19-23,51
[4] 吴新庆,袁黎明,曹 健.浅析许厂煤矿3下煤层厚度变化规律及其影响因素[J].山东煤炭科技,2015(4):26-27.
WU Xinqing,YUAN Liming,CAO Jian.Research on change law and influential of the No.3 lower coal seam thickness in Xuchang mine field[J].Shandong Coal Science and Technology,2015(4):26-28.
[5] 邵小朋,徐旭东,南莹浩.许厂煤矿地质构造特征及其演化[J].华北科技学院报,2017,14(6):25-2.
SHAO Xiaopeng,XU Xudong,NAN Yinghao.Geological structure and evolution of Xuchang coal mine[J].Journal of North China Institute of Science and Technology,2017,14(6):25-27.
[6] 李小明,邵小朋,连会青.基于模糊综合评判法的地质构造复杂程度评价:以许厂煤矿330采区为例[J].中国煤炭地质,2019,31(3):6-11.
LI Xiaoming,SHAO Xiaopeng,LIAN Huiqing.Geological structural complexity assessment based on fuzzy comprehensive assessment method:a case study of No.330 winning district Xuchang coal mine [J].Coal Geology of China,2019,31(3):6-11.
[7] 许 冬,吴 侃.济宁煤矿区地表塌陷积水时空演变[J].辽宁工程技术大学学报(自然科学版),2014,33(10):1307-1311.
XU Dong,WU Kan.Spatial-temporal evolution of collapse waterlogged region in Jjining coal mining area[J].Journal of Liaoning Technical University(Natural Science),2014,33(10):1307 -1311.
[8] 卞景强,闫宪洋,谭文峰,等.东滩煤矿初掘巷道围岩压力监测分析[J].煤矿现代化,2014,122(5):80-82.
BIAN Jingqiang,YAN Xianyang,TAN Wenfeng,et al.Monitoring and analysis on surrounding rock pressure of initial excavation tunnel in Dongtan coal mine[J].Coal Mine Modernization,2014,122(5):80-82.
[9] 李世民.山东田庄煤矿深部薄煤层开采底板破坏特征[J].现代矿业,2018,34(3):135-137.
LI Shimin.Floor failure characteristics of the thin coal seam in the depth of Tianzhuang coal mine in Shandong[J].Modern Mining,2018,34(3):135-137.
[10] 夏文营.田庄煤矿煤质变化规律分析[J].山东煤炭科技,2017(8):135-137.
XIA Wenying.Analysis of coal quality variation order liness in Tianzhuang coal mine[J].Shandong Coal Science and Technology,2017(8):135-137.
[11] 葛 春,李海锋,李传磊.淄矿岱庄煤矿瓦斯地质规律分析[J].中国高新技术企业,2014(10):89-91.
GE Chun,LI Haifeng,LI Chuanlei.Analysis on gas geology law of Daizhuang coal mine in zi mine[J].China High Technology Enterprises,2014(10):89-91.
[12] 赵元强,王同华,傅 静.葛亭煤矿1160采区水文地质条件分析[J].中国煤炭地质,2008,20(5):42-46.
ZHAO Yuanqiang,WANG Tonghua,FU Jing.Geting coal mine No.1160 winning district hydrogeological condition analysis[J].Coal Geology of China,2008,20(5):42-46.
[13] 王宗胜,谭志祥,李运江,等.鲍店矿区开采沉陷预计参数综合研究[J].矿山测量,2014(3):24-26.
WANG Zhongsheng,TAN Zhixiang,LI Yunjiang,et al.Comprehensive study on prediction parameters of mining subsidence in Baodian mining area[J].Mine Surveying,2014(3):24-26.
[14] 谭志祥,王宗胜,李运江,等.高强度综放开采地表沉陷规律实测研究[J].采矿与安全工程学报,2008,25(1):63-66.
TAN Zhixiang,WANG Zhongsheng,LI Yunjiang,et al.Field research on ground subsidence rules of intensive fully-mechanized mining by sublevel caving[J].Journal of Mining and Safety Engineering,2008,25(1):63-66.
[15] 贺 天,张自发,张广学.济宁三号煤矿重复采动条件下的矿区地表沉陷规律研究[J].山东煤炭科技,2019(6):144-146,149.
HE Tian,ZHANG Zifa,ZHANG Guangxue.Research on surface subsidence law of mining area under repeated mining condition in Jining No.3 coal mine [J].Shandong Coal Science and Technology,2019(6):144-146,149.
[16] 王永辉,倪岳晖,周建伟,等.基于概率积分法的横河煤矿巨厚松散层下开采沉陷预测分析[J].地质科技情报,2014,33(4):219-224.
WANG Yonghui,NI Yuehui,ZHOU Jianwei,et al.Subsidence prediction under thick and loose overburden of Henghe coal mine based on probability integration method[J].Geological Science and Technology Information,2014,33(4):219-224.
[17] 常西坤.深部开采覆岩形变及地表移动特征基础实验研究[D].青岛:山东科技大学,2010.
[18] 郭振忠,周业亭,孙少磊.基于许厂煤矿厚松散层下开采地表沉陷规律研究与应用[J].中国高新技术企业,2012(22):128-129.
GUO Zhenzhong,ZHOU Yeting,SUN Shaolei.Research and application of surface subsidence law based on mining under thick loose strata in Xuchang coal mine[J].China High Technology Enterprises,2012(22):128-129.
[19] 王海庆,陈 玲.山东省济宁市煤矿矿集区地面沉陷现状遥感调查[J].中国地质灾害与防治学报,2011,22(1):87-93.
WANG Haiqing,CHEN Ling.Investigation of current surface subsidence situation using remote sensing images in Jining coal mine[J].The Chinese Journal of Geological Hazard and Control,2011,22(1):87-93.
[20] 刘传富.D-InSAR在济宁矿区地面沉降监测中的运用[J].北京测绘,2018,32(2):239-244.
LIU Chuanfu.Application of differential D- InSAR in monitoring Jining mining-induced subsidence[J].Beijing Surveying and Mapping,2018,32(2):239-244.
[21] 傅荣林.主成分综合评价模型的讨论[J].系统工程理论与实践,2001,21(11):68-74.
FU Ronglin.Discussion of integrated evaluation models of the principal component analysis [J].Systems Engineering-Theory &Practice,2001,21 (11):68-74.
