0 引 言
现有开采沉陷理论和方法中,对地表移动稳定后的沉陷变形预计的研究较为充分且成熟,但对于地表移动随时间变化的动态过程的研究还相对不足,尤其是在动态预计精度方面还有待提高。在国内外的动态预计实践中,通常采用将静态预计模型结合相应的时间函数来实现[1-3],由于静态预计模型比较成熟,因此在动态预计中选择适宜的时间函数至关重要,它对动态预计精度的高低有重要影响。可供选择的时间函数有很多,如Sroka-Schober时间函数、广义时间时间函数、正态分布时间函数等[4-6],但我国动态预计中最常用的时间函数是Knothe时间函数。不同的时间函数在应用中各有不足,崔希民等[7-9]对Knothe时间函数进行了深入的研究,指出了该时间函数的不足,给出了理想时间函数的分布形态和5种时间系数的确定方法。黄乐亭[10]等研究了地表动态移动过程,给出了地表移动变形的3个阶段;常占强等[11]将Knothe时间函数分段表达,解决了原函数在开始阶段预计精度较低的问题。张兵等[12]指出了可用作动态预计时间函数图像必需具备的3个特征;杨泽发等[13]建立了Logistic模型与InSAR观测值之间的函数关系,然后利用InSAR观测值估计Logistic模型参数,进而再采用Logistic模型进行动态预计。张凯等[14]采用生长函数模型对正态分布时间函数进了优化,解决了其密度函数的有效积分域亏损随时间参数而减小的问题。李怀展等[15]提出了1种基于加权法和地质力学参数敏感性的地表沉降动态预测方法,并用实例证明了该方法可以提高地表动态沉降的预测精度。通过文献分析可知,现有动态沉陷预计模型较少结合足够的工程应用,多是基于纯理论,且多数模型的动态预计参数求取不易,推广应用存在困难。笔者将采用理论上相对较为完善的优化分段Knothe时间函数结合概率积分法[16-17]建立地表任意点沉降变形动态预计模型,并编制动态预计程序,为采区建筑物保护、采空区土地利用、开采损害鉴定等工作提供技术支持。
1 动态预计时间函数选择
在进行动态预计时,国内外的通用做法是:①根据工作面开采进度将工作面划分为不同的动态开采单元,单元划分采用周期来压步距法或有效尺寸分割法,其主要目的是在给定预计时刻判定对应的开采位置,进而计算每个单元采后所经历的时间;②将每个动态开采单元的静态预计结果乘以对应的时间函数,求出每个开采单元对地表沉降变形的影响值,由于在给定的预计时刻,每个单元开采后所经历的时间不同,对地表的影响并非都达到了最大值,采用时间函数的目的则是为了求出每个动态单元开采所对应的地表沉陷“不充分程度调整系数”。因此,在动态预计中时间函数的选择尤为重要,决定着动态预计结果的精度。笔者曾在分段Knothe函数的基础上,对其存在的问题进行了优化,扩展了其对于不同地质采矿条件的适应性,并通过预计实践证明了其比原Knothe时间函数具有更高的精度。即采用优化分段Konthe时间函数作为动态预计时间函数[18-19]。其函数模型见式(1),函数图像如图1所示。
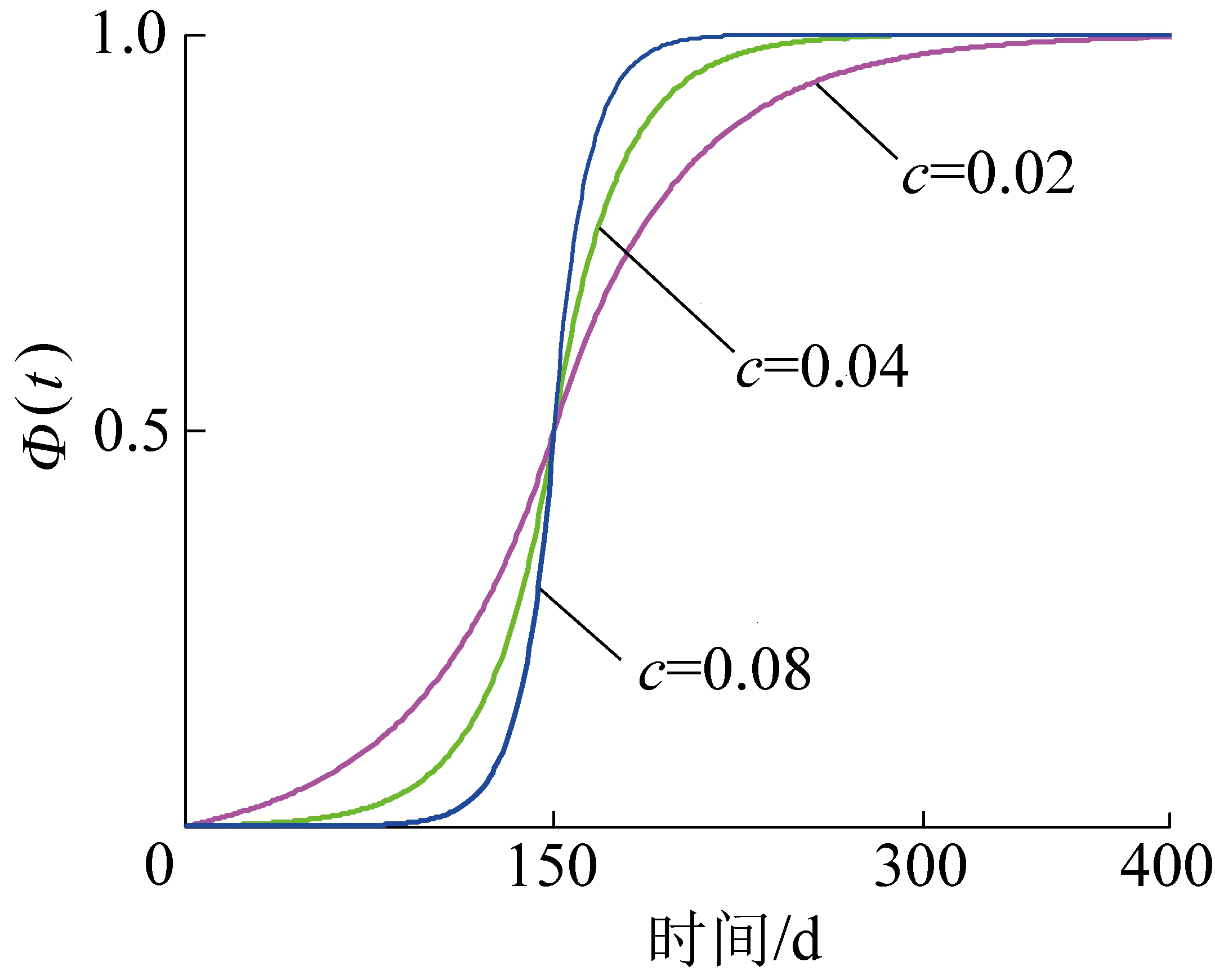
图1 优化分段时间函数图像形态
Fig.1 Figure of optimized segmented time function
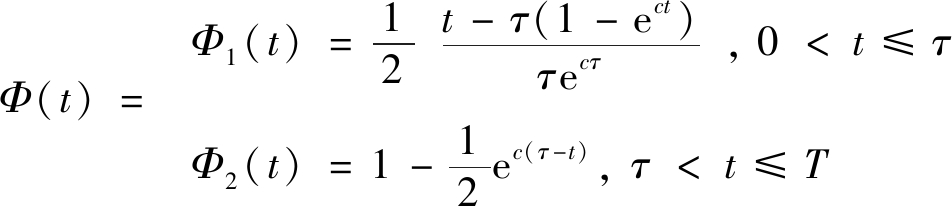
(1)
式中:Φ(t)为优化分段Knothe时间函数;Φ1(t)为分段函数第1部分;Φ2(t)为分段函数第2部分;t为预计时刻;τ为下沉速度最大值出现时刻;c为与覆岩力学性质相关的时间系数;T为地表移动总时间。
从时间函数图像可知,该时间函数符合时间函数的3个特征且曲线形态比较理想。即:①下沉初始阶段函数斜率逐渐增大,函数值在0~1变化;②在活跃期,函数值从小到大变化迅速;③在衰退期,函数斜率逐渐减小,函数值最终趋于1。
2 动态预计基本原理与模型构建
2.1 任意点沉陷预计原理
地表下沉盆地计算原理可用图2进行描述,图中xoy是地面坐标系,CO1E为煤层坐标系,v1t1、v2t2、…、vntn为划分的动态开采单元,v指每个动态单元的开采速度,t指每个动态单元的开采时间,开采单元长度按照有效尺寸分割法进行,即按0.1H0(H0为工作面平均采深)进行划分[20]。
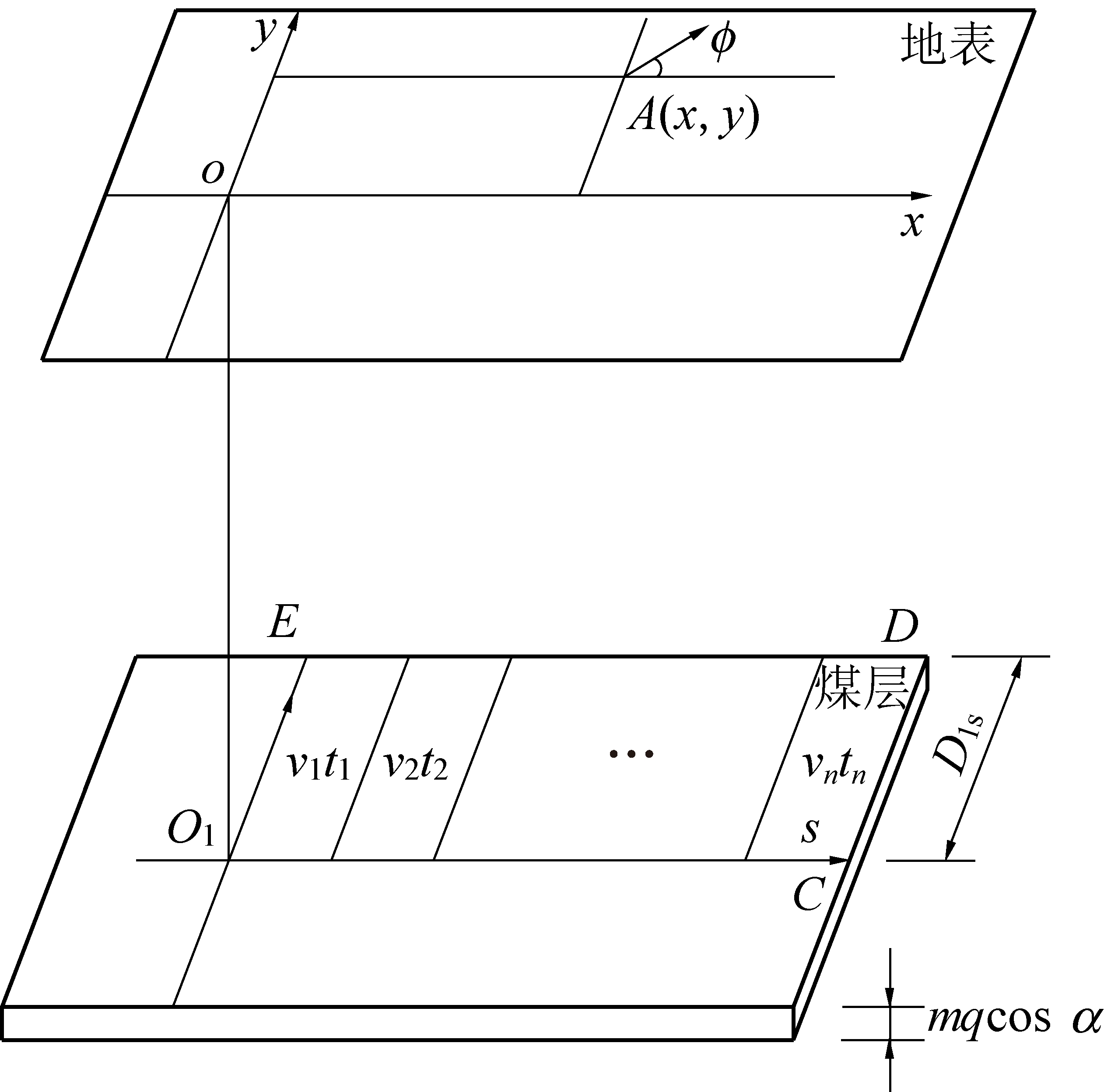
图2 水平煤层动态预计单元划分
Fig.2 Dynamic unit division of horizontal Coalseam
根据概率法原理,某一动态单元(v1t1)开采,其引起的地表任意一点A(x,y)的下沉量W(x,y)可式(2)计算[11],即
(2)
式中:W0为最大下沉量;v1t1第1个动态单元长度;D1s为工作面倾向长。
在动态预计中,由于各动态单元对地表的影响需要分别计算,因此各单元走向均为非充分开采,式(2)不能直接转换为二次积分求解,需要采用面积分的方法计算,面积分的方法有多种,如龙贝格积分法、复化梯形公式法、辛普森积分法等,本模型采用辛普森积分法实现各动态单元面积分的计算,二重积分数学求解方法相关数学文献均有详细步骤,在此不再阐述。
2.2 任意点沉陷预计模型
根据第2.1节描述的动态预计基本过程可知,在给定的预计时刻,首先需要判断此时刻所对应的工作面位置,然后判断已开采的动态单元数,进而对每个已开采单元所经历的采后时间进行确定。接着利用时间函数求取各单元对应的时间函数值。如果已开采单元经历的时间较长,其对地表的影响达到了最大,则对应的时间函数的计算结果为1,否则为0~1的数值。假设已开采的动态单元数是n,根据动态预计原理:动态预计可用动态单元静态预计结果乘以动态单元时间函数值求得[7],则任意点沉陷预计模型可用式(3)进行计算,即
W(x,y)=W1(x,y)Φ(t)(1)+W2(x,y)Φ(t)(2)+…+
Wn(x,y)Φ(t)(n)
(3)
式中:W1(x,y)是指第1个动态单元v1t1开采后对地表下沉最大影响值的计算公式,Φ(1)(t)是指第一个动态单元所对应的时间系数,采用式(1)求取,其他公式含义类比可得。
根据概率积分法原理[16]可知,各函数可用式(4)~式(9)表示,即
(4)
(5)
(6)
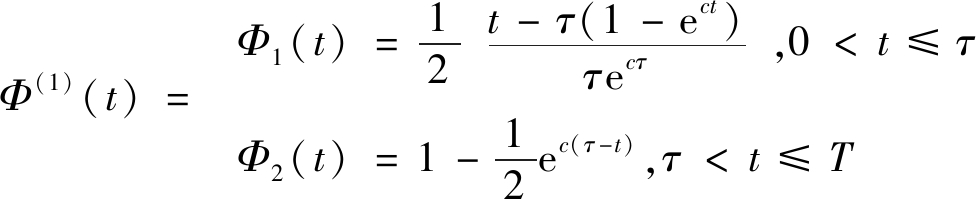
(7)
Φ(2)(t-t1)=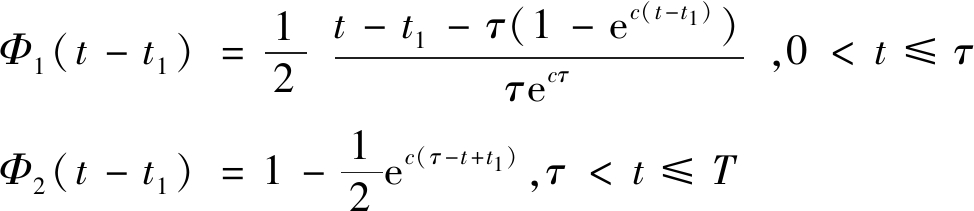
(8)
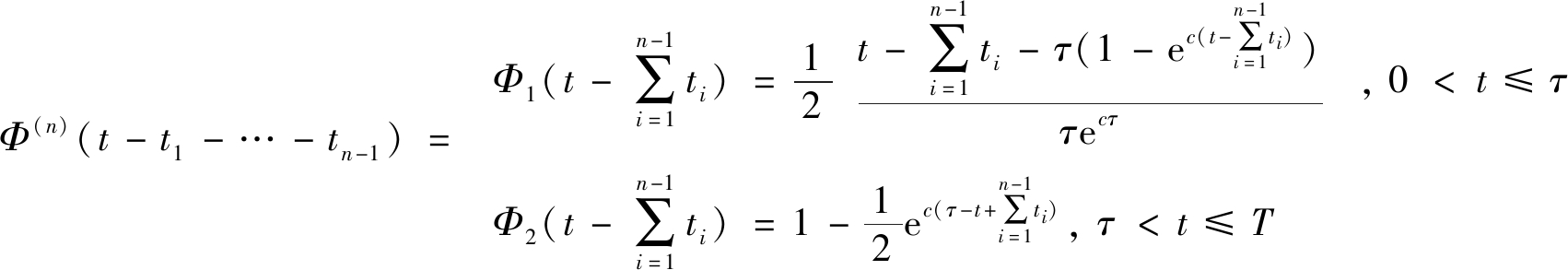
(9)
在任意点地表下沉动态预计模型中,各动态单元的开采影响直接采用概率积分模型计算,在计算最后一个动态单元vntn的开采影响时,公式(6)积分的上限不一定是vntn,可能处于vn-1tn-1~vntn的中间某一位置,具体据其在预计时刻的实际进度进行判断。在计算Φ1(t)~Φn(t-t1-…-tn-1)时,需要判断t,t-t1,…,t-t1-…-tn-1与时间函数参数τ的大小,然后确定采用时间函数的哪段公式进行计算。限于篇幅,本文仅给出地表下沉动态预计公式,地表倾斜、曲率、水平变形、水平移动等动态预计公式可根据概率积分相应公式类比得到。
3 任意点移动变形动态预计实例
3.1 预计实例1
某矿1002工作面的采矿和地质条件为:上山采深H2=279 m,下山采深H1=322 m,倾向长为250 m,走向长为1 000 m ,采高为1.45 m,下沉系数q=0.78,煤层倾角为12°,开采影响传播角θ0=81.6°,水平移动系数b1=0.36、b2=0.30,拐点偏移距为S1=30 m、S2=28 m,主要影响角正切tan β1=2.2、tan β2=2。动态预计参数为:工作面平均开采速度v为5.0 m/d,动态单元长度采用有效尺寸分割法[20],确定为0.1H0,时间函数参数τ和c按照笔者在文献[19]中所介绍的方法自动计算,动态预计程序按本文模型及算法编制。为了揭示开采过程中地表移动变形的动态发展规律,需要在不同的时刻(T)对该工作面开采过程中地表任意点的下沉和倾斜进行动态预计,将预计结果采用三维可视化图形进行显示,如图3、图4所示。

图4 不同预计时刻的地表任意点倾斜动态发展
Fig.4 Dynamic incline development of arbitrary ground surface point face at different time

图3 不同预计时刻的地表下沉盆地动态发展
Fig.3 Dynamic development of surface subsidence basin at different time
图3中下方矩形区域表示实际采面所对应的计算工作面(考虑了拐点偏距的影响),由于开采速度较小,因此地表下沉持续时间较长,图3a是在T=250 d时进行的地表下沉动态预计图 ,图3b、图3c、图3d分别是在T=400、550、900 d进行的地表下沉动态预计图,由图3可知,随开采时间的增加,地表移动盆地范围逐渐朝工作面开采方向扩展,当T=900 d时,工作面的开采影响达到了最大,此时地表已处于稳定状态,此后再增加T值,地表下沉的范围将维持不变。从工作面的开采情况可知,当工作面开采完毕之后,其走向为充分采动,理论上其拐点处的下沉量应为下沉盆地最大值的1/2,根据定义,图3中坐标(x,y)为:(0,75)和(900,75)两点即为下沉曲线的拐点,预计结果显示,地表移动盆地的最大下沉量为1 280.6 mm,而2个拐点的下沉量前者为641.1 mm,后者为634.4 mm,2个拐点的下沉量基本接近理论值的 1/2,从理论上证明了本文所建模型的可靠性。
图4是在不同的预计时刻计算得到的地表任意点倾斜动态发展变化,同样,随预计时间的增加,地表的倾斜也是不断的向开采方向发展,当T=900 d 地表移动稳定时,地表倾斜三维图形成了符号相反的对称图形,此时中间平底部分的倾斜均为0,由其发展过程可知,中间倾斜值为0的地表点也是经历了从小到大,再从大到小,最后为0的剧烈变化过程,如果只进行稳定后的静态预计则反映不了这个动态过程。
3.2 预计实例2
钱家营矿1176东工作面相应的概率积分参数如下,倾向长 160 m,走向长 1 015 m,煤层厚度2.9 m,煤层倾角8°,下山采深474 m,上山采深 454 m,下沉系数q为0.96,上山主要影响角正切值为1.9,下山主要影响角正切值为2.1,开采影响传播角为84.4°,拐点偏距为24 m,平均开采速度为2.5 m/d。
该工作面设置了2条观测线,其中东线设有30个测点,在1999年4月22日至2001年10月1日共观测了18次。测点和工作面位置关系如图5所示,X、Y为大地坐标。为了对比方便,首先对实测数据进行处理,得到各次观测实测下沉量如图6所示,由于该工作面所布设观测线既不在走向主断面上,也不在倾向主断面上,因此,在进行动态预计时,需要预计全盆地地表下沉,然后再提取监测点下沉数据。预计的下沉量如图7所示。
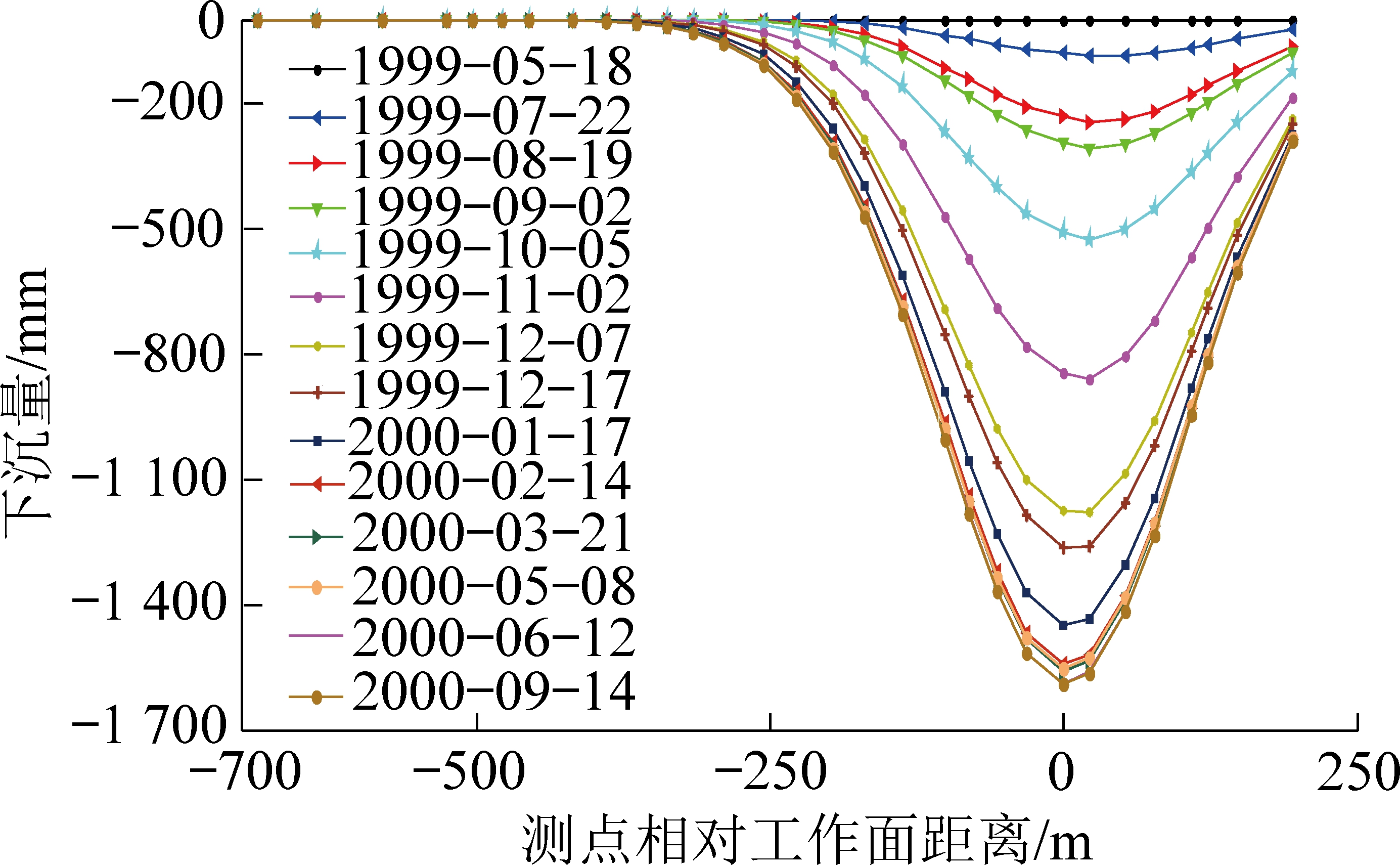
图7 观测点预计下沉曲线
Fig.7 Predicted subsidence curves of monitoring points
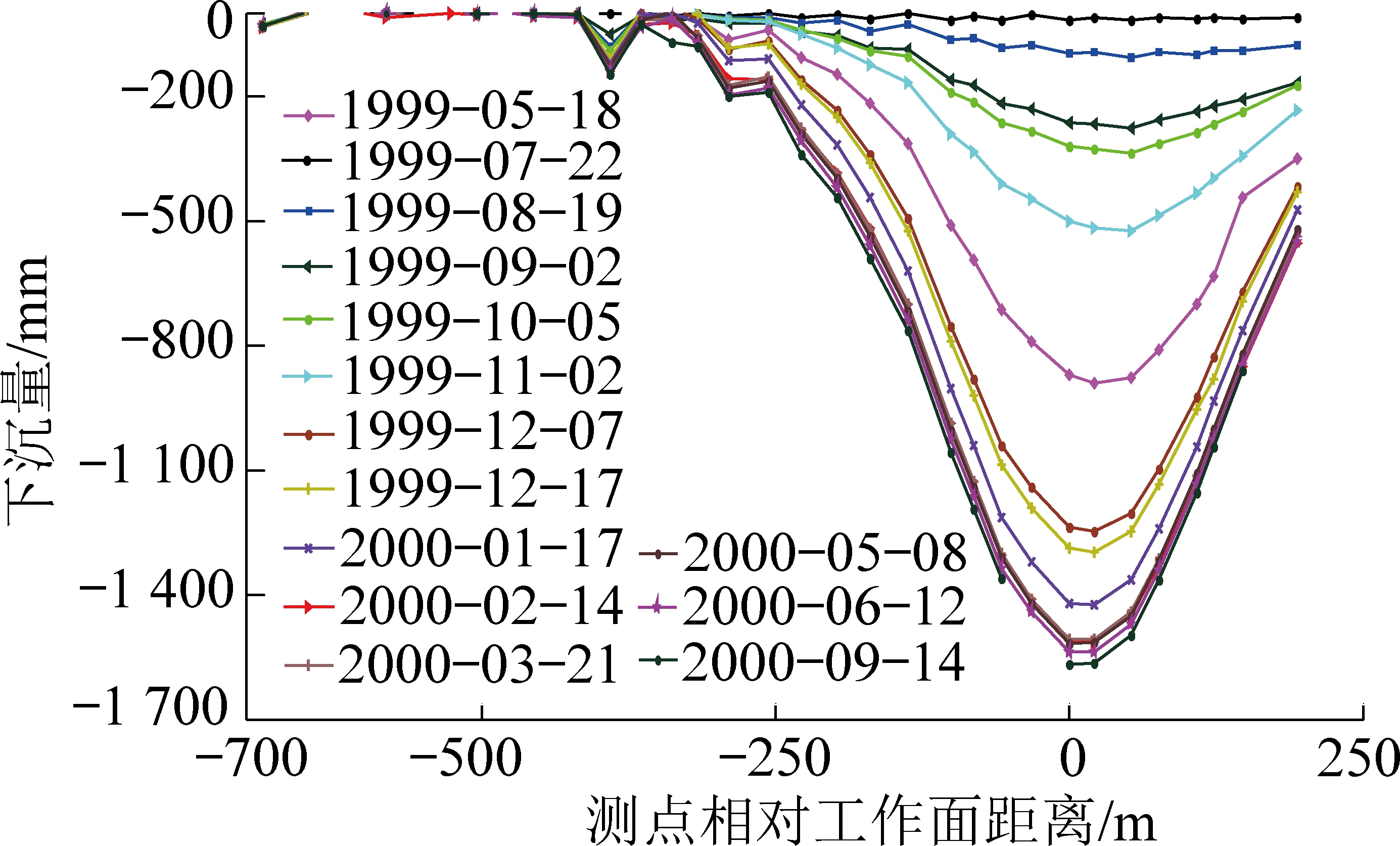
图6 观测点实测下沉曲线
Fig.6 Measured subsidence curves of monitoring point
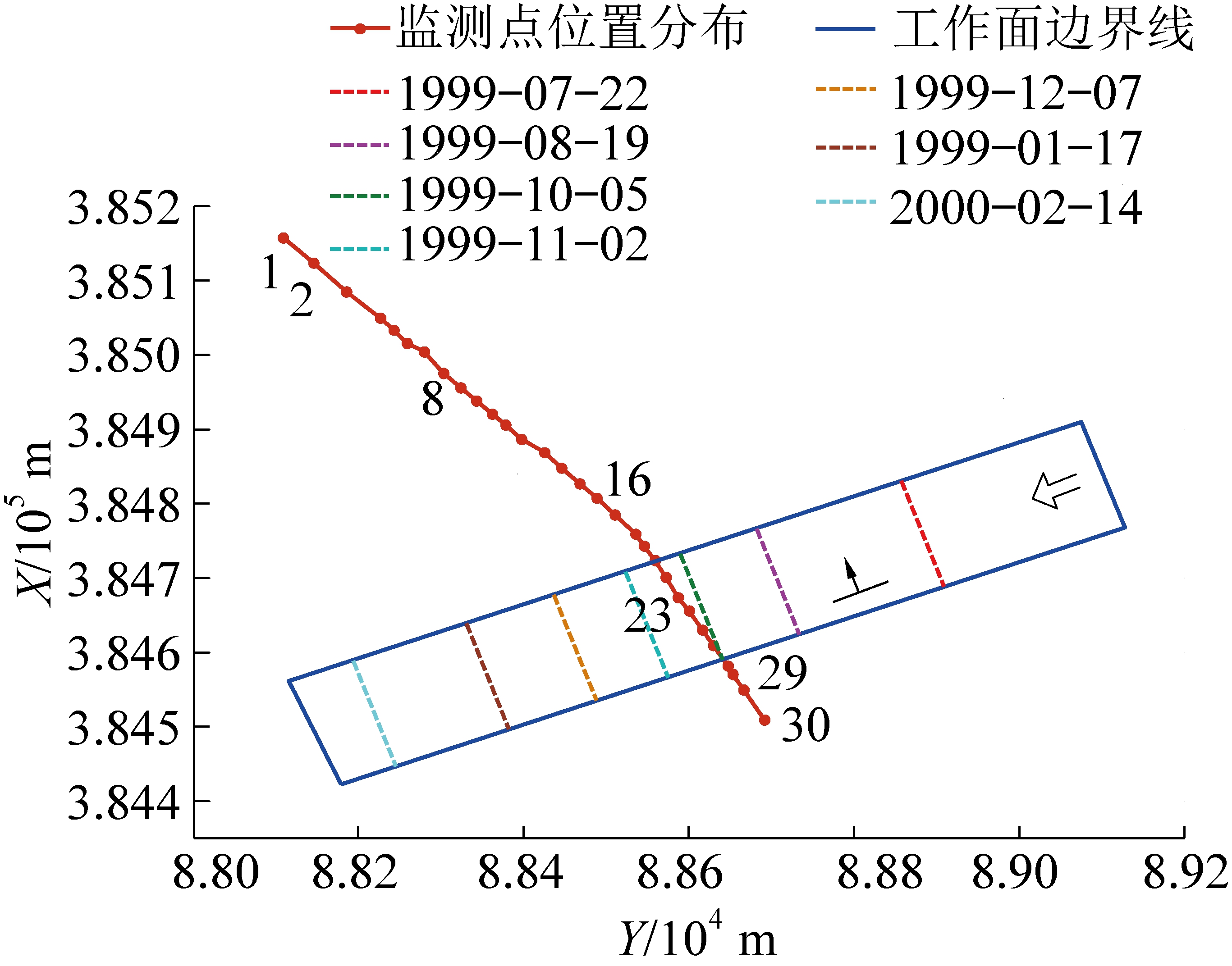
图5 测点与工作面相对位置关系
Fig.5 Relative position of monitoring point and working face
为了更好地比较预计结果和实测结果,下面抽样选取第3、5、7、9、11、14次观测结果和预计结果进行对比分析,对比如图8所示。
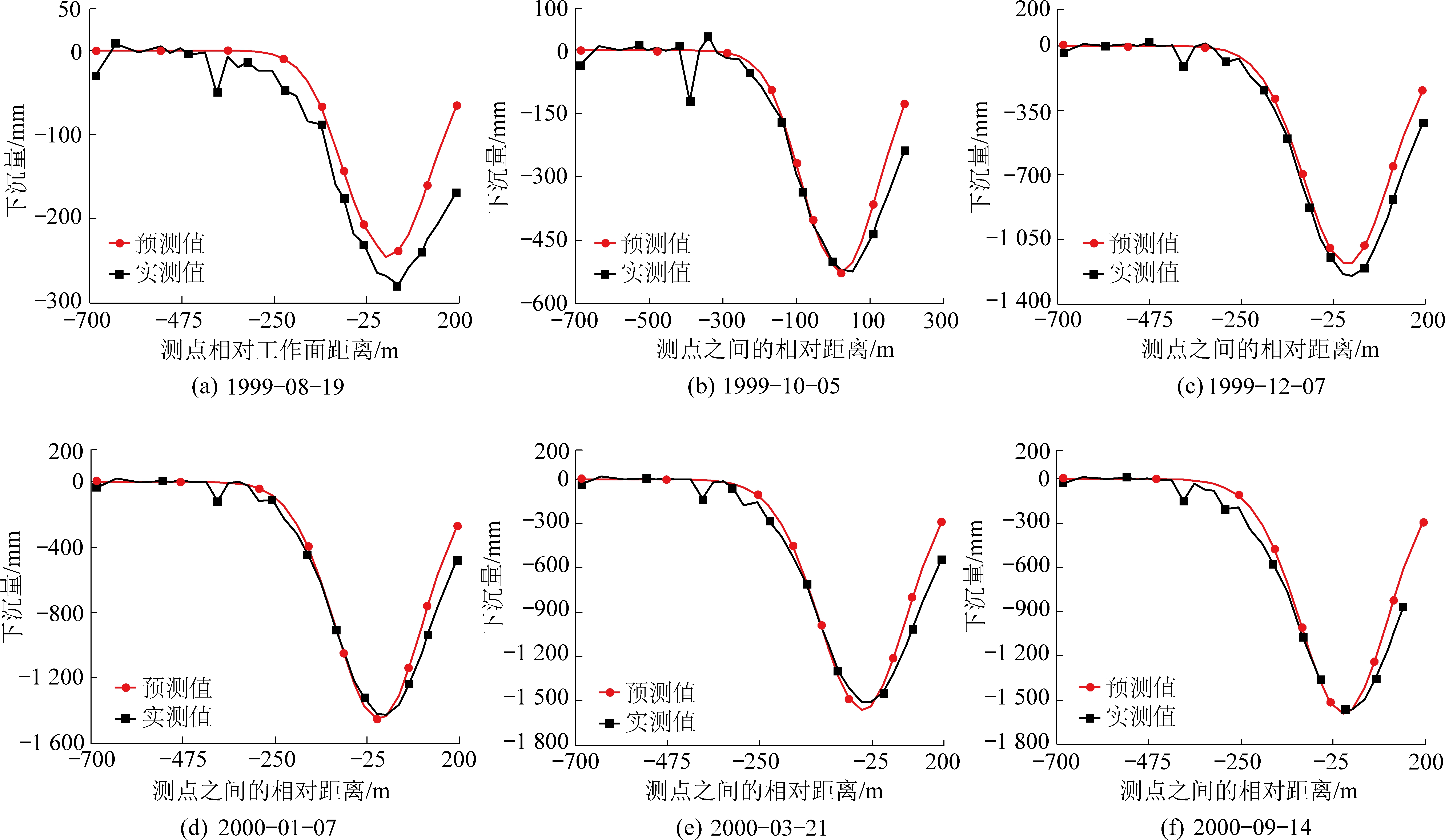
图8 抽样实测结果和动态预计结果对比
Fig.8 Comparison between measured results and dynamic prediction results of samplings
抽样对比预测与实测数据,并进行预测中误差和相对误差计算,计算方法可参考文献[12]。计算后得到的误差统计见表1。由表1知,预测误差中最小是±39.7 mm,最大是±101.3 mm,预测的相对误差最小是5.6%,最大是14.2%,第3期预测和实测相对误差较大,为14.2%,在随后的动态预测中,相对误差逐渐减小,最终维持在6.5%左右,综合来看,利用所建模型进行动态预测,预测相对误差可控制在8%左右。
表1 预测误差统计(抽样)
Table 1 Prediction error statistics(sampling analysis)

观测时间预测下沉量中误差/mm最大值/mm相对误差/%观测时间预测下沉量中误差/mm最大值/mm相对误差/%1999-08-19(第3次)±39.727914.22000-01-07(第9次)±8014255.61999-10-05(第5次)±43.15248.22000-03-21(第11次)±97.415076.51999-12-07(第7次)±85.112796.82000-09-14(第14次)±101.315686.5
4 结 论
1)以概率积分法为基础,采用优化分段Knothe时间函数,构建了煤炭开采过程中地表任意点动态沉降变形预计模型。根据计算模型开发了预计程序,能够方便提取走向和倾向主断面上的点的移动变形值,对于所关注的任何点位也都能够做到方便的提取和精确的预测,同时还实现了预计结果的实时三维显示。
2)对某矿1002工作面开采进行动态预计的结果表明:地表下沉盆地2个拐点的下沉值基本等于盆地最大下沉值的1/2,这与理论所揭示的规律是相符的,证明了所建模型的可靠性。
3)通过对钱家营矿1176东工作面开采进行动态预计表明:预测中误差最大为101.3 mm,最小为39.7 mm,预测相对中误差最大为14.2%,最小为5.6%,综合来看,预测相对中误差可维持在8%左右,精度较高,能够满足矿区绝大多数工程建设的需要。
参考文献(References):
[1] GONZALEZ Nicieza C,ALVAREZ-Fernandez M I,MENENDEZ-Diaz A,et al.The influence of time on subsidence in the Central Asturian Coalfield[J].Bulletin of Engineering Geology and the Environment,2007,66(3):319-329.
[2] 胡青峰,崔希民,康新亮,等.Knothe时间函数参数影响分析及其求参模型研究[J].采矿与安全工程学报,2014,31(1):122-126.
HU Qingfeng,CUI Ximin,KANG Xinliang,et al.Impact of parameter on Knothe time function and its calculation model[J].Journal of Mining &Safety Engineering,2014,31(1):122-126.
[3] HAN Haoliang,CUI Bo.Modeling of surface subsidencebased on time function[J].Advanced Materials Research,2011,422:318-321.
[4] 彭小沾,崔希民,臧永强,等.时间函数与地表动态移动变形规律[J].北京科技大学学报,2004,26(4):341-344.
PENG Xiaozhan,CUI Ximin,ZANG Yongqiang,et al.Time function and prediction of progressive surface movements and deformations[J].Journal of University of Science and Technology Beijing,2004,26(4):341-344.
[5] KOWALSKI A.Surface subsidence and rate of its increments based on measurements and theory[J].Archives of Mining Science,2001,46(4):391-406.
[6] 李春意,高永格,崔希民.基于正态分布时间函数地表动态沉陷预测研究[J].岩土力学,2016,37(S1):108-116.
LI Chunyi,GAO Yongge,CUI Ximin.Progressive subsidence prediction of ground surface based on the normal distribution time function[J].Rock and Soil Mechanics,2016,37(S1):108-116.
[7] 崔希民,缪协兴,赵英利,等.论地表移动过程的时间函数[J].煤炭学报,1999,24(5) :453-455.
CUI Ximin,MIAO Xiexing,ZHAO Yingli,et al.Discussion on the time function of time dependent surface movement[J].Journal of China Coal Society,1999,24( 5):453-455.
[8] 刘玉成,曹树刚,刘延保.改进的Konthe 地表沉陷时间函数模型[J].测绘科学,2009,34(5) :16-31.
LIU Yucheng,CAO Shugang,LIU Yanbao.The improved Knothe time function for surface subsidence[J].Science of Surveying and Mapping,2009,34( 5) :16-31
[9] 王军保,刘新荣,刘小军.开采沉陷动态预测模型[J].煤炭学报,2015,40(3):517-521.
WANG Junbao,LIU Xinrong,LIU Xiaojun.Dynamic prediction model for mining subsidence[J].Journal of China Coal Society,2015,40(3):517-521.
[10] 黄乐亭,王金庄.地表动态沉陷变形的3个阶段与变形速度的研究[J].煤炭学报,2006,31(4):420-424.
HUANG Leting,WANG Jinzhuang.Study on the three stages and deformation velocity of dynamic surface subsidence deformation[J].Journal of China Coal Society,2006,31(4):420-424.
[11] 常占强,王金庄.关于地表点下沉时间函数的研究—改进的克诺特时间函数[J].岩石力学与工程学报,2003,22(9):1496-1499.
CHANG Zhanqiang,WANG Jinzhuang.Study on time func- tion of subsidence:the improved Knothe time function [J].Chinese Journal of Rock Mechanics and Engineering,2003,22(9):1496-1499.
[12] 张 兵,崔希民,胡青峰.开采沉陷动态预计的正态分布时间函数模型研究[J].煤炭科学技术,2016,44(4):140-145.
ZHANG Bing,CUI Ximin,HU Qingfeng.Study on normal distributed time function model to dynamically predict mining subsidence [J].Coal Science and Technology,2016,44(4):140-145.
[13] YANG Zefa,LI Zhiwei,ZHU Jianjun.Deriving dynamic subsidence of coal mining areas using InSAR and Logistic Model[J].Remote Sensing,2017,(9):125-144
[14] 张 凯,胡海峰,廉旭刚,等.地表动态沉陷预测正态时间函数模型优化研究[J].煤炭科学技术,2019,47(9):235-240.
ZHANG Kai,HU Haifeng,LIAN Xugang,et al.Optimization of surface dynamic subsidence prediction normal time function model[J].Coal Science and Technology,2019,47(9):235-24.
[15] LI Huaizhan,ZHA Jianfeng,GUO Guangli.A new dynamic prediction method for surface subsidence based on numerical model parameter sensitivity[J].Journal of Cleaner Production,2019,233:1418-1424.
[16] 何国清,杨 伦,凌赓娣,等.矿山开采沉陷学[M].徐州:中国矿业大学出版社,1997.
[17] 郭增长,柴华彬.煤矿开采沉陷学[M].北京:煤炭工业出版社,2013.
[18] 张 兵,崔希民.开采沉陷动态预计的分段Knothe时间函数模型优化[J].岩土力学,2017,38(2):541-547,556.
ZHANG Bing,CUI Ximin.Optimization of segmented Knothe time function model for dynamic prediction of mining subsidence [J].Rock and Soil Mechanics,2017,38(2):541-547,556.
[19] 张 兵,崔希民,赵玉玲,等.优化分段 Knothe 时间函数求参方法[J].煤炭学报,2018,43(12):3379-3386.
ZHANG Bing,CUI Ximin,ZHAO Yuling,et al.Parameter calculation method for optimized segmented Knothe time function [J].Journal of China Coal Society,2018,43(12):3379-3386.
[20] 吴 侃,靳建明.时序分析在开采沉陷动态参数预计中的应用[J].中国矿业大学学报,2000,29(4):413-415.
WU Kan,JIN Jianming.Prediction of dynamic mining subsidence parameters by time series analysis method[J].Journal of China University of Mining &Technology,2000,29(4):413-415.
