0 引 言
采空区是地下开采空间围岩失稳产生位移、开裂、破碎垮落，直至上覆岩层整体下沉、弯曲引起的地表变形和破坏，其场地稳定性涉及地形、地质、采矿等诸多复杂影响因素[1]。开展采空区场地稳定性评价研究是连接采空区勘察和治理的重要环节，是保证采空区地面建设安全的前提，具有重要实际意义。在采空区上方开展建设面临采空区隐伏性强、空间分布特征规律性差、采空区顶板冒落塌陷情况难以预测等问题，对这类采空塌陷场地进行稳定性评价复杂性与“噪声”的多样性大幅增加[2-3]。已完成的采空区场地稳定性评价大多采用《煤矿采空区岩土工程勘察规范》(以下简称《规范》)推荐的煤(岩)柱稳定分析法，开采条件判别法，地表移动变形判别法等方法进行评价，综合采空区类型、开采方法及顶板管理方式、终采时间、地表移动变形等采空区变形特征，以定性和定量相结合的方法划分采空区场地稳定性[4]。然而，实际采空区场地稳定性是地质采矿因素相互影响的复杂动态过程，不同类型的采空区地表移动变形特征的影响因素不尽相同，《规范》给出了采空区场地稳定性评价的主要影响因素，但没有明确的综合判别准则，使得这些稳定性评价方法使用难度较高，局限性大[5]。
对反映采空区场地稳定性的多属性影响因素进行数据搜集和统计观测，多因素、大样本数据在为研究采空区场地稳定性提供丰富信息的同时，许多变量之间的相关性，增加了分析问题的复杂程度：若分别对样本中每个指标进行分析，结果往往孤立；盲目减少指标又会损失信息，产生错误结论[6]。当前，随着机器学习理论与人工智能技术的发展，卷积神经网络(convolution neural network,CNN)、支持向量机(support vector machine,SVM)、模糊聚类分析等非线性机器学习理论在采空区场地稳定性研究中取得了成功应用。刘志祥等[7]通过建立的PCA-SVM模型对某金属矿采空区的危险性进行判别，判别结果与实际采空区危险性情况相符；丁陈建[8]以终采时间、沉降趋势、深厚比等作为影响因子，建立3层BPNN模型，并利用模糊综合评价结果对网络模型进行训练、检验；李爱兵[9]探讨了SVM回归模型在采空区稳定性评价应用的可行性；层次分析法(AHP)[10]根据影响因子的权重集合与模糊评价矩阵来完成采空区场地模糊综合评价；模糊聚类方法[11]应用在采空区场地稳定性评价中是通过设定聚类数目和参数，给出初始隶属度矩阵，通过迭代计算新的聚类中心与隶属度矩阵，但该方法在表征稳定性的泛化能力和评价精度方面还有待提高。
主成分分析作为非监督学习的降维方法主要用来减少数据集的维度，通过方差衡量信息量以消除原始数据成分间的相互影响因素[12]。其建模过程仅需对特征值分解，通过构造正交矩阵实现数据降维，实现用少量指标描述数据特性，能有效地降低模糊聚类的计算复杂度。鉴于主成分分析方法在数据分析及特征提取的优势，结合采空区场地稳定性特点，提出一种基于该方法的采空区场地稳定性评价新思路，建立基于改进模糊聚类算法的稳定性评价新方法。
1 降维模糊C均值聚类算法理论
1.1 主成分分析(PCA)方法
主成分分析的基本思想是将样本数据原有的n维特征重构为k(k<n)维全新的正交特征(即主成分)，通过求解样本集的协方差矩阵的前n′个特征值对应的特征向量矩阵得到输出样本集，实现降维目的[13]。以降维后的主成分贡献率表征携带原始特征变异信息的大小，贡献率越大则表明主成分对原始特征信息的解释能力更强[14]。
对于煤矿采空区场地稳定性的多属性影响因素，主成分分析的具体步骤是：设m个n维样本数据(x(1),x(2),…,x(m))进行标准化预处理，经过投影变换得到的新坐标系为w={w1,w2,…,wn}，其中wi是标准正交基，即
将数据从n维降到n′维后新的坐标系为{w1,w2,…,w′n}，样本点x(i)在n′维坐标系中的投影为：
其中，
是x(i)在低维坐标系里第j维的坐标。将数据集从n维降到n′维时，需要找到最大的n′个特征值对应的特征向量。这n′个特征向量组成的矩阵W即为标准正交量w组成的主成分矩阵。对于任意一个样本x(i)，在新坐标系中的投影方差为WTx(i)x(i)TW，从最大可分性出发，使所有样本的投影方差之和最大，利用拉格朗日函数可以得到
J(W)=tr(WTXXTW+λ(WTW-I))
(1)
其中，X是全部样本x(i)代数和的矩阵，对主成分矩阵W求导整理后即
XXTW=-λW
(2)
对协方差矩阵XXT进行特征值分解，将求得的特征值进行排序：λ1≥λ2≥…≥λd，d为特征值个数，W=(w1,w2,…,wn′)为WT的n′个特征值对应的特征向量组成的矩阵，即为主成分分析的解。通过主成分降维，在减少分析指标的同时减少原本具有较强模糊性的非结构化数据包含的信息损失，即可实现较少的综合指标归纳存在于各变量中的各类信息。
1.2 改进模糊C均值聚类算法
基于目标函数的模糊C均值聚类算法通过对无标记训练样本的学习来揭示数据的内在性质及规律，算法提供了区别于k均值聚类算法(K-means clustering algorithm)的更加灵活的聚类结果[15]。假定数据集为X，将数据划分成c类，对应的c个类中心为C，每个样本xj属于某i类的隶属度为uij，定义模糊C均值聚类的目标函数J为[16-17]
(3)
式中：N为样本数量，M为隶属度因子；Ci为i的类中心；xj为第j个具有n′维特征的样本。目标函数由相应样本的隶属度与该样本到各个类中心的距离相乘组成。隶属度uij与聚类中心Ci的迭代式为
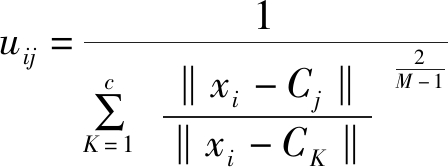
(4)
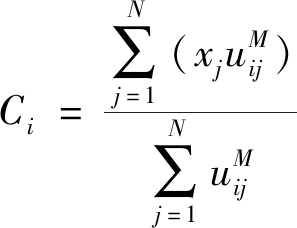
(5)
更新当前均值向量后，不断重复上述过程，迭代的终止条件为
(6)
式中：K为迭代步数；ε为误差阈值。
当继续迭代下去隶属度不发生较大变化时，即认为隶属度已达到较优状态，该过程收敛于目标函数J的局部最小值或鞍点，得到最终的类(簇)划分。可以看出uij和Ci相互关联彼此包含，在算法初始时既没有uij也没有Ci，先自赋值给其中一个变量开始迭代，通过uij和Ci不断迭代更新，目标函数J逐渐趋向稳定状态，当J不再变化时，算法收敛到较好的解。这个状态下的uij和Ci值就是最终的隶属度矩阵和聚类中心。改进的模糊C均值聚类算法流程如图1所示。
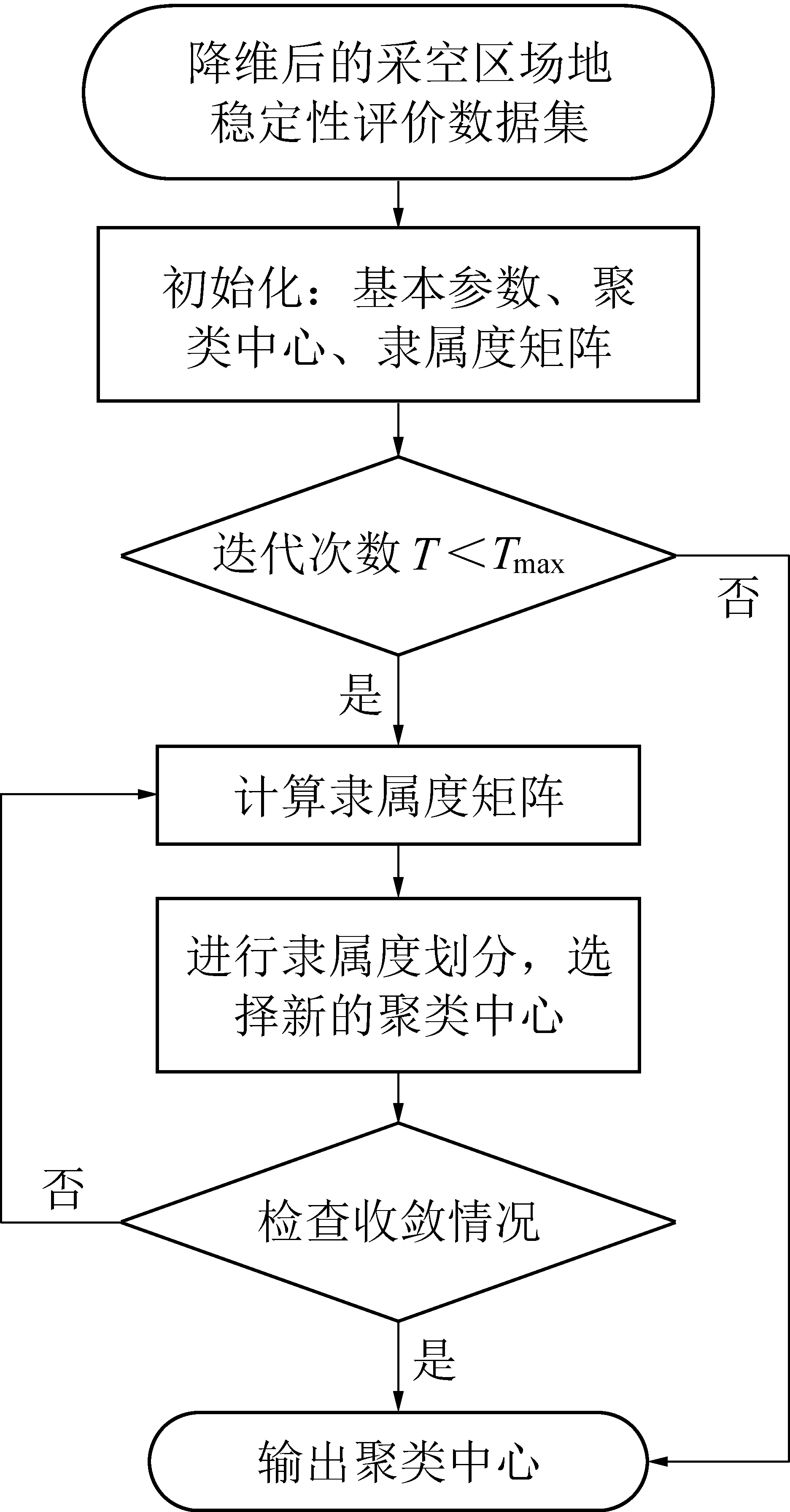
图1 改进的模糊C均值算法流程
Fig.1 Flow chart of improved fuzzy C-means clustering algorithm
2 主成分降维的模糊聚类模型
2.1 采空区场地稳定性评价指标体系构建
采空区场地稳定性影响因素主要考虑自然地质、采矿和时间3个方面[18-20]，分为矿层埋藏几何条件(矿层厚度、倾角、埋藏深度、松散层厚度、断层密度、裂隙密度)、覆岩力学性质(岩性、涨缩性及水化性)、水文性质(地下水位、煤柱被水解和软化程度、被风化程度)、采空区几何条件(采出量、采厚、采空区及巷道尺寸)、采掘技术(顶板管理、重复采动)和残余移动变形[21]等。结合山东省济宁市快速路任兴路K0+807～K6+867段地质采矿条件与资料建立采空区场地稳定性评价指标体系。该路段压覆某矿北翼二、四采区部分工作面采空区，为便于统计和全面描述快速路及其附近区域的开采沉陷与变形因素，将采空区场地稳定性评价范围扩展至道路中心线两侧外各300 m，该矿北翼二、四采区部分工作面采空区与拟建快速路相对位置关系如图2所示。
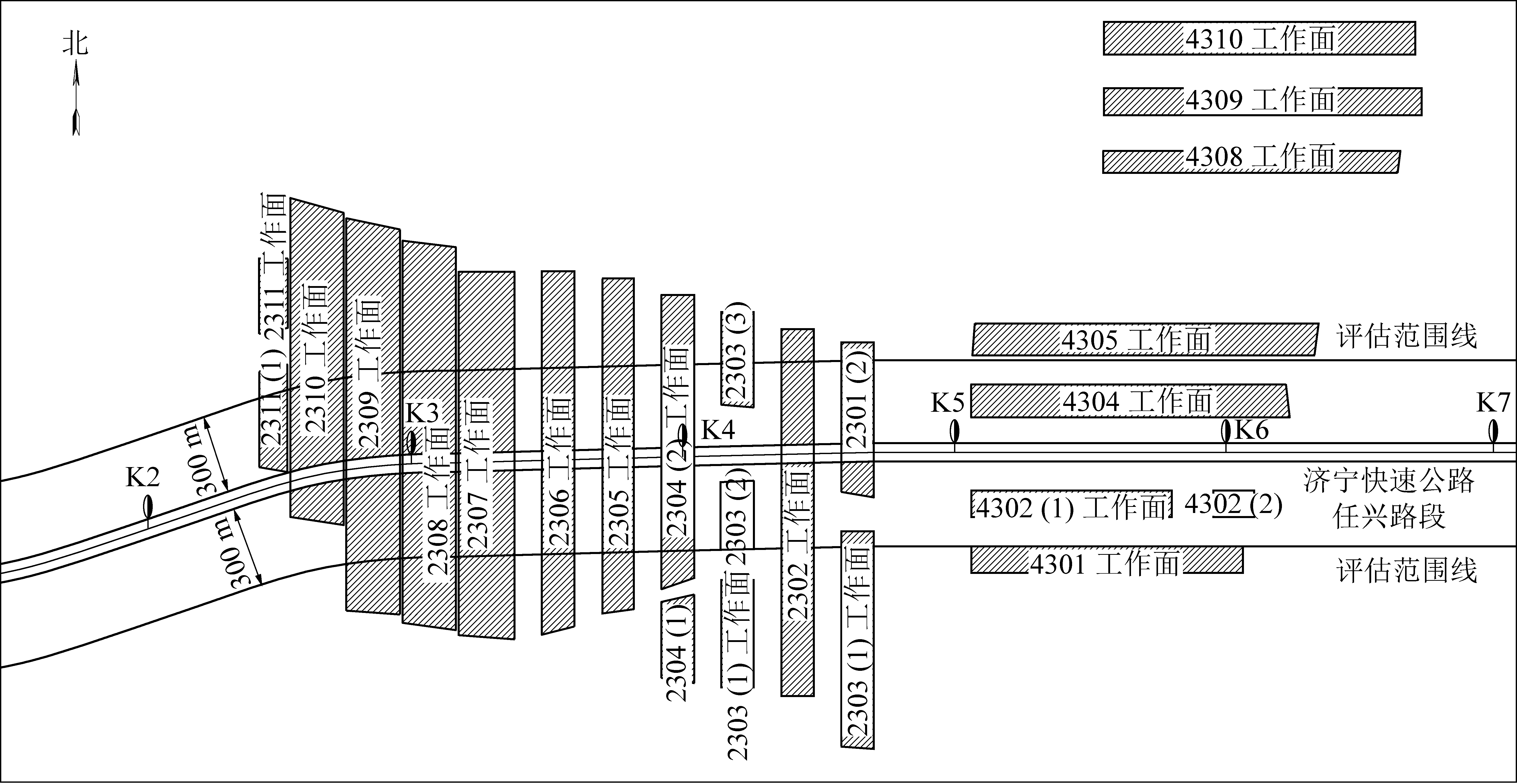
图2 工作面采空区与拟建快速路相对位置
Fig.2 Relative location between goaf section and proposed expressway
考虑到影响因素取舍更全面，从拟建快速路与压覆各工作面采空区相对位置关系、快速路范围内地质采矿条件与下伏采空区情况3个方面选取了7个指标构建采空区场地稳定性评价体系，并以这些指标的统计观测数据作为模型的输入参数，进行降维分析，具体评价指标：X1为采厚，m；X2为采深范围，m；X3为煤层倾角，(°)；X4为工作面走向长度，m；X5为距离快速路最近距离，m；X6为停采年限，a；X7为顶板管理方法。
结合采空区场地稳定性评价相关规范中采空区场地稳定性的等级划分，综合各因素之间的影响，将采空区场地稳定性等级分为4级：稳定(Ⅰ级)、基本稳定(Ⅱ级)、欠稳定(Ⅲ级)、不稳定(Ⅳ级)，对应等级的数学表达作为模型的输出参数。
2.2 稳定性影响因素的主成分降维
按照主成分分析算法步骤，输入的多属性数据经过标准化处理后的样本见表1，经标准化后的样本数据可加快模型的收敛速度，去除参数之间的量纲化。
表1 标准化后的指标样本
Table 1 Standardized index sample
样本X1X2X3X4X5X6X71-0.57070.34991.6841-1.0540-0.2000-1.4193-0.04752-0.61170.17491.6841-0.6816-0.9247-1.3370-0.04753-0.4888-0.03331.6841-1.8410-0.9247-1.4345-0.0475︙︙︙︙︙︙︙︙1204.22781.8329-0.05100.55610.2231-2.14883.2130
考虑到主成分对数据空间维数与损失信息的相关性，经主成分降维后前4个主成分的累计贡献率为81.86%，如图3所示。
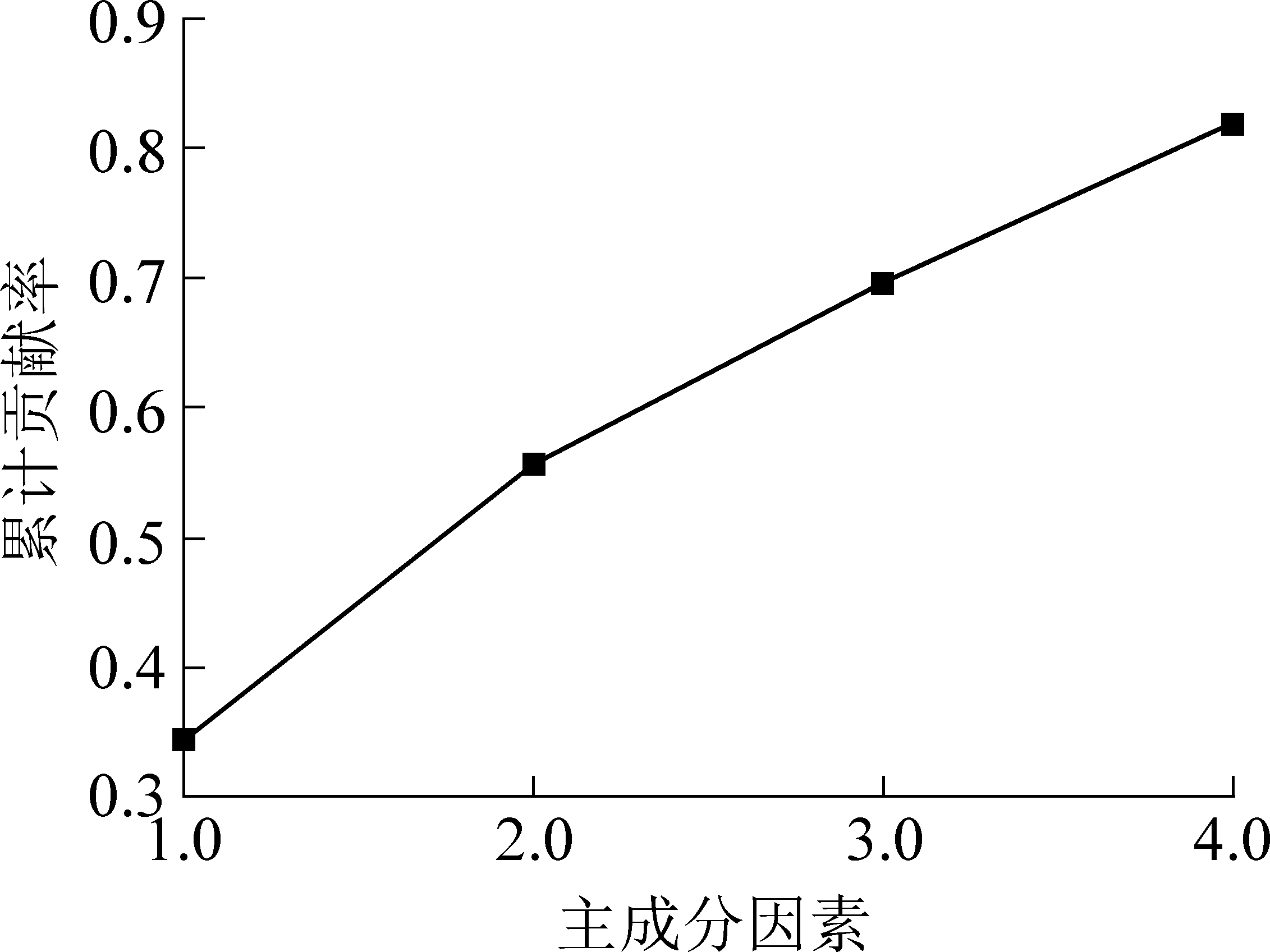
图3 主成分累计贡献率
Fig.3 Cumulative contribution rate of principal components
各主成分贡献率从大到小依次为0.344 3，0.212 6，0.139 5，0.122 2，如图4所示。可以看出，降维后的前4个主成分有较好的表征原始样本的解释能力，以这4个主成分特征作为输入参数，建立模糊C均值聚类模型。
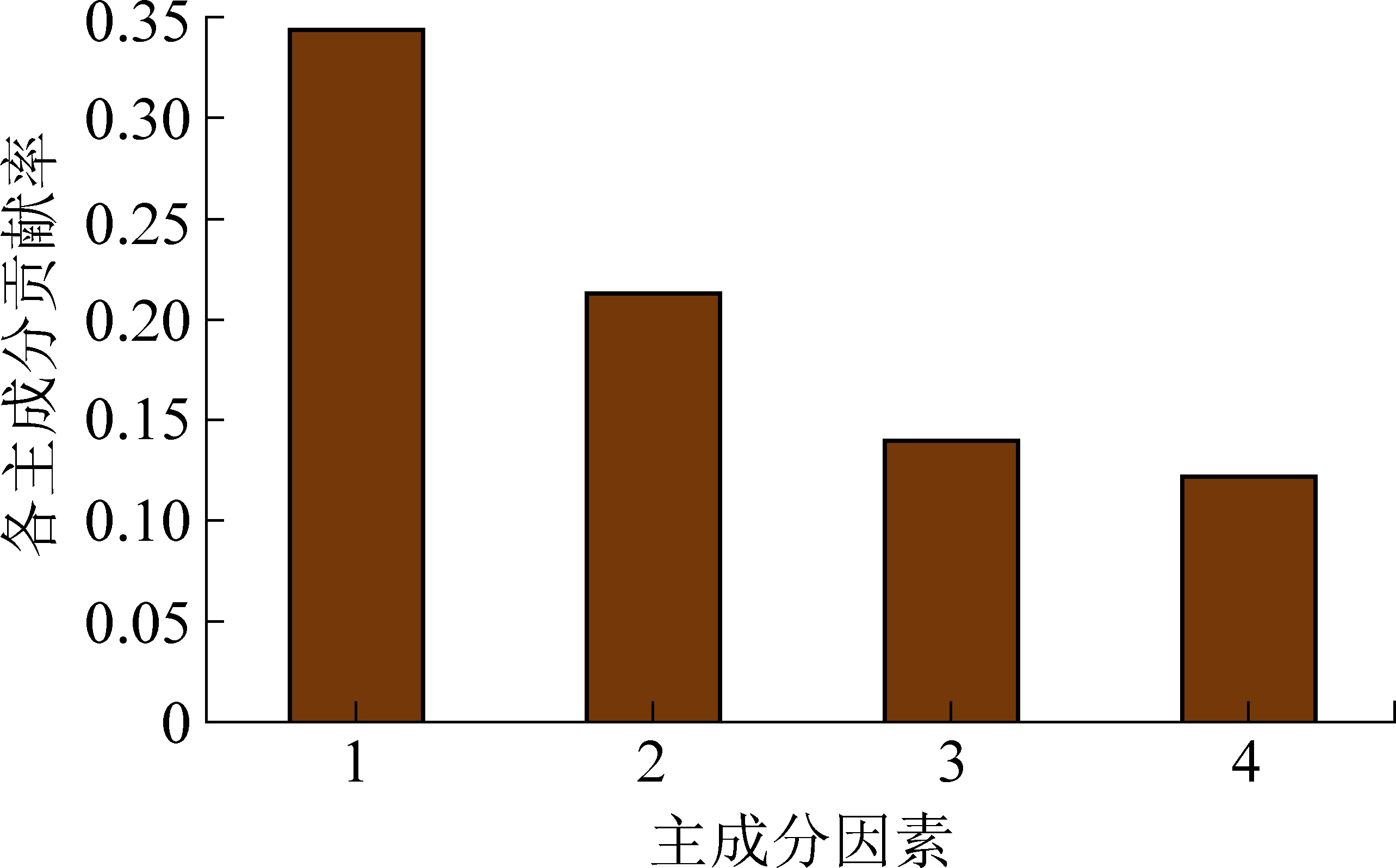
图4 各主成分贡献率
Fig.4 Contribution rate of principal components
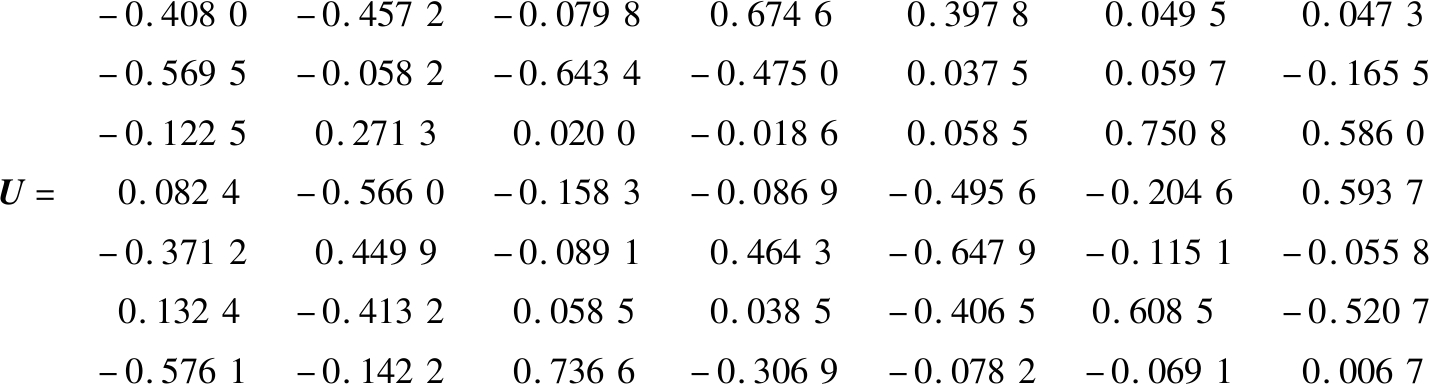
由标准化后的指标样本建立协方差矩阵X，其特征值λ1,λ2,…,λ7分别为2.447 1，1.501 2，0.234 7，0.406 8，0.643 9，0.973 3，0.856 0。对应特征值分解后的特征向量u1,u2,…,u7构成的投影矩阵为U，即
3 模糊C均值聚类效果分析
将降维后的4个主成分样本作为输入参数，采空区场地稳定性等级的数学表达作为输出参数进行模糊C均值聚类。其中，地下开采工作面采空区样本个数N=120，聚类数目为4类(c=4)，模型最大迭代数为100，模糊隶属因子M=2，聚类中心与每个样本间的欧式距离(2-范数)p=2。经初始化模糊矩阵U计算聚类中心点，同时更新隶属度得到模糊聚类的特征效果如图5所示。从图中可以看出，经过迭代更新，得到最终的四类(簇)划分，聚类中心能较好表征每1分类(簇)的特征。
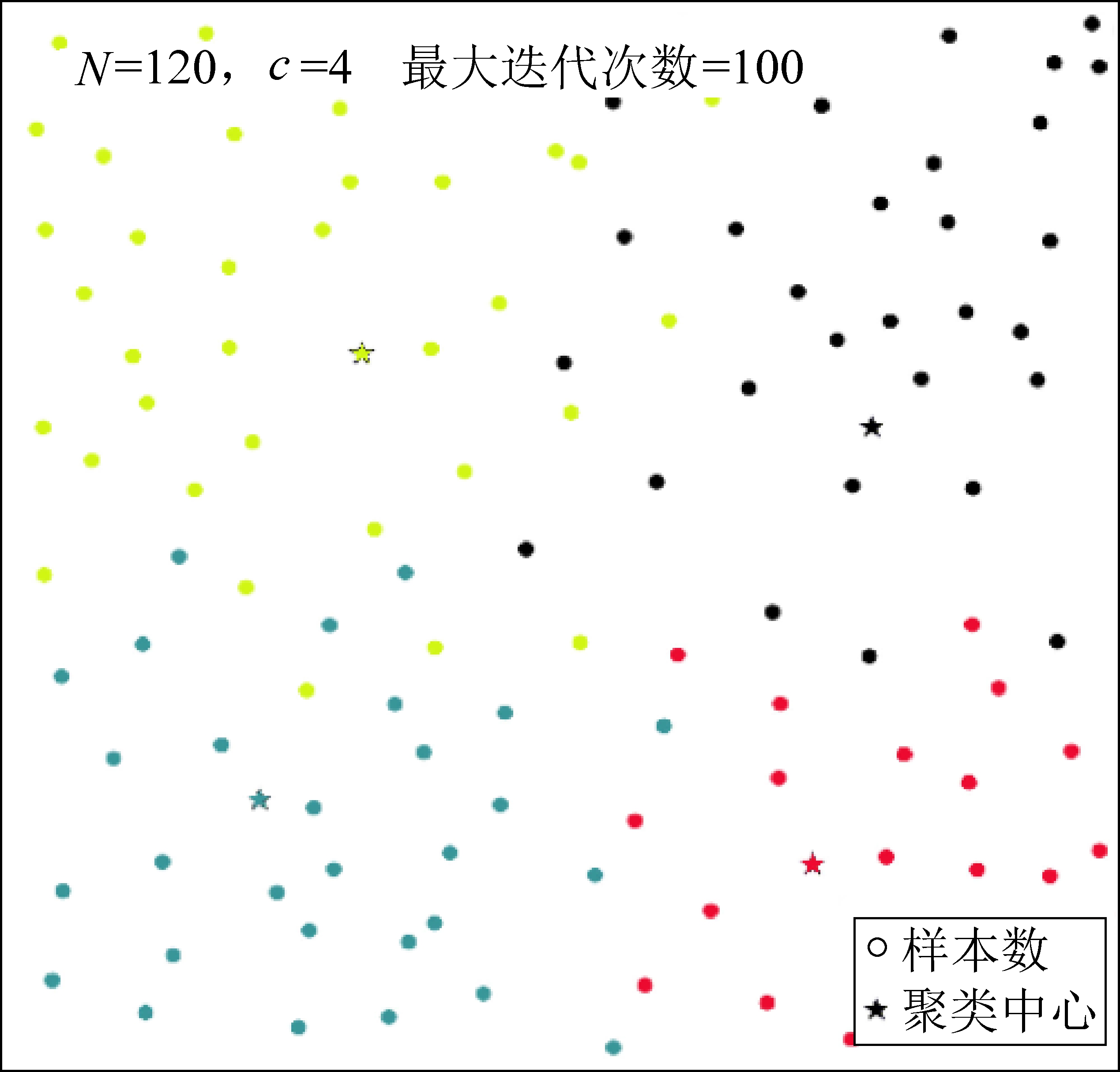
图5 模糊C均值聚类效果
Fig.5 Effect of fuzzy C-means clustering features
对4个分类(簇)中心坐标和各类(簇)样本集占比进行统计分析，可以看出：经降维模糊C均值聚类后，采空区场地稳定性等级为Ⅰ级(即“稳定路段”)占比36.67%，Ⅱ级(即“基本稳定路段”)占比35.00%，Ⅲ～Ⅳ级(即“欠稳定～不稳定”)的占比为28.33%。对比120个地下开采工作面采空区样本实际稳定性状态，反映在拟建快速路经过该矿路段场地稳定性如图6所示，其中欠稳定路段主要集中在K2+585～K3+373段，降维模糊C均值聚类结果有效性与实际情况相一致，表明该模型具有较满意的聚类效果。
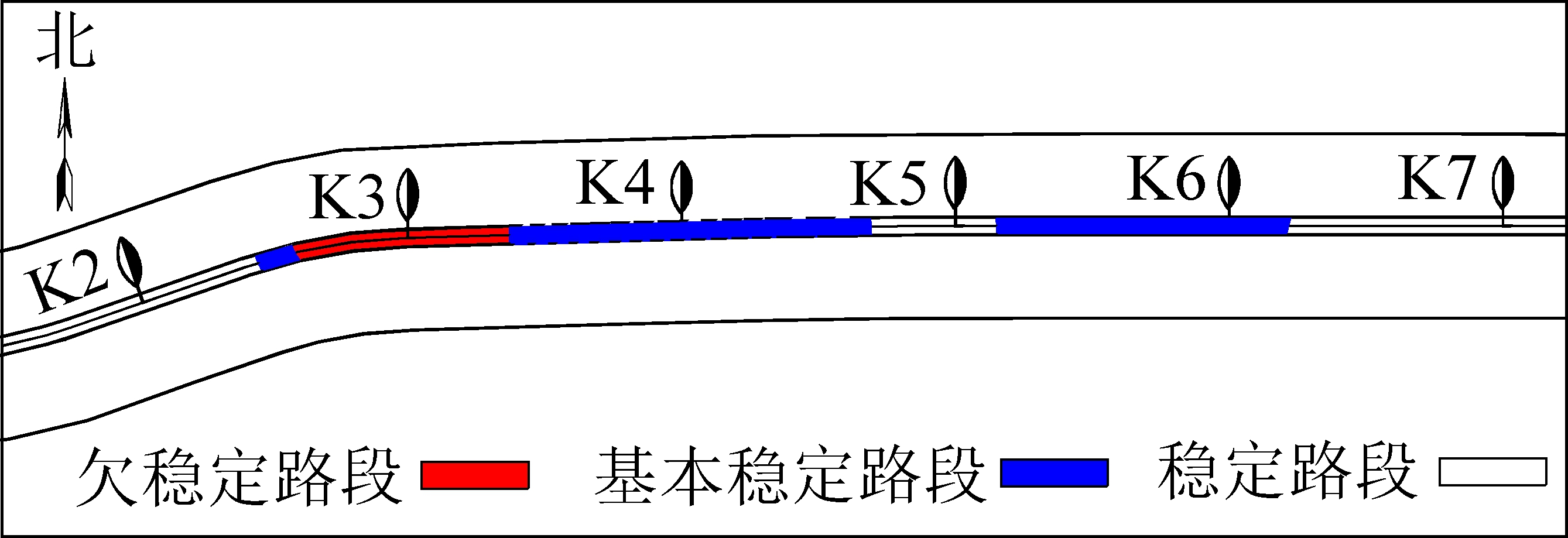
图6 压覆工作面采空区路段场地稳定性示意
Fig.6 Schematic diagram of site stability in goaf section of overburden working face
4 结 论
1)拟建快速路沿线采空区场地稳定及基本稳定路段总长6.06 km，欠稳定路段长0.788 km，降维模糊聚类C均值算法得到的采空区场地稳定性评价结果与定量分析的结果相吻合。算法综合考虑了采厚、采深范围、煤层倾角、工作面走向长度、距离拟建快速路最近距离、停采年限和顶板管理方法等因素，消除了各因素间的相关性，模型构建更严密。
2)主成分分析对影响采空区场地稳定性的高维特征空间数据集进行降维处理，舍弃了3个特征值对应的特征向量，在充分提取有效主成分信息的前提下降低了分类复杂度，最大限度地消除了数据样本之间相关性对分类结果的干扰，在一定程度上起到去噪的效果。
3)降维模糊C均值聚类模型作为迭代更新的“软划分”算法，对于每个样本都有对应的隶属度数组，通过采空区场地稳定性评价结果验证了该方法能够处理非线性多影响因素的大数据样本，可成为解决采空区场地稳定性评价缺少明确判别准则时的有效途径。
参考文献(References):
[1] 童立元,刘松玉,邱 钰,等.高速公路下伏采空区问题国内外研究现状及进展[J].岩石力学与工程学报,2004(7):1198-1202.
TONG Liyuan,LIU Songyu,QIU Yu,et al.Current research state of problems associated with mined-out regions under expressway and future development [J].Chinese Journal of Rock Mechanics and Engineering,2004(7):1198-1202.
[2] LEE Dong，LEE Kil .Assessment of the influencing factors on subsidence at abandoned coal mines in South Korea[J].Environmental Earth Sciences,2013,68(3):647-654.
[3] TONG L,LIAN L,AMATYA B,et al.Risk assessment and remediation strategies for highway construction in abandoned coal mine region:lessons learned from Xuzhou,China[J].Bulletin of Engineering Geology and the Environment,2016,75(3):1-22.
[4] 万战胜,杨 锋,冯振华.采空区建设场地稳定性评价判据探讨[J].西南公路,2016(3):39-44.
WAN Zhansheng,YANG Feng,FENG Zhenhua.Discussion on the evaluation criteria of the construction site stability in goaf [J].Southwest Highway,2016(3):39-44.
[5] 郭庆彪,李英明,王 亮,等.废弃采空区地基稳定性极简评价指标体系构建[J].金属矿山,2019(9):179-184.
GUO Qingbiao,LI Yingming,WANG Liang,et al.Construction of minimalist foundation stability evaluation index system for abandoned goaf [J].Metal Mine,2019(9):179-184.
[6] DIDIER C.Post mining management in France:situation and perspectives[J].Risk Analysis,2010,29(10):1347-1354.
[7] 刘志祥,郭虎强,兰 明.金属矿采空区危险性判别的PCA-SVM模型研究[J].矿冶工程,2014,34(4):16-19.
LIU Zhixiang,GUO Huqiang,LAN Ming.Study on PCA-SVM model for evaluation of gob hazards in metal mine[J].Mining and Metallurgical Engineering,2014,34(4):16-19.
[8] 丁陈建.采动场地残余变形特征及预测模型研究[D].徐州：中国矿业大学,2009.
[9] 李爱兵.基于GIS的金属矿山地质灾害预警系统研究与开发[J].矿业研究与开发,2006，26(S1):131-135.
LI Aibing.Research and development of metal mines geological disaster warning system based on GIS[J].Mining Research and Development,2006，26(S1):131-135.
[10] 葛鹏飞,郭广礼,郭庆彪.基于层次分析法的采空区稳定性评价[J].煤矿安全,2017,48(7):228-231.
GE Pengfei,GUO Guangli,GUO Qingbiao.Stability evaluation of goaf based on analytic hierarchy process[J].Safety in Coal Mines,2017,48(7):228-231.
[11] 郭文兵,刘义新,李小双.采动影响下建筑物损害程度的模糊聚类分析[J].采矿与安全工程学报,2007,24(3):288-292.
GUO Wenbing,LIU Yixin,LI Xiaoshuang.Fuzzy clustering analysis of mining induced damages of buildings[J].Journal of Mining and Safety Engineering,2007,24(3):288-292.
[12] 王正帅,邓喀中.基于核主元分析和模糊聚类的采动区建筑物损害评价[J].煤矿安全,2011,42(4):144-146.
WANG Zhengshuai,DENG Kazhong.Building damage evaluation in mining area based on kernel principal component analysis and fuzzy clustering[J].Safety in Coal Mines,2011,42(4):144-146.
[13] 王正帅,刘冰晶,邓喀中.老采空区稳定性的模糊可拓评价模型[J].地下空间与工程学报,2016,12(2):553-559.
WANG Zhengshuai,LIU Bingjing,DENG Kazhong.Fuzzy extension assessment model of old goaf stability[J].Chinese Journal of Underground Space and Engineering,2016,12(2):553-559.
[14] 宫凤强,鲁金涛.基于主成分分析与距离判别分析法的突水水源识别方法[J].采矿与安全工程学报,2014,31(2):236-242.
GONG Fengqiang,LU Jintao.Recognition method of mine water inrush sources based on the principal element analysis and distance discrimination analysis[J].Journal of Mining and Safety Engineering,2014,31(2):236-242.
[15] 罗东海.模糊评判法在煤矿采空区稳定性评价中的应用[J].水土保持通报,2015(1):176-180，186.
LUO Donghai.Application of fuzzy evaluation method in stability evaluation of mined-out Area[J].Bulletin of Soil and Water Conservation,2015,35(1):176-180，186.
[16] 王心义,姚孟杰,张建国,等.基于改进AHP法与模糊可变集理论的煤层底板突水危险性评价[J].采矿与安全工程学报,2019,36(3):558-565.
WANG Xinyi,YAO Mengjie,ZHANG Jianguo,et.al.Evaluation of water bursting in coal seam floor based on improved AHP and fuzzy variable set theory[J].Journal of Mining and Safety Engineering,2019,36(3):558-565.
[17] 白福均,高建瓴,宋文慧,等.半监督模糊聚类算法的研究与改进[J].通信技术,2018,51(5):1061-1065.
BAI Fujun,GAO Jianling,SONG Wenhui,et al.Exploration and improvement of semi-supervised fuzzy clustering algorithm[J].Communications Technology,2018,51(5):1061-1065.
[18] 彭帅英.高速公路下伏多层采空区地表沉陷数值模拟及预测研究[D].长春：吉林大学,2013.
[19] 王初步,谭富生,王 宇,等.基于数值模拟的复杂采空区稳定性分析[J].矿业研究与开发,2018,38(1):96-100.
WANG Chubu,TAN Fusheng,WANG Yu,et al.Stability analysis on the complicated goaf based on the numerical simulation[J].Mining Research and Development,2018,38(1):96-100.
[20] 杨撷民,霍俊杰,李彦荣.基于MIDAS软件对受采空区影响坡体的稳定性研究[J].煤炭科学技术,2019,47(8):89-95.
YANG Xiemin,HUO Junjie,LI Yanrong.Study on stability of slope affected by goaf based on MIDAS Software[J].Coal Science and Technology,2019,47(8):89-95.
[21] CUI Ximin,ZHAO Yuling,WANG Guorui,et al.Calculation of residual surface subsidence above abandoned longwall coal mining[J].Sustainability,2020,12(4)：1528—1534.
