
移动扫码阅读
王 珍1,曹兰柱2
(1.黄河科技学院 建筑工程学院,河南 郑州 450063;2.辽宁工程技术大学 矿业学院,辽宁 阜新 123000)
摘 要:对数螺旋线破坏机构可充分满足土体速度分离要求,因此对数螺旋线在边坡稳定性上限分析中广泛应用。但由于在平面直角坐标系下对数螺旋线无法显化处理,现阶段上限分析法对均质边坡稳定性分析给出了较好的解答,对于非均质边坡稳定性研究相对较少。为探究上限分析方法在非均质边坡稳定性分析中的应用,基于离散算法提出一种对数螺旋线拟合新方法,并将该方法应用于露天煤矿边坡稳定性上限分析工程实践中,同时基于能量平衡条件编制最危险滑面搜索及稳定系数计算循环程序,并应用剩余推力法从稳定系数与最危险滑面2个角度评价上限分析方法计算结果的准确性。研究结果表明:基于对数螺旋线离散算法计算结果与原曲线具有高度一致性,可保证相关系数大于0.999 5,同时该方法稳定性分析结果具有高度准确性,从稳定系数角度分析该方法计算结果为严格意义上限解,计算误差便于估算,从最危险滑面角度分析,该方法求得的最危险滑面可充分满足速度分离要求,具有更强的工程实践意义。
关键词:对数螺旋线;离散算法;上限分析法;稳定性分析;最危险滑面
中图分类号:TD824.7
文献标志码:A
文章编号:0253-2336(2019)06-0111-06
WANG Zhen1,CAO Lanzhu2
(1.School of Architectural Engineering, Huanghe Science and Technology College, Zhengzhou 450063, China;2.School of Mining, Liaoning Technical University, Fuxin 123000, China)
Abstract:The logarithmic spiral damage mechanism can fully meet requirements of soil velocity separation, so the logarithmic spiral is widely used in the upper limit analysis of slope stability.However, since the logarithmic spiral can′t be manifested in Cartesian Coordinate System, the current upper bound analysis method gives a perfect solution to the homogeneous slopes stability analysis although the research of heterogeneous slope stability is relatively rare.In order to disscus the application of upper limit analysis method in heterogeneous slope stability,the authors proposed a new method of logarithmic spiral fitting based on discrete algorithm, and applied this method to the engineering practice of upper limit analysis of slope stability in open-pit mine.At the same time, the most dangerous slip surface and the slope stability coefficient calculation cycle program was compiled based on energy balance condition, and the residual thrust method was used to evaluate accuracy of calculation result of upper limit analysis method from two angles of stability coefficient and the most dangerous slip surface.The results show that the logarithmic spiral discrete algorithm is highly consistent with the original curve, which can guarantee the requirement R2≥0.999 5.At the same time, the stability analysis results are highly accurate.The calculation result is analyzed from perspective of stability coefficient.From the perspective of stability factors, the calculation result is strictly the upper bound solution, and the calculation error is easy to estimate.From the perspective of the most dangerous slip surface,the most dangerous slip surface obtained by this method can fully satisfy the requirements of speed separation and has a stronger engineering practice significance.
Key words:logarithmic spiral;discrete algorithm; upper limit analysis; stability analysis; the most dangerous slip surface
王 珍,曹兰柱.基于对数螺旋线离散算法的露天煤矿边坡稳定性研究[J].煤炭科学技术,2019,47(6):111-116.doi:10.13199/j.cnki.cst.2019.06.017
WANG Zhen,CAO Lanzhu.Study on slope stability of surface coal mine based on logarithmic spiral discrete algorithm[J].Coal Science and Technology,2019,47(6):111-116.doi:10.13199/j.cnki.cst.2019.06.017
收稿日期:2019-03-01
责任编辑:曾康生
基金项目:高等学校博士学科点专项基金资助项目(NO.20122121110003),辽宁省煤炭资源安全开采与洁净利用工程研究中心开放基金资助项目(NO.LNTU15KF08)
作者简介:王 珍(1989—),女,河南郑州人,博士,讲师。E-mail:15841836133@163.com
通用作者:曹兰柱(1962—),男,内蒙古四王子旗人,教授,博士生导师。
在极坐标系下,对于通过旋转中心的任意直线,其与对数螺旋线的交角始终相等,因此对数螺旋线又被称之为等角螺旋线[1]。由于这种良好的几何、数学特性,对数螺旋线在机械工程、天文气象、岩土工程等诸多领域应用广泛。其中岩土工程中关联流动法则要求相对速度变化方向与滑裂面切向方向夹角为内摩擦角[2-3]。这种速度分离要求与对数螺旋线几何特性具有高度一致性,因此,对数螺旋线在岩土工程领域应用最为广泛。
1951年著名学者DRUCKER[4]以稳定材料为前提,提出屈服准则相关联的流动法则,使传统塑性位势理论产生新突破。随后,学者DRUCKER[5]将静力许可应力场以及运动许可的速度场联立,建立了极限分析理论,并将该理论应用于极限荷载值求解的问题中,取得了良好的计算效果。1975年,学者CHEN[6]将极限分析理论中上限分析法引入岩土体结构分析中,并发表专著详细说明上限分析法在岩土体机构中应用原理及计算流程。此后数十年间,上限分析法成为岩土工程领域重点课题,广大学者将其应用于地下空间工程[7]、边坡与基坑工程[8]、地基承载力计算[9]、围岩塌落及稳定分析[10]等诸多领域,并取得了显著的成果。现阶段,上限分析法得到了广大学者高度认可,基于上限分析法可知,岩土体破坏迹线形态并非以圆弧为界限,而是以对数螺旋线为界。正是由于这种特殊的性质,上限分析法在均质岩土体结构分析中应用广泛,而在非均质岩土体结构分析中受到了极大限制。王根龙等[11]基于ANSYS有限元前处理功能,对非均质边坡稳定性进行上限分析研究,并给出了非均质边坡极限分析法稳定系数计算式。孙志斌等[12]应用极限分析有限元技术,对非均质边坡的二维稳定性进行分析计算,并实现了最危险滑面的搜索。虽然有限元技术可解决上限分析法在非均质岩土体结构分析中存在的困难,但由于有限元技术搜索过程复杂,计算过程繁琐,导致分析效果并不理想。
为简化上限分析法在非均质岩土体结构分析中的应用,本文结合离散算法提出对数螺旋线拟合新方法,并将该方法应用于露天矿山边坡稳定性上限分析中,编制最危险滑面搜索及稳定系数计算循环程序,从数学角度解决上限分析法在非均质边坡稳定性分析中的应用,对分析结果做出准确性评价。该方法可充分简化计算过程,提高运算速率,具有重要的理论意义及推广价值。
对数螺旋线方程在平面直角坐标系下函数表达式复杂,为工程实践应用带来巨大挑战。因此采用离散算法进行对数螺旋线拟合,在极坐标系下,对数螺旋线方程可表示为
r=aeθtan φ
(1)
式中:r为旋转中心与对数螺旋线距离;a为对数螺旋线待定参数;θ为旋转中心与对数螺旋线连线的水平夹角;φ为通过旋转中心的直线与对数螺旋线的夹角。
以极坐标系中旋转中心为坐标原点,水平方向为X轴,竖直方向为Y轴,建立平面直角坐标系。根据极坐标系与平面直角坐标系二者间的坐标转换关系,对数螺旋线在平面直角坐标系下的横纵坐标(x,y)可分别表示为
(2)
(3)
在岩土工程领域一般认为φ可取岩体的内摩擦角,该参数可通过力学试验测得。式(2)和式(3)表明:x/a与y/a均是只关于参数θ的隐函数,但该隐函数显化存在极大困难。显然,对数螺旋线是由无限点构成的平面曲线,工程实践中通常选取第四象限增区间进行计算。因此将对数螺旋线第四象限增区间内的函数曲线在Y方向上进行有限等分,通过各等分点平面直角坐标值进行最小二乘拟合,最终确定平面直角坐标系下对数螺旋线的拟合函数表达式。下文中以φ=45°为例说明该拟合过程。
当φ=45°时,tan φ=1,则对数螺旋线方程可表示为r=aeθ。以水平方向为x轴,竖直方向为y轴建立平面直角坐标系,在平面直角坐标系下,对数螺旋线横坐标可表示为x=aeθcos θ,纵坐标可表示为y=-aeθsin θ。以y为自变量,x为因变量建立函数关系,应用数学分析软件可求得该函数在第四象限内的增区间为y∈(-4.811a,-1.551a)。之后在增区间范围内以0.001a为有效步长进行离散化处理,并计算各离散点平面直角坐标值,最后通过最小二乘法对各离散点坐标值进行多项式拟合,并分析拟合相关性,该拟合结果见表1。
由表1可知,当采用四次多项式拟合时,对数螺旋线拟合结果相关性系数R2=0.999 8,可充分满足R2≥0.999 5,拟合效果良好,可充分满足工程计算的需求。
表1 对数螺旋线拟合结果
Table 1 Logarithmic spiral fitting result

某露天矿山北帮为非工作帮,边坡坡面角α=28°,边坡岩层由表土、泥岩构成。表土容重γ1=18.5 kN/m3,黏聚力c1=40 kPa,内摩擦角φ1=10°,岩层厚度h1=25 m。泥岩容重γ2=21 kN/m-3,黏聚力c2=90 kPa,内摩擦角φ2=22°,岩层厚度h2=45 m。该矿山边坡工程经验表明,北帮边坡易发生起始于边坡坡顶并通过坡趾的剪切破坏。根据岩层力学性质差异以及关联流动法则要求,矿山北帮边坡破坏机构可近似由两条对数螺旋线组合而成,矿山北帮边坡破坏机构形态如图1所示。
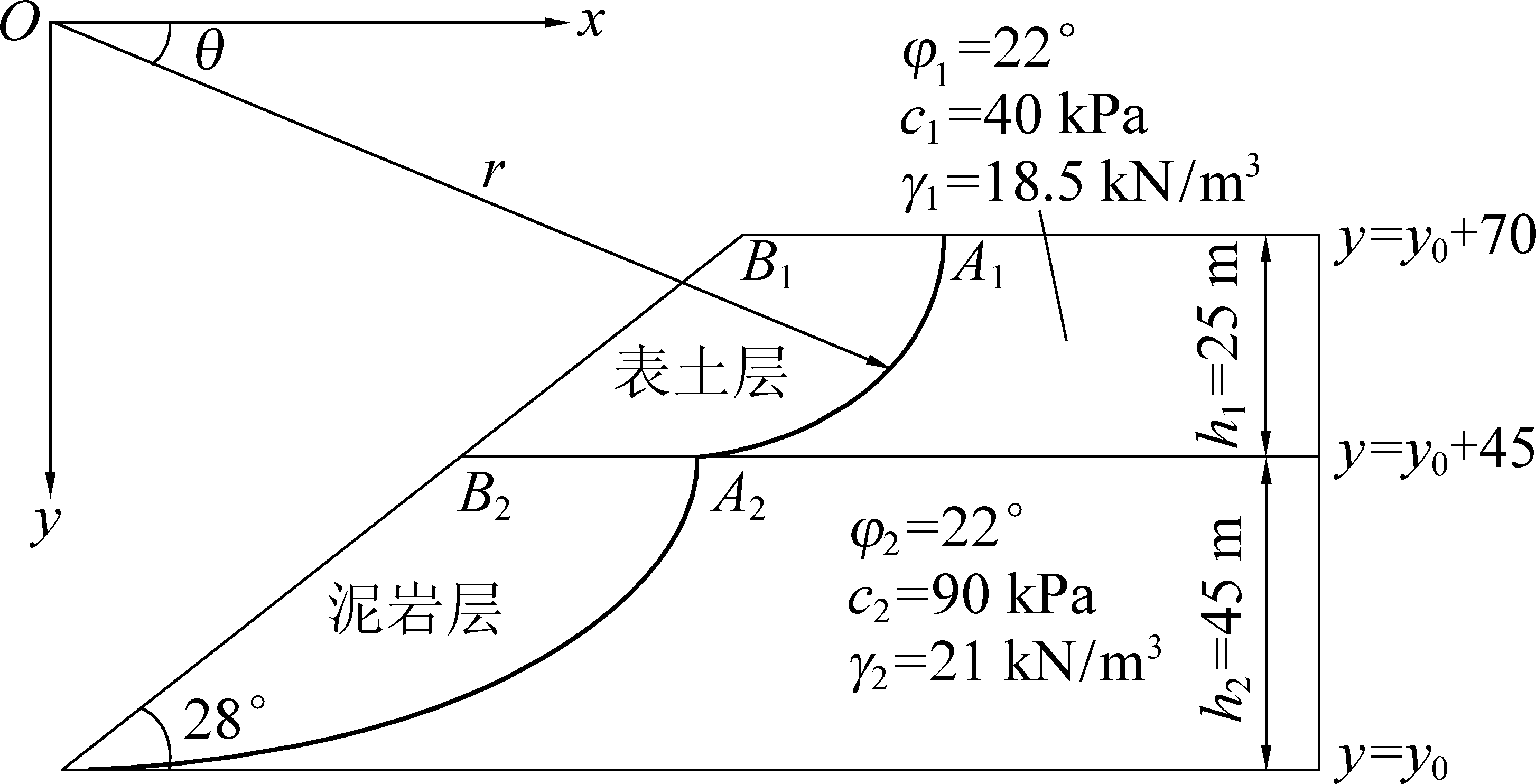
图1 北帮破坏机构示意
Fig.1 Failure mechanism illustration of north slope
水平方向为X轴,竖直方向为Y轴建立平面直角坐标系,令图1中泥岩底板方程为y=y0,根据泥岩厚度为45 m,则泥岩顶板(表土底板)方程可表示为y=y0+45,同理,表土顶板(地表)方程可表示为y=y0+70。边坡坡面角α=28°,因此边坡坡面方程可表示为g(y)=1.880 7y+b。同时,由于表土内摩擦角φ1=10°,泥岩内摩擦角φ2=22°,可确定表土、泥岩两岩层内破坏机构极坐标方程可表示为
r1=a1eθtanφ1=a1e0.176θ
(4)
r2=a2eθtanφ2=a2e0.404θ
(5)
式(4)为表土内破坏机构极坐标方程,该方程第四象限增区间为[-1.318 5a1,-0.178 5a1],式(5)为泥岩内破坏机构极坐标方程,该方程第四象限增区间为[-1.886 3 a2,-0.437 5a2]。应用上节中对数螺旋线拟合方法对表土、泥岩这2种岩层破坏机理进行多项式拟合,要求多项式拟合结果相关系数R2≥0.999 5,则多项式拟合结果可表示为
f1(y)=0.851 1a1-1.450 5y-4.091 2y2/a1-4.128 1×
(6)
f2(y)=0.832 4a2-1.191 5y-1.856 6y2/a2-1.084 6×
(7)
式(6)、式(7)分别为表土、泥岩内破坏机构多项式拟合结果,该拟合结果可充分满足相关性系数R2≥0.999 5的要求。则边坡岩层顶底板、边坡坡面以及边坡破坏机构在平面直角坐标系下函数表达式均已知,边坡计算模型建立完毕。
上限分析法基于塑性力学基本原理,从能量与速度的角度分析边坡稳定性。由于能量属于标量,可有效避免映射方法不一致导致的稳定系数不统一。上限分析法核心为对于任意一个有效的破坏机构,令外力功率等于内能耗散率,便可得到破坏载荷或极限载荷的不安全上限[13-14],基于此可进行边坡稳定性分析。
2.3.1 边坡外力功率计算
自然状态下边坡岩土体外力功率全部由重力功率提供。边坡发生剪切破坏时,根据线速度与角速度关系,在重力方向上的分速度可表示为
v=ωrcos θ=ωx
(8)
式中:v为岩体重力方向分速度,m/s;w为岩体角速度,rad/s。
根据破坏机构形态及边坡计算模型,表土和泥岩两层岩内破坏区域可分别表示为
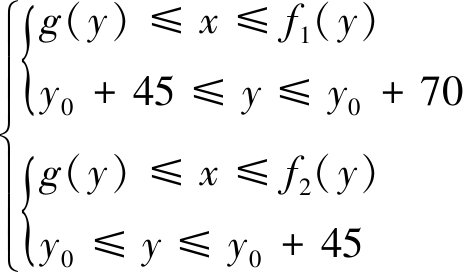
(9)
根据重力方向上分速度表达式及岩层破坏区域表达式,可确定本矿山边坡外力功率表达式为
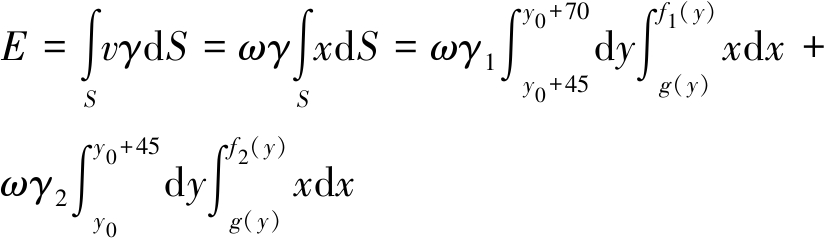
(10)
2.3.2 边坡内能耗散率计算
上限分析法假定滑体为完全刚性块体,滑裂面为速度间断面。根据塑性力学基本理论,滑裂面上摩擦能耗与假想存在的剪胀能耗恰好可完全抵消,因此内能耗散全部由黏聚力提供,且全部集中于速度间断面(滑裂面)上。
选取表土岩层内对数螺旋线上的微元长度为rdθ/cos φ1,该微元对应的黏聚力为c1rdθ/cos φ1。因此表土内滑裂面方向上内能耗散率可表示为
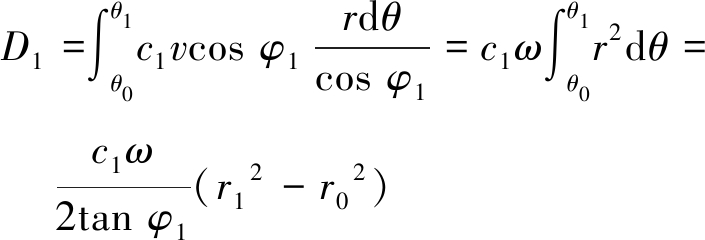
(11)
其中:θ0、θ1分别为旋转中心与表土岩层对数螺旋线起点、终点连线水平方向夹角,rad;r0、r1分别为旋转中心与表土岩层对数螺旋线起点、终点的距离,m。根据两点间距离式,表土岩层内滑裂面方向上内能耗散率D1,可表示为
![]()
![]()
(12)
同理,泥岩岩层内对数螺旋线上内能耗散率D2可表示为
(13)
该边坡内能耗散率D可通过表土、泥岩2层岩体内能耗散率相加求得,即D=D1+D2。
2.3.3 强度折减计算
根据该矿山边坡破坏规律,以及坐标点的唯一性,可确定约束条件为
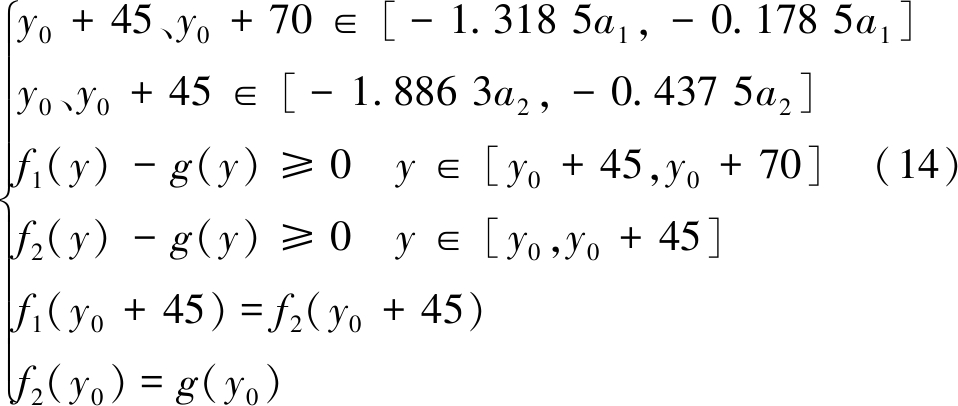
根据外力功率及内能耗散率计算式及边坡约束条件,应用数学分析软件可计算未进行强度折减时内能耗散率与外力功率比值最小值,比值最小值ε=10.236,边坡处于非平衡状态。为使边坡由非平衡状态逐步过渡至极限平衡状态,笔者应用强度折减法对边坡强度指标进行折减,其折减方程式为
(15)
式中:![]() 为强度折减后岩体黏聚力;
为强度折减后岩体黏聚力;![]() 为强度折减后岩体内摩擦角;F为强度折减系数。
为强度折减后岩体内摩擦角;F为强度折减系数。
强度折减过程中,由于需对内摩擦角进行强度折减,会影响对数螺旋线拟合结果。因此人工计算折减至极限平衡状态较为复杂,应借助计算机循环功能实现强度折减。
2.3.4 循环计算流程
由稳定系数定义可知,强度折减系数F等于边坡稳定系数Fs时,内能耗散率与外力功率比值最小值ε=1。同时二者比值最小值ε与强度折减系数F呈现严格单调递减关系。基于以上这2个方面特征,可以构建函数ε=(D/E)min。显然,ε-1在正实数范围内有且只有一个零点,因此采用二分法编制最危险滑面搜索及稳定系数计算循环程序,将∣ε-1∣≤0.001近似为函数ε-1零点,并作为程序终止条件,循环计算流程如图2所示。
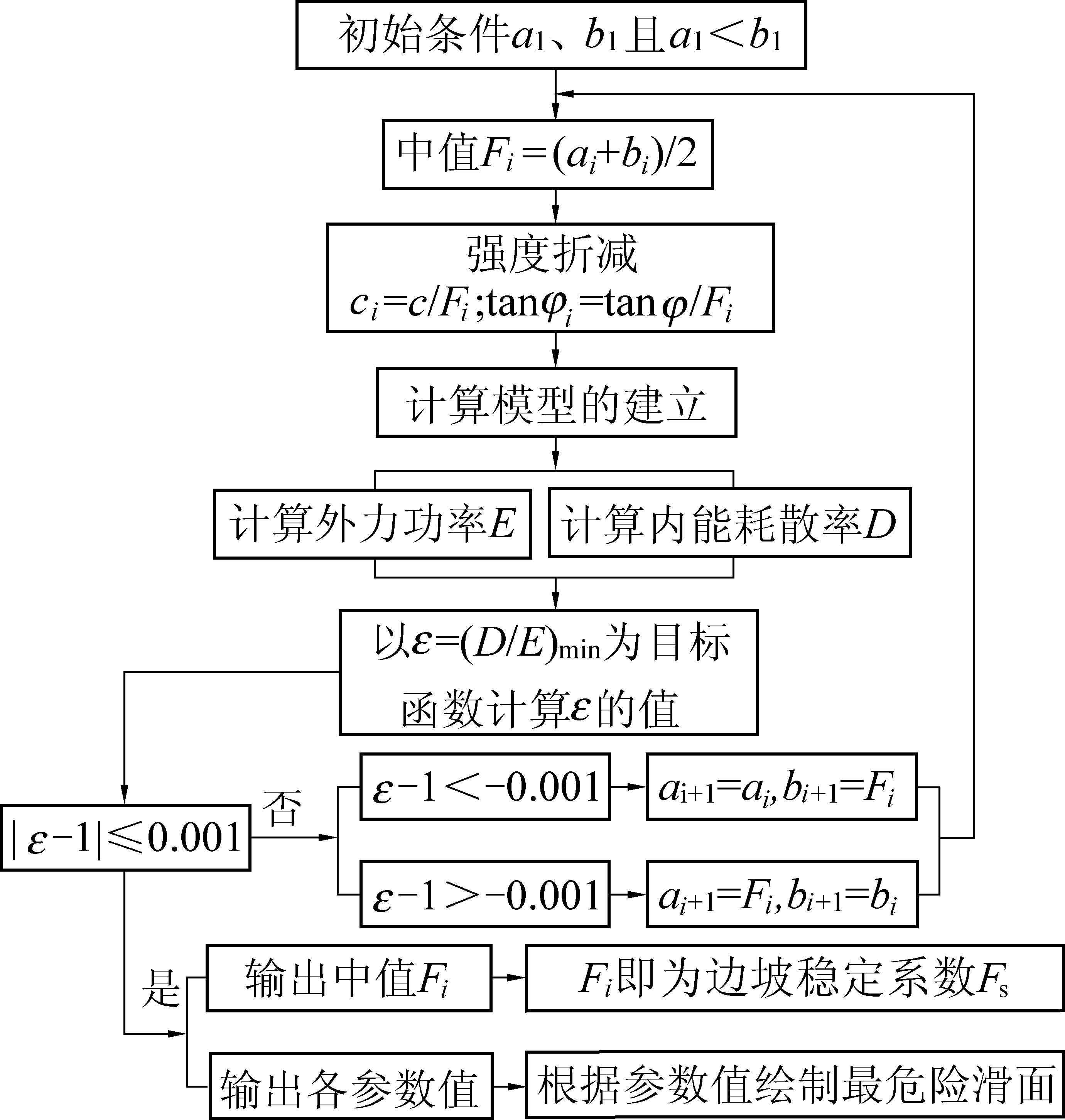
图2 计算流程
Fig.2 Calculation process
图2计算流程中,初始值a1、b1所构成的区间应严格包含任意形态边坡稳定系数。本文选取初始值a1=0,b1=4作为循环初始条件。通过图2计算流程可最终输出满足∣ε-1∣≤0.001的强度折减系数F,根据前文中的假设条件,该强度折减系数F即可近似为边坡稳定系数Fs。同时,根据内能耗散率与外力功率二者比值取得最小值时所对应的各参数值可绘制边坡滑裂面形态,该滑裂面即边坡的最危险滑面。
2.3.5 循环计算结果
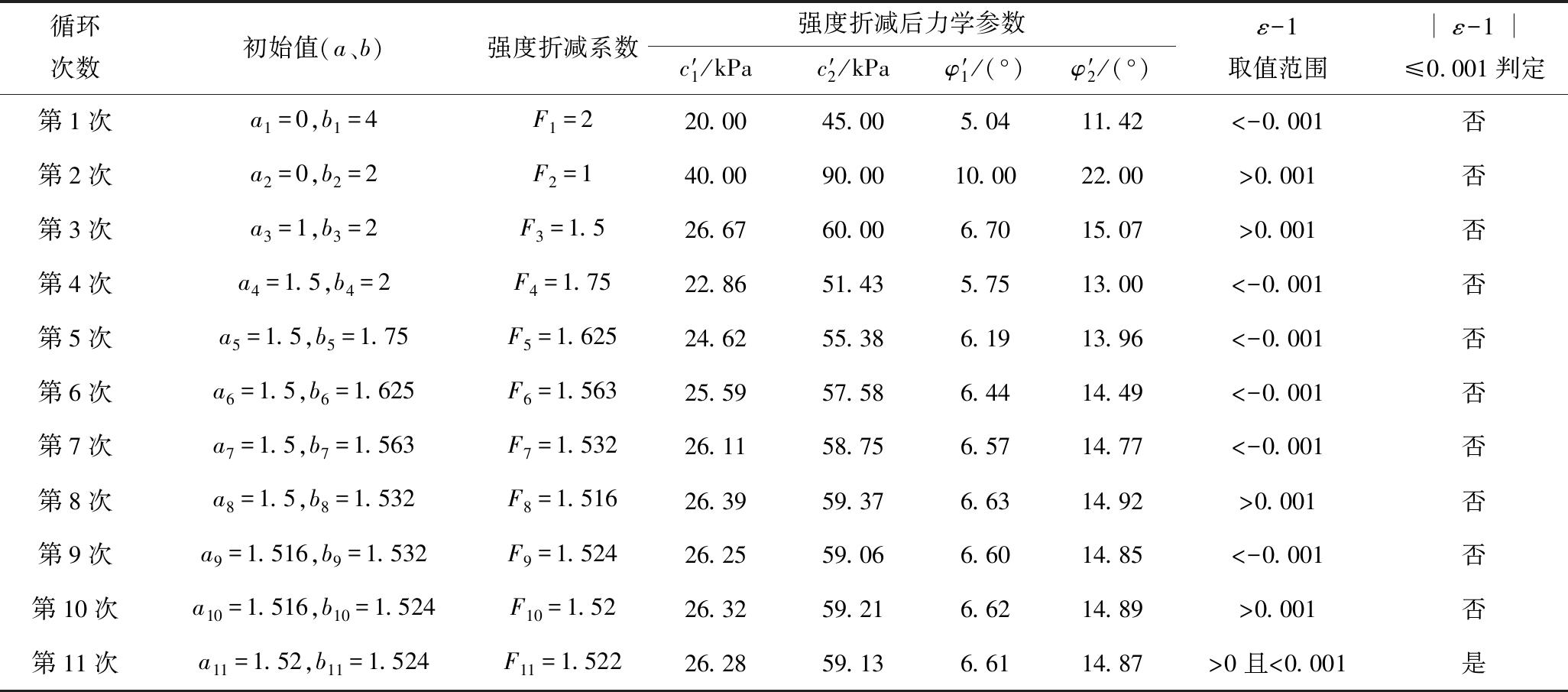
选取初始值a1=0,b1=4进行强度折减循环计算,最终输出满足∣ε-1∣≤0.001的强度折减系数F,该循环程序计算流程及结果见表2。
计算结果表明:循环次数达到11次时,输出结果满足∣ε-1∣≤0.001的要求,此时强度折减系数F11=1.522,因此该边坡稳定系数Fs=1.522。同时,根据内能耗散率与外力功率比值取得最小值时对应的参数值可绘制边坡最危险滑面形态,该边坡稳定性上限分析法计算结果如图3所示。
表2 强度折减循环计算结果
Table 2 Cycle calculation results of strength reduction
上限分析法从功能平衡的角度进行稳定性分析,而极限平衡法从静力平衡与力矩平衡的角度进行稳定性分析,2种方法分析角度截然不同,但计算结果应具备高度一致性[15-16]。笔者选取极限平衡法中的剩余推力法进行计算结果评价,剩余推力法边坡稳定性计算结果如图3所示。
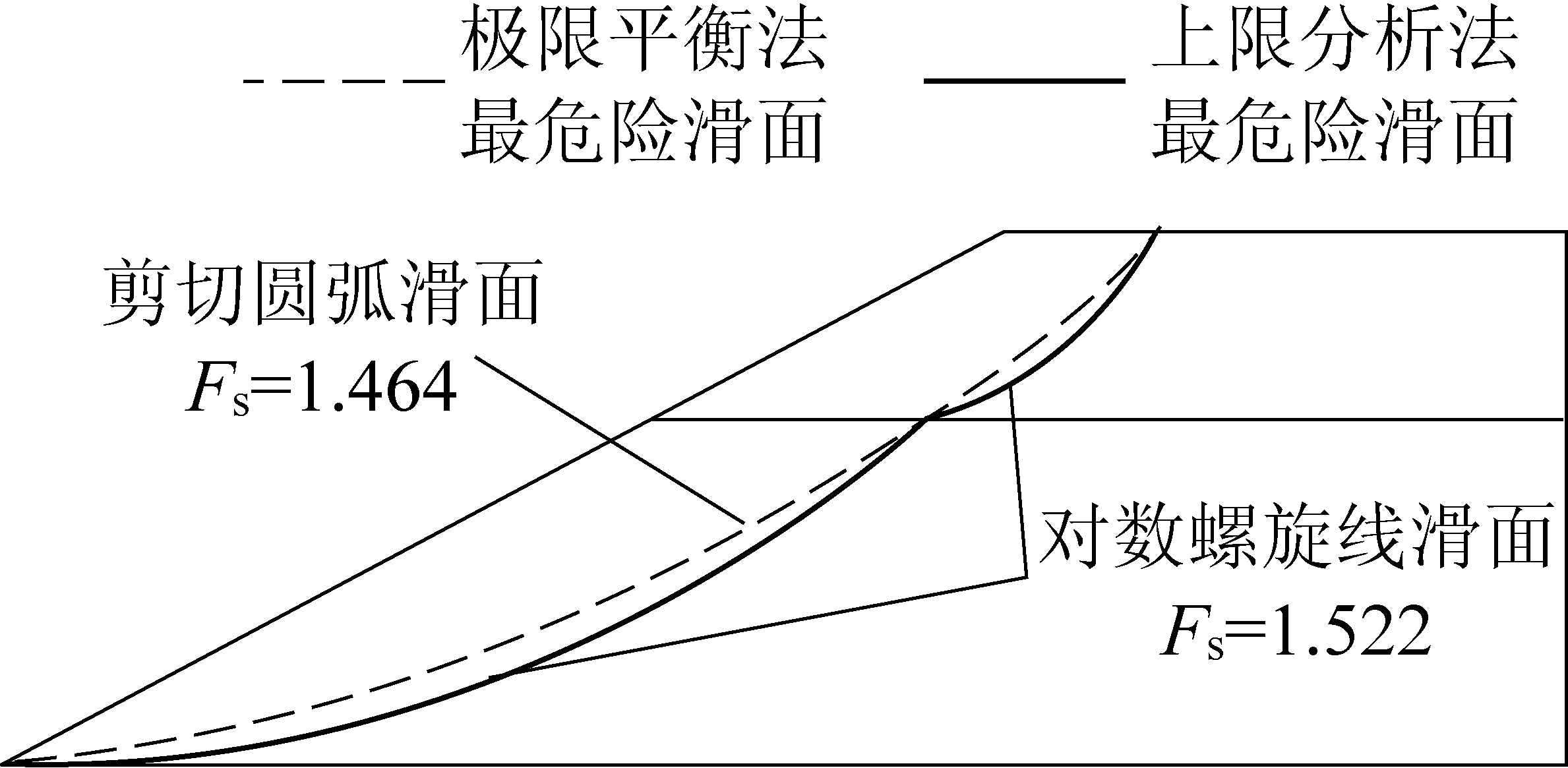
图3 边坡稳定性计算结果
Fig.3 Calculation results of slope stability
从稳定系数角度分析,剩余推力法假设条块对下一条块的推力方向平行于底滑面。当滑体底滑面较陡时,分界面剪应力可能超过边坡抗剪强度,导致计算结果偏危险;反之当滑体底滑面较缓时,分界面虽满足边坡合理性条件,但可能导致计算结果偏保守[17-19]。因此剩余推力法稳定系数计算结果虽具备一定准确率,但计算误差难于估算。而上限分析法构建静力许可的应力场和运动许可的速度场来寻求边坡变形破坏机制,求得泛函值为上限荷载值,因此稳定系数计算结果为严格意义上限解,误差易于估算。这2种方法稳定系数计算结果误差率小于5%,充分满足工程实践需要,验证了计算结果的准确性。
从最危险滑面角度进行分析,两方法最危险滑面的起始点与终止点完全一致,滑面形态也基本相同,但剩余推力法最危险滑面形态为剪切圆弧滑面,而上限分析法最危险滑面形态为组合对数螺旋线滑面[20]。根据塑性力学中关联流动法则规定,相对速度变化方向与滑裂面方向夹角为内摩擦角φ,而上限分析法最危险滑面可充分满足该要求,因此上限分析法求得的最危险滑面具有更强的工程参考意义。
1)采用离散算法提出一种简洁、准确的对数螺旋线拟合方法,并通过相关性分析验证了对数螺旋线离散算法与原曲线具备高度一致性,相关系数R2≥0.999 5,可充分满足工程实践需求。
2)将本文提出的拟合方法应用至露天矿山边坡稳定性上限分析工程实践中,并基于能量平衡条件编制最危险滑面搜索及稳定系数计算循环程序。
3)应用剩余推力法对工程实践中稳定性分析结果进行评价,验证了该方法稳定性分析结果具备高度的准确性。
4)工程实践分析结果表明,相比于剩余推力法,上限分析法稳定系数计算结果为严格意义的上限解,计算误差便于估算;同时上限分析法求得的最危险滑面可满足土体速度分离要求,因此具有更强工程实践意义。
参考文献(References):
[1] 杨 敏,种劲松.基于对数螺旋线边缘拟合的SAR图像漩涡信息提取方法[J].雷达学报,2013,2(2):226-233.
YANG Min,ZHONG Jinsong.A method based on logarithmic spiral edge fitting for information extraction of eddy in the SAR image[J].Journal of Radars,2013,2 (2):226-233.
[2] 郑颖人,孔 亮.广义塑性力学及其运用[J].中国工程科学,2005,7(11):25-40.
ZHENG Yingren,KONG Liang.Generalized plastic mechanics and its application[J].Engineering Science,2005,7(11):25-40.
[3] 郑颖人,赵尚毅.有限元强度折减法在土坡与岩坡中的应用[J].岩石力学与工程学报,2004,23(19):3381-3388.
ZHENG Yingren,ZHAO Shangyi.Application of strength reduction FEM in soil and rock slope[J].Chinese Journal of Rock Mechanics and Engineering,2004,23(19):3381-3388.
[4] DRUCKER D C,GREENBERG H J,PRAGER W.The safety factor of an elastic-plastic body in plane strain[J].Journal of Applied Mechanics Transactions of the ASME,1951,18 (4):371-378.
[5] DRUCKER D C,PRAGER W,GREENBERG H J.Extended limit design theorems for continuous media[J].Quarterly of Applied Mathematics,1952,9(4):381-389.
[6] CHEN W F.Limit analysis and soil plasticity[M].New York:Elsevier Scientific Publishing Co,1975.
[7] 聂卫平,徐卫亚,王 伟,等.大型地下洞室极限位移预测与稳定性分析[J].岩石力学与工程学报,2012,31(9):1901-1907.
NIE Weiping,XU Weiya,WANG Wei,et al.Limit displacement prediction and stability analysis of large underground caverns[J].Chinese Journal of Rock Mechanics and Engineering,2012,31(9):1901-1907.
[8] YANG X L,YIN J H.Slope stability analysis with nonlinear failure criterion[J].Journal of Engineering Mechanics,2004,130(3):267-273.
[9] 胡卫东,曹文贵.基于非对称破坏模式的临坡地基承载力上限极限分析方法[J].中国公路学报,2014,27 (6):1-9.
HU Weidong,CAO Wengui.Upper limit limit analysis method for ultimate bearing capacity of ground foundation adjacent to slope based on asymmetry failure mode[J].China Journal of Highways and Transport,2014,27(6):1-9.
[10] YANG X L.Upper bound limit analysis of active earth pressure with different fracture surface and nonlinear yield criterion[J].Theoretical and Applied Fracture Mechanics,2007,47(1):46-56.
[11] 王根龙,伍法权,张军慧.非均质土坡稳定性分析评价的刚体单元上限法[J].岩石力学与工程学报,2008,27(S2):3425-3430.
WANG Genlong,WU Faquan,ZHANG Junhui.Upper bound approach of rigid elements for inhomogeneous soil slope stability analysis[J].Chinese Journal of Rock Mechanics and Engineering,2008,27(S2):3425-3430.
[12] 孙志彬,潘秋景,杨小礼,等.非均质边坡上限分析的离散机构及应用[J].岩石力学与工程学报,2017,36 (7):1680-1688.
SUN Zhibin,PAN Qiujing,YANG Xiaoli,et al.Discrete mechanism for upper bound analysis of non-homogeneous slopes[J].Chinese Journal of Rock Mechanics and Engineering,2017,36 (7):1680-1688.
[13] 陈祖煜.土力学经典问题的塑性力学上、下限解[J].岩土工程学报,2002,24(1):1-11.
CHEN Zuyu.Limit analysis for the classic problems of soil mechanics[J].Chinese Journal of Geotechnical Engineering,2002,24(1):1-11.
[14] 王 珍,曹兰柱,王 东.非均质边坡稳定性上限分析评价研究[J].岩土力学,2019,40(2):737-742.
WANG Zhen,CAO Lanzhu,WANG Dong.Evaluation on upper limit of heterogeneous slope stability[J].Rock and Soil Mechanics,2019,40(2):737-742.
[15] 曹兰柱,李广贺,王 东,等.露天矿顺倾软弱基底内排土场边坡空间形态优化[J].煤炭科学技术,2018,46(2):163-167.
CAO Lanzhu,LI Guanghe,WANG Dong,et al.Optimization on spatial morphology slope of in pit dumping site at inclined weak-basement of surface mine[J].Coal Science and Technology,2018,46(2):163-167.
[16] 王 东,王 珍,曹兰柱,等.近水平煤层露天矿边坡三维稳定性研究[J].煤炭科学技术,2016,44(8):86-90.
WANG Dong,WANG Zhen,CAO Lanzhu,et al.Study on 3D stability of slope in surface mine with sub-horizontal seams[J].Coal Science and Technology,2016,44(8):86-90.
[17] 张宜虎,尹红梅,简文星.剩余推力法及其在斜坡稳定性评价中的应用[J].岩土力学,2004,25(4):628-631.
ZHANG Yihu,YIN Hongmei,JIAN Wenxing.The remained slip force method considering the effect of rainfall and its application to assessment of slope stability [J].Rock and Soil Mechanics,2004,25(4):628-631.
[18] 曹兰柱,王 珍,王 东,等.露天煤矿端帮逆倾软岩边坡稳定性研究[J].煤炭科学技术,2017,45(3):1-6.
CAO Lanzhu,WANG Zhen,WANG Dong,et al.Study on stability of reversed inclined soft rock slope at end slope of surface mine[J].Coal Science and Technology,2017,45(3):1-6.
[19] 徐 青,陈士军,陈胜宏.滑坡稳定分析剩余推力法的改进研究[J].岩土力学,2005,37(3):465-470.
XU Qing,CHEN Shijun,CHEN Shenghong.Study on the improved residual threst method for landslide stability analysis[J].Rock and Soil Mechanics,2005,37(3):465-470.
[20] 张小艳,张立翔,李 泽.基于塑性极限分析上限法理论的土质边坡可靠度分析[J].岩土力学,2018,39(5):1840-1850.
ZHANG Xiaoyan,ZHANG Lixiang,LI Ze.Reliability analysis of soil slope based on upper bound method of limit analysis[J].Rock and Soil Mechanics,2018,39(5):1840-1850.