
移动扫码阅读
安全技术及工程
矿井火灾是煤矿重大灾害之一[1-3],巷道一旦发生火灾,火势发展迅速、变化复杂、影响范围广[4-5],对井下工作人员及设备构成严重危害。矿井火灾会引发瓦斯爆炸,其危害性居各种重大、恶性和突发性事故之首[6-7]。而入口风速的大小直接影响巷道内的风流状态,准确掌握火灾引起的风流紊乱对瓦斯涌出浓度的影响,对防止瓦斯超限引起的爆炸有重大意义。
随着科学技术的发展和计算机技术在流体力学领域的应用,计算机模拟已成为研究和分析流体流动问题的有效方法[8],对减少火灾时期人员伤亡、控制火势蔓延等有重大意义[9-10]。国内外学者在相关领域都做了大量研究工作。最早进行该方面研究的是澳大利亚的格林A R和尤普福尔德R W,建立了基于燃烧学的瓦斯和煤尘爆炸传播过程的计算机数值计算模型[11]。马洪亮等[12]对矿井火灾进行了模拟,火源采用的是固定输出热量的稳定火源,这种方法对于不考虑发展过程的火灾对巷道风流的影响问题有重要的借鉴作用。周西华等[13]对风流在巷道中的流动进行了二维模拟,反映出其所在平面的分布情况。文献[9-10,14]用 Fluent 软件对巷道火灾时期进行数值模拟计算,对速度场、温度场进行分析,得出了速度变化规律及烟流在火源一定条件下发生倒流的结论。
前人对火灾时期巷道内烟流分布规律的研究很多,但是很少对比研究不同入口风速对巷道内流场的影响以及火灾后的瓦斯含量是否会引发爆炸。笔者在前人研究的基础上,模拟不同风速条件下发生火灾时风流在巷道的流动情况,还具体考虑火源上方风流的速度场、温度场、瓦斯及CO浓度场,对实际巷道火灾后的影响及判断是否会产生瓦斯超限引发爆炸有重要的借鉴意义。
在火灾模拟计算中采取了一定的假设[15]:将烟气视为理想气体,满足理想气体状态方程;假定沿程的巷道壁面粗糙程度相同,巷道壁面绝热,与风流气体没有热交换,壁面速度为0;巷道风流可视为不可压缩流体,黏性的影响忽略不计,流动为稳态湍流,满足Boussinesq假设,空气密度为常数;巷道内无相关工作人员、杂物堆放、运输车辆和相关设备等障碍物[16]。
根据上述假设,笔者采用有限体积方法进行模拟[17],控制方程有连续性方程、动量守恒方程、能量守恒方程、湍流方程、组分质量守恒方程。其中,组分为甲烷-空气的混合组分。
1)质量守恒方程为
(1)
式中:ρ为流体的密度;t为时间;vi为i方向的速度;xi为i方向位置分量。
2)动量守恒方程为
(2)
(3)
式中:P为静压力;ui、uj为速度矢量分别在i、j方向上的分量;xj为j方向位置分量。τij为应力张量值;gi为i方向的重力加速度;Fi为由热源、污染源等引起的源项;μ为分子的黏度系数。δij为Kronecker delta符号(当i=j时,δij=1;当i≠j时,δij=0)。
3)能量守恒方程为
(4)
式中:cp比热容;T为温度;K为流体的传热系数;ST为黏性耗散项。
4)湍流方程。
由于该模型假设流动为完全湍流且分子黏性的影响忽略不计,因此笔者采用湍流标准k-ε计算模型。
k方程为
(5)
ε方程为
(6)
式中:k为湍流动能;μeff为耗散黏度;Gk为湍流动能,由层流速度梯度产生;ε为湍流动能耗散率;YM为由于扩散而产生的波动;αk、αε为k、ε的湍流普朗特数的倒数;C1、C2为经验常数。
5)组分质量守恒方程为
(7)
式中:m为组分的质量;cz为流体中组分z的体积分数;Dz为组分z在流体中的扩散系数;Sz为单位时间单位体积组分的生成量。
根据煤矿工作面实际巷道尺寸建立三维数值分析模型。巷道截面为矩形截面,截面尺寸为:宽3.8 m、高3.1 m,截面面积为11.78 m2,巷道长度为90 m;根据流体力学中水力直径的计算公式可计算出矩形截面的水力直径D=3.414 m[18]。
模型的三维直角坐标系以巷道的长为X轴方向,巷道断面的宽为Z轴方向,以断面的高为Y轴方向。
将中下部的长方体设为火源点,用于热量辐射,其尺寸为2 m×1 m×1 m。为尽可能具体地反应巷道内灾变时期风流流动规律,火源设定为2 000 K的高温热源。简化后的几何模型如图1所示,横纵截面如图2所示。
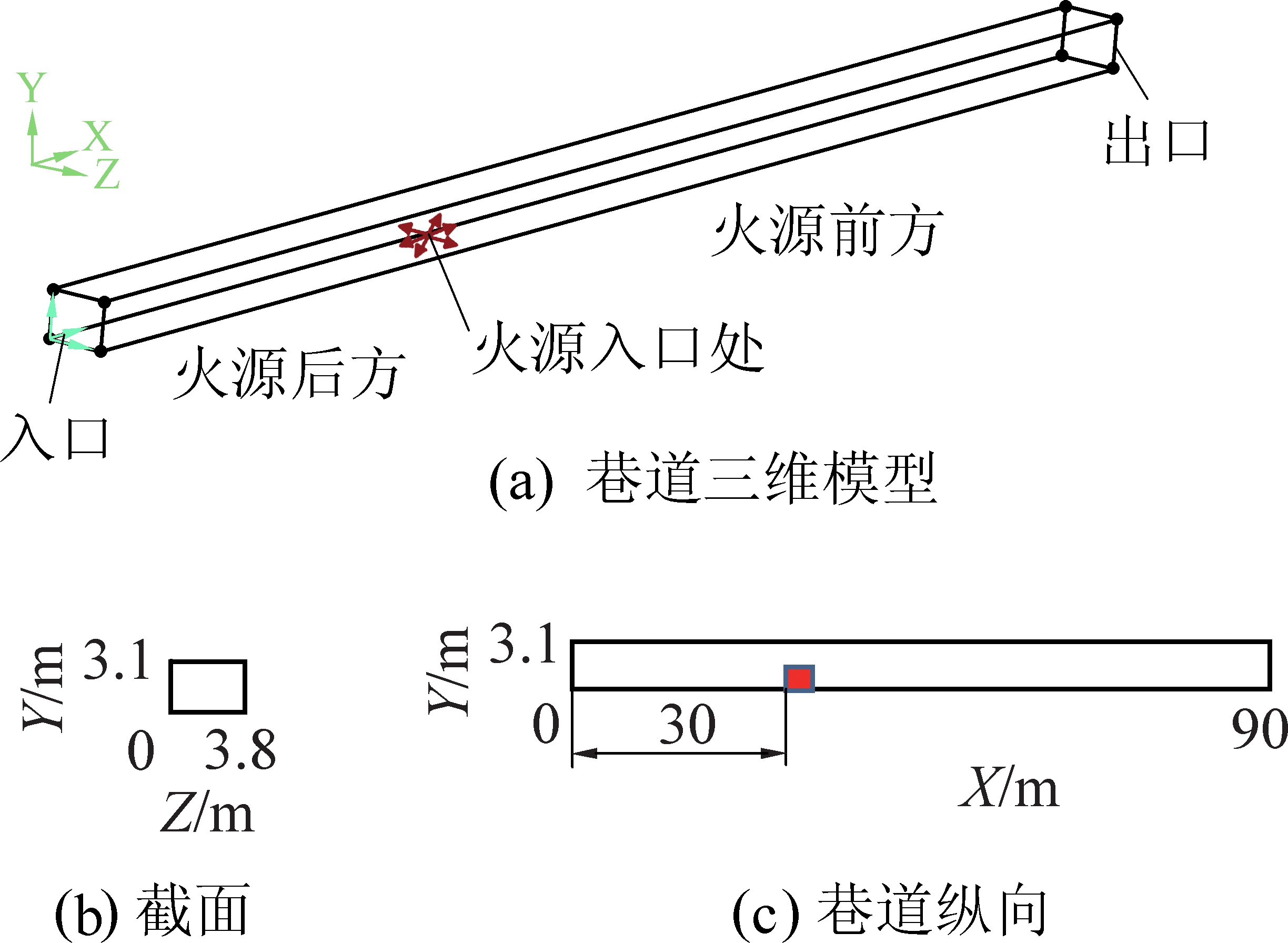
图1 巷道三维模型及纵横截面
Fig.1 Tunnel 3D model and longitudinal and cross section
针对以上模型,使用建模工具Gambit在笛卡尔坐标系下建立模型并对模型划分计算网格,将模型进行结构化网格划分,网格划分间隔为0.1 m,直接对体网格进行划分,巷道内流域划分成158 200个体积单元,共122 738个节点。本模拟中采用六面体网格,此网格在进行计算时产生的误差较小,且计算精度较高,满足网格质量的要求[19]。
气体入口边界设为速度入口(velocity),风流垂直于模拟巷道入口均匀进入巷道。进口物质为空气,由《煤矿安全规程》可知,采煤工作面允许风速为0.25~4.00 m/s[17],故巷道入口速度可分别设置为1、2、3、4 m/s。经计算,水力直径为3.414 m,湍流强度设为5%,入口温度为300 K;火源入口边界设为速度入口(velocity),均匀风流沿巷道内法线方向垂直于入口进入巷道,温度为2 000 K;出口边界设为自由出流(outflow);除入、出口边界外其他边界均设为壁面,并且不参与任何热交换,温度为300 K且壁面无滑移、无渗透[20];厚度设为0 m,壁面的粗糙度取0.03。
瓦斯源项采用SourceTerm来处理瓦斯涌出,经测量该工作面的瓦斯涌出量为32.5 m3/min,瓦斯涌出源项为0.000 36 kg/(m3·s)。
工作面巷道设为fluid,并且里面充满甲烷和空气混合物的不可压缩理想气体。边界条件设定后,采用simple算法,定湍流模型为标准k-epsilon方程模型,启用能量方程,组分运输模型。操作条件设初始压力为101 312 Pa,重力加速度为-9.81 m/s2,初始温度为20 ℃[21]。另外,由于巷道火灾火源设定为固定热源,因此该模拟为定常流动。其中边界条件的主要参数设置如下:

巷道进口速度/(m·s-1)1、2、3、4巷道进口、壁面温度/K300湍流强度/%5火源温度/K2 000初始压力/kPa1.01瓦斯涌出源项/(kg·m-3·s-1)3.6×10-4出口边界类型outflow
矿井巷道发生火灾后,巷道内烟流的速度分布影响着温度和污染物的分布,因此要研究巷道内烟流的速度分布,如图2所示。
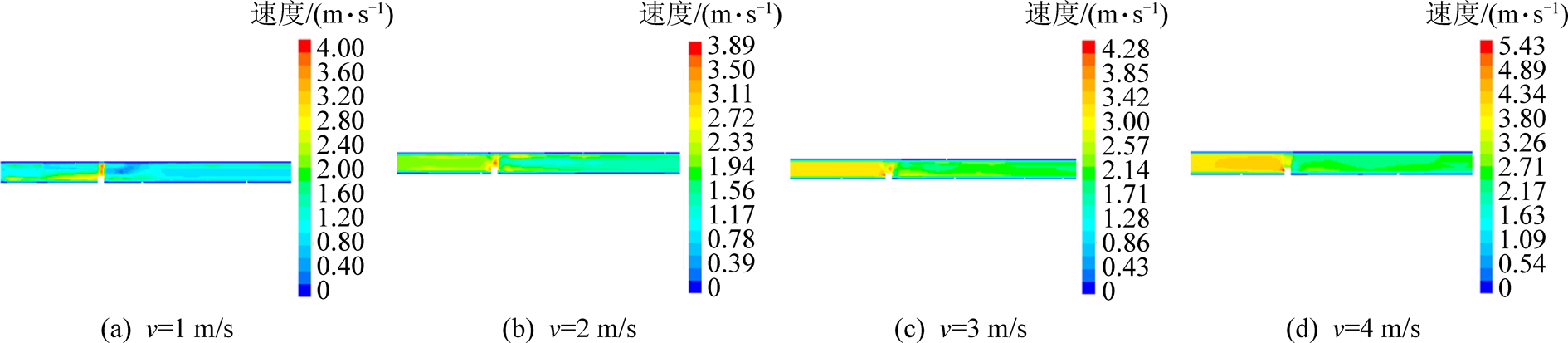
图2 X方向的速度分布云图
Fig.2 Velocity distribution cloud map in X direction
对比图2中各图的速度分布可知,在风速为1 m/s时,火源正上方的温度骤然上升,火源后方地面的速度有一定的升高,其他区域的速度接近入口风速。这主要是火源上方的烟气速度起作用,而入口风速太低,并没有给巷道内风速起到扰动作用。在风速为2、3、4 m/s时,火源后方沿X负方向的风速先是骤然升高,然后又缓慢下降。因为入口风速较大,与火源上方的烟气速度叠加,使火源上方风速达到最大;入口速度较大,使烟气在火源后部扩散较快,速度分布因此越来越接近于正常通风时期,从而使沿X负方向速度又缓慢下降。总的来说井下发生火灾情况下,风速越大,对巷道内风流分布的影响越小。
综合分析得出,图中火源后方的风速始终大于进风流的初始风速,火源后方的速度大于火源前方的速度,这是因为由于火焰的阻挡,使扩散到火源前方的风速很小,与火源产生的烟气速度叠加后的速度也较小。
为了清楚地看出火源上方的速度分布,模拟了火源上方截面的速度分布,如图3所示。在通风风速为1 m/s时巷道截面上风速完全紊乱,而风速为2、3、4 m/s时,截面上的风速分布呈现出一定的规律性:火焰区域速度较低,火焰上方速度分布呈现出“圆弧层状”降低分布并且圆弧顶部不同程度向下凹陷,随着风速的增加,纵向风速减小的梯度增大。并且同一通风风速下截面从上到下的“圆弧”形状不一致。这是因为火焰的阻挡,使火焰内部的速度较低;在火焰最高峰与风流的交界处,由于风流经过,使火焰最上方速度增大,从而有了凹陷的趋势。
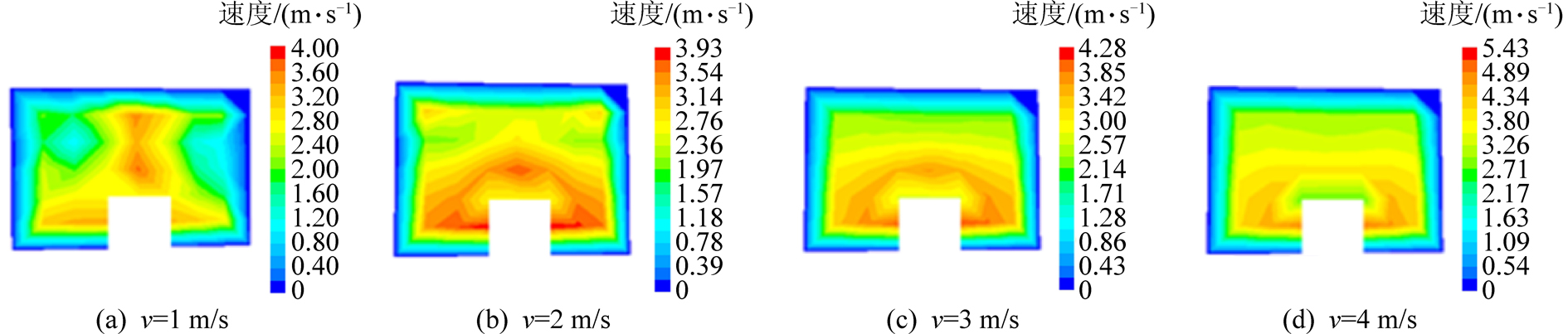
图3 火源上方纵截面的速度分布云图
Fig.3 Velocity distribution cloud map of longitudinal section above fire source
巷道正常通风时期和火灾时期的X方向瓦斯体积分数分布如图4所示。
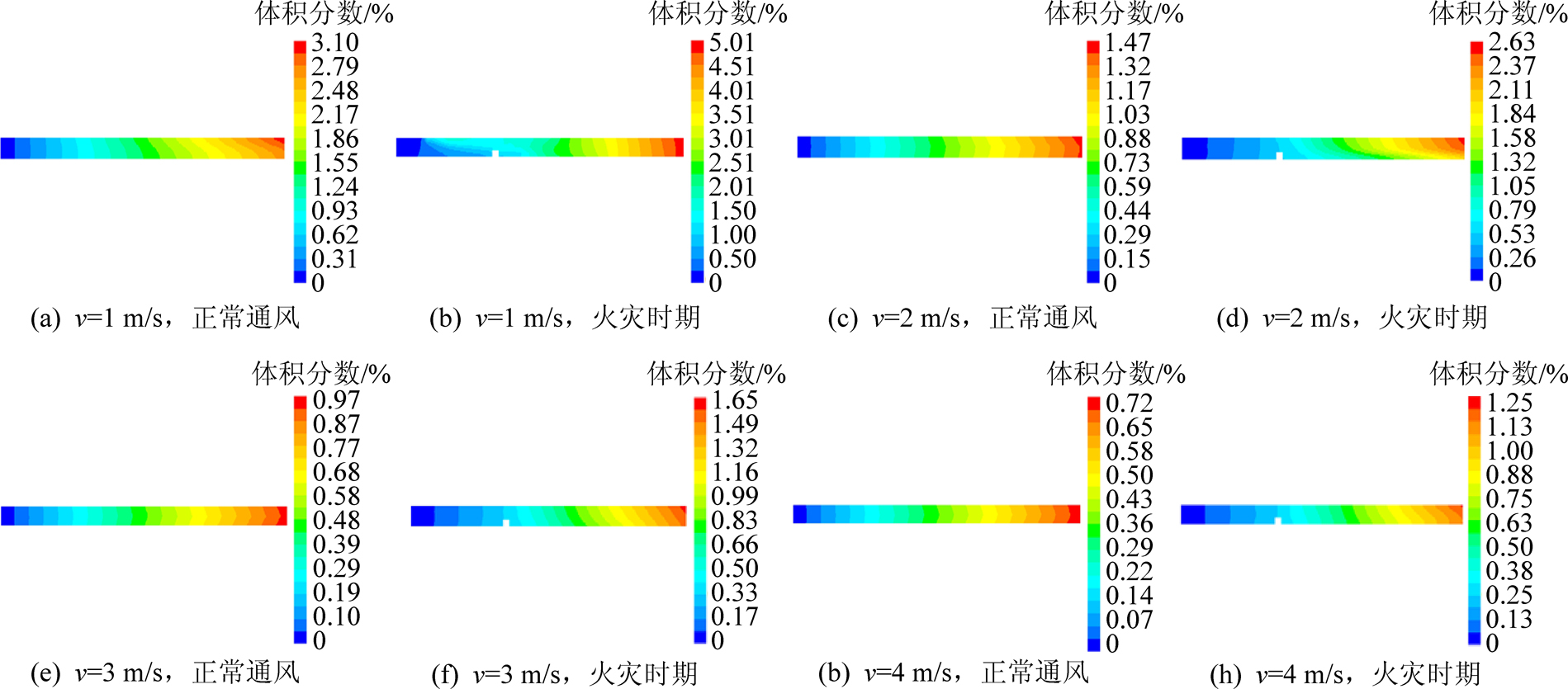
图4 X方向瓦斯体积分数分布
Fig.4 X-direction gas volume fraction distribution
比较图4a、图4c、图4e、图4g不同风速正常通风情况下的瓦斯分布可以发现,靠近巷道入口处,瓦斯浓度较低,随着离入口距离的增大,瓦斯浓度逐渐升高;风量增加1倍时,各点的瓦斯体积分数大约会降低到原来的1/2。风速为1 m/s时,巷道整体的瓦斯浓度较高,仅巷道入口附近的瓦斯体积分数为0.4%以下的正常数值,而之后的浓度都很高,巷道尾部瓦斯体积分数达到了3.1%。所以,想要满足《煤矿安全规程》中规定的出口瓦斯体积分数达1.5%的标准,还需增大风量。风速为2 m/s时,瓦斯体积分数的最大值为1.47%,达到规定的标准,但瓦斯浓度仍然过高。在风速为3、4 m/s时,瓦斯浓度越来越低,正常的瓦斯浓度范围增大,巷道尾部的瓦斯浓度降低明显。风量越大,瓦斯浓度越不容易达到瓦斯爆炸下限浓度。这是由于风量越大,瓦斯与风流混合越充分,风流带走的瓦斯越多,巷道内的瓦斯浓度就低。
比较图4b、图4d、图4f、图4h可以看出,在风速较小时,巷道顶板附近出现了明显的瓦斯逆流现象,且逆流区瓦斯浓度远大于巷道底部的瓦斯浓度,随着风速的增长,瓦斯逆流长度逐渐变短,当风速增到3 m/s时,不再发生瓦斯逆流;当风速为1 m/s时,巷道顶板处瓦斯逆流长度为20 m,风速为2 m/s时,瓦斯流向稍有偏移,大于2 m/s时,巷道顶板不再有瓦斯逆流现象的出现。
由火源前方的瓦斯浓度分布可以看出,巷道上部的瓦斯浓度高于下部,这是因为瓦斯的密度低于空气的密度,在随风流发生纵向运移的同时,有向上运动的趋势,因而巷道断面上部的瓦斯浓度要比下部的高。
通过以上分析得出,将入口风速设为3 m/s最合适,此时正常通风时的瓦斯浓度低且在发生火灾后不会产生瓦斯逆流。由于巷道上部的瓦斯浓度较高,在火灾逃生过程中,要俯身快速逃离现场。
对比同一风速下,火灾时期与正常通风时的瓦斯浓度分布可以发现,同一区域的瓦斯浓度,火灾时期的浓度将近正常通风时的2倍。在风速为1 m/s时,最高的瓦斯体积分数为5.01%,达到瓦斯爆炸下限,在有火源的情况下会引发瓦斯爆炸,将会产生极大危害;在风速为2 m/s时,最高瓦斯体积分数虽然降低了很多,但仍达到2.63%,需要采取处理措施;在风速为3、4 m/s时,整体的瓦斯浓度不高,但巷道尾部的瓦斯体积分数仍超过1%,也要采取相应的措施。火灾引起巷道内瓦斯浓度增大,是因为火灾产生的节流效应[22],水平巷道浮力效应可忽略,而节流效应使巷道内风流引起瓦斯积聚造成瓦斯浓度增高。
巷道内CO会严重破坏工作环境,危害井下工作人员的健康,给矿井通风带来影响[23],因此,要监控分析巷道内CO的分布情况。
X方向CO体积分数分布如图5所示,X方向温度等值线如图6所示。对比两图可以看出,温度等值线分布与CO体积分数分布几乎一致,这是由于火灾产生的烟气量与从巷道出口排出的烟气量达到了动态平衡,使巷道内流场趋于稳定,温度场也趋于稳定[24]。当风速为1 m/s时,靠近火源处烟气温度、CO体积分数最高,烟气扩散趋势为斜偏向巷道顶板的方向,到达顶板后再向巷道两端流动,大部分烟气流向火源前方,产生的烟气充满巷道后部,并且有部分烟气沿火源后部顶板方向流动,产生“烟流滚退”现象[18],火灾烟流将污染火区上游的巷道,威胁火区上游作业人员的生命安全。整个巷道的烟气流动较混乱,不易排出。

图5 X方向CO体积分数分布
Fig.5 X-direction CO volume fraction distribution
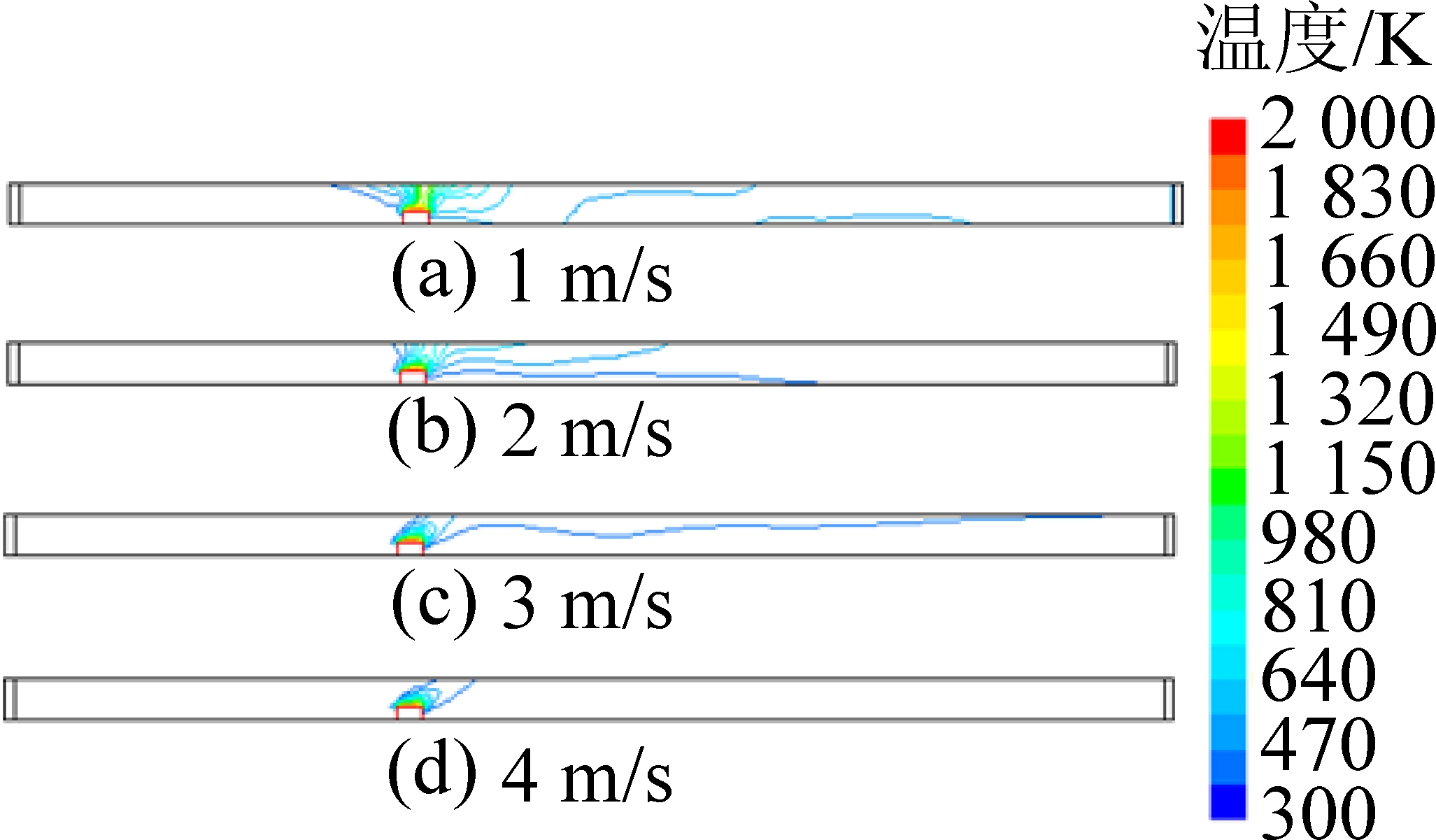
图6 X方向温度等值线分布
Fig.6 X-direction temperature contour distribution
当风速为2 m/s时,烟流滚退距离明显缩短,仅在火源后部略有滚退,产生的烟气基本充满了火源巷道后部,烟气排出效果不显著;当风速为3 m/s时,所有烟气流向巷道出口,不发生烟流滚退,巷道内烟气的温度相对较低,巷道底部的烟气大部分被排出;当风速为4 m/s时,烟气扩散范围很小,都斜偏向了巷道顶端,排烟的效果很显著。说明在其他条件不变的情况下,风速的变化,会使“烟流滚退”距离有较大的改变。因此为了防止烟流滚退的发生,要合理控制巷道入口风速。
通过分析和比较不同风速情况下,巷道内烟气流动的体积分数、温度的分布结果,很容易得出:当巷道内风速较小时,巷道内火灾产生的高温有毒有害烟气不仅对火源前方巷道内空气污染严重,对火源后方巷道也有一定污染。随着巷道内风速增大,排出烟气的速率增大,烟气对火源后方巷道的污染减小,“烟流滚退”现象消失,对火源前方巷道的污染会减轻,烟气浓度有所降低,巷道气流的温度也随之降低,排烟的效果更好。
高温烟气迅速蔓延覆盖巷道其他区域,会引起井下人员的恐慌,一旦温度超过人体承受极限时则会造成人员死亡。为了使火灾后巷道温度定量化,绘制了X方向温度变化折线,如图7所示。

图7 X方向温度变化折线
Fig.7 Line chart of X-direction temperature change
由于巷道入口风流的温度较低,在火源后方的温度没有明显变化,温度为入口风流温度。而在火焰前方距离火源较近的火区,烟流的温度较高,这是因为燃烧产生的高温烟气不断在火源点附近积聚,导致火区温度呈指数增长,而高温烟流和入口低温空气混合又导致温度大幅度下降,因为火源不断释放高温烟流,最后达到稳定状态。火源前方的温度整体要高于火源后方的温度,火源释放的烟流在机械通风、自然通风和火灾动力效应的作用下,向火源前方流动。随着火灾的发展,污染区域的范围不断扩大,由于烟流温度高于井巷周围物体的温度,所以烟流在流动过程中不断与周围的物体进行热交换,热量从烟流流向周围的物体,周围的物体在热能的作用下温度升高[25]。
对比分析图7,发现随着入口端速度的增大,火区达到的稳定温度逐渐变低。所以要适当增加入口风速。为了研究污染物在巷道截面上的分布情况,分别截取了入口风速为1、2、3、4 m/s 时火源点正上方处巷道截面的CO浓度分布,如图8所示。从图中可以看出,在火源正上方,CO以火源为中心向四周扩散,但扩散范围并没有布满整个截面。CO分布呈现中间浓度最大、周边浓度小的特点。总体来说,在距火源不同距离的横截面上,靠近巷道顶部的浓度最先达到最大,巷道两肩浓度较顶部小。
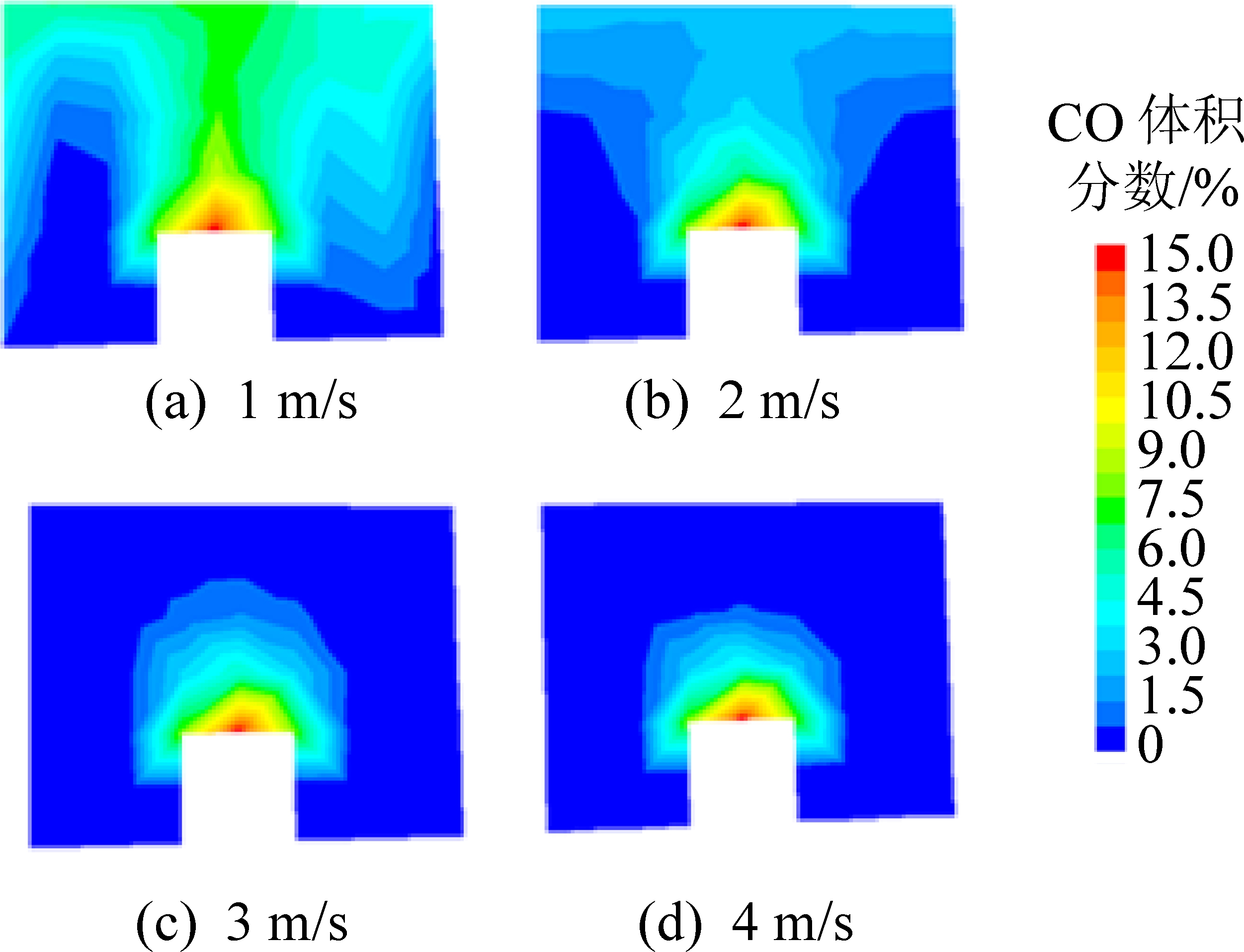
图8 火源上方纵截面的CO浓度分布云图
Fig.8 CO concentration distribution cloud map of the longitudinal section above the fire source
1)发生火灾会引起风流的紊乱,在纵向截面速度分布呈现出“圆弧层状”降低的趋势。井下发生火灾情况下,风速越大,对巷道内风流分布的影响越小。
2)火灾的发生会使巷道内的瓦斯浓度增大约1倍,在风速为1 m/s时,最大瓦斯浓度超过瓦斯爆炸下限5%,在火灾发生时会发生爆炸,风速越低,瓦斯浓度越大,因此要合理控制入口风速。
3)随着巷道内风速增大,排出烟气的速率有所增大,逐步消除对火源后方巷道的污染,“烟流滚退”现象消失,排烟的效果越来越好。
[1] ZHANG S,WU Z,ZHANG R,et al.Dynamic numerical simulation of coal mine fire for escape capsule installation[J].Safety Science,2012,50:600-606.
[2] RAN Vijay,KUMAR Singh.Spontaneous heating and fire in coal mines[J].Procedia Engineering,2013,62:78-90.
[3] SONG Z,KUENZERC.Coal fires in China over the last decade:A comprehensive review[J].International Journal of Coal Geology,2014,133:72-99.
[4] 安敬鱼,牛会永,邓 军,等.矿井火灾原因综合分析及防治技术[J].矿业工程研究,2015,30(3):40-44.
AN Jingyu,NIU Huiyong,DENG Jun,et al.Comprehensive causes and treatment technology of mine’s fire[J].Mineral Engineering Research,2015,30(3):40-44.
[5] 王 凯,蒋曙光,张卫青,等.矿井火灾应急救援系统的数值模拟及应用研究[J].煤炭学报,2012,37(5):857-862.
WANG Kai,JIANG Shuguang,ZHANG Weiqing,et al.Numerical simulation and application research of mine fire emergency rescue system[J].Journal of China Coal Society,2012,37(5):857-862.
[6] 梁 栋.矿内瓦斯运移规律及其应用[D].北京:中国矿业大学(北京),1996.
[7] ZHANG Q,QIN B,YAN,H,et al.A methodology to predict shock over pressure decay in a tunnel produced by a premixed methane/air explosion[J].Loss Prevention in the Process Industries,2016,44:275-281.
[8] 高建良,王春霞,徐昆伦.贯通巷道风流流场数值模拟若干关键问题研究[J].中国安全科学学报,2009,19(8):21-27,177.
GAO Jianliang,WANG Chunxia,XU Kunlun.Research of several key problemsin numerical simulation of flow field of airway[J].China Safety Science Journal,2009,19(8):21-27,177.
[9] 程卫民,姚玉静,吴立荣,等.基于Fluent的矿井火灾时期温度及浓度分布数值模拟[J].煤矿安全,2012,43(2):20-24.
CHENG Weimin,YAO Yujing,WU Lirong,et al.Fluent-based numerical simulation of temperature and concentration during mine fire[J].Safety in Coal Mines,2012,43(2):20-24.
[10] 苏传荣,王海燕.矿井掘进巷道火灾数值模拟研究[C]//2006(沈阳)国际安全科学与技术学术研讨会论文集,2006.
[11] HARLOWF H,WELCH J E.Numerical calculation of time-dependent viscous incompressible flow of fluid with free surface[J].Physics of Fluids,1965,8(12):2182.
[12] 马洪亮,周心权,王 轩.多单元区域方法在矿井火灾模拟中的应用[J].煤炭科学技术,2008,36(1):62-64,81.
MA Hongliang,ZHOU Xinquan,WANG Xuan.Application of multi element area method to mine fire disaster simulation[J].Coal Science and Technology,2008,36(1):62-64,81.
[13] 周西华,王继仁,卢国斌,等.回采工作面温度场分布规律的数值模拟[J].煤炭学报,2002,27(1):59-63.
ZHOU Xihua,WANG Jiren,LU Guobin,et al.The numerical simulation of distribution law of temperature field in coal face[J].Journal of Coal Society,2002,27(1):59-63.
[14] 王文才,乔 旺,李 刚,等.矿井巷道火灾烟流运动理论研究[J].工矿自动化,2011,37(3):22-25.
WANG Wencai,QIAO Wang,LI Gang,et al.Research of movement theory of fire smoke flow of mine roadway[J].Industry and Mine Automation,2011,37(3):22-25.
[15] 史文芳.矿井火灾烟气流动及温度分布规律数值模拟研究[D].太原:太原理工大学,2013.
[16] 何学秋.中国煤矿灾害防治理论与技术[M].徐州:中国矿业大学出版社,2006.
[17] 秦跃平,王 浩,郭开元,等.巷道围岩温度场有限体积法模拟计算及实验分析[J].煤炭学报,2017,42(12):3166-3175.
QIN Yueping,WANG Hao,GUO Kaiyuan,et al.Simulation of finite volume method and experimental analysis for temperature field of roadway surrounding rock[J].Journal of China Coal Society,2017,42(12):3166-3175.
[18] 丁 翠.矿井巷道风流状态“关键环”实验与数值研究[D].北京:中国矿业大学(北京),2013.
[19] 李文蜜.六面体和三棱柱网格形态对煤矿开采沉陷数值模拟的影响研究[D].北京:中国地质大学(北京),2013.
[20] RYBDYLOVA O,POULTON L,AL QUBEISSI M,et al.A model for multi-component droplet heating and evaporation and its implementation into ANSYS Fluent[J].International Communications in Heat and Mass Transfer,2018,90:29-33.
[21] 张辛亥,丁 峰,张玉涛,等.井下烟道在巷道火灾中的作用数值模拟[J].煤矿安全,2017,48(4):48-51.
ZHANG Xinhai,DING Feng,ZHANG Yutao,et al.Numerical analysis of underground flue effect on mine roadway fire[J].Safety in Coal Mines,2017,48(4):48-51.
[22] 朱海刚,周心权,姜 伟,等.矿井火灾对巷道瓦斯积聚影响的研究[J].矿业安全与环保,2008,35(3): 18-20,91.
ZHU Haigang,ZHOU Xinquan,JIANG Wei,et al.Study on the influence of mine fire on gas accumulation in roadway[J].Mining Safety & Environmental Protection,2008,35(3): 18-20,91.
[23] 齐庆杰,赵尤信,李兴华.采空区CO涌出量预测模型[J].煤炭科学技术,2018,46(2):182-186.
QI Qingjie,ZHAO Youxin,LI Xinghua,et al.Prediction modal of CO emission volume from goaf[J].Coal Science and Technology,2018,46(2):182-186.
[24] 陈 亮,邬长福,陈祖云,等.矿井巷道火灾安全区域划分数值模拟[J].消防科学与技术,2016,35(5): 633-636.
CHEN Liang,WU Changfu,CHEN Zuyun,et al.Numerical simulation of fire safety zone division in mine roadway[J].Fire Science and Technology,2016,35(5): 633-636.
[25] 贾进章,马 恒,刘 剑.矿井火灾时期温度分布数值模拟研究[J].辽宁工程技术大学学报,2003,22(4):35-41.
JIA Jinzhang,MA Heng,LIU Jian.Numerical simulation for temperature distribution during mine fire period[J].Journal of Liaoning Technical University,2003,22(4):35-41.