0 引言
露天矿的岩石剥离及矿石回采工程多采用穿孔爆破方法进行预先破碎,与机械破碎、热力破碎等方法相比,其优势是爆破量大,可破碎十分坚硬的矿岩,因而应用最为广泛[1]。矿岩爆破破碎的效果对采装、运输、破碎等生产环节效率影响很大,如:矿岩破碎后不合格的大块需进行二次破碎,提高了穿爆成本,且影响装车效率;而有用矿物的过度粉碎,则会影响产品质量,降低其经济效益[2]。为了保证爆破质量,需在爆破施工前对矿山待爆岩体作科学准确的评价,岩体可爆性是岩体抵抗爆破破碎的能力,是岩体坚固性在爆破方面的综合体现,能够反映岩体爆破破碎的难易程度[3-5]。对岩体可爆性进行分级是优化爆破参数、计算炸药单耗的重要依据,有利于提高爆破质量,降低生产成本[6-8]。
为了对岩体可爆性进行科学分级,几十年来,国内外学者进行了大量的研究,也取得了丰硕的成果。目前,岩体可爆性分级有2大类方法,第1类采用岩石普氏系数、破碎功指数、岩石可爆性指数等单一综合指标进行可爆性分级。如东北大学岩石爆破性分级科研组在能量平衡准则的基础上,提出了岩石爆破性指数来综合评价岩石的可爆性的方法[9]。第2类采用集对分析、模糊综合评价、神经网络、聚类分析、物元可拓法、属性识别、灰色关联分析、模糊识别等评价方法进行可爆性分级。李涛等[10]选取平均裂隙间距、岩体普氏系数、岩体波阻抗、动弹性模量为评价指标,建立了岩体可爆性分级的粗糙元神经网络模型;袁绍国等[11]选择岩体的容重、抗拉强度、抗压强度和完整性系数作为岩体可爆性评判参数,建立了基于集对分析的可爆性分级模型。邓红卫等[12]选取岩石的容重、抗拉强度、动载强度及岩体完整性系数等指标,建立了岩体可爆性等级判别的随机森林模型;尚俊龙等[13]建立了可爆性分级的博弈论-物元可拓预测模型;薛剑光等[14]利用Shannon熵理论客观地确定了可爆性评价指标的熵权系数,并结合属性识别理论,建立了岩体可爆性分级判别的属性识别模型。由于岩体可爆性受诸多因素影响,复杂性、模糊性、随机性大,较难采用单一指标综合反映岩体可爆性。综合评价方法各有优缺点,以上方法较难同时反映岩体可爆性的模糊性、随机性,较难给出分级结果的可靠性。
基于此,笔者提出一种基于综合赋权与云模型的岩体可爆性分级方法,利用云模型突出可爆性分级结果的随机性和模糊性,为岩体可爆性分级提供了一种新思路。
1 岩体可爆性分级指标体系
1.1 分级指标选取
岩体可爆性受岩石物理力学性质、岩体的地质构造特征的影响,可反映岩体可爆性的指标较多,但为了保证可爆性分级方法的简单实用,不可能选择所有指标作为可爆性的分级指标,应该选择不相关或者相关性较低、易测、具有代表性的少数指标。根据以上原则,参考相关文献[15-16],本文选择岩石普氏系数f、抗拉强度σt、岩石密度ρ、岩石纵波速度vpr、岩体纵波速度vpm五个指标作为岩体可爆性分级指标。
1)岩石普氏系数与抗拉强度。通常认为炸药爆炸作用使岩体在拉、压等作用下破碎,因此,岩石的抗压强度、抗拉强度是影响其可爆性的重要指标。岩石的动载强度可更真实反映可爆性,但动载强度难以测量,而动载强度与岩石单轴静载抗压强度、抗拉强度高度相关,岩石普氏系数由岩石的单轴抗压强度确定,且应用更为广泛,因此选择岩石普氏系数、抗拉强度作为分级指标。
2)岩石密度。通常,岩石密度越大,岩石位移、抛掷运动所需能量越多,岩体越难爆破,因此普遍选择岩石密度作为可爆性分级指标。
3)岩石纵波速度、岩体纵波速度。岩石纵波速度可以反映其矿物成分、孔隙性、风化程度等物理性质,根据岩石的密度与纵波速度可以计算得出岩石的波阻抗,波阻抗可体现岩石抵抗动量传递的能力。
岩体纵波波速能够反映岩体的完整性、裂隙性等地质特征,利用岩体纵波速度、岩石纵波速度可计算得到岩体完整性系数,岩体完整性系数反映岩体裂隙发育程度,岩体完整性系数越大,说明岩体越完整,岩体越难爆破。
2.2 分级标准确定
参考相关文献资料中的分级标准, 将岩体可爆性划分为极易爆、易爆、中等、难爆和极难爆5个等级,可爆性分级标准见表1。
表1 可爆性分级标准
Table 1 Classification standards of blastability

可爆性等级fσt/MPaρ/(t·m-3)vpr/(m·s-1)vpm/(m·s-1)可爆性描述A≤2.5≤1.5≤2.00≤2000≤700极易爆B2.5~6.01.5~3.02.0~2.42000~3000700~1500易爆C6.0~10.03.0~6.02.4~2.73000~40001500~2400中等D10.0-18.06.0-12.02.7-3.04000~50002400~3500难爆E≥18.0≥12.0≥3.0≥5000≥3500极难爆
2 岩体可爆性分级云模型
2.1 云模型原理
1)基本概念及其数字特征。云模型是由李德毅院士结合概率论与模糊数学理论提出的处理定量数值与定性概念不确定转换的数学模型,它能够有效解决模糊概念定量化问题,已被应用于军事、通信、教育、农业等领域[17]。
假设U是用数值表示的定量论域,C是定量论域U上的定性概念,若定量值x∈U是C的一次随机实现,则x对C的确定度μ(x)∈[0,1]是具有稳定倾向的随机数,则x在U上的映射在数域上的分布简称为云,每个x称为一个云滴。
云的数字特征反映定性概念的定量特征,用期望Ex、熵En、超熵He表征。期望Ex是论域空间的中心值,是论域空间最具代表性的定性概念值。熵En是各指标定性程度的度量,由定性概念的模糊性与随机性共同确定。超熵He是熵的不确定性度量,超熵He越大,云的厚度亦越大。期望Ex、熵En、超熵He可按表2计算[18]。
表2 数字特征计算方法
Table 2 Calculation method of numerical characteristics

可爆性等级指标区间ExEnHeA(0,a)Ex1=(0+a)/2En1=(a-0)/60.01B(a,b)Ex2=(a+b)/2En2=(b-a)/60.01C(b,c)Ex3=(b+c)/2En3=(c-b)/60.01D(c,d)Ex4=(c+d)/2En4=(d-c)/60.01E(d,+∞)Ex5=dEn5=En40.01
2)云发生器。云发生器是云模型建立定性与定量间关系的工具,主要有正向云、逆向云、条件云三种,正向云发生器输入数字特征Ex、En、He以及云滴数n,输出所有云滴的分布及每个云滴的确定度,即可将评价指标的定性特征转换为定量数值,而逆向云发生器则相反。本文采用目前广泛使用的正向正态云发生器产生云模型[19]。x对定性概念C的确定度μ(x)可按式(1)计算:
(1)
其中:x~N(Ex,En′2);En′~N(Ex,En2)。
3)云模型生成步骤。正向正态云模型的生成步骤如下:① 生成期望为En,标准差为He的正态随机数En';② 生成期望为Ex,标准差为En'的正态随机数xi;③ 利用式1计算μ(xi),得云滴(xi,μ(xi));④ 重复以上3个步骤,直到生成N个云滴;⑤ 由所得N个云滴生成云图。
2.2 博弈论综合赋权
计算权重的常用方法有主观赋权法、客观赋权法2大类。主观赋权法根据专家对指标的评判进行赋权,具有较大的主观性;客观赋权法依据各指标差异程度计算权重,需要较多样本数据,且未考虑研究问题的实际背景。为此,本文采用层次分析法计算主观权重,采用熵权法计算客观权重,采用博弈论综合赋权法将主观、客观权重进行优化,博弈论综合赋权步骤如下[20-21]:
假设采用L种方法计算指标权重,权重向量Wk=(ωk1,ωk2,…,ωkn)(k=1,2,…,L,n为指标个数)。将L个权重向量进行线性组合构成综合权重向量为
(2)
式中:Wc为综合权重向量;αk为组合系数,αk>0。
使Wc与Wk的离差极小化,从而对组合系数αk进行优化,即对策模型为
(3)
利用矩阵的微分性质求得式(3)的最优化一阶导数条件为
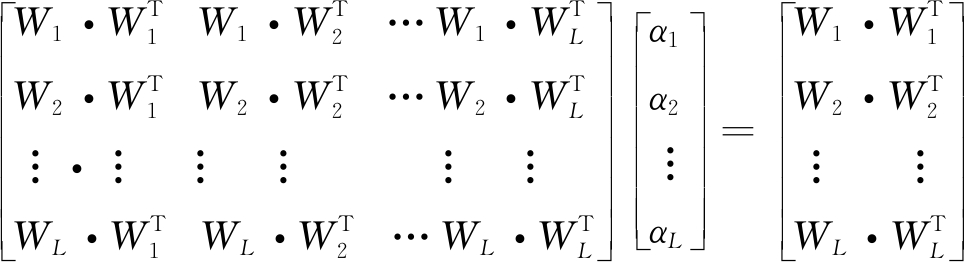
(4)
计算得(α1,α2,…,αL),并利用式(5)进行归一化处理,得优化的组合系数![]() 为
为
(5)
优化的综合权重向量为
(6)
2.3 可爆性分级模型
假设岩体可爆性划分为m(m=5)个等级,岩体可爆性分级指标个数为n(n=5)。可爆性分级模型建立流程如图1所示,详细步骤如下:
1)根据表1中的岩体可爆性分级标准与表2中的数字特征计算公式计算可得岩体可爆性分级指标的云数字特征。
2)利用Matlab软件编写正向正态云发生器,将计算的各分级指标的数字特征输入发生器,可生成各指标隶属各岩体可爆性等级的云模型,如图2所示。
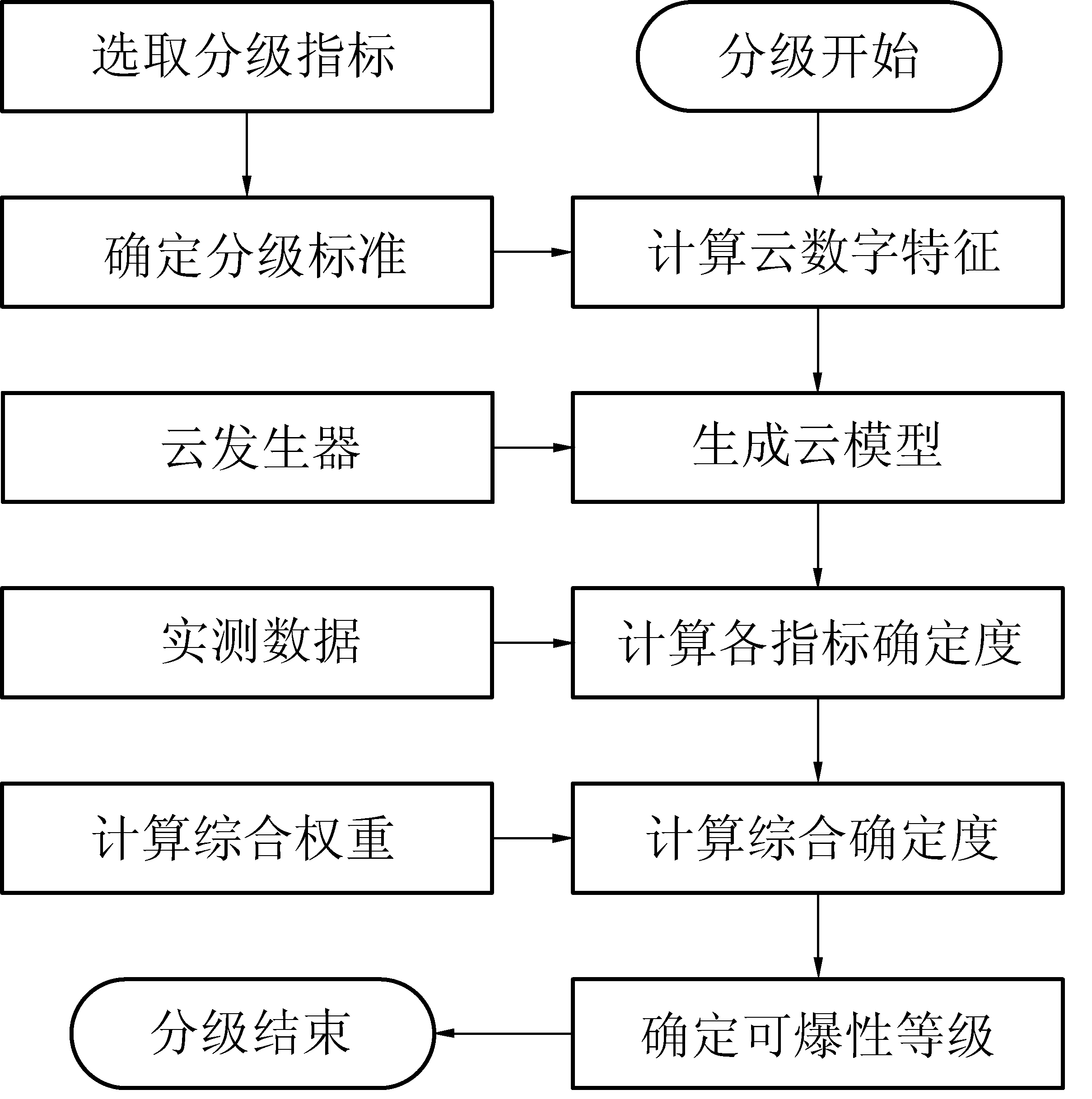
图1 岩体可爆性分级流程
Fig. 1 Flow of rock mass blastability classification
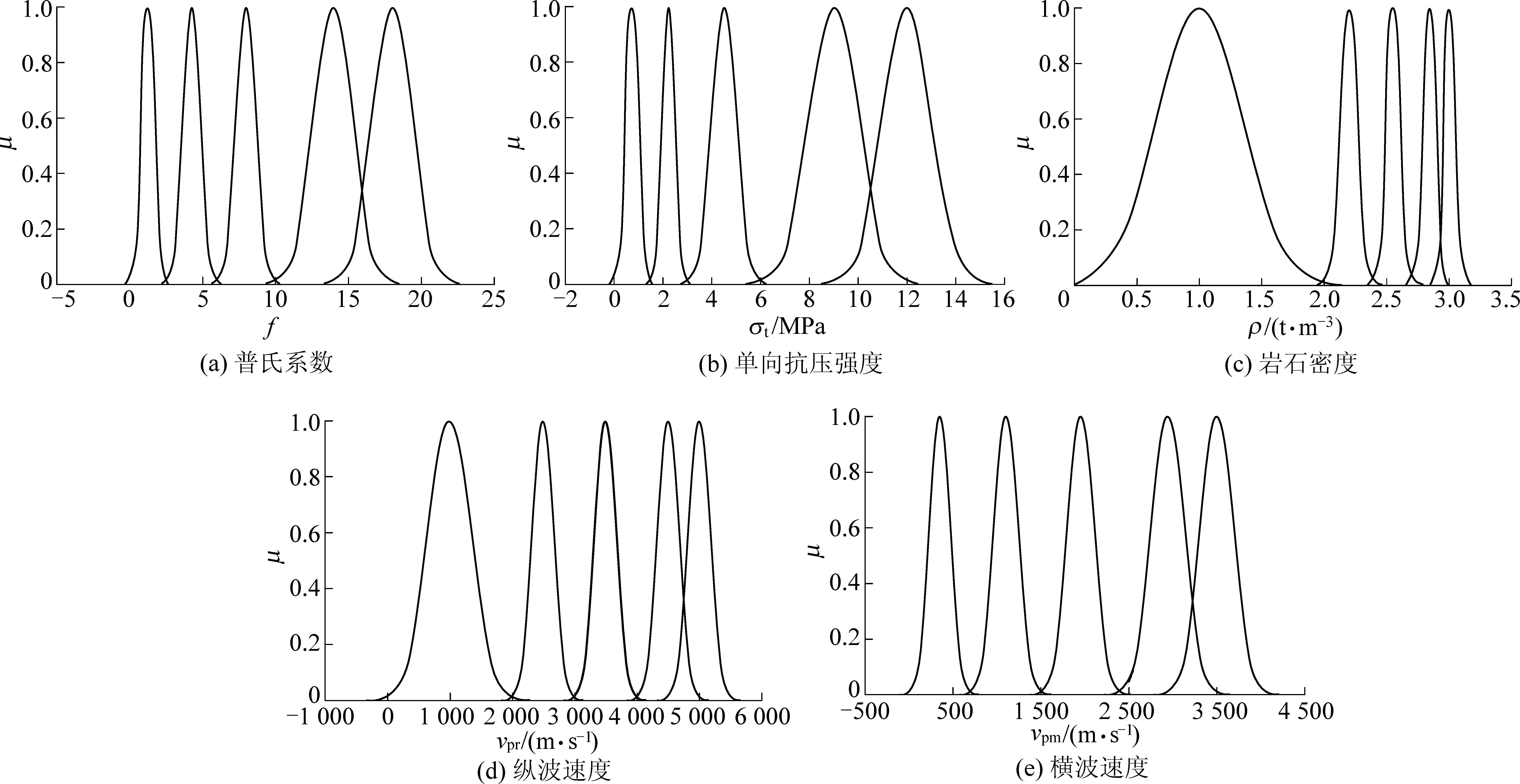
图2 岩体可爆性云模型分级
Fig.2 Cloud model of rock mass blastability classification
从图2可知,横坐标为指标取值,纵坐标为指标对应可爆性等级的确定度。由生成的岩石普氏系数云模型可以看出,岩石普氏系数5个等级间的界限不明显,相同的岩石普氏系数可隶属于不同可爆性等级。因此,云模型体现了“亦此亦彼”性,同时又具有随机性,从而可揭示客观对象的模糊性和随机性。
3)根据实际数据,利用正向正态云发生器,根据式1计算出各指标隶属于各可爆性等级的确定度μij(i=1,2,…,m;j=1,2,…,n)。
4)统计样本数据,分别利用层次分析法、熵权法计算主、客观权重,利用式(2)—式(6)计算综合权重。
5)利用综合权重计算综合确定度为
(7)
式中,μi为岩体对第i等级的综合确定度(i=1,2,…,m);μij为第j指标对第i等级的确定度![]() 为第j个指标的综合权重。
为第j个指标的综合权重。
6)利用式8确定岩体的可爆性等级为
p=max{μi|i=1,2,…,m}
(8)
3 工程应用
以中煤平朔集团有限公司东露天煤矿为例,由于未对岩体可爆性进行准确分级,根据工程经验进行爆破设计,导致平均炸药单耗、爆破成本偏高。为了实现爆破环节的降本增效,对露天矿主要岩石物理力学性质进行了测试,结果见表3。
表3 测试结果
Table 3 Test results
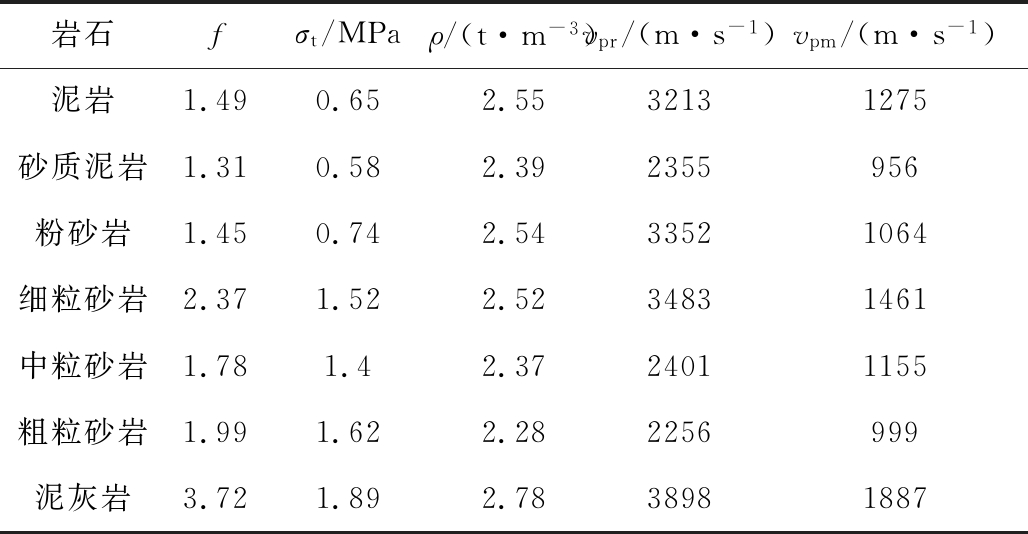
岩石fσt/MPaρ/(t·m-3)vpr/(m·s-1)vpm/(m·s-1)泥岩1.490.652.5532131275砂质泥岩1.310.582.392355956粉砂岩1.450.742.5433521064细粒砂岩2.371.522.5234831461中粒砂岩1.781.42.3724011155粗粒砂岩1.991.622.282256999泥灰岩3.721.892.7838981887
利用层次分析法计算各指标权重向量W1=(0.27,0.14,0.19,0.09,0.31),利用熵权法计算各指标权重W2=(0.32,0.43,0.02,0.10,0.13)。利用式(2)—式(6)计算综合权重向量为
W*=(0.31,0.35,0.06,0.10,0.18)
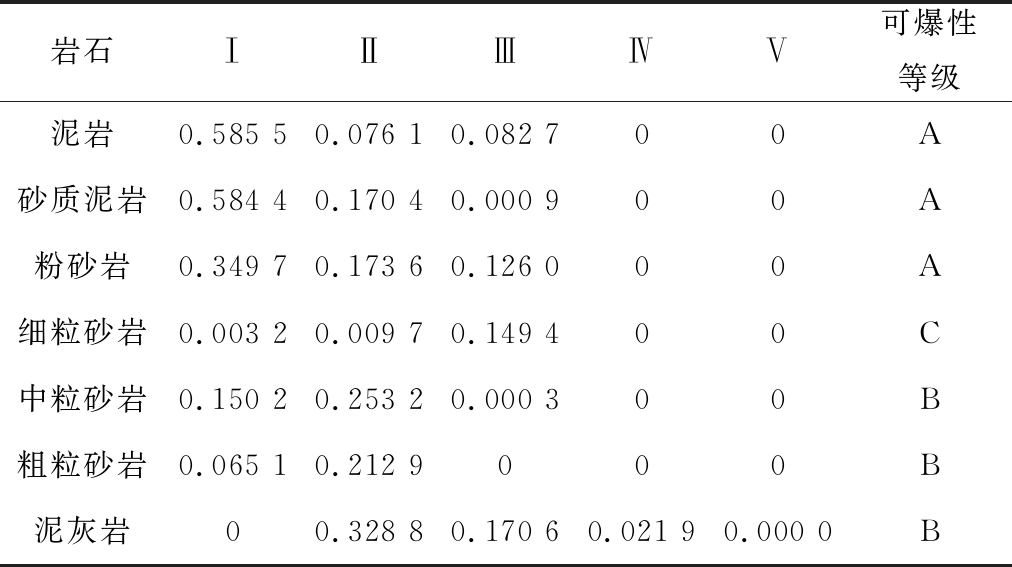
将表3中数据输入正向正态云发生器,可计算出各岩体指标隶属于各可爆性等级的确定度。利用式7计算出综合确定度,结果见表4。
表4 岩体可爆性分级计算结果
Table 4 Results of rock mass blastability classification
岩石ⅠⅡⅢⅣⅤ可爆性等级泥岩0.58550.07610.082700A砂质泥岩0.58440.17040.000900A粉砂岩0.34970.17360.126000A细粒砂岩0.00320.00970.149400C中粒砂岩0.15020.25320.000300B粗粒砂岩0.06510.2129000B泥灰岩00.32880.17060.02190.0000B
基于云模型的岩体可爆性分级方法中的确定度能够精确反映各岩体与各可爆性等级间的隶属程度,有利于更准确地计算炸药单耗,结论的可信度及实用性更高。根据分级结果进行的松动爆破设计取得了较好的爆破效果。
4 结论
露天矿爆破作业是影响露天矿采、运、排环节工作效率和生产成本的一个重要影响因素。以露天矿主要剥离岩层为研究对象,通过分析岩石的物理力学性质及岩体的结构特征对岩体可爆性的影响,建立露天矿岩体可爆性评价模型,主要结论如下:
1)选择岩石普氏系数、抗拉强度、岩石密度、岩石纵波速度、岩体纵波速度5个指标作为岩体可爆性分级指标,这5个指标可较全面的反映岩体的可爆性,指标相关性较低且容易测得。
2)利用云模型建立岩体可爆性分级模型,该模型可实现定量数值与定性概念的不确定转换,在解决模糊性、随机性问题方面体现出较大优势,能够有效处理岩体可爆性分级这一不确定问题。
3)根据东露天煤矿各岩体的相关指标,利用建立的岩体可爆性分级云模型,计算得到了各岩体对各可爆性等级的确定度,并确定了各岩体的可爆性等级。泥岩、砂质泥岩、粉砂岩的可爆性等级为A;中粒砂岩、粗粒砂岩、泥灰岩的可爆性等级为B,细粒砂岩的可爆性为C。
[1] 张 萌. 露天矿爆破工程[M]. 徐州:中国矿业学院出版社, 1986.
[2] 丁小华. 露天矿安全高效爆破理论与智能分析算法[M]. 徐州: 中国矿业大学出版社, 2018.
[3] XIAO Shuangshuang, LI Kemin, DING Xiaohua,et al. Rock mass blastability classification using fuzzy pattern recognition and the combination weight method[J]. Mathematical Problems in Engineering,2015(1): 1-11.
[4] 杨 凯, 时 磊, 黄 滚, 等. 费歇尔判别法在岩体可爆性分级中的应用[J]. 矿业研究与开发, 2018, 38(8): 88-91.
YANG Kai, SHI Lei, HUANG Gun,et al. Application of Fisher discriminate method in blastability classification of rock mass[J]. Mining Research and Development, 2018, 38(8): 88-91.
[5] AZIMI Y, OSANLOO M, AAKBARPOUR Shirazi M,et al. Predication of the blastability designation of rock masses using fuzzy sets[J]. International Journal of Rock Mechanics and Mining Science, 2010, 47(7): 1126-1140.
[6] 彭亚雄, 程 瑶,吴 立, 等. 基于AHP-TOPSIS法的矿岩可爆性评价[J]. 爆破, 2017, 34(4): 84-88, 109.
PENG Yaxiong, CHENG Yao, WU Li,et al.Assessment forore-bearing rock mass blastability based on AHP-TOPSIS[J]. Blasting, 2017, 34(4): 84-88, 109.
[7] 严荣富, 黄温钢, 王清亚, 等. 基于脆性指标与物元理论的可爆性分级技术与应用[J]. 中国矿业, 2018, 27(1): 154-159.
YAN Rongfu, HUANG Wengang, WANG Qingya,et al. The technology and application of blastability classification based on brittleness index and matter element theory[J]. China Mining Magazine, 2018, 27(1): 154-159.
[8] REN Zhanying, XIAO Shuangshuang, LI Kemin et al. Classification of rock mass blastability based on set pair analysis[J]. The Electronic Journal of Geotechnical Engineering, 2014, 14(S1): 1-14.
[9] 东北工学院岩石爆破性分级科研组. 我国矿山岩石爆破性分级的研究[J]. 爆破, 1984, 1(1): 20-22.
Rock Blasting Classification Research Group of Northeast Institute of Technology. Study on blasting classification of mine rocks in China[J]. Blasting, 1984, 1(1): 20-22.
[10] 李 涛, 李克民, 丁小华, 等. 岩体可爆性评价研究与工程应用实例[J]. 矿业研究与开发, 2011, 31(4): 107-109.
LI Tao, LI Kemin, DING Xiaohua, et al.Study of rock blastability evaluation and an example of engineering application[J]. Mining Research and Development,2011, 31(4): 107-109.
[11] 袁绍国, 耿 荣, 王振涛, 等. 基于集对分析的岩体可爆性研究[J]. 煤炭技术, 2018, 37(2): 18-20.
YUAN Shaoguo, GENG Rong, WANG Zhentao, et al. Study of rock mass blastability based on set pair analysis[J]. Coal Technology, 2018, 37(2): 18-20.
[12] 邓红卫, 陈超群, 张亚南. 岩体可爆性等级判别的随机森林模型及R实现[J]. 世界科技研究与发展, 2016(5): 946-949.
DENG Hongwei, CHEN Chaoqun, ZHANG Yanan. Random forest model of rock mass blastability grading and R language implementation[J]. World Sci-Tech R&D, 2016(5): 946-949.
[13] 尚俊龙, 胡建华, 莫荣世, 等.可爆性分级的博弈论 物元可拓预测模型及其应用[J]. 采矿与安全工程学报, 2013, 30(1): 86-92.
SHANG Junlong, HU Jianhua, MO Rongshi, et al.Predication model of game theory-matter-element extension for blastability classification and its application[J]. Journal of Mining & Safety Engineering, 2013, 30(1): 86-92.
[14] 薛剑光, 周 健, 史秀志, 等. 基于熵权属性识别模型的岩体可爆性分级评价[J].中南大学学报:自然科学版, 2010, 41(1): 251-256.
XUE Jianguang, ZHOU Jian, SHI Xiuzhi, et al. Assessment of classification for rock mass blastability based on entropy coefficient of attribute recognition model[J]. Journal of Central South University:Science and Technology, 2010, 41(1): 251-256.
[15] 璩世杰, 辛明印, 毛市龙, 等. 岩体可爆性指标的相关性分析[J]. 岩石力学与工程学报, 2005, 24(3): 468-473.
QU Shijie, XIN Mingyin, MAO Shilong, et al. Correlation analyses of blastability indexes for rock mass [J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(3):468-473.
[16] 璩世杰, 毛市龙, 吕文生, 等. 一种基于加权聚类分析的岩体可爆性分级方法[J]. 北京科技大学学报, 2006, 8(4): 324-329.
QU Shijie, MAO Shilong, LYU Wensheng, et a1. A method for rock mass blastability classification based on weighted clustering analysis[J]. Journal of University of Science and Technology Beijing, 2006, 8(4): 324-329.
[17] 关晓吉. 基于可拓联系云模型的隧道塌方风险等级评价方法[J]. 中国安全生产科学技术, 2018, 14(11): 188-194.
GUAN Xiaoji.Evaluation method on risk grade of tunnel collapse based on extension connection cloud model[J]. Journal of Safety Science and Technology, 2018, 14(11): 188-194.
[18] 黄仁东, 吴 寒, 张 惕, 等. 基于云模型的岩溶隧道涌水灾害危险性评价及其在青岩头隧道的应用[J]. 中国地质灾害与防治学报, 2018, 29(5): 50-57.
HUANG Rendong, WU Han, ZHANG Ti, et al.Evaluation of water burst hazard in karst tunnel based on cloud model and its application in Qingyantou tunnel[J]. The Chinese Journal of Geological Hazard and Control, 2018, 29(5): 50-57.
[19] 曹 琛, 李会中, 陈剑平, 等. 基于组合赋权法与云模型坝基岩体质量评价[J]. 东北大学学报:自然科学版, 2017, 38(11): 1643-1647.
CAO Chen, LI Huizhong, CHEN Jianping, et al. Rock quality evaluation of dam foundation based on component and cloud model weighting method[J]. Journal of Northeastern University:Natural Science , 2017, 38(11): 1643-1647.
[20] 迟道才, 马 涛, 李 松. 基于博弈论的可拓评价方法在灌区运行状况评价中的应用[J]. 农业工程学报, 2008, 24(8): 36-39.
CHI Daocai, MA Tao, LI Song.Application of extension assessment method based on game theory to evaluate the running condition of irrigation areas[J]. Transactions of the Chinese Society of Agricultural Engineering, 2008, 24(8): 36-39.
[21] 山成菊, 董增川, 樊孔明, 等. 组合赋权法在河流健康评价权重计算中的应用[J]. 河海大学学报:自然科学版, 2012, 40(6): 622-628.
SHAN Chengju, DONG Zengchuan, FAN Kongming, et al.Application of combination weighting method to weight calculation in river health evaluation[J]. Journal of Hohai University: Natural Sciences, 2012, 40(6): 622-628.
