Study on mechanism and response of fracture and movement of the far-field high-position hard-and-hick stratum
-
摘要:
掌握远场高位厚硬岩层破断运动规律对于地表剧烈沉降、强矿震等灾害安全防控具有重要作用。以营盘壕煤矿2201、2202工作面为研究背景，建立远场高位厚硬岩层破断力学模型，采用符拉索夫厚板理论分析白垩系砂岩组破断运动规律及其影响因素，并通过地表沉陷、微震响应规律进行验证分析。得出如下结论：①针对白垩系砂岩距煤层远、厚度大、整体性好的赋存特征，建立了远场高位厚硬岩层破断力学模型，采用符拉索夫厚板理论解算出了高位厚硬岩层初次破断临界力学条件。②随着抗拉强度增大，厚硬岩层破断悬露长度依次呈现缓慢增长、线性增长和指数型增长特征；随岩层厚度增大，厚硬岩层破断悬露长度近似呈现指数型增长；随着倾向悬露长度（工作面宽度）增大，厚硬岩层破断悬露长度呈现先增大后逐步减小的变化趋势。③营盘壕煤矿2201工作面推采过程中，厚硬岩层不会发生破断；当2202工作面推采至960 m左右时发生竖向“O-X”破断；随着工作面继续推进约188 m，厚硬岩层将发生周期性破断。④地表沉陷监测结果表明，2201工作面推采期间地表沉降值整体较小且无较大变化，以小能量微震事件为主；2202工作面推采期间地表下沉依次经历了缓慢下沉阶段、急剧下沉阶段、稳定阶段，大能量强矿震频率明显增大，大能量矿震发生位置与地表沉降最大值区域重合度较高，均处于“O-X”破断区域；地表下沉速度在距开切眼960 m处达到最大值9.87 mm/d，并诱发了“6·8”强矿震事件，验证了远场厚硬岩层破断规律的正确性。
Abstract:Mastering fracture and movement of far-field high-position hard-and-thick strata plays an important role in safety prevention and control of disasters including severe surface subsidence and strong mine seismic events. The fracture mechanical model of high-position hard-and-hick strata is established based on the panels 2201 and 2202 in Yingpanhao Coal Mine. The fracture and movement of the Cretaceous sandstone formation and its influencing factors are analyzed by using the theory of Vlasov thick plate, which is verified and analyzed by surface subsidence and microseismic events. The conclusions are as follows: ① In view of the occurrence characteristics of Cretaceous sandstone group that is far away from the coal seam, with large thickness and good integrity, a high-position hard-and-hick strata fracture mechanical model is established. And the critical mechanical conditions for the first fracture of high-position thick-and-hard rock stratum are calculated by Vlasov thick plate theory. ② With the increase of tensile strength, the fracture overhang length of hard-and-hick stratum slowly grow, linearly grow, and exponentially grow; As the thickness of the stratum increases, the fracture overhang length of the thick and hard rock stratum increases exponentially; With the increase of the overhang length along the dip (width of panel), the fracture overhang length of thick and hard rock stratum increases first and then decreases. ③ During the extraction of panel 2201 in Yingpanhao Coal Mine, the hard-and-hick stratum did not break; And when the panel 2202 advanced about 960 m, the vertical “O-X” fracture occured; When the panel continues to advance about 188 m, the hard-and-hick stratum breaks periodically. ④ The monitoring results of surface subsidence show that the surface subsidence value of panel 2201 is small as a whole, and there are many small energy micro-seismic events. The surface subsidence of panel 2202 has experienced slow subsidence, rapid subsidence and stable stages in turn, and the frequency of high-energy mine seismic event has increased significantly. The location of the high energy mine seismic events and the area of the maximum surface subsidence are highly coincident, both in the O-X break area; The surface subsidence velocity reached the maximum of the 9.87 mm/d at 960 m away from the setup room, inducing the “6·8” strong mine seismic event. The above phenomenons verified the correctness of the far-field thick and hard rock stratum fracturing behavior. The research results of this paper have guiding significance for the study on the fracture of thick and hard rock stratum and disaster pre-control under similar engineering geological conditions.
-
0. 引 言
由于形成于不同的地质历史时期，地层中不可避免地出现强度高、厚度大、整体性好的厚硬岩层，厚硬岩层是煤炭开采过程中较为常见的一种地质结构，在我国大同、兖州、新汶、鄂尔多斯、艾维尔沟等矿区均有分布[1-3]。特别是当厚硬岩层赋存高、远离采场时，其破断运动将影响覆岩大结构稳定性，甚至会诱发冲击地压、强矿震、煤与瓦斯突出等强烈动力灾害[4-7]。以我国鄂尔多斯地区为例，煤系地层中赋存有白垩系砂岩组，其强度高、厚度大、距离煤层远，在煤炭开采实践中，白垩系砂岩组破断将造成地表急剧下沉、大能量矿震频发的强烈矿压显现，甚至造成矿井停产停面，严重影响煤炭安全高效开采，因此，对远场高位厚硬岩层破断运动规律展开深入系统研究对于实现动力灾害防治及煤炭安全高效开采具有重要意义。
近年来，国内外学者对厚硬岩层破断运动规律进行了大量研究，取得了诸多有益成果。蒋金泉等[8]建立了厚硬岩层薄板力学模型，得到了岩层破断跨度表达公式，并利用微震、支架压力进行了岩层破断动力响应分析；姜福兴等[9]提出了覆岩运动“载荷三带”理论，并将其成功应用于冲击地压灾害预测预报及安全防控；朱卫兵等[10]采用了自制的大尺度三维物理模拟实验平台，研究了高位关键层“横U−Y”型破断特征及其运动规律；张明等[11-13]提出了厚硬岩层破断运动演化“台阶效应”，揭示了厚硬岩层破断型强矿震灾害评估方法和防控思路；王树立等[14]建立了多工作面联合开采条件下的侏罗系红层力学模型，分析了红层破断运动规律，并利用微震数据验证了其破断响应特征；刘一扬等[15]建立了厚硬岩层周期破断步距力学模型，并得到了周期破断步距计算公式，通过现场实测数据进行了验证；赵通等[16]建立了近距离赋存厚硬岩层破断的厚板模型，得到了其断裂失稳力学条件，并利用理论分析、数值模拟等方法进行了验证。上述成果为厚硬岩层破断力学规律研究提供了有益借鉴，但由于地层地质条件的复杂性，厚硬岩层物理力学特性及其在地层中的赋存层位存在显著差异，加之开采顺序与工艺方法造成的边界支承条件的区别，都将对厚硬岩层破断运动规律产生显著影响；且以往研究主要集中在中−低位厚硬岩层破断规律及其响应特征方面，对鄂尔多斯地区赋存的远场高位白垩系厚硬岩层在多工作面大空间开采条件下的破断机理及响应规律研究较少。
山东能源集团鄂尔多斯能化有限公司地区营盘壕煤矿2201、2202工作面为典型的高位厚硬白垩系砂岩赋存工作面，基于2201、2202工作面地质生产条件，利用符拉索夫厚板理论建立远场高位厚硬岩层的厚板力学模型，对远场高位厚硬岩层破断运动力学条件及其主要影响因素进行研究，进而揭示2201、2202工作面连续开采过程中高位厚硬岩层的破断演化过程，并通过地表沉陷、微震响应规律进行验证分析。本研究成果对于类似地层条件下动力灾害防治及煤炭安全高效开采具有重要指导意义。
1. 工程概况
营盘壕煤矿位于内蒙古自治区鄂尔多斯市西南部的乌审旗。井田南北长约13.63 km，东西宽约8.32 km，面积113.32 km2。矿井生产能力1 000万t/a，可采储量103 686万t。地面标高+1 244.6～+1 261.4 m，当前主采2-2煤层，煤层底板标高分别为+490～+540 m，平均埋深722.88 m，煤层厚度3.16~10.24 m，平均6.29 m，以暗煤为主，亮煤次之，半暗型煤为主，煤层普氏硬度为f=1.36。
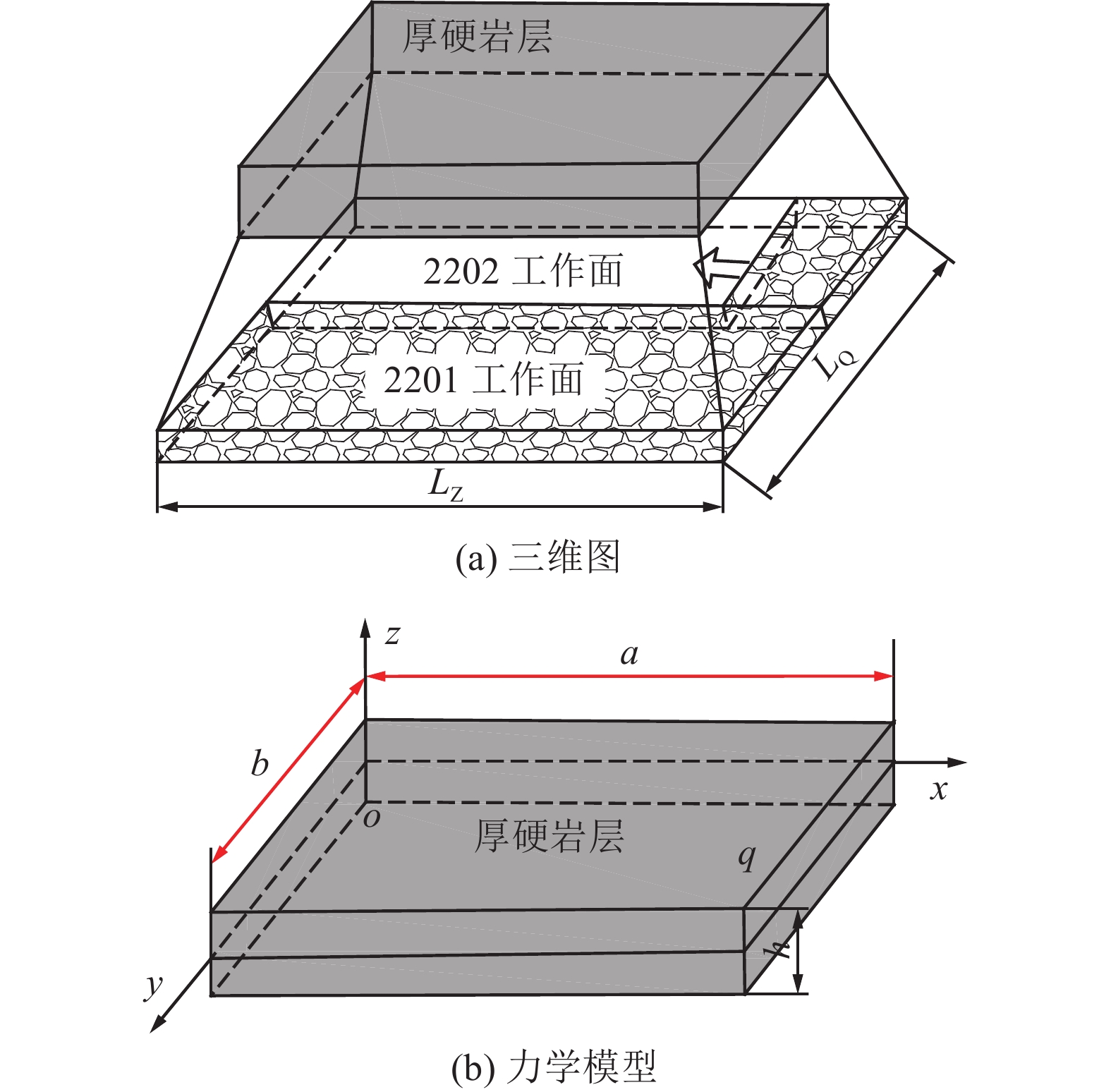
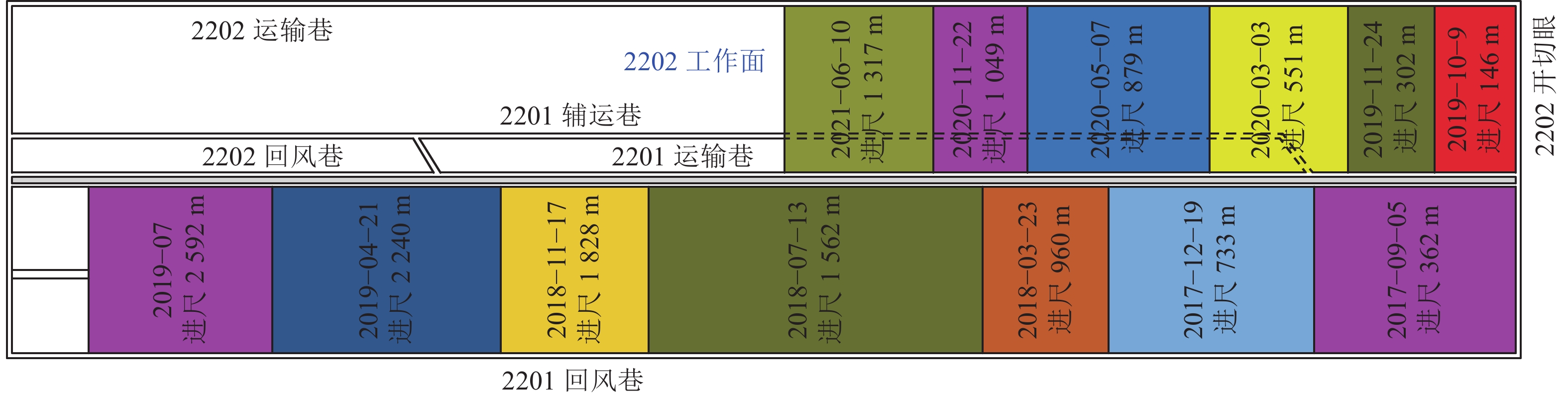
22采区为2-2煤层首采区，共布置6个工作面，2201工作面为首采工作面。主要研究对象为2201、2202工作面，两工作面倾向长度均为300 m、走向长度均为2709 m；2201工作面于2017年3月开始回采至2019年7月回采结束；2202工作面于2019年8月开始回采，目前已回采1317.8 m左右，如图1所示。
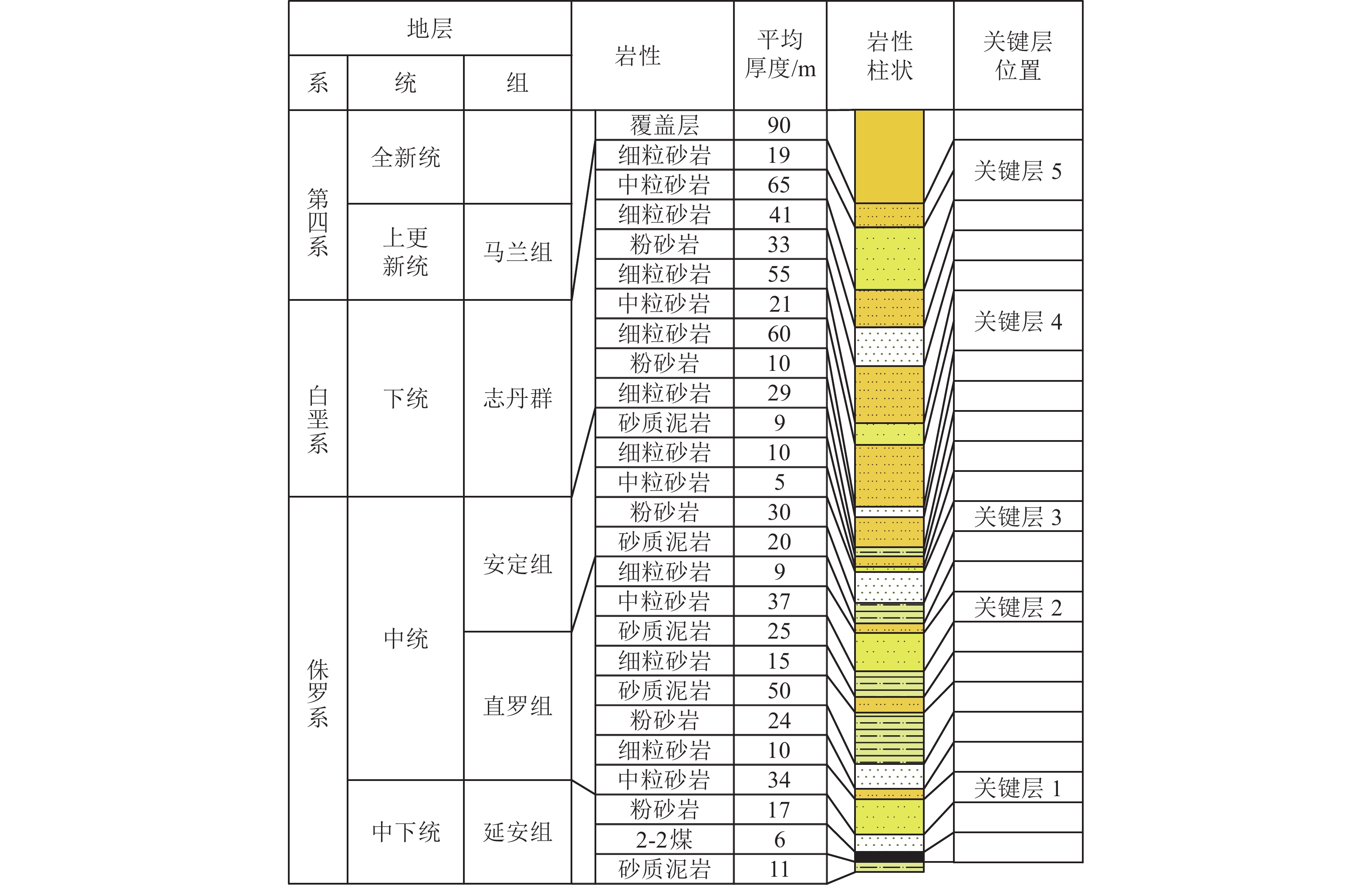
图2为2202工作面K7-7钻孔柱状图。通过关键层理论计算可知，2202工作面顶板含有多层关键层组，其中白垩系内主要有关键层4、5两层关键层组，其均具有厚度大、强度高、整体性强、距离煤层远的特点。由矿山岩层运动理论可知，煤炭开采过程中，随着开采面积的不断增大，采空区上覆岩层不断发生垮落，离层裂隙逐步向上发展并止于高位厚硬岩层底部[17]；随着开采面积不断增大，离层空间逐渐增大，厚硬岩层逐渐悬露，当达到破断极限时，厚硬岩层破断将对采场覆岩运动造成影响，甚至会产生地表强烈沉降、大能量矿震等事件，威胁矿井安全高效生产。由此推知，对于营盘壕22采区而言，侏罗系白垩系砂岩破断运动将对下部煤炭安全高效开采产生重要影响，开展针对性研究极具必要性和紧迫性。
2. 厚硬岩层板结构模型及破断解析
由于白垩系岩层厚度大、距采场远、强度高，其初次破断前悬露面积大，采用梁理论计算求解破断规律会产生较大偏差，因此，采用符拉索夫厚板理论[18]建立厚硬岩层空间结构力学模型并进行破断规律分析。需要说明的是，由于当前开采阶段采空区范围不足够大，主要以白垩系内关键层4破断运动为主，故研究的厚硬岩层主要是关键层4，其厚度为81 m，距离煤层334 m，如图2所示。
2.1 厚硬岩层板结构力学模型构建
由板结构理论[19-21]可知，当岩层厚度与破断面最小特征尺寸之比小于1/5时，可用弹性薄板的相关理论求解，但当岩层厚度与破断面最小特征尺寸之比大于1/5时，应采用厚板的相关理论求解，据此，可将厚硬岩层破断问题视为厚板结构问题处理。同时2201、2202工作面四周无明显切割断层，由此可以认为，初次破断前厚硬岩层四周嵌固在岩体内并受到下部岩层的支承，形成四周固支的边界状态。并进行如下假设[18]：①厚硬岩层破断前属于弹性变形范畴，符合胡克定律；②厚硬岩层裂隙少，可认为是连续的，符合连续性假设；③厚硬岩层变形前垂直于中面的直线，变形后弯曲成抛物线；④厚硬岩层处于广义平面应力状态并忽略横向应变的影响；⑤厚硬岩层的挠度、应力沿平板厚度方向呈线性规律分布。
基于上述假设条件，以厚硬岩层的中面为基准面，建立四周固支的厚板力学模型，如图3所示。其中：x轴是工作面走向推进方向；y轴是工作面倾斜方向；z轴是垂直方向；原点O位于厚板中面三轴交汇处；h为厚硬岩层厚度；a为岩层破断时的走向悬露长度；b为岩层破断时的倾向悬露长度；q（x，y）为厚硬岩层所受均布载荷；H为厚硬岩层与煤层间距；LZ和LQ为破断时工作面沿走向和倾向的推进长度。
![]()
图 3 远场高位厚硬岩层厚板力学模型Figure 3. Thick-plate mechanical model of super-high position hard-and-hick strata2.2 厚硬岩层初次破断力学解析
考虑到厚硬岩层赋存条件和弯曲运动复杂性，采用简化的符拉索夫理论[22]进行求解。
基于符拉索夫理论得到厚板弯曲微分方程组：
$${ \begin{gathered} {\nabla ^2}{\psi _{{x}}} + \frac{{1 + \nu }}{2}\frac{\partial }{{\partial y}}\left( {\frac{{\partial {\psi _{{y}}}}}{{\partial x}} - \frac{{\partial {\psi _{{x}}}}}{{\partial y}}} \right) + \frac{1}{4}\frac{\partial }{{\partial x}}\left( {{\nabla ^2}\omega } \right) = \frac{{5Gh}}{{6D}}\left( {{\psi _{{x}}} - \frac{{\partial \omega }}{{\partial x}}} \right) \\ {\nabla ^2}{\psi _{{y}}} + \frac{{1 + \nu }}{2}\frac{\partial }{{\partial x}}\left( {\frac{{\partial {\psi _x}}}{{\partial y}} - \frac{{\partial {\psi _y}}}{{\partial x}}} \right) + \frac{1}{4}\frac{\partial }{{\partial y}}\left( {{\nabla ^2}\omega } \right) = \frac{{5Gh}}{{6D}}\left( {{\psi _y} - \frac{{\partial \omega }}{{\partial y}}} \right) \\ \frac{{\partial {\psi _x}}}{{\partial x}} + \frac{{\partial {\psi _y}}}{{\partial y}} - {\nabla ^2}\omega = \frac{3}{{2Gh}}q\left( {x,y} \right) \\ \end{gathered}} $$ (1) 式中：D为抗弯刚度；E为弹性模量；h为岩层厚度；Ψx，Ψy分别为x，y的转角；ν为泊松比；ω为挠度；G为剪切变形模量；q为均布载荷。
四周固支板结构的边界条件如下：
$$ \begin{gathered} \omega \left| {_{x = 0,x = a}} \right. = 0,{\psi _y}\left| {_{x = 0,x = a}} \right. = 0,{M_y}\left| {_{x = 0,x = a}} \right. = 0 \\ \omega \left| {_{y = 0,y = b}} \right. = 0,{\psi _x}\left| {_{y = 0,y = b}} \right. = 0,{M_y}\left| {_{y = 0,y = b}} \right. = 0 \\ \end{gathered} $$ (2) 利用式（2），可得内力、内力矩表达式：
$$ \begin{gathered} {M_x} = - \frac{D}{5}\left[ {4\left( {\frac{{\partial {\psi _x}}}{{\partial x}} + \nu \frac{{\partial {\psi _y}}}{{\partial y}}} \right) + \left( {\frac{{{\partial ^2}\omega }}{{\partial {x^2}}} + \nu \frac{{{\partial ^2}\omega }}{{\partial {y^2}}}} \right)} \right] \\ {M_y} = - \frac{D}{5}\left[ {4\left( {\frac{{\partial {\psi _y}}}{{\partial y}} + \nu \frac{{\partial {\psi _x}}}{{\partial x}}} \right) + \left( {\frac{{{\partial ^2}\omega }}{{\partial {y^2}}} + \nu \frac{{{\partial ^2}\omega }}{{\partial {x^2}}}} \right)} \right] \\ {M_{xy}} = - \frac{{D\left( {1 - \nu } \right)}}{5}\left[ {2\left( {\frac{{\partial {\psi _x}}}{{\partial y}} + \frac{{\partial {\psi _y}}}{{\partial x}}} \right) + \frac{{{\partial ^2}\omega }}{{\partial x\partial y}}} \right] \\ {Q_x} = \frac{2}{3}Gh\left( {\frac{{\partial \omega }}{{\partial x}} - {\psi _x}} \right),{Q_y} = \frac{2}{3}Gh\left( {\frac{{\partial \omega }}{{\partial y}} - {\psi _y}} \right) \\ \end{gathered} $$ (3) 微分平衡方程可写为
$$ \begin{gathered} \frac{{2D}}{5}\left[ {\left( {1 - \nu } \right){\nabla ^2}{\psi _x} + \left( {1 + \nu } \right)\frac{{\partial \Phi }}{{\partial x}} + \frac{1}{2}\frac{\partial }{{\partial x}}\left( {{\nabla ^2}\omega } \right)} \right] + \\ \frac{2}{3}Gh\left( {\frac{{\partial \omega }}{{\partial x}} - {\psi _x}} \right) = 0 \\ \frac{{2D}}{5}\left[ {\left( {1 - \nu } \right){\nabla ^2}{\psi _y} + \left( {1 + \nu } \right)\frac{{\partial \Phi }}{{\partial y}} + \frac{1}{2}\frac{\partial }{{\partial y}}\left( {{\nabla ^2}\omega } \right)} \right] +\\ \frac{2}{3}Gh\left( {\frac{{\partial \omega }}{{\partial y}} - {\psi _y}} \right) = 0 \\ \frac{2}{3}Gh\left( {{\nabla ^2}\omega - \Phi } \right) + q\left( {x,y} \right) = 0 \\ \Phi = \frac{{\partial {\psi _x}}}{{\partial x}} + \frac{{\partial {\psi _y}}}{{\partial y}} \\ \end{gathered} $$ (4) 设挠度、转角函数分别为
$$ \begin{gathered} \omega = \sum\limits_{m = 1}^\infty {\sum\limits_{n = 1}^\infty {{A_{mn}}} } \sin \frac{{m\pi x}}{a}\sin \frac{{n\pi y}}{b} \\ {\psi _x} = \sum\limits_{m = 1}^\infty {\sum\limits_{n = 1}^\infty {{B_{mn}}} } \cos \frac{{m\pi x}}{a}\sin \frac{{n\pi y}}{b} \\ {\psi _y} = \sum\limits_{m = 1}^\infty {\sum\limits_{n = 1}^\infty {{C_{mn}}} } \sin \frac{{m\pi x}}{a}\cos \frac{{n\pi y}}{b} \\ \end{gathered} $$ (5) 同时将载荷也展成双三角级数：
$$ q(x,y) = \sum\limits_{m = 1}^\infty {\sum\limits_{n = 1}^\infty {{q_{mn}}} } \sin \frac{{m\pi x}}{a}\sin \frac{{n\pi y}}{b} $$ (6) 将（5）、（6）代入（3）中，得：
$$ \begin{gathered} {A_{mn}} = \left\{ {1 + \dfrac{{6D{\pi ^2}}}{{5Gh}}\left[ {{{\left( {\dfrac{m}{a}} \right)}^2} + {{\left( {\dfrac{n}{b}} \right)}^2}} \right]} \right\}\dfrac{{{q_{mn}}}}{{D{\pi ^4}{{\left[ {{{\left( {\dfrac{m}{a}} \right)}^2} + {{\left( {\dfrac{n}{b}} \right)}^2}} \right]}^2}}} \\ {B_{mn}} = \left\{ {1 - \dfrac{{3D{\pi ^2}}}{{10Gh}}\left[ {{{\left( {\dfrac{m}{a}} \right)}^2} + {{\left( {\dfrac{n}{b}} \right)}^2}} \right]} \right\}\dfrac{{m{q_{mn}}}}{{aD{\pi ^3}{{\left[ {{{\left( {\dfrac{m}{a}} \right)}^2} + {{\left( {\dfrac{n}{b}} \right)}^2}} \right]}^2}}} \\ {C_{mn}} = \left\{ {1 - \dfrac{{3D{\pi ^2}}}{{10Gh}}\left[ {{{\left( {\dfrac{m}{a}} \right)}^2} + {{\left( {\dfrac{n}{b}} \right)}^2}} \right]} \right\}\dfrac{{n{q_{mn}}}}{{aD{\pi ^3}{{\left[ {{{\left( {\dfrac{m}{a}} \right)}^2} + {{\left( {\dfrac{n}{b}} \right)}^2}} \right]}^2}}} \\ \end{gathered} $$ (7) 将Amn、Bmn、Cmn方程组级数展开到一级（m=n=1），得到：
$$ \begin{gathered} {A_{11}} = \left[ {1 + \dfrac{{6D{\pi ^2}}}{{5Gh}}\left( {\dfrac{1}{{{a^2}}} + \dfrac{1}{{{b^2}}}} \right)} \right] \dfrac{{{q_{11}}}}{{D{{\text{π}} ^4}{{\left( {\dfrac{1}{{{a^2}}} + \dfrac{1}{{{b^2}}}} \right)}^2}}} \\ {B_{11}} = {C_{11}} = \left[ {1 - \dfrac{{3D{\pi ^2}}}{{10Gh}}\left( {\dfrac{1}{{{a^2}}} + \dfrac{1}{{{b^2}}}} \right)} \right] \dfrac{{{q_{11}}}}{{aD{{\text{π}} ^3}{{\left( {\dfrac{1}{{{a^2}}} + \dfrac{1}{{{b^2}}}} \right)}^2}}} \\ \end{gathered} $$ (8) 将（5）、（6）、（8）代入（3）中，得Mx，My：
$$ \begin{gathered} {M_x} = \dfrac{D}{5}\left[ {\dfrac{{{q_{11}}\left( {\dfrac{5}{{{a^2}}} + \dfrac{{4\nu }}{{ab}} + \dfrac{\nu }{{{b^2}}}} \right)}}{{D{{\text{π}} ^2}{{\left( {\dfrac{1}{{{a^2}}} + \dfrac{1}{{{b^2}}}} \right)}^2}}} + \dfrac{{6{q_{11}}\nu \left( {\dfrac{1}{{{b^2}}} - \dfrac{1}{{ab}}} \right)}}{{5Gh\left( {\dfrac{1}{{{a^2}}} + \dfrac{1}{{{b^2}}}} \right)}}} \right] \times \\ \qquad\qquad\qquad\sin \dfrac{{\pi x}}{a} \times \sin \dfrac{{\pi y}}{b} \\ {M_y} = \dfrac{D}{5}\left[ {\dfrac{{{q_{11}}\left( {\dfrac{5}{{{a^2}}} + \dfrac{{4\nu }}{{ab}} + \dfrac{\nu }{{{b^2}}}} \right)}}{{D{{\text{π}} ^2}{{\left( {\dfrac{1}{{{a^2}}} + \dfrac{1}{{{b^2}}}} \right)}^2}}} + \dfrac{{6{q_{11}}\nu \left( {\dfrac{1}{{{a^2}}} - \dfrac{1}{{ab}}} \right)}}{{5Gh\left( {\dfrac{1}{{{a^2}}} + \dfrac{1}{{{b^2}}}} \right)}}} \right] \times \\ \qquad\qquad\qquad\sin \dfrac{{\pi x}}{a} \times \sin \dfrac{{\pi y}}{b} \\ \end{gathered} $$ (9) 由于Mx=My，则在x=a/2，y=b/2时，弯矩取得最大值，可令Mmax=Mxmax得：
$$ {M_{\max }} = {M_{x\max }} = \dfrac{D}{5}\left[ {\dfrac{{{q_{11}}\left( {\dfrac{5}{{{a^2}}} + \dfrac{{4\nu }}{{ab}} + \dfrac{\nu }{{{b^2}}}} \right)}}{{D{{\text{π}} ^2}{{\left( {\dfrac{1}{{{a^2}}} + \dfrac{1}{{{b^2}}}} \right)}^2}}} + \dfrac{{6{q_{11}}\nu \left( {\dfrac{1}{{{b^2}}} - \dfrac{1}{{ab}}} \right)}}{{5Gh\left( {\dfrac{1}{{{a^2}}} + \dfrac{1}{{{b^2}}}} \right)}}} \right] $$ (10) 厚板下表面最大拉应力为
$$ {\sigma _{\max }} = \frac{{12{M_{\max }}}}{{{h^3}}}Z = \frac{{12{M_{\max }}}}{{{h^3}}} \times \frac{h}{2} = \frac{{6{M_{\max }}}}{{{h^2}}} $$ (11) 考虑到厚硬岩层抗拉强度最小，其破坏形式主要为拉断破坏，当厚板下表面应力σmax超过其抗拉强度σs时，厚板将发生张拉破坏，由此可以得到厚板发生破断的临界力学条件为
$$ {\sigma _{\max }} = {\sigma _{\rm{s}}} = \dfrac{{6{q_{11}}\left( {\dfrac{5}{{{a^2}}} + \dfrac{{4\nu }}{{ab}} + \dfrac{\nu }{{{b^2}}}} \right)}}{{5{{\text{π}} ^2}{{\left( {\dfrac{1}{{{a^2}}} + \dfrac{1}{{{b^2}}}} \right)}^2}{h^2}}} + \dfrac{{6{q_{11}}\nu \left( {\dfrac{1}{{{b^2}}} - \dfrac{1}{{ab}}} \right)}}{{25\left( {1 - \nu } \right)\left( {\dfrac{1}{{{a^2}}} + \dfrac{1}{{{b^2}}}} \right)}} $$ (12) 由式（12）可知，远场高位厚硬岩层破断尺寸特征将受岩石抗拉强度σs、岩层厚度h、上覆载荷q、泊松比υ等因素的影响。
当厚板无限长时（b=+∞），可得厚板的极限破断步距：
$$ a ={\text{π}} h\sqrt {\frac{{[{\sigma _{\rm{s}}}]}}{{6q}}} $$ (13) 当a=b时，厚硬岩层发生正“O-X”破断，可得破断步距为
$$ a = {\text{π}} h\sqrt {\frac{{2{\sigma _{\rm{s}}}}}{{3q(1 + \upsilon )}}} $$ (14) 考虑到岩层破裂角影响，厚硬岩层破断尺寸与开采空间尺寸对应关系如下：
$$ \begin{gathered} {L_{\text{Z}}} = a + 2H\cot \;\alpha \\ {L_{\text{Q}}} = b + 2H\cot \;\alpha \\ \end{gathered} $$ (15) 式中：α为岩层破断角；LZ为厚板模型在工作面沿走向方向长度；LQ为厚板模型在工作面沿倾向方向长度。
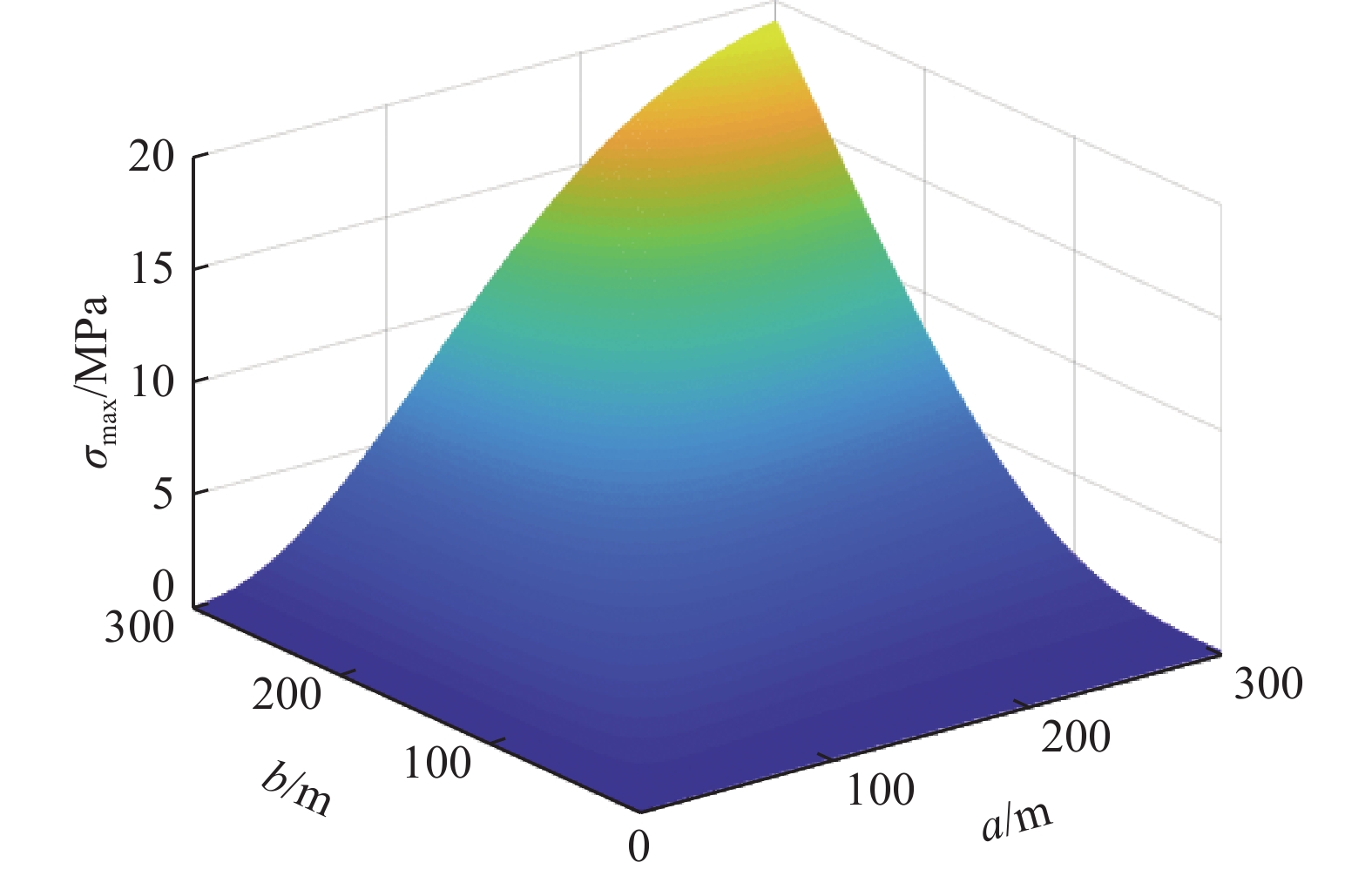
结合具体工程地质条件，厚硬岩层发生破断时沿走向悬露长度a和倾向悬露长度b可分别由式（12）—式（14）得到，进而可由式（15）计算得相应的开采空间走向和倾向尺度LZ和LQ。图4为某一具体条件下厚硬岩层破断时悬露长度（a、b）与极限破断应力的关系变化。分析可知，在理想条件下，只有沿走向和倾向的悬露尺寸均达到了破断极限，厚硬岩层才会发生破断；但在实际工程实践中，工作面走向推进长度要远大于倾向长度；单工作面开采下，即便走向推进距离达到了破断极限，但若倾斜长度小于破断极限，此时厚硬岩层可视为稳定的无限长梁，不会发生破断，需要多个工作面联合开采，使开采空间倾斜方向长度亦达到破断极限，厚硬岩层才会发生破断。
![]()
图 4 岩层破断尺寸（a、b）与岩层抗拉强度σmax关系变化Figure 4. Fracture size (a, b) and tensile strength of rock stratum σmax relation change3. 厚硬岩层初次破断影响因素分析
为进一步研究高位厚硬岩层初次破断的主要影响因素，岩石抗拉强度取值参考文献[14,19-21]，取σs=4.68 MPa，q=10 MPa，υ=0.3，建立如下极限状态函数：
$$ f(\sigma _{{\rm{s}}}、h、b、q、\upsilon )=(4.68、81、289、10、0.3)$$ (16) 依据式(12)、式(14)，固定其他参数，每次仅改变单一参数,采用单因素分析法研究各因素对走向悬露长度a的影响规律。
3.1 抗拉强度
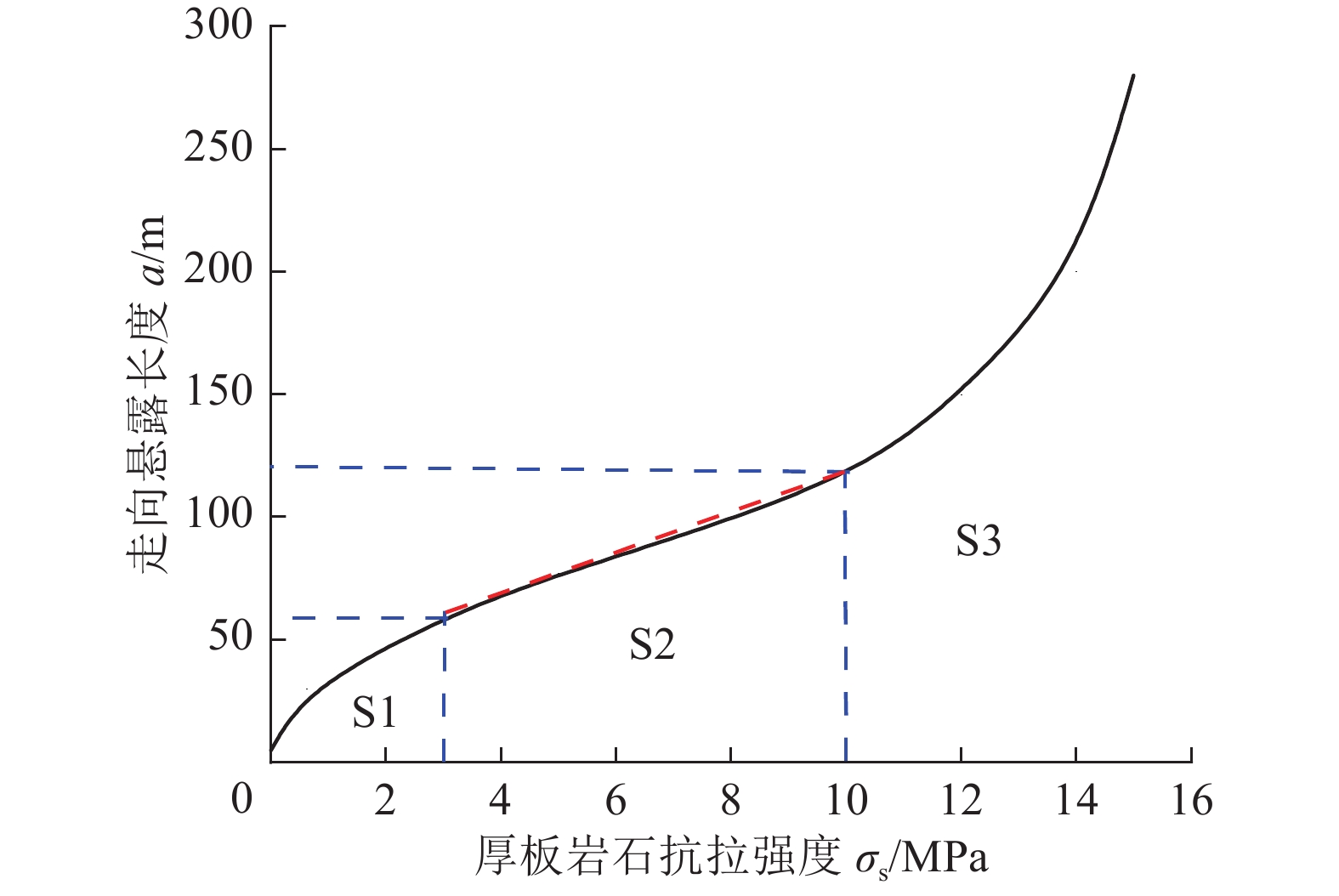
图5为厚板岩石抗拉强度σs与走向悬露长度a的影响关系。由图5可知，厚硬岩层走向悬露长度a随着抗拉强度σs的增大呈现明显阶段性特征：①当抗拉强度σs≤3 MPa时（S1阶段），随着抗拉强度增大，岩层走向悬露长度逐渐增大，但增长速率逐渐降低；②当抗拉强度3 MPa≤σs≤10 MPa时（S2阶段），随着抗拉强度增大，岩层走向悬露长度近似呈线性增大趋势，增长速率近似保持固定值；③当抗拉强度 σs≥10 MPa时（S3阶段），岩体抗拉强度对岩层破断尺寸的影响作用尤为突出，随着抗拉强度增大，走向悬露长度近似呈指数型增长，此阶段，由于岩体抗拉强度极高，岩体整体性强，岩层发生破断难度急速增大，需要更大的开采空间才能提高增大岩层下表面受到的拉应力。
![]()
图 5 岩石抗拉强度σs与走向悬露长度a关系Figure 5. Relationship between rock tensile strength σs and strike overhang length a3.2 岩层厚度
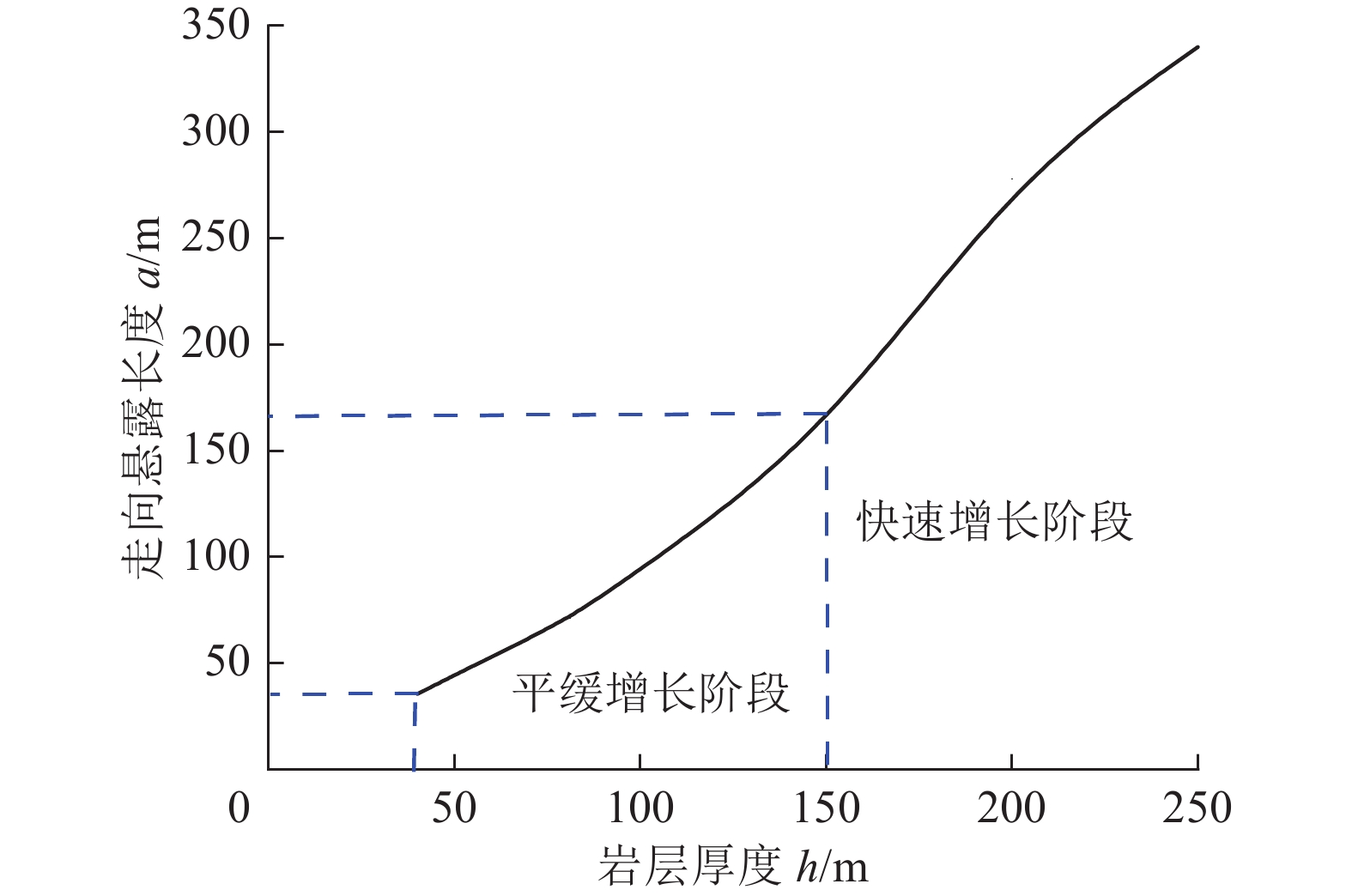
图6为岩层厚度h与走向悬露长度ɑ的影响关系。由图6可知，远场高位厚硬岩层走向悬露长度a随岩层厚度h的增大近似呈现指数型增长。这是由于岩层厚度越大，相应岩层强度越高，其发生整体破断所需要的下部离层空间越大，相应的岩层悬露长度亦越大。需要说明的是，图6是依据符拉索夫厚板研究所得，在岩层厚度小于40 m时，岩层厚度过小，岩层属于薄板范围，不能应用厚板理论研究，故该阶段无数据。
![]()
图 6 岩层厚度h与走向悬露长度a关系Figure 6. Relation between thickness of strata h and strike overhang length a3.3 倾向悬露长度
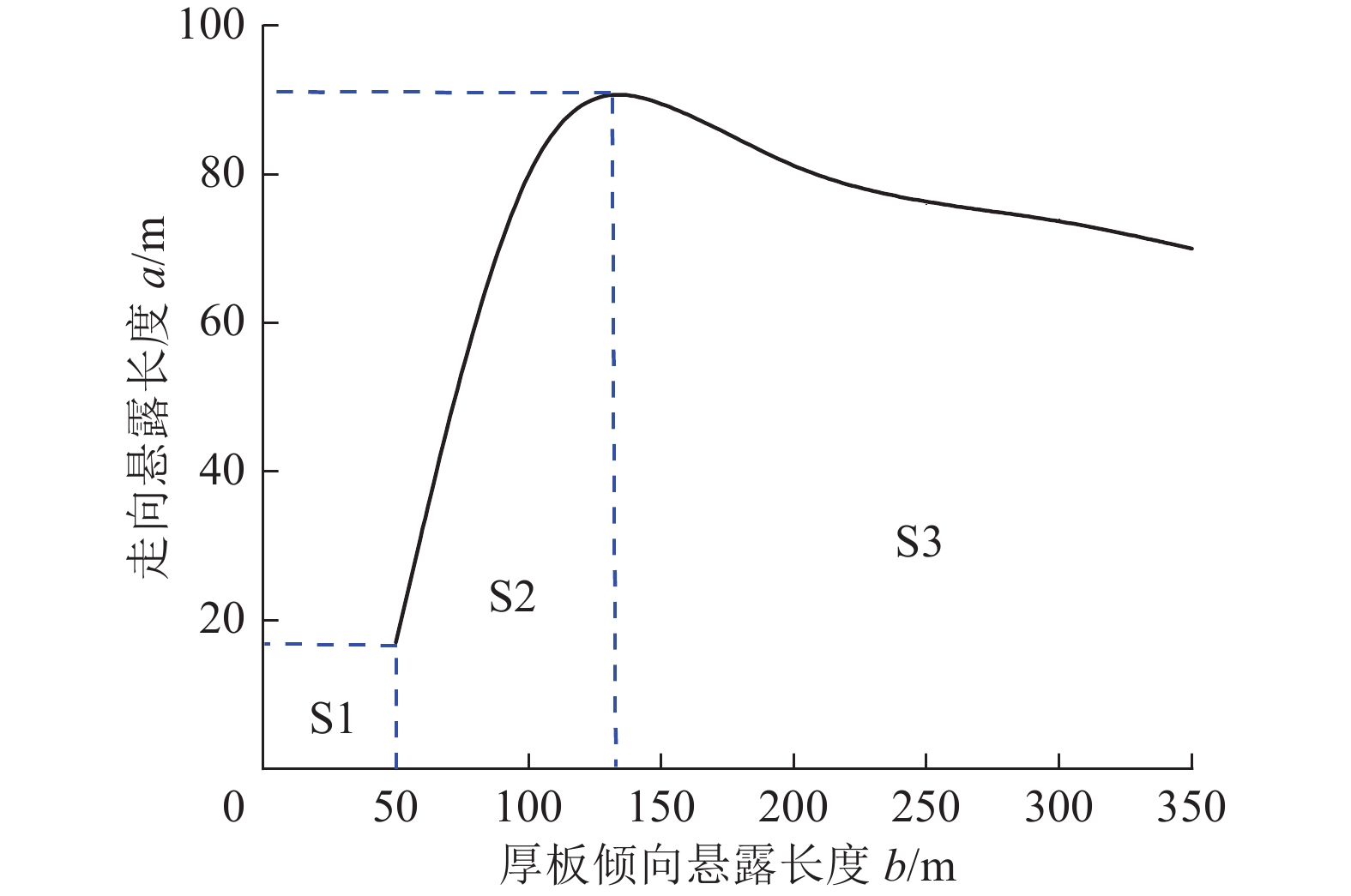
式（15）给出了厚硬岩层倾向悬露长度与工作面倾向长度存在对应关系；结合实际工程开采条件，单个工作面倾向宽度为固定值，开采过程中相应的厚硬岩层倾向悬露长度b亦为固定值，因此，通过分析倾向悬露长度b与走向悬露长度a的关系，可间接分析工作面倾向宽度对厚硬岩层破断尺寸的影响。图7为厚板倾向悬露长度b与走向悬露长度a的影响关系。由图7分析可知，厚硬岩层走向悬露长度a随倾向悬露长度b增大，呈先增大后逐步减小的变化趋势，总体可划分为：稳定阶段、快速增长阶段、缓慢减小阶段：①当倾向悬露长度b<50 m时（S1阶段），由于厚硬岩层悬顶面积过小，相应的岩层下表面拉应力小、且远小于岩层抗拉极限，此阶段岩层无法发生破断，处于稳定状态，故而无相应数据。②当倾向悬露长度50 m<b<130 m时（S2阶段），随着倾向悬露长度b增大，走向悬露长度a近似呈线性增长，此阶段厚硬岩层处于非充分运动阶段，悬露长度的变化直接影响厚硬岩层拉应力状态。③当倾向悬露长度b>130 m时（S3阶段），随着倾向悬露长度b的增大，走向悬露长度a近似呈幂函数式减小，这是由于工作面倾向长度达到一定值后继续增大，厚硬岩层处于充分采动阶段，边界对厚硬岩层应力状态的影响能力下降，减小了对厚硬岩层初次破断和运动的限制，导致厚硬岩层破断步距减小。
![]()
图 7 倾向悬露长度b与走向悬露长度a关系Figure 7. Relation between inclination overhang length b and strike overhang length a4. 远场厚硬关键层破断演化力学过程
根据营盘壕煤矿具体工程地质条件及矿方提供数据可知，σs=4.68 MPa，υ=0.3，α=65°，h=81 m，关键层上覆岩层厚度为384 m、相应载荷q取10 000 kN/m2。将相关参数代入式（12）、式（13）进行分析计算，可分析得到厚硬岩层的极限破断步距为71 m，当a=b=125 m时发生正“O-X”破断。
由关键层理论可知，关键层发生破断需要满足2个条件：关键层下部有离层空间，且悬露距离达到岩层极限破断步距。
1）2201工作面回采期间，LQ=300 m，LZ=2704 m，可以认为走向长度无穷大；此阶段内，工作面开采引起的最大覆岩破坏高度约为采空区短边长度的1/2[22]，约150 m，未能波及到白垩系厚硬砂岩，主要是关键层1、2发生破断运动，关键层3、4保持较好稳定性；由式（15）亦可知，LQ=300 m时，b<71 m，未达到极限破断步距。因此，2201工作面开采期间厚硬岩层不会发生破断。
2）2202工作面回采期间，随着工作面推进，覆岩破裂高度不断增大，当推采至双见方阶段时，覆岩破裂高度达到最大值，约300 m，此时覆岩运动开始波及到白垩系厚硬岩层，关键层4下部开始出现离层空间，开始悬顶；此阶段内2201、2202两个工作面倾向长度LQ=600 m，相应的关键层倾向悬露长度b=289 m＞71 m，满足破断要求；自厚硬岩层开始悬顶、工作面往前继续推进382 m，相应的厚硬岩层走向悬露长度达到71 m，将会发生破断。厚硬岩层发生破断时的悬露长度b=289 m＞a=71 m，由此判定岩层将发生竖向“O-X”破断。
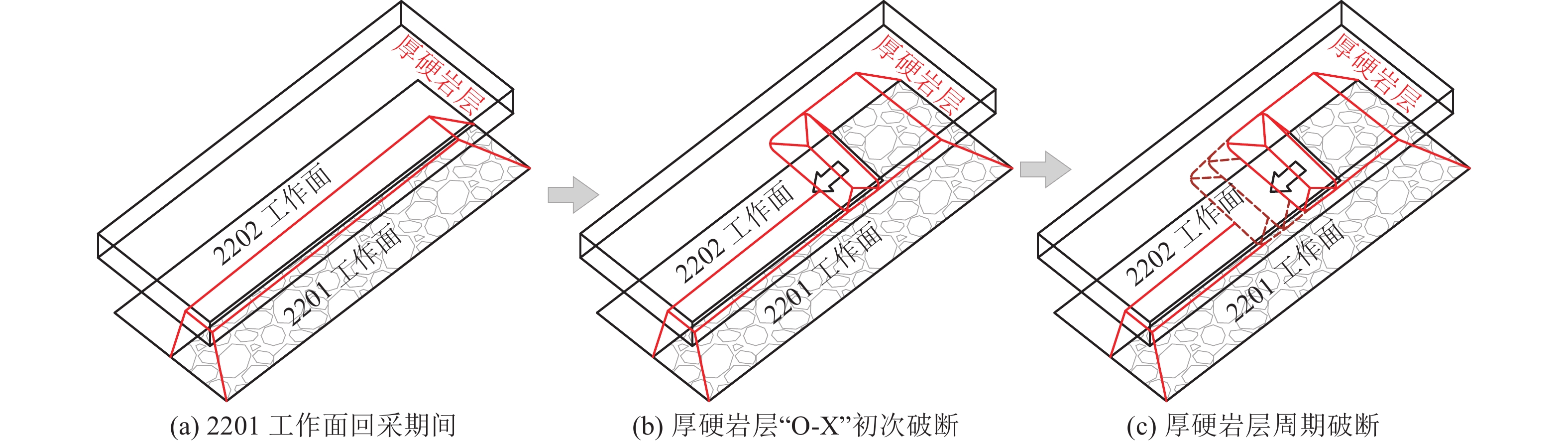
3）关键层发生初次破断后，随着2202工作面继续推进，厚硬岩层将会发生周期性破断，可按照“悬臂梁”结构计算，得出关键层4周期破断步距为32 m，即工作面至少推进约188 m时，关键层4发生周期破断，依次循环，直至工作面推采结束，如图8所示。
![]()
图 8 高位厚硬岩层破断力学过程Figure 8. Fracture mechanics process of high position hard-and-hick strata5. 远场厚硬岩层破断响应规律分析
5.1 地表沉陷响应规律
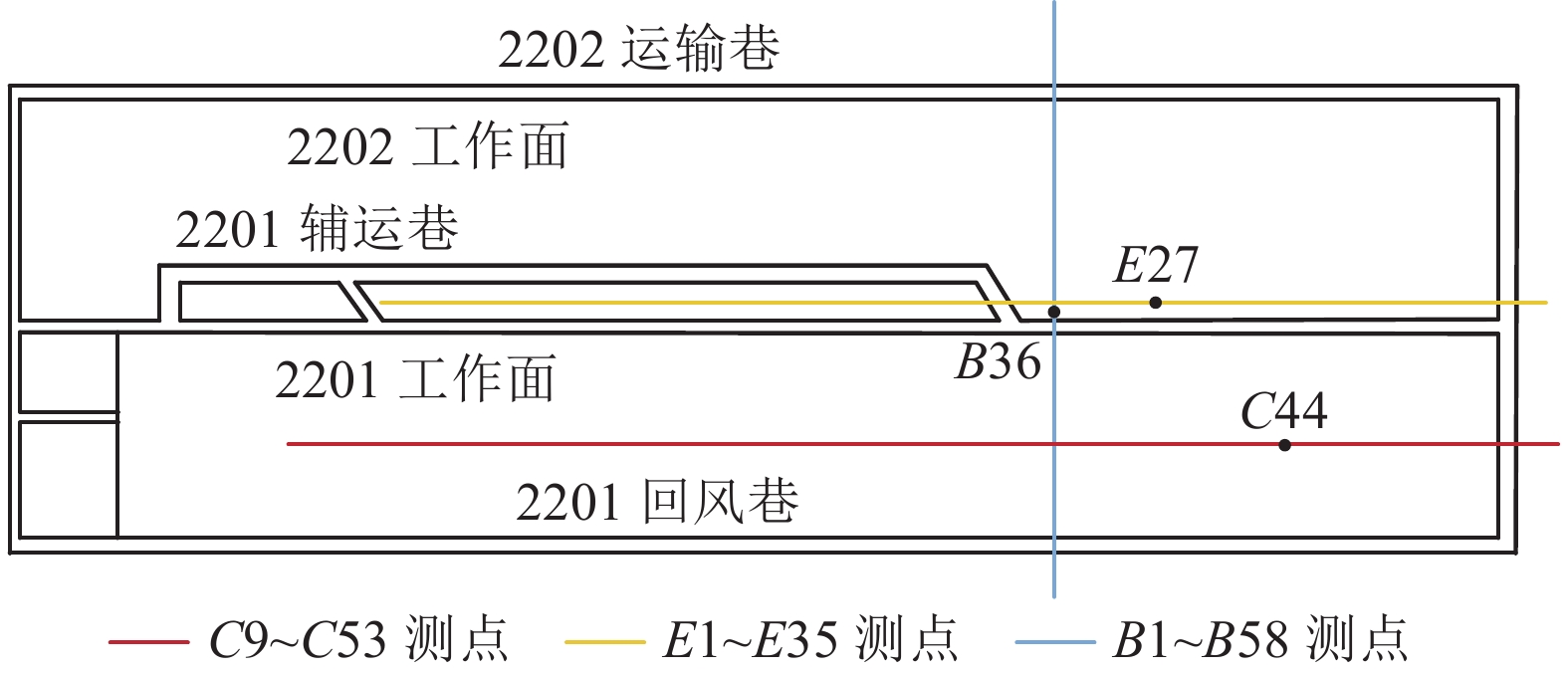
为验证上述厚硬岩层破断演化过程的正确性，对工作面推采过程中地表沉降规律进行监测，分析厚硬岩层破断演化诱发的地表响应特征。2201、2202工作面推采过程中，代表性地表岩移观测线（B、C、E测线），如图9所示。
2201工作面推采过程中的地表沉陷数据表明，2201工作面推采期间地表沉降值整体较小且无较大变化，最大值仅为339 mm，地表下沉系数η=0.057，表明2201工作面开采过程中覆岩未充分运动，白垩系砂岩未能发生破断；因此，主要对2202工作面推采期间地表沉陷规律进行监测与分析。2202工作面自2019年8月开始回采，至2021年6月时，工作面已经回采1 317.8 m，在此期间对地表沉陷规律进行监测，并在岩层剧烈活动期间增加监测次数，以便获得详尽地表沉降变化规律，绘制2202工作面回采期间各个测线地表下沉量曲线图，如图10—图12所示。
![]()
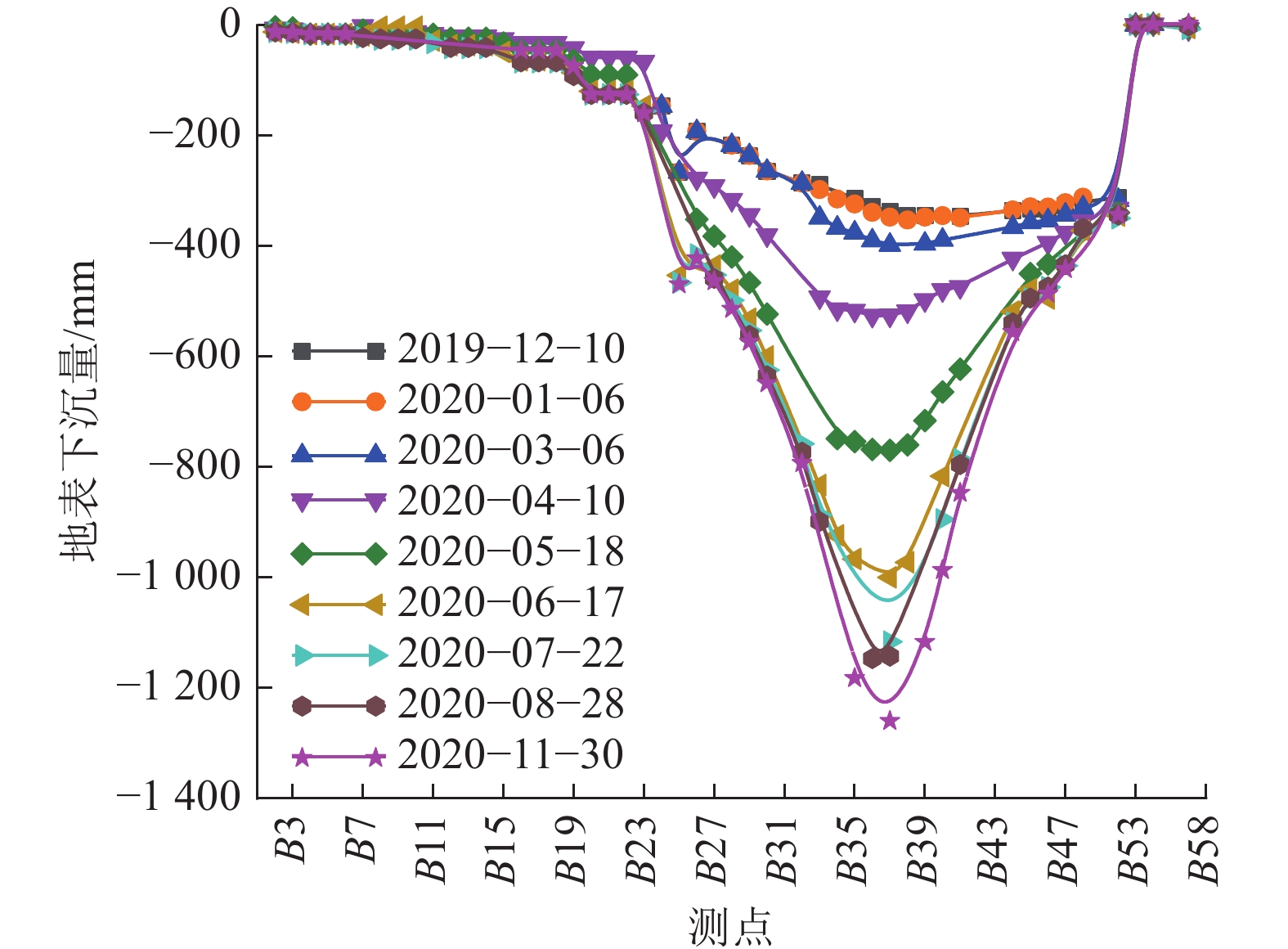
图 10 2202工作面倾向线B1～B58测点地表下沉统计Figure 10. Statistical of surface subsidence at monitoring points B1～B58 of inclination line of panal 2202图10为沿工作面倾向测点B1~B58的地表下沉数据。由图可知，地表最大下沉值均出现在B36号测点附近，2020年11月30日监测到最大下沉量1 260 mm，地表下沉系数η=0.21；该变化趋势表明：在工作面倾向方向地表下沉系数较小，地表在持续下降，岩层未充分沉降。
![]()
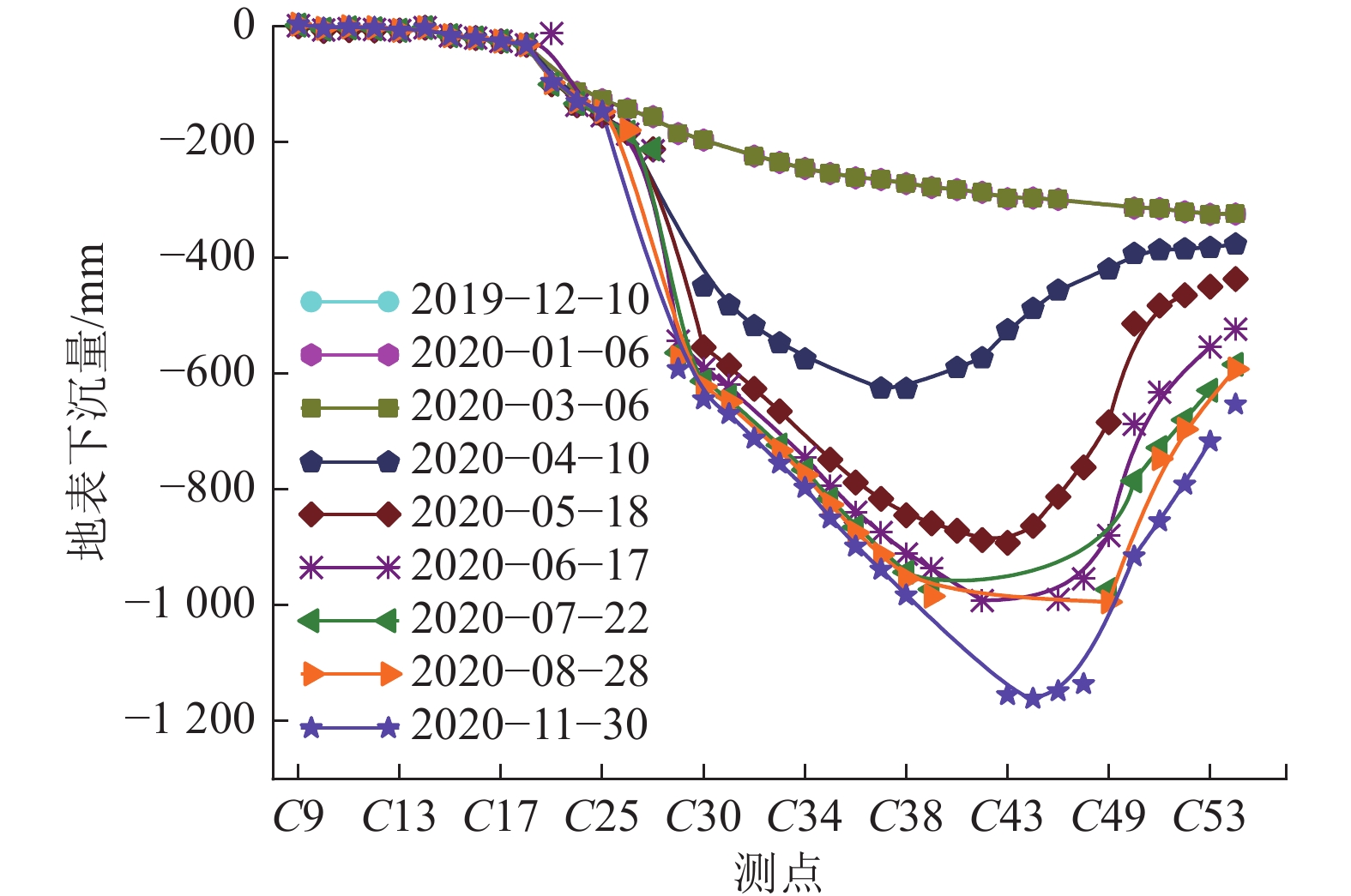
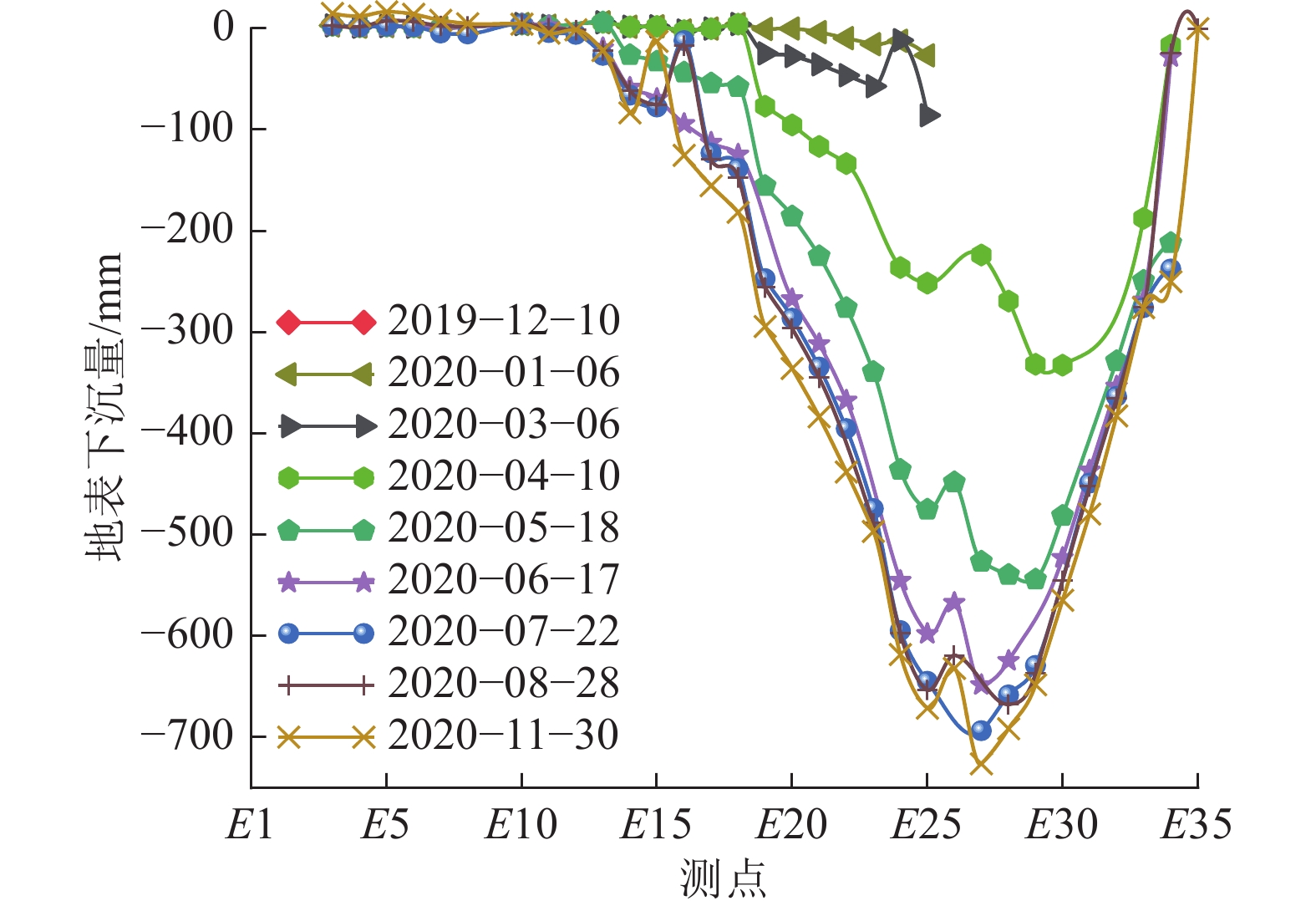
图 12 2202工作面走向线C9～C53测点地表下沉统计Figure 12. Statistical of surface subsidence at measuring points C9～C53 of strike line of panal 2202 face图11为沿工作面走向测点E1~E35的地表下沉数据。由图11可知，地表最大下沉值均出现在E27测点附近，2020年11月30日监测到最大下沉量726 mm，地表下沉系数η=0.121。图12为沿工作面走向测点C9～C53地表下沉量，最大下沉值均出现在C44测点附近，2020年11月30日监测到最大下沉量1 162 mm，地表下沉系数η=0.194。由图11、图12可知，在工作面走向方向地表下沉系数较小，地表在持续下降，岩层未充分沉降；同时对比图11、图12可知，E测线地表下沉量小于C测线地表下沉值，这是由于测线C靠近2201采空区造成的。
![]()
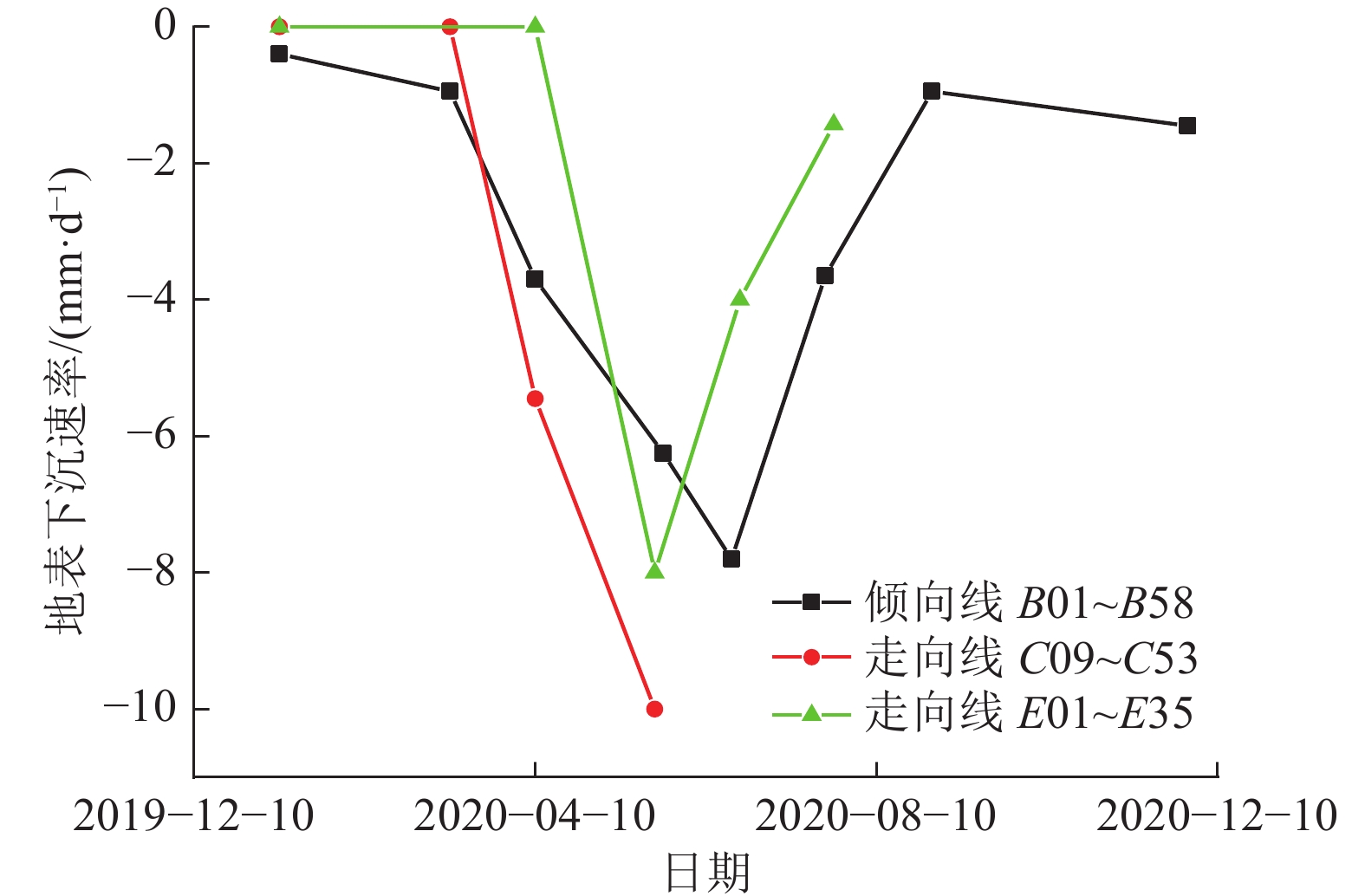
图 11 2202工作面走向线E1～E35测点地表下沉统计Figure 11. Statistical of surface subsidence at measuring points E1～E35 of strike line of panal 2202 working face图13为2202工作面的地表下沉速度曲线。由图13分析可知，B、C、E测线下沉状态可以分为3个阶段。2020年3月之前，工作面推进距小于550 m，地表下沉速度0～1.5 mm/d，为缓慢下沉阶段；2020年03月至2020年08月地表下沉速度1.5～10 mm/d，为急剧下沉阶段；2020年8月以后，下沉速度0～1.67 mm/d，为稳定阶段。2020年5月上旬至2020年6月下旬，地表下沉速率保持在7 mm/d以上，下沉速率最大值分别为9.87、7.97、7.67 mm/d，最大下沉速度出现在采空区中部，此时工作面距开切眼879～960 m，这与理论分析得到的高位厚硬岩层“O-X”破断区域相近。
综合分析图10—图13可知：①2020年3月之前，工作面推进距小于550 m ，由于采空区面积有限，覆岩破坏尚未完全波及厚硬岩层，因而地表下沉量较小。②从2020年3月开始，逐渐进入双见方阶段，2201、2202两工作面采空区贯通，形成大范围采空区，覆岩破坏高度发展至厚硬岩层，悬顶面积快速增大，在自重及其上覆岩层重力作用下发生弯曲下沉，此阶段地表下沉速度持续变大。③2020年6月8日厚硬岩层悬顶距达到极限破断距，发生破断回转下沉，沉降速度猛然增至最大，此时工作面推进距离约为960 m，与理论分析确定的高位岩层破断步距982 m较为接近，从而侧面证明了本文理论模型及其解算的正确性。
5.2 微震响应规律分析
营盘壕煤矿采用微震监测系统实时监测全矿微震信号，对2017年3月至2021年6月期间2201、2202工作面微震频次、释放能量变化规律与岩层破断关系进行分析。2201工作面回采期间，主要以小能量微震事件为主，102～103 J区间的矿震频次最多，占总频次的55.06%；105 J以上的微震事件，仅占总频次的0.77%；该阶段微震事件主要是关键层1、关键层2破断运动造成的。
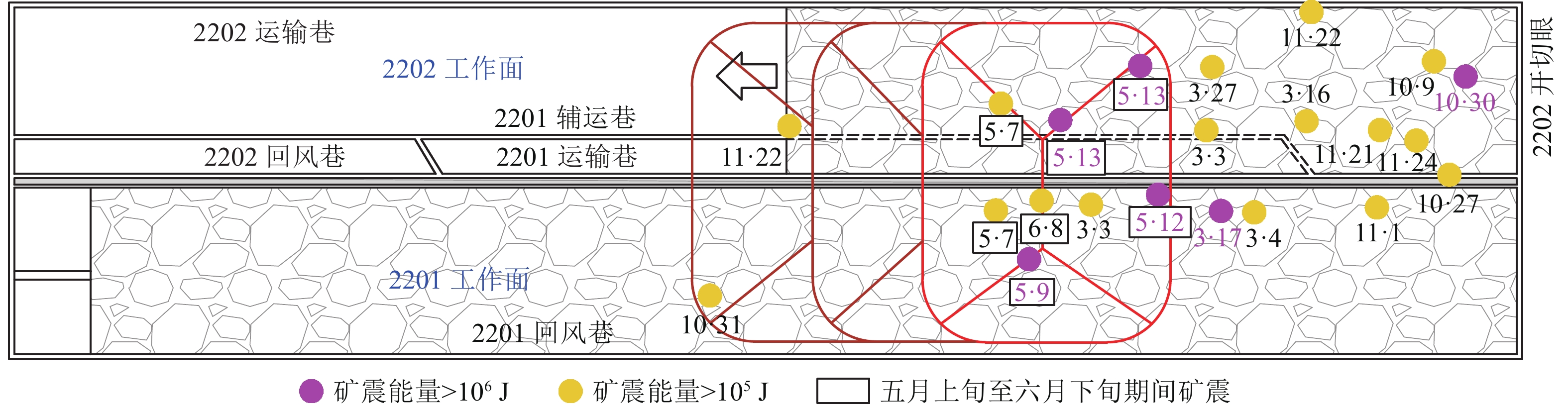
2202工作面回采期间，大能量事件显著增多，105 J以上矿震共发生21次（图14），多发生在2202工作面后方100 m范围内及2201采空区范围内，由此可知，2202工作面大能量矿震主要是采空区后方顶板岩层破断引起的。特别地，2020年5月上旬至2020年6月下旬期间共发生1×105 J以上微震事件7次（“5·7”“5·7”“5·9”“5·12”“5·13”“5·13”“6·8”），其中106 J以上微震事件5次，占比开采以来106 J以上微震事件总量的71.4%；这是由于该时间段内，工作面正由距开切眼879 m推进至960 m过程中，厚硬岩层正处于悬顶→“O-X”破断过渡期间，厚硬岩层不断产生裂隙诱发大能量事件。结合地表沉陷规律可知，该阶段内地表沉降速率均保持在7 mm/d以上；当工作面推进至960 m时发生“6·8”矿震事件，能量达到历史最大值4.93×106 J，此时地表下沉速率亦达到最大值。从强矿震发生平面位置上看，强矿震发生在“O-X”破断区域，与地表沉降最大值区域重合度较高，从发生剖面位置上看，强矿震发生在距离煤层300～400 m范围内。
![]()
图 14 2022工作面推采期间大能量矿震事件发生位置Figure 14. Location of mine earthquakes with large eneries during panel 2022 retreating根据文中地表沉陷与微震响应时序特征，结合相邻矿井白垩系内岩层移动监测结果[23]，可以推知，白垩系内部厚硬岩层破断运动是地表沉陷和大能量事件频发的主要原因。
6. 结 论
1）针对陕蒙地区白垩系岩层距煤层远、厚度大、整体性好的特殊赋存条件，建立了远场高位厚硬岩层破断力学模型，采用符拉索夫厚板理论解算出了高位厚硬岩层初次破断临界力学判据，重点分析了厚硬岩层破断规律与岩石抗拉强度、厚度、倾向悬露长度的关联性。
2）营盘壕煤矿2201工作面推采过程中，白垩系砂岩组不会发生破断；当2202工作面推采至960 m左右时，厚硬岩层发生竖向“O-X”破断；随着工作面继续推进188 m，厚硬岩层将会发生周期性破断。
3）2201工作面推采期间地表沉降值整体较小且无较大变化；2202工作面期间地表下沉依次经历缓慢下沉阶段、急剧下沉阶段、稳定阶段，地表下沉速度在距开切眼960 m处达到最大，最大值沉降速率为9.87 mm/d。
4）2201工作面回采期间，主要以102～103 J小能量微震事件为主，主要是低位岩层破断运动造成的；2202工作面回采期间，强矿震主要是采空区后方顶板岩层破断引起的，矿震发生位置处于“O-X”破断区域，与地表沉降最大值区域重合度较高，验证了文中理论分析的正确性。
-
![]()
图 3 远场高位厚硬岩层厚板力学模型
Figure 3. Thick-plate mechanical model of super-high position hard-and-hick strata
![]()
图 4 岩层破断尺寸（a、b）与岩层抗拉强度σmax关系变化
Figure 4. Fracture size (a, b) and tensile strength of rock stratum σmax relation change
![]()
图 5 岩石抗拉强度σs与走向悬露长度a关系
Figure 5. Relationship between rock tensile strength σs and strike overhang length a
![]()
图 6 岩层厚度h与走向悬露长度a关系
Figure 6. Relation between thickness of strata h and strike overhang length a
![]()
图 7 倾向悬露长度b与走向悬露长度a关系
Figure 7. Relation between inclination overhang length b and strike overhang length a
![]()
图 8 高位厚硬岩层破断力学过程
Figure 8. Fracture mechanics process of high position hard-and-hick strata
![]()
图 10 2202工作面倾向线B1～B58测点地表下沉统计
Figure 10. Statistical of surface subsidence at monitoring points B1～B58 of inclination line of panal 2202
![]()
图 12 2202工作面走向线C9～C53测点地表下沉统计
Figure 12. Statistical of surface subsidence at measuring points C9～C53 of strike line of panal 2202 face
![]()
图 11 2202工作面走向线E1～E35测点地表下沉统计
Figure 11. Statistical of surface subsidence at measuring points E1～E35 of strike line of panal 2202 working face
-
[1] 赵善坤,赵 阳,王 寅,等. 采动巷道侧向高低位厚硬顶板破断模式试验研究[J]. 煤炭科学技术,2021,49(4):111−120. ZHAO Shankun,ZHAO Yang,WANG Yin,et al. Experimental study on fracture mode of lateral high and low thickand hard roof in mining roadway[J]. Coal Science and Technology,2021,49(4):111−120.
[2] 郑上上,孔德中. 工作面坚硬顶板破断特征与覆岩运移规律[J]. 煤矿安全,2019,50(5):257−262. ZHENG Shangshang,KONG Dezhong. Fracture characteristics of hard roof and overlying rock movement in working face[J]. Safety in Coal Mines,2019,50(5):257−262.
[3] 于 斌,高 瑞,夏彬伟,等. 大空间坚硬顶板地面压裂技术与应用[J]. 煤炭学报,2021,46(3):800−811. YU Bin,GAO Rui,XIA Binwei,et al. Ground fracturing technology and application of hard roof in large space[J]. Journal of China Coal Society,2021,46(3):800−811.
[4] 荣 海,于世棋,王雅迪,等. 坚硬覆岩的结构失稳运动规律及其对冲击地压的影响[J]. 采矿与岩层控制工程学报,2022,4(6):16−26. RONG Hai,YU Shiqi,WANG Yadi,et al. Analysis of structural instability movement of hard overburden and its influence mechanism on rockburst[J]. Journal of Mining and Strata Control Engineering,2022,4(6):16−26.
[5] 杜涛涛,鞠文君,陈建强,等. 坚硬顶板遗留煤层下综放工作面冲击地压发生机理[J]. 采矿与安全工程学报,2021,38(6):1144−1151. DU Taotao,JU Wenjun,CHEN Jianqiang,et al. Mechanism of rock burst in fully mechanized caving faces under residual coal seams with hard roof[J]. Journal of Mining & Safety Engineering,2021,38(6):1144−1151.
[6] 窦林名,田鑫元,曹安业,等. 我国煤矿冲击地压防治现状与难题[J]. 煤炭学报,2022,47(1):152−171. doi: 10.13225/j.cnki.jccs.yg21.1873 DOU Linming,TIAN Xinyuan,CAO Anye,et al. Present situation and problems of coal mine rock burst prevention and control in China[J]. Journal of China Coal Society,2022,47(1):152−171. doi: 10.13225/j.cnki.jccs.yg21.1873
[7] 翟明华,姜福兴,朱斯陶,等. 巨厚坚硬岩层下基于防冲的开采设计研究与应用[J]. 煤炭学报,2019,44(6):1707−1715. ZHAI Minghua,JIANG Fuxing,ZHU Sitao,et al. Research and application of mining design based on prevention of rock burst under giant thickness hard strata[J]. Journal of China Coal Society,2019,44(6):1707−1715.
[8] 蒋金泉,张培鹏,聂礼生,等. 高位硬厚岩层破断规律及其动力响应分析[J]. 岩石力学与工程学报,2014,33(7):1366−1374. JIANG Jinquan,ZHANG Peipeng,NIE Lisheng,et al. Fracturing and dynamic response of high and thickstratas of hard rocks[J]. Chinese Journal of Rock Mechanics and Engineering,2014,33(7):1366−1374.
[9] 姜福兴,刘 懿,张益超,等. 采场覆岩的“载荷三带”结构模型及其在防冲领域的应用[J]. 岩石力学与工程学报,2016,35(12):2398−2408. JIANG Fuxing,LIU Yi,ZHANG Yichao,et al. A three-zone structure loading model of overlying strata and its application on rockburst prevention[J]. Chinese Journal of Rock Mechanics and Engineering,2016,35(12):2398−2408.
[10] 朱卫兵,于 斌,鞠金峰,等. 采场顶板关键层横“U-Y”型周期破断特征的试验研究[J]. 煤炭科学技术,2020,48(2):36−43. ZHU Weibing,YU Bin,JU Jinfeng,et al. Experimental study on horizontal “U-Y” periodical breakage characteristics of key strata in stope roof[J]. Coal Science and Technology,2020,48(2):36−43.
[11] 张 明,姜福兴,李克庆,等. 基于厚硬关键层破断的地面震动损害边界研究[J]. 中国矿业大学学报,2017,46(3):514−520, 536. ZHANG Ming,JIANG Fuxing,LI Keqing,et al. A study of surface seismic damage boundary based on the break and movement of extremely thick key stratum[J]. Journal of China University of Mining & Technology,2017,46(3):514−520, 536.
[12] 张 明,姜福兴,陈广尧,等. 基于厚硬岩层运动状态的采场应力转移模型及其应用[J]. 岩石力学与工程学报,2020,39(7):1396−1407. ZHANG Ming,JIANG Fuxing,CHEN Guangyao,et al. A stope stress transfer model based on the motion state of thick and hard rock strata and its application[J]. Chinese Journal of Rock Mechanics and Engineering,2020,39(7):1396−1407.
[13] 张 明,成云海,王 磊,等. 浅埋复采工作面厚硬岩层–煤柱结构模型及其稳定性研究[J]. 岩石力学与工程学报,2019,38(1):87−100. ZHANG Ming,CHENG Yunhai,WANG Lei,et al. Structure model and stability research of thick hard strata-coal pillar in shallow-buried re-mined panels[J]. Chinese Journal of Rock Mechanics and Engineering,2019,38(1):87−100.
[14] 王树立,张开智,蒋金泉,等. 超厚高位红层砂岩破断运动与矿震活动规律[J]. 采矿与安全工程学报,2016,33(6):11161122. WANG Shuli,ZHANG Kaizhi,JIANG Jinquan,et al. The fracture and rockburst laws of high-position hard and extremely thick red beds[J]. Journal of Mining & Safety Engineering,2016,33(6):11161122.
[15] 刘一扬,宋选民,王仲伦. 厚硬岩层周期破断步距计算及影响因素分析[J]. 煤炭工程,2020,52(7):106−111. LIU Yiyang,SONG Xuanmin,WANG Zhonglun. Calculation of periodical fracture interval and analysis of influencing factors in thick and hard rock strata[J]. Coal Engineering,2020,52(7):106−111.
[16] 赵 通,刘长友,弓培林. 近距离巨厚坚硬岩层破断结构及分区控制[J]. 采矿与安全工程学报,2019,36(4):719−727. ZHAO Tong,LIU Changyou,GONG Peilin. Roof fractured structure and zonal control of super thick and hard close rock[J]. Journal of Mining & Safety Engineering,2019,36(4):719−727.
[17] 张广超, 陶广哲, 孟祥军, 等. 巨厚松散层下软弱覆岩破坏规律研究[J], 煤炭学报, 2022, 47(11): 3572−3598. ZHANG Guangchao, TAO Guangzhe, MENG Xiangjun, et al. Failure law of weak overburden stratum underlying extra-thick alluvium[J]. Journal of China Coal Society, 2022, 47(11): 3572−3598.
[18] 何福保, 沈亚鹏. 板壳理论[M]. 西安: 西安交通大学出版社, 1993: 160−189. [19] 钱鸣高, 缪协兴, 许家林, 等. 岩层控制的关键层理论[M]. 徐州: 中国矿业大学出版社, 2003: 2-6. [20] 黄正均,任奋华,李 远,等. 不同试验方法下岩石抗拉强度及破裂特性[J]. 实验技术与管理,2020,37(10):45−49. HUANG Zhengjun,REN Fenhua,LI Yuan,et al. Tensile strength and damage characteristics of rock under different test methods[J]. Experimental Technology and Management,2020,37(10):45−49.
[21] 杨烜宇. 不同强度准则对预测岩石抗拉强度的适用性[J]. 山西交通科技,2022(276):42−46, 50. YANG Xuanyu. Applicability of different strength criteria forforecasting tensile strength of rocks[J]. Shanxi Science & Technology of Transportation,2022(276):42−46, 50.
[22] 姜福兴,杨淑华,XUN Luo. 微地震监测揭示的采场围岩空间破裂形态[J]. 煤炭学报,2003,28(4):357−360. JIANG Fuxing,YANG Shuhua,XUN Luo. Spatial fracturing progresses of surrounding rock masses in longwall face monitored by microseismic monitoring techniques[J]. Journal of China Coal Society,2003,28(4):357−360.
[23] 白贤栖, 曹安业, 杨 耀, 等. 高位巨厚覆岩运移规律及矿震触发机制研究[J]. 煤炭科学技术, 2023, 51(3): 10−20. BAI XiangQI, CAO Anye, YANG yao, et al. Study on movement law of extremely thick strata and triggering mechanism of mine earthquakes[J]. Coal Science and Technology, 2023, 51(3): 10−20.
-
期刊类型引用(11)
1. 杨伟利，韩恩魁，娄智帅. 不对称综采面上覆巨厚砾岩破断及矿压规律研究. 中原工学院学报. 2025(01): 64-72 . 
百度学术
2. 李怀展，孙兢超，郭广礼，唐超，郑辉，张连贵，孟凡贞. 巨厚弱胶结覆岩导水裂隙带演化特征及发育高度预测方法. 煤炭科学技术. 2025(02): 289-300 . 本站查看
3. 张敏剑. 基于厚硬顶板沿空留巷下的切顶卸压参数研究. 煤矿现代化. 2025(04): 65-69+74 . 百度学术
4. 许斌，张沿，徐维正. 巨厚坚硬岩层运移对采场超前支承压力影响实验研究. 煤炭工程. 2024(01): 134-140 . 百度学术
5. 张广超，张广有，周广磊，张照允，吕凯，尹茂胜，闫宪洋，李振国. 多工作面连续开采地表沉陷与强矿震联动响应规律. 采矿与岩层控制工程学报. 2024(01): 117-130 . 百度学术
6. 左昊，张广有，周泽森，李仕宾，曲治. 厚硬顶板直覆型沿空巷道冲击失稳机理及防治研究. 矿业研究与开发. 2024(06): 205-216 . 百度学术
7. 曹东京，刘国磊，梁文昭，郝喜庆，田利华，薛建军. 高位巨厚砾岩对工作面开采地表沉降控制机理. 煤矿安全. 2024(06): 141-150 . 百度学术
8. 张广超，尹茂胜，周广磊，陶广哲，张照允，闫宪洋，李振国，吕凯. 厚硬岩层下板结构破断应力-能量场积聚演化规律. 中国矿业大学学报. 2024(04): 647-663 . 百度学术
9. 李少华. 工作面开采地表变形观测及影响规律分析. 山西煤炭. 2024(03): 140-148 . 百度学术
10. 李怀展，唐超，郭广礼，陈福，李伟，周华安，黄建勇. 热力耦合作用下煤炭地下气化地表沉陷预测方法. 煤炭科学技术. 2023(10): 242-251 . 本站查看
11. 胡全宏，庞立宁，冯涛，曹宪海. 深埋厚顶板工作面高应力强动载矿压显现机理研究. 煤炭工程. 2023(S1): 124-130 . 百度学术
其他类型引用(6)
下载:
计量
- 文章访问数: 133
- HTML全文浏览量: 34
- PDF下载量: 88
- 被引次数: 17
